＊图与补图孤立断裂度的关系

王世英，王牟江山，冯凯，林上为，张明瑜

（1.山西大学 数学科学学院，山西 太原 030006；2.中国科学院 研究生院，北京 100049；3.山西大学 计算机与信息技术学院，山西 太原 030006）

＊图与补图孤立断裂度的关系

王世英1，王牟江山2，冯凯3，林上为1，张明瑜1

（1.山西大学 数学科学学院，山西 太原 030006；2.中国科学院 研究生院，北京 100049；3.山西大学 计算机与信息技术学院，山西 太原 030006）

连通图G的孤立断裂度isc（G）＝max｛i（G－S）－｜S｜∶S∈C（G）｝，其中i（G－S）是G－S中的孤立点数，C（G）是G的点割集.文章研究了图与补图孤立断裂度的关系.

网络；可靠性；孤立断裂度

0 引言

本文仅考虑简单图.设图G＝（V（G），E（G）），其中V（G）和E（G）分别为图G的顶点集和边集.若｜V（G）｜＝1，则称G为平凡图.设S⊂V（G）.当G是完全图时，若G－S是平凡图，称S是G的一个点割；当G是非完全连通图时，若G－S是不连通的，则称S是G的一个点割；G的连通度κ（G）为G的一个最小点割的顶点数.G的点割集C（G）＝｛S∶S是G的一个点割｝.G的分支数，奇分支数和孤立顶点数分别用ω（G），ω0（G）和i（G）表示.G的亏度def（G）是指G中未被G的一个最大匹配饱和的顶点数.下面是匹配理论中著名的 Tutte定理［1］.

定理1（Tutte定理［1］） 一个图G有完美匹配当且仅当对所有的S⊆V（G），有ω0（G－S）≤｜S｜成立.

1958年，Berge在Tutte定理的基础上给出了图G的一个最大匹配的精确刻画.特别的，他证明了def（G）＝max｛ω0（G－S）－｜S｜∶S⊆V（G）｝.此后，亏度这一参数得到许多学者的关注［2－5］.下面给出另一个著名的定理.

定理2［1］设S为哈密顿图G的一个顶点集合.则ω（G－S）≤｜S｜.

受该定理的启发，Jung［6］引进断裂度这一新概念来对图的哈密顿性进行讨论.

定义1［6］设G为一个连通图.图G的断裂度sc（G）＝max｛ω（G－S）－｜S｜∶S∈C（G）｝.

断裂度源于分数因子理论，近年来，它被普遍认为是度量图的可靠性的有效参数之一［7－11］.分数因子理论［12－13］被广泛应用在网络设计，组合拓扑和决策链等很多领域.一个分数1－因子是指一个为图G的每条边指派一个区间［0，1］上分数的函数h，使得对每个顶点x有 ∑e∈Ex h（e）＝1成立，其中Ex＝｛e∶e＝xy∈E（G）｝.下面给出具有分数1－因子图的一个刻画.

定理3［12］一个图G有分数1－因子当且仅当对任何S⊆V（G）有i（G－S）≤｜S｜成立.

受定理3的启发，王世英等在文［14］中引进孤立断裂度这一新概念对图的稳定性进行讨论.

定义2［14］设G是一个连通图.图G的孤立断裂度isc（G）＝max｛i（G－S）－｜S｜∶S∈C（G）｝.

设S＊是图G的一个点割，若i（G－S＊）－｜S＊｜＝isc（G），则称S＊为一个孤立断裂度集.

一个处理器互连网络或通讯网络通常用一个图G＝（V，E）来表示，其中V中每个顶点对应一个处理器或一个通讯器件，E中每条边对应一对处理器或一对通讯器件之间的一条直接通讯线路.在设计这些网络时，可靠性是一个非常重要的因素［15］.由于孤立顶点同其他顶点无法通讯联系，所以我们期望故障网络具有尽可能少的孤立顶点.对G的一个点割S，从G中移除S的难度可以用｜S｜来度量，由S的移除带来的彻底毁坏程度可用i（G－S）来度量.因此，孤立断裂度是一个合理、合适的网络可靠性参数.本文对图与补图孤立断裂度的关系进行研究.下面我们介绍将用到一些基本概念和术语.

V（G）的一个子集S被称为一个独立集若S中任意两个顶点在G中都不相邻.G的最大独立集的顶点数称为G的独立数，记为α（G）.V（G）的一个子集K使得G中每条边至少有一个端点在K中被称为G的一个覆盖.G的最小覆盖的顶点数称为G的覆盖数，记为β（G）.设X是V（G）的一个非空子集.G的由X导出的子图记为G［X］.G［V（G）－X］简记为G－X.若X＝｛v｝，则G－｛v｝简记为G－v.其它未给出的定义参见［1］.

1 图与补图孤立断裂度的关系

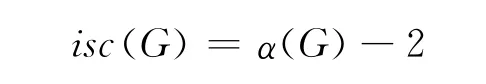
和

设G的顶点集V（G）为｛v1，v2，…，vn｝且不失一般性，设U＝｛v1，v2，…，vα（G）｝是G的一个最大独立集.

若i（G－S＊）＝3，｜S＊｜＝2，设S＊＝｛x1，x2｝，点x3、x4和x5为G－S＊中的孤立点.注意到｛x3，x4，x5｝中必有一个点在G［U2］中.又由于G［U2］是完全图，而｛x3，x4，x5｝是孤立点集，故｛x3，x4，x5｝中恰有一个点在G［U2］中.因此，不妨设为x3∈U2且｛x4，x5｝＝｛v1，v2｝.注意到G［U2］是G中的（n－2）团，故若V（G）＼（S＊∪｛x3，x4，x5｝）中还存在其它的点x＊，则x＊与x3在G－S＊中必相邻，这与x3为G－S＊中的孤立点矛盾.因此，n＝5.这时x3＝v3.否则不妨设x3＝v4，这时｛x1，x2｝＝｛v3，v5｝.不妨设x1＝v3，x2＝v5，由于｛v1，v2，v3｝是G的独立集，故v5与v1，v2均相邻.由于｛v3，v4，v5｝＝U2，故G［U2］是一个完全图.因此，d G（v5）＝4，即d¯G（v5）＝0，矛盾.这时｛x1，x2｝＝｛v4，v5｝.此时G［｛v3，v4，v5｝］是完全图，G［｛v1，v2，v3｝］是空图且v1与｛v4，v5｝中至少一点相邻，v2与｛v4，v5｝中至少一点相邻.若v1，v2都与v4相邻，则在¯G中v4是孤立点，矛盾.同理，v1，v2不能都与v5相邻.因此，不失一般性可设v1只与v4相邻，v2只与v5相邻，这说明G≅G5.证毕.

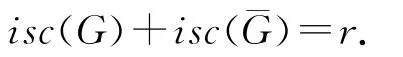
以下两个引理的结果是显然的故未给出证明.

2 互补的哈密顿图的孤立断裂度的关系

引理10［1］一个简单图是哈密顿图当且仅当它的闭包是哈密顿图.

引理11 若G是哈密顿图，则G的孤立断裂度isc（G）≤0.

证明 设S＊是G的孤立断裂度集.由定理2，有ω（G－S＊）≤｜S＊｜.因为i（G－S＊）≤ω（G－S＊），所以isc（G）＝i（G－S＊）－｜S＊｜≤ω（G－S＊）－｜S＊｜≤0.证毕.

由引理10容易得到下面的引理.

引理12 对任意给定的正整数n（≥8）和k（1≤k≤n－7），构造n阶图H如下：V（H）＝｛v1，v2，…，vn｝，E（H）＝E（Kn）＼（E1∪E2），其中E1＝｛viv i＋1∶i＝1，2，…，n，1＋i是模n加法｝，E2＝｛v1vi∶i＝3，…，k＋2｝.则

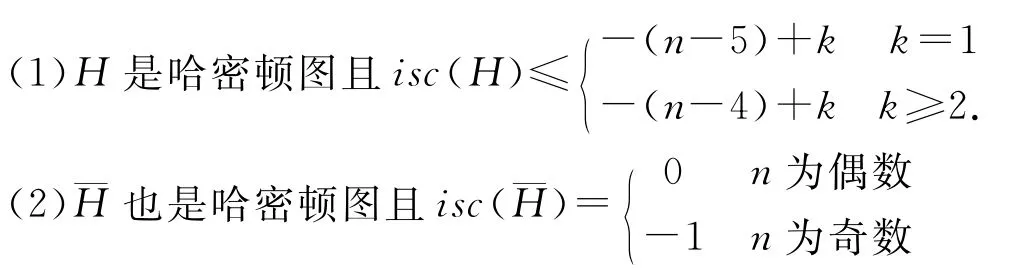
证明 由引理11可得isc（H）＋isc（）≤0.由定理5有isc（H）＋isc（）≥－（n－3）.证毕.

定理9 设n（≥8）和r为两个给定的正整数使得－（n－6）≤r≤－4.那么存在n阶互补的哈密顿图H和，使得isc（H）＋isc）＝r.

证明 当n为偶数时，由引理12知存在n阶互补的哈密顿图H和，使得isc（H）＋isc（）是｛－（n－6），…，－4，－3｝中任意一个数.当n为奇数时，由引理12知存在n阶互补的哈密顿图H和¯H，使得isc（H）＋isc（¯H）是｛－（n－5），－（n－6），…，－4｝中任意一个数.综上得证.

［1］ Bondy J A，Murty U S R.Graph Theory［M］.New York：Springer，2007.

［2］ Bauer D，Broersma H J，Morgana A，etal.Tutte Sets in Graphs I：maximal Tutte sets and D－graphs［J］.JournalofGraph Theory，2007，55（4）：343－358.

［3］ Bauer D，Broersma H J，Kahl N，etal.Tutte Sets in Graphs II：The Complexity of Finding Maximum Tutte Sets［J］.DiscreteAppliedMathematics，2007，155（15）：1336－1343.

［4］ Busch A，Ferrara M，Kahl N.Generalizing D－graphs［J］.DiscreteAppliedMathematics，2007，155（18）：2487－2495.

［5］ Traldi L.Parallel Connections and Coloured Tutte Polynomials［J］.DiscreteMathematics，2005，290（2－3）：291－299.

［6］ Jung H A.On a Class of Posets and the Corresponding Comparability Graphs［J］.JournalofCombinatorialTheorySeriesB，1978，24（2）：125－133.

［7］ Giakoumakis V，Roussel F，Thuillier H.Scattering Number and Modular Decomposition［J］.DiscreteMathematics，1997，165－166（15）：321－342.

［8］ Kirlangic A.A Measure of Graph Vulnerability：Scattering Number［J］.InternationalJournalofMathematicsandMathematicalSciences，2002，30（1）：1－8.

［9］ Li F W，Li X L.The Neighbour－scattering Number can Be Computed in Polynomial time for Interval Graphs［J］.ComputersandMathematicswithApplications，2007，54（5）：679－686.

［10］ Kratsch D，Kloks T，Müller H.Measuring the Vulnerability for Classes of Intersection Graphs［J］.DiscreteApplied Mathematics，1997，77（3）：259－270.

［11］ Zhang S G，Wang Z G.Scattering Number in Graphs［J］.Networks，2001，37（2）：102－106.

［12］ Edward R，Scheinerman E，Ullman D H.Fractional Graph Theory：A Rational Approach to the Theory of Graphs［M］.New York：John Wiley and Sons Inc，1997.

［13］ Liu Y，Liu G Z.The Fractional Matching Numbers of Graphs［J］.Networks，2002，40（4）：228－231.

［14］ 王世英，杨玉星，林上为，等.图的孤立断裂度［J］.数学学报，2011，54（5）：861－874.

［15］ Bermond J C，Homobono N，Peyrat C.Large Fault－tolerant Interconnection Networks［J］.GraphsandCombinatorics，1989，5（1）：107－123.

［16］ 王世英，张东艳.图与补图断裂度的关系［J］.晋中师专学报，1991，1：37－41.

［17］ Chartrand G，Schuster S.On the Independence Number of Complementary graphs［J］.TransactionsoftheNewYorkA－cademyofScienceⅡ，1974，36（3）：247－281.

Relation of the Isolated Scatting Number of a Graph and Its Complement Graph

WANG Shi－ying1，WANGMU Jiang－shan2，FENG Kai3，LIN Shang－wei1，ZHANG Ming－yu1
（1.SchoolofMathematicalScience，ShanxiUniversity，Taiyuan030006，China；2.GraduateUniversityofChineseAcademyofSciences，Beijing100049，China；3.SchoolofComputerScienceandTechnology，ShanxiUniversity，Taiyuan030006，China）

The isolated scattering numberisc（G）＝max｛i（G－S）－｜S｜：S∈C（G）｝，whereGis a connected graph，i（G－S）is the number of isolated vertices ofG－SandC（G）is the set of vertex cuts ofG.In this paper，we investigate the relation of the isolated scatting number of a graph and its complement graph.

networks；vulnerability；isolated scattering number

O157.5

A

0253－2395（2012）02－0206－05＊

2011－09－27

国家自然科学基金（61070229）；教育部博士点基金（博导类）（20111401110005）

王世英（1961－），男，山西晋中人，博士，教授，主要研究领域为图论和DNA计算.