空间飞行器远尾区诱发场的调制不稳定性

廖晶晶，王苏敏，李艳玲

（江西理工大学，a.应用科学学院；b.信息工程学院，江西赣州341000）

空间飞行器远尾区诱发场的调制不稳定性

廖晶晶a，王苏敏a，李艳玲b

（江西理工大学，a.应用科学学院；b.信息工程学院，江西赣州341000）

空间飞行器穿过电离层时，其远尾区与等离子体发生的非稳态相互作用可以通过一组高频场和密度扰动的非线性耦合方程来描述.从该组方程出发，通过线性分析得到扰动的色散方程.理论分析和数值计算表明，飞行器远尾区诱发场是调制不稳定的，它将会坍塌成小尺度的局域结构，并形成密度空穴，这为隐形飞行器的探测提供理论依据；诱发场的特征尺度与最大增长率不仅依赖于泵波振幅与扰动波矢量之间的夹角，同时也受到泵波能量密度的影响.

飞行器；调制不稳定；密度空穴；坍塌

0 引言

隐身飞行器可以通过改进外形设计和涂上具有吸收雷达波的材料，来消除雷达对它的探测，但却无法消除飞行器与等离子体之间的相互作用，即无法消除由飞行器的飞行而带来的运动效应[1].当飞行器穿越电离层时，由于空间飞行器与周围等离子体之间复杂的相互作用会激发起各种等离子波以及不稳定性.特别是当飞行器的天线系统辐射出大量的高频电磁波时，这种电磁波与周围等离子体发生相互作用，非线性效应会导致波的强度陡增，进而形成电磁孤波[2].事实上，当阿波罗飞船发射时，它在电离层激起了一种大振幅孤波[3].反过来，场的变化又将引起带电粒子密度的变化，而被雷达所探测.因此，如果人们能够很好地了解并掌握这些场和密度的变化情况，就可以得知飞行器的运动情况；尽管飞行器可能具有雷达波探测不到的隐身特点，但这种由飞行器运动引起的场和带电粒子密度的变化以及它们所具有的特征是无法消除，这就使得人们可以通过探测场和带电粒子密度的变化来发现隐身飞行器，这在国防上占有重要的地位[4].

近年来，人们对这种相互作用产生的各种效应进行了大量的理论[1,5-6]和实验研究[7-8].早期理论的缺点在于人们对该理论中的非静态问题认识不足[5].但很显然，飞行器周围激发起来的等离子体与不稳定性均属于非静态问题，这是必须克服的困难之一.众所周知，飞行器的特征尺度一般为米的量级，在电离层中，远小于粒子的平均自由程；换句话说，我们不能把近体空间看成为碰撞频繁的连续介质，而采用动力学理论来描述飞行器周围区域的粒子分布是必要的[7].另一方面，由于飞行器速度υ0具有典型的中介速度，即υTi＜＜υ0＜＜υTe（这里υTi和υTe分别是离子和电子的热速度），在此条件下，飞行器对处于运动平衡的电子影响甚微，电子的动力学效应可以不计.这种情况下，我们可以利用流体近似来描述电子，同时，离子的分布函数应该服从伏拉索夫方程.此外，在远离飞行器的远尾区，准中性条件总是合适的：这里运动动且在许多电离层动力学问题中，地磁效应几乎可略去不计[4].

考虑到以上情况，Li[2]理论推导得到了描述飞行器远尾区诱发场动力学行为的非稳态非线性控制方程.2003年，胡等人[9]对该组方程进行了数值计算，结果表明，诱发场由于调制不稳定性将坍塌形成小尺度的局域结构，但他们计算过程中选取了特殊的初始湍动场.为了弄清诱发场是否稳定，我们有必要研究非线性控制方程在Lyapunov意义上的有限调制振幅单色泵波的稳定性.文章从非线性控制方程出发，通过线性分析得到了扰动的色散关系.用解析方法讨论两种特殊条件下调制不稳定性的增长率，并采用数值方法研究一般情况下不同角度的调制不稳定性.

1 非线性控制方程及横扰动的线性分析

利用流体近似描述电子，同时考虑离子的分布函数服从伏拉索夫方程[2,9]，描述飞行器远尾区诱发场的无量纲的非线性控制方程为：

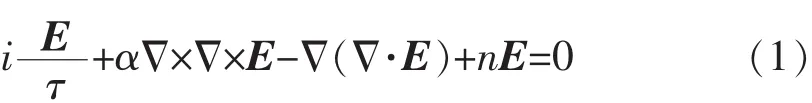
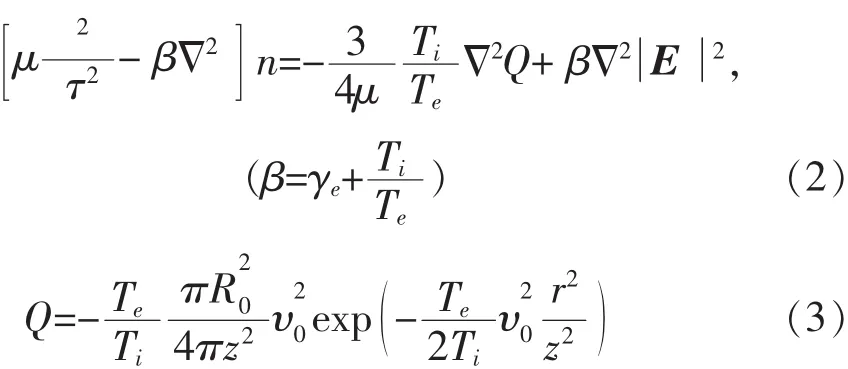
无量纲变化为，

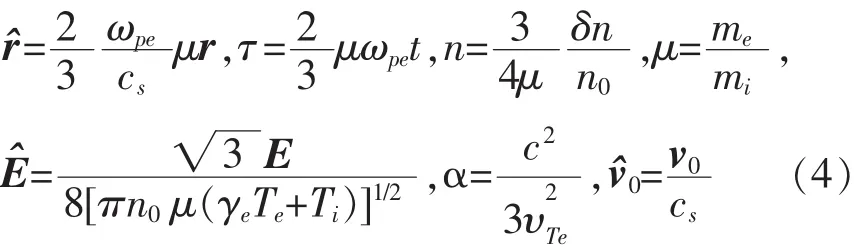
其中，E是电场，n是扰动密度，ωpe是电子等离子体频率，cs是离子声速，υTe电子热速度，γe=5/3是电子比热比，Ti和Te分别是离子和电子温度，其它符号具有通常物理意义[10].

在远尾区，如果飞行器上的辐射天线是强辐射源的话，作为第一级近似[2,11]，我Δ们可以略去方程（2）右边第一项，即方程中正比于2Q的项，那么，方程（2）可以写成

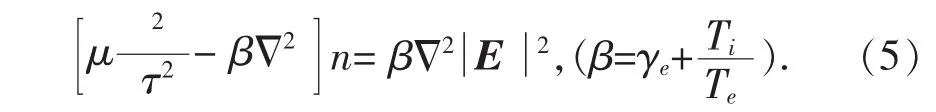
现在我们来研究在第一级近似下有限振幅等离子体波所诱发的不稳定性问题.首先我们简单讨论调制不稳定性产生的物理机制.假设等离激元有稳定的能量输入，当等离子体中大振幅电子振荡相当强烈时，它所产生的有质动力就显得非常重要，平衡时能与等离子体热压力相抗衡（无外磁场的情况下）[2].如果发生一种使等离子体密度局部稀化的扰动，那么热压降低，同时朗缪尔频率也降低，根据射线方程，朗缪尔波朝着等离子体频率降低的方向折射进入此局部区域，因而密度稀化区捕获更强的朗缪尔波；波的有质动力与等离子体热压力不能抗衡，使等离子体更迅速地从此区域排出，引起密度进一步稀化.显然，这里就开始出现不稳定性，这就是所谓李雅普洛夫(Lyapunov)意义上不稳定[11].

可以证明，如下形式的平面波是方程（1）和（5）的解，假设其中

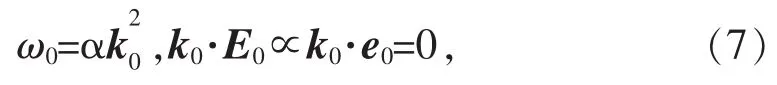
其中，E0是来自飞行器上辐射天线的泵波振幅；这里e0=E0/E0是单位矢量，并满

对于小扰动EII，nII，线性化方程（1）的复共轭方程和（5），得到

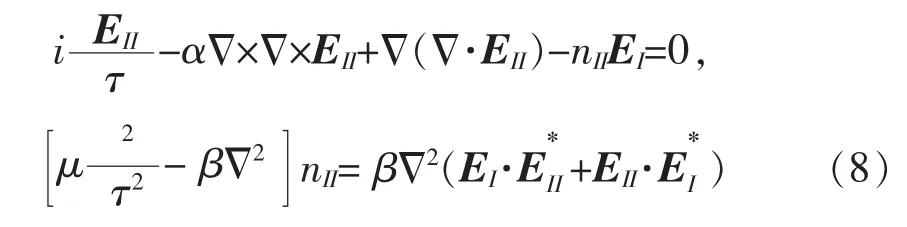
考虑如下扰动形式：

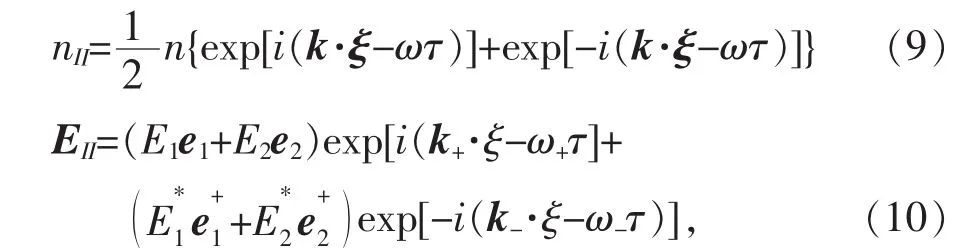
其中

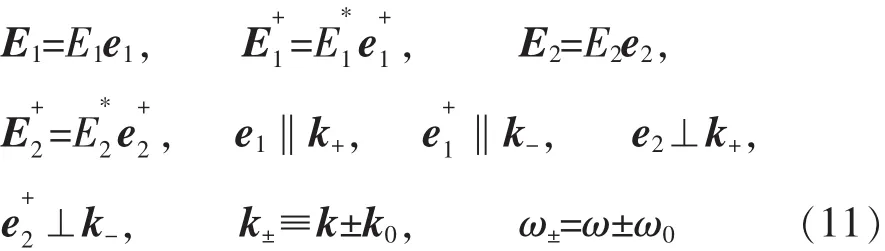
这里e1，e2，，是实单位矢量.将方程(6)、(10)以及方程(11)代入方程(9)中得到

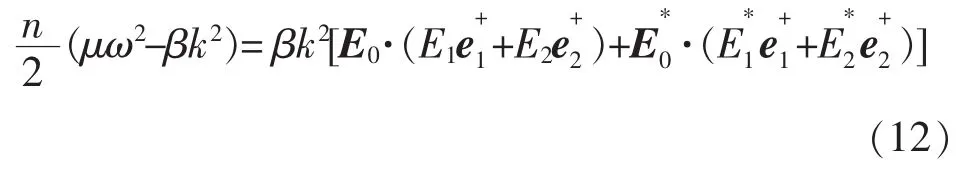
同样的，从方程(8)可以得到

从方程(14)容易得到

同样地，从方程(15)得到

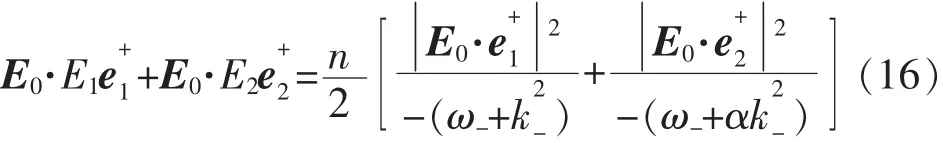
将方程(16)、(17)代入(13)中得到如下色散方程：

这里θ+是E0与e1之间的夹角，θ-是E0与之间的夹角.

我们首先考虑一种简单的情况，假设k0‖k,亦即θ±=π/2,色散方程(18)可以写为

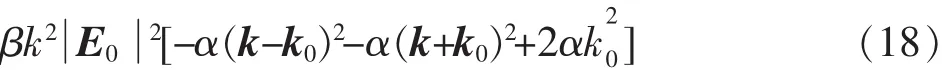
对于飞行器远尾区，k＞＞k0，上式可以化简为

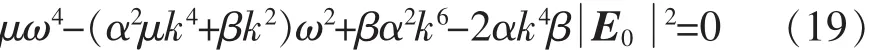
方程(20)的解为

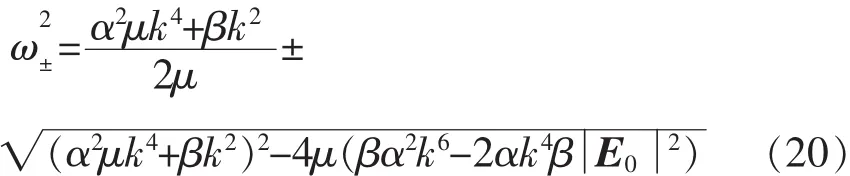
当且仅当

时，方程(20)有虚根，在这种条件下，调制不稳定发生.从方程(21)，我们得到增长率Γ=Im（w）满足

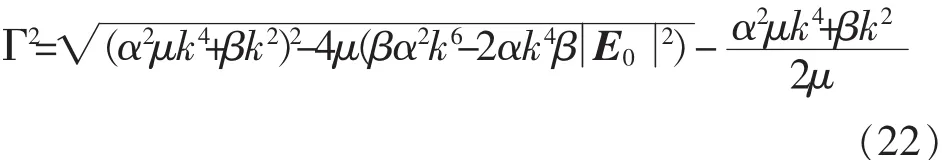
这种情况下，增长率满足

2 数值计算与结果讨论

对于两种特殊情况：θ±=π/2与θ±=0，我们解析地给出了相应调制不稳定性的增长率方程(22)和(24).为了得到色散关系的一般图像，我们有必要数值求解复杂的色散方程(18)，研究不同角度下的调制不稳定性.很显然，对于同一组参数，方程(18)有六个复数根，

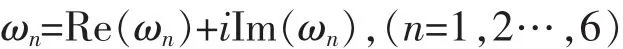
但其中必有一个最大虚根，它就是诱发场的最大增长率.在飞行器远尾区图1与图2分别给出对于不同增长率Γ随波数k的Δ变化.文章中，我们选取初始场满足湍动波条件·E（ξ，τ=0）=0，温度Ti=Te=3000 K，其对应的α=9×105.可以看出，最大增长率对角度θ的变化非常敏感，并且当θ=0，也就是k‖E0时，诱发场的增长率最大，E∝eΓt，其中，Γ由方程(25)给出.这里一旦给定初始值，便很容易求得诱发场的强度[9].图2给出了当θ=0时，不对应的增长率.从图中可以看出，随增大，诱发场的特征尺度变小，其强度变大.很显然，场坍塌至空间小尺度范围，并伴随着密度空穴的产生.

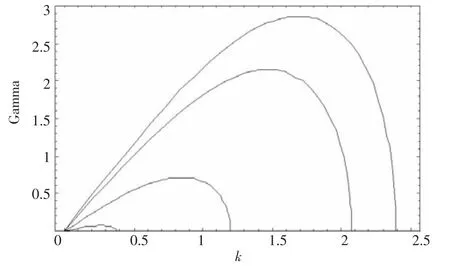
图1 E02=2.87时，不同角度θ所对应的调制不稳定性增长率，图中曲线自上而下依次对应θ=0，π/6，π/3，π/2

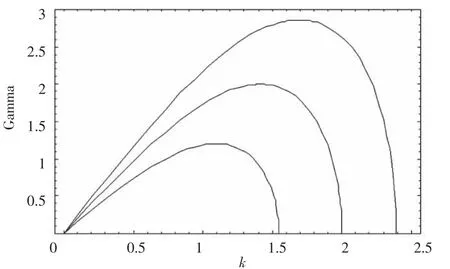
图2 θ=0时，不同泵波场强度E02所对应调制不稳定性增长率，图中曲线自上而下依次对应E02=2.87,2,1.2

3 结论

理论分析和数值结果表明，当k‖E0时调制不稳定性是最大的，我们定义图1与图2中每条曲线的最高点为Γmax，其对应的波数为kmax，从图2不难看出，场的特征尺度lc～1/kmax∝1/E0，最大增长率Γmax∝E0.由此可知，诱发场的特征尺度随着场强度的增加而减小，这表明场在经历坍塌过程，从方程（5）可以看出，这个过程伴随着密度空穴的形成，这与胡等人[9]的结果一致；此外，湍动场越强，诱发场增长越快，这表明湍动场有助于诱发场局域结构的形成以及密度空穴的产生，这非常类似于激光与等离子体相互作用产生非线性实体的情况[12].

文章从飞行器远尾区诱发场的非线性控制方程（1）、（5）出发，通过线性分析得到扰动的色散关系(方程(18)).结果表明，在飞行器远尾区形成的诱发场是调制不稳定的，对于均匀泵波场，调制不稳定性将导致场的坍塌，使得等离子体密度发生变化，形成密度空穴，这为隐形飞行器的探测提供可能的理论指导，对国防科技起重要作用.

[1]廖晶晶，刘三秋.空间飞行器远尾区电双层形成的数值模拟[J].南昌大学学报，2010，34(1)：56-61.

[2]李晓卿.等离激元坍塌动力学[M].北京：中国科学技术出版社，2004：390-412.

[3]Liu S Q，Liao J J.An investigation of electric double layer caused by space vehicles moving through ionosphere[J].Phys.Scr.，2010，82(4)：45902-45908.

[4]廖晶晶，刘三秋.空间飞行器诱发的密度空穴、高频场包络及电双层腔子[J].江西科学，2010，28(1)：16-18.

[5]Lieberman M A，Charles C.A theory for formation of a low pressure，current-free double layer[J].J.Phys.D：Appl.Phys.，2006，39(15)：3294-3304.

[6]Chabert P，Lichtenberg A J，Lieberman M A.Theory of a doublelayer in an expanding electronegative plasma[J].Physics of plasmas，2007，14(9)：93502-93512.

[7]罗青，汪静，胡涛平.空间飞行器近尾区内场和密度空腔的研究[J].核聚变与等离子体物理，2011，31(3)：278-282.

[8]杨勇，赵正予，Anisimov I O.从空间飞行器入射进电离层的调制电子束产生的高频波辐射[J].空间科学学报，2006，26(2)：86-91.

[9]胡涛平，李晓卿.空间飞行器远尾区内等离子体与场的相互作用[J].天文学报，2003，44(1)：87-95.

[10]邱鑫，李艳玲，钟阳万.基于频率失谐的混沌同步状态转换的研究[J].江西理工大学学报，2011，32(3)：77-80.

[11]刘勇，刘三秋.横等离激元与对等离子体的非线性相互作用[J].核聚变与等离子体物理，2011，31(1)：19-23.

[12]Liu Y，Liu S Q.Density cavitons with spontaneous magnetic fields in relativistic plasmas[J].Physical scripta，2010，81(6)：65501-65506.

Modulational instability for an induced field in the far-wake region of a space vehicle

LIAO Jing-jinga,WANG Su-mina,LI Yan-lingb

(a.Faculty of Applied Science;b.Faculty of Information Engineering,Jiangxi University of Science and Technology,Ganzhou 341000,China)

Non-steady interaction between spacecraft with antenna and plasma can be described by a set of nonlinear coupling equations of high-frequency field and density disturbance in the far wake region of space vehicles.On the basis of the nonlinear coupling equations,the dispersion equation of perturbation is obtained through linear analysis.Theoretical analysis and numerical calculation indicate the induced field is modulational unstable and will collapse into spatial localized structures,meanwhile,density cavitons will be generated.The characteristic scale and maximum growth rate of the induced field depend not only on the angle between the amplitude of pump waves and perturbation wave vector,but also on the energy density of pump waves.

space vehicle；modulational instability；density caviton；collapse

O534

A

2012-04-12

江西省高校省级教改课题（JXJG118110）；江西省教育厅2012年度青年基金项目（GJJ12355）；江西理工大学科研基金项目(jxxj11170)

廖晶晶（1986-），女，助教，主要从事激光等离子体等方面的研究，E-mail：ivy986428@163.com.

2095-3046（2012）03-0086-04