利用原子系数矩阵法确定复杂反应体系独立反应的方法探讨与改进
陈 博,朱建华,岳长涛
(中国石油大学化工学院,北京 102249)
利用原子系数矩阵法确定复杂反应体系独立反应的方法探讨与改进
陈 博,朱建华,岳长涛
(中国石油大学化工学院,北京 102249)
为了简化对复杂反应体系的表征,原子系数矩阵法被用于确定化学反应方程式未知的复杂反应体系的独立反应数及独立反应,但由于原有原子系数矩阵法在选择非关键组分原则方面的缺陷,导致其在应用过程中可能出现无解现象。基于对原子系数矩阵的分析,提出对原子系数矩阵进行初等行变换,然后选取变换后原子系数矩阵最大线性无关向量组;当原子系数矩阵的秩为R时,通过对调列向量的方法,将最大线性无关向量组置于原子系数矩阵的前R列,而该最大线性无关向量组对应的组分可被选作该复杂反应体系的非关键组分。对非关键组分选取原则的上述改进,可使利用原子系数矩阵法确定复杂反应体系独立反应的方法更为严谨,避免原有方法在应用过程中出现的无解现象。实例分析结果表明,对利用原子系数矩阵法确定复杂反应体系独立反应的方法改进是行之有效的。
原子系数矩阵 独立反应 化学计量系数 最大线性无关向量组 非关键组分
化学计量方程给出了参与化学反应的物种消耗量或生成量的比例关系。复杂化学反应体系通常由多于两个的化学反应构成,如果其中某一化学反应的化学计量方程不能由体系中其余化学反应的化学计量方程线性组合表示出来,则称其为独立反应[1],独立反应的最大数目被称为复杂反应体系的独立反应数。
在一个复杂反应体系中,可以确定一组独立反应,并通过这些独立反应的线性组合得到复杂反应体系中其它的非独立反应,因此可以借助这组独立反应表征整个复杂反应体系,这样在对复杂反应体系表征时可起到事半功倍的效果。通过确定复杂反应体系的独立反应,可以计算复杂反应体系中各组分的变化量,减少对复杂反应体系物料衡算及能量衡算的工作量,对确定反应器的进料配比、产物组成,以及反应器的设计及操作条件选取具有重要的指导意义。
在现有的教科书及发表的文献中,利用原子系数矩阵法确定复杂反应体系独立反应的方法并不完善,在实际应用中会因为非关键组分的选取不当而导致方程组出现的无解情况,这表明现有的选取复杂反应体系非关键组分的方法尚不够严谨。鉴于此,本文通过数学推导,对利用原子系数矩阵法确定复杂反应体系独立反应的方法进行深入的探讨并加以改进,从而使利用原子系数矩阵法确定复杂反应体系独立反应的方法更为严谨、有效。
1 方法原理
1.1 过程及推导
在简单反应体系中,独立反应一目了然。然而对于复杂反应体系,由于组分数及化学反应方程数目的增多,需要借助一定的方法方可确定复杂反应体系的独立反应数及一组独立反应。
对于一个指定的化学反应,化学计量方程给出了参与反应的组分消耗量或生成量的比例关系;化学方程式遵循质量守恒定律,等号两边各原子的种类及数目相等,也即反应前后参与反应的原子种类及数目是不变的,应用于化学反应的质量守恒实质上是原子守恒,也即反应物转化的质量必然等于生成产物的质量。
对于有n个组分参与的单一反应,有:
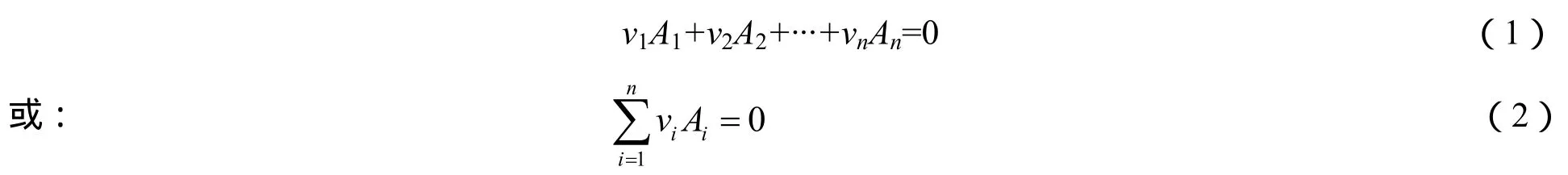
式中:νi为i组分的化学计量系数,表示该反应中i组分相对于其它组分反应的摩尔数;Ai表示i组分。
对于由n个组分、m个反应构成的复杂反应体系,可表示为:

其化学计量方程可用紧凑形式表示为:

式中:i为组分序号;j为反应序号;νji为第j个反应中第i个组分的化学计量系数。
将式(4)改写为矩阵形式,有:

在反应过程中,各组分中的原子可重新组合形成其它组分,但每种原子的数目在反应前后是恒定的,基于这一原理,引入原子系数矩阵。若已知化学反应体系的所有组分,假设组成复杂反应体系所有组分的原子共有s种,则组分Ai的化学式可表示为体系中所有原子E1~Es的线性组合,即:

式中:Zji为构成Ai组分的第j种原子的系数,其值应为正整数或零。
这样,可将各组分表示为各种原子的加和形式,故复杂反应体系的组分向量A的表达式可表示为:

通常把原子向量(E1,E2,··,ES)T前的矩阵转置,得到:

式(9)即为该复杂反应体系的原子系数矩阵。
因此,当已知一个复杂反应体系中所有组分的分子式时,便可确定该复杂反应体系的原子系数矩阵Z。
分析式(8)可知,在化学反应中不会发生不同种类原子间的转化,因此要使(8)式成立,需使νZ T=0,而转置后的ZνT=0也应成立。
对于方程组:
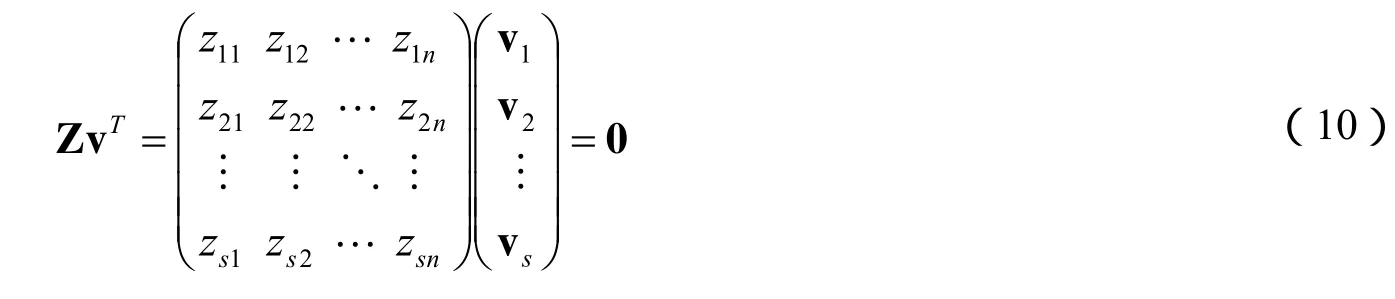
如果原子系数矩阵Z的秩为R,则方程组中应有R个线性独立的方程,因此方程组(10)中有(n-R)个独立变量[2],由于每个独立变量对应于一个独立反应,故复杂反应体系的独立反应数也应为(n-R),因此需选择(n-R)个组分作为关键组分。当确定(n-R)个组分的化学计量系数后,其余R个非关键组分的化学计量系数可通过计算确定。
1.2 实际应用中的问题及误区
由于原子系数矩阵法是通过计算非关键组分的系数矩阵进而确定独立反应的,因此非关键组分的选取显得尤为重要。对于给定的复杂反应体系,独立反应数和关键组分数是确定的,但选择哪些反应作为独立反应,哪些组分作为关键组分则并不是惟一的。朱开宏等[1]建议在选择关键组分时需使非关键组分所包含的元素数不少于原子系数矩阵的秩,否则会使方程组存在无穷多组解,但此限定并不严谨。根据线性代数理论,选择非关键组分是为了通过对其进行线性组合,从而使其中的原子以线性加和方式构成所有的关键组分。因此非关键组分不仅要包含构成复杂反应体系组分的所有原子种类,而且各非关键组分所包含的不同种类的原子之间也不能存在线性限定关系,如下文中将要提到的比例关系和/或加和关系,否则方程组(10)将出现无解现象。
此外,对于一些相对简单的复杂反应体系,文献[3]认为当其组分数n大于构成这些组分的原子种类数s时,独立反应数应等于二者之差,即独立反应数等于(n-s)。据上述讨论可知,独立反应数应等于关键组分数,并且均等于(n-R),由于原子系数矩阵的秩R与行数s并不总是相等的,如由C2H4、C4H8、C6H12构成的复杂反应体系的n=3,R=1,s=2,因此利用该方法得到的结果并不可靠。
2 实例分析
实例1,为了保证我国能源战略的安全性,以我国相对较为丰富的煤炭资源为原料,通过用煤合成的甲醇生产低碳烯烃,是发展非石油资源生产乙烯等重要化工产品的核心技术,目前我国正自主开发由甲醇制备低碳烯烃的MTO、MTP工艺。现以甲醇制丙烯反应体系为例,来阐述利用原有原子系数矩阵法确定复杂反应体系独立反应方法的不足。文献[4]中假设该复杂反应体系由下列组分:CH3OH、C2H4、C3H6、H2O、CH4、C2H6、C3H8、C4H10、C4H8、CO2、CO及H2组成,现利用原有的原子系数矩阵法确定一组独立反应。
该复杂反应体系的原子系数矩阵为:

对其进行初等行变换,有:
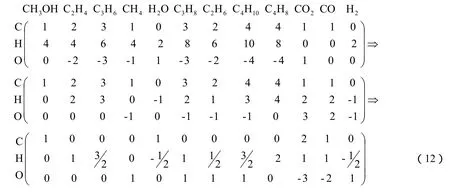
由矩阵(12)可知,该复杂反应体系原子系数矩阵的秩R为3,而反应体系的组分数为12,故该反应体系的独立反应数为12-3=9。
根据原有的原则[1],选取含有组成该复杂反应体系组分全部原子种类的R个组分为非关键组分,如选择CH3OH、C2H4和C3H6三个组分为非关键组分,则其余的H2O、CH4、C2H6、C3H8、C4H10、C4H8、CO2、CO和H2为关键组分。假设该复杂反应体系独立反应的化学计量系数矩阵为:

依据原子守恒原理有:
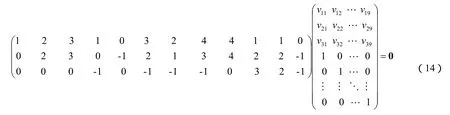
由方程组(14)可知,在进行氧原子衡算时,将会出现无解方程,进而造成方程组(14)无解。出现这种情况的原因在于选择非关键组分时,虽然符合了非关键组分应含有组成该复杂反应体系组分所有原子种类的要求[1],但组分C2H4、C3H6中C、H两种原子的系数比均为1:2,呈现相同的比例关系,因此不能通过非关键组分的线性组合表示复杂反应体系中所有的关键组分,进而导致方程组(14)出现无解现象。
现考虑实例2,对于实例1中所述的甲醇制丙烯复杂反应体系,如果选择的复杂反应体系非关键组分中含有的原子系数存在一定的加和关系,也将导致方程组(10)出现无解现象,现推导如下:
甲醇制丙烯反应体系的原子系数矩阵亦可表示为:

对其进行初等行变换,有:

依据文献[1]关于非关键组分的选取原则,选取CH3OH、C2H4和H2O作为该复杂反应体系的非关键组分,其中1个C2H4分子与2个H2O分子中包含的C、H和O原子的个数加和值分别等于2、8、2,均为1个CH3OH分子中包含的C、H和O原子数目的2倍,由上述对原子系数矩阵进行初等行变换的结果可知,这种情况仍无法进行O原子的衡算,进而导致方程组(10)无解。
综上所述,在选取复杂化学反应体系的非关键组分时,除应符合文献[1]关于非关键组分的选取原则外,各非关键组分包含的不同种类原子的系数间不能存在固定的比例关系,如实例1中展示的比例关系;此外所有非关键组分中各种原子的数目之间也不能存在加和关系,否则均会减少非关键组分对应的列向量组的秩,最终导致求解独立反应化学计量系数的方程组(10)出现无解现象。综上所述,利用原子系数矩阵法确定复杂反应体系独立反应时选择非关键组分的原有方法[1]并不严谨,因此,需提出更为科学、严谨及有效的选择非关键组分的方法。
3 解决方案
在利用原子系数矩阵法确定由多原子、多组分组成的复杂反应体系的独立反应时,由于无法利用直觉确定非关键组分间存在的比例和/或加和关系,因此需借助线性代数方法确定复杂反应体系的非关键组分。
线性代数中关于最大线性无关组的概念,即:对于一个给定的向量组α1,α2,…αs,若存在一组向量α1’,α2’,…αp’(1≤p≤s)线性无关,且向量组α1,α2,…αs中的任一向量皆可由向量组α1’,α2’,…αp’线性表示,则称向量组α1’,α2’,…αp’为α1,α2,…αs的一个最大线性无关向量组。对于一个复杂反应体系,选取非关键组分的关键,是寻求一个最大线性无关的列向量组A0,而该列向量组可线性表示该复杂反应体系原子系数矩阵Z中的任一列向量,而列向量组A0对应的组分可被选为复杂反应体系的非关键组分。
现引用文献[6]给出的简捷方法确定指定原子系数矩阵的一个最大线性无关列向量组:首先对指定的原子系数矩阵进行初等行变换,得到具有R(原子系数矩阵的秩)个非零行的行阶梯型矩阵,而各行中首个非零元素所在列对应的向量构成的向量组,即为原子系数矩阵列的一个最大线性无关向量组,同时,各行中首个非零元素所在列对应的组分即为被选的复杂反应体系的非关键组分。
如实例1中,将复杂反应体系的原子系数矩阵经初等行变换后可得到如式(12)所示的行阶梯形矩阵,该阶梯矩阵有三个非零行,即原子系数矩阵的秩为3,因此各非零行的首个非零元素所在的第1、2和4列对应的列向量即可构成该原子系数矩阵最大线性无关的列向量组,选择最大线性无关列向量组对应的CH3OH、C2H4和 CH4三个组分作为该复杂反应体系的非关键组分,然后,将经过初等行变换后的原子系数矩阵中的第3列与第4列对调,可得到如下所示的新原子系数矩阵:

假定9个独立反应的化学计量系数矩阵为:
据式(10)有:
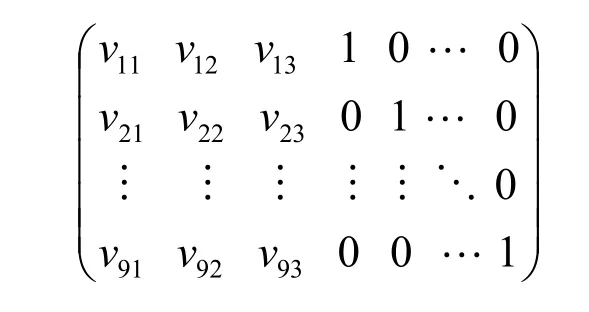
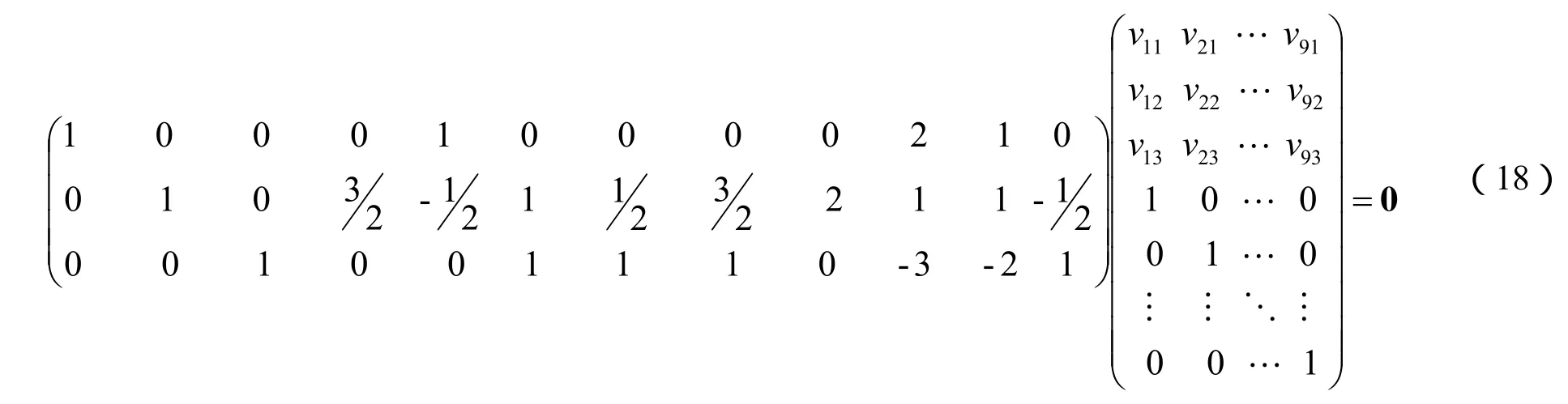
求解矩阵方程(18)可得:
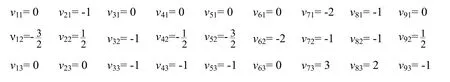
由于该复杂反应体系的9个独立反应中各组分的化学计量系数已被确定,可由式(5)确定9个独立反应,结果如下所示:

同理,可将选取原子系数矩阵最大无关向量组的方法,应用到实例2所述的情况,选择式(16)中的第1、2及4列作为最大线性无关的列向量组,而其对应的CH3OH、C2H4及C3H8作为该复杂反应体系的非关键组分,并将经过初等行变换后原子系数矩阵中的第3列与第4列对调,可得到新的原子系数矩阵,结果如下所示:
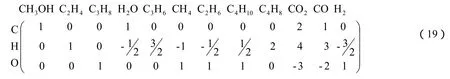
求解相应的矩阵方程,也可确定9个独立反应,分别为:

综上所述,利用选取复杂反应体系原子系数矩阵中最大线性无关列向量组对应的组分作为复杂反应体系的非关键组分的方法,可避免原有方法中由于非关键组分的选择不当而导致的方程组(10)无解现象的出现,使利用原子系数矩阵法确定复杂反应体系的独立反应成为一种更为严谨、有效的方法。
由上述的实例分析可知,对于一个化学反应方程式未知的复杂反应体系,可根据该复杂反应体系包含的所有组分以及构成这些组分的原子种类数,首先列出该复杂反应体系的原子系数矩阵,其次对该原子系数矩阵进行初等行变换,确定其最大线性无关的列向量组,并将该最大线性无关的列向量组通过对调列向量的方法置于原子系数矩阵的前R列(R为原子系数矩阵的秩),并再次利用初等行变换的方法将该最大线性无关的列向量组化为秩为R的单位矩阵,而该单位矩阵列向量对应的组分可被选作该复杂反应体系的非关键组分,这样即可避免在确定独立反应的化学计量系数时出现的方程无解现象,使利用原子系数矩阵法确定复杂反应体系独立反应的方法更为严谨有效。
4 结 论
a)在利用原有的原子系数矩阵法确定由多原子、多组分组成的复杂体系独立反应时,仅选择组分中所包含元素数不少于原子系数矩阵秩的组分作为非关键组分的原则并不严谨,有可能导致在求解独立反应化学计量系数矩阵方程时出现无解现象。
b)当复杂反应体系中的组分数大于组成该复杂反应体系的原子种类数时,独立反应数并不一定等于二者之差。
c)为解决原有方法存在的问题,本文对利用原子系数矩阵法确定复杂反应体系独立反应的方法提出以下改进,即:首先列出该复杂反应体系的原子系数矩阵,其次对该原子系数矩阵进行初等行变换,确定其最大线性无关的列向量组,并利用对调列向量的方法将该最大线性无关列向量组置于原子系数矩阵的前R列,最后将该最大线性无关的列向量组变换为秩为R的单位矩阵,而该单位矩阵列向量对应的组分则可选作该复杂反应体系的非关键组分,这样就可避免在确定独立反应的化学计量系数时出现的方程无解现象,使利用原子系数矩阵法确定复杂反应体系独立反应的方法更为严谨有效。
[1]朱开宏, 袁渭康. 化学反应工程分析 [M]. 北京: 高等教育出版社, 2002:1-23.
[2]Степанов, 斯捷潘诺夫. 物理化学中的线性代数方法 [M]. 王正刚, 译. 北京: 科学出版社, 1982:174.
[3]兴长策, 陈国伟. 相律中独立反应方程数的线性解法 [J]. 辽宁工学院学报, 2001, 21(4):52-54.Xing Changce, Chen Guowei. The linear solving processes of independent reaction equation numbers in phase rule [J]. Journal of Liaoning Institute of Technology, 2001, 21(4):52-54.
[4]郝西维, 张军民. 甲醇乙烯烷基化反应体系热力学分析 [J]. 化学工程, 2010, 38(11):64-67.Hao Xiwei, Zhang Junmin. Thermodynamic analysis of alkylation reaction of methanol and ethylene [J]. Chemical Engineering, 2010,38(11):64-67.
[5]同济大学数学系. 工程数学线性代数 [M]. 北京: 高等教育出版社, 2007:90-91.
[6]魏占军. 关于求向量组最大无关组的矩阵方法 [J]. 石家庄铁道学院学报, 1993, 6(2):89-93.Wei Zhanjun. On the method of elementary operation of matrix for finding a maximal independent system of vectors [J]. Journal of Shijiazhuang Railway Institute, 1993, 6(2):89-93.
The Improvement on Method of Determining the Independent Reactions
for Complex Reacting System via Atomic Coefficient Matrix Method
Chen Bo,Zhu Jianhua,Yue Changtao
(College of Chemical Engineering, China University of Petroleum, Beijing 102249, China)
In order to simplify the characterization of complex reacting system, it is necessary to determine the number of independent reactions and one set of independent reactions. For the case in which reaction equations were unknown, the atomic coefficient matrix method could be used to determine the independent reactions and their number of complex reacting system. However, the original method might be no solution in application since the definition principle fornon-key component was imprecise. Based on the analysis of the atomic coefficient matrix, the improvement on the original atomic coefficient matrix method was put forward by this paper, i.e., via elementary line transformation for the atomic coefficient matrix, one set of the maximal linearnon-relevant columns were determined. When the rank of atomic coefficient matrix wasR, the set of maximal linearnon-relevant columns were located on the front R columns by exchange the column vector. Finally, the components corresponding to maximal linearnon-relevant columns were chosen asnon-key components of specified complex reacting system. The results of case study demonstrated that by such improvements on the selection ofnon-key components, the no solution phenomenon of atomic coefficient matrix method could be avoided.
atomic coefficient matrix; independent reaction; stoichiometric coefficien; maximal linearnon-relevant columns;non-key component
TQ03.3 文献标识码:A
1001—7631 ( 2012) 01—0057—08
2011-11-08;
2012-02-21
陈 博(1986-),男,硕士研究生;朱建华(1963-),男,教授,通讯联系人。E-mail:secondzhu@sina.com
——以某大厦地下停车场第二层开挖管道工程为例*

