斜齿轮副轮齿啮合刚度变量计算用的参数化的数值模型

J Hedlund A Lelical

1 前言

近代齿轮研究表明齿轮的啮合刚度和传动误差是在齿轮传动中主要的振动激励源［1］，大多数齿轮动力学模型是利用啮合刚度或传动误差描述齿轮啮合相互作用的激励。

齿轮设计中的最常见问题是确定齿轮几何参数的最佳组合。这些参数应该有可能改进激励和振动分析的各种各样效能。齿轮啮合刚度和传动误差的精确预测要求一个有效的数值方法。有限元（FE）方法主要用于计算变形，应力和负载分布［2－12］，但是FE方法也可以用来预测参数激励，即啮合刚度变量。采用典型FE方法的缺点是其模型不易变化，特别对于精确的几何生成。此外，为设计目的由于高非线性Hertzian接触计算时间很可能太长。采用FE方法的优点是可以采用于标准计算无效的那些情况。

为齿轮设计目的FE计算的有效利用，要求其几何生成必须参数化。此外，振动测量值在正常频率分析范围内，所以如果计算模型提供的结果也能在该范围其优点是明显的。

本研究介绍了为估算圆柱齿轮参数激励的一个计算模型，开发该模型只作为实际齿轮副要求的有效的分析和比较，而不需要计算昂贵的模型，该整个激励模型是参数化的。因此，在时间和频率范围内求得啮合刚度变量。

2 结构变形FE模型

为结构变形分析基于FE方法开发了一种计算模型，该模型开发的数值数据，用参数化几何模型产生一个单元啮合建立的，该几何模型仿真齿轮加工，即滚切过程。该方法基于大量数值计算要点和其同时产生的结果［13，14］，它允许与通常的渐开线几何学差异。该方法的详细阐述和其精确度问题将在另文中介绍。

该FE方法采用8节点三线六面体单元［15］，采用Matlab作为编程工具。在8节点三维单元状况中，采用Gauss点2＊2＊2，它在8节点六面体单元中给出可靠的积分［16］。该FE方法包含针对轮齿及其基础的一个参数化网络，该网络在轮齿接触过程中分别建立的，制作该网络利用基本的啮合概念［17］，它包含单元和节点编号。该基本啮合可以利用轮齿齿面几何学自动扩展超过确定的范围。用最接近有效座标点找出扩展开拓三维表面几何矩阵，所以适合任何曲线或不要求插值。

啮合过程是参数化的仅需要以下数值：单元参量为啮合宽度，长度，高度和基础深度方向，此外产生单元啮合可以用重量因数修正，为精确起见，允许啮合密度在确定范围内变化。一轮齿啮合实例示于图1。两小齿轮和大齿轮啮合可以独立修正。例如，用一指数方程建立轮齿基础密度造成啮合密度正好在轮齿下方，这是变形和应力集中的危险截面。建立的基础啮合利用椭圆形确立单元啮合边界。采用椭圆半轴作为变数，半椭圆基础可以改变。椭圆半轴用af和bf表示。

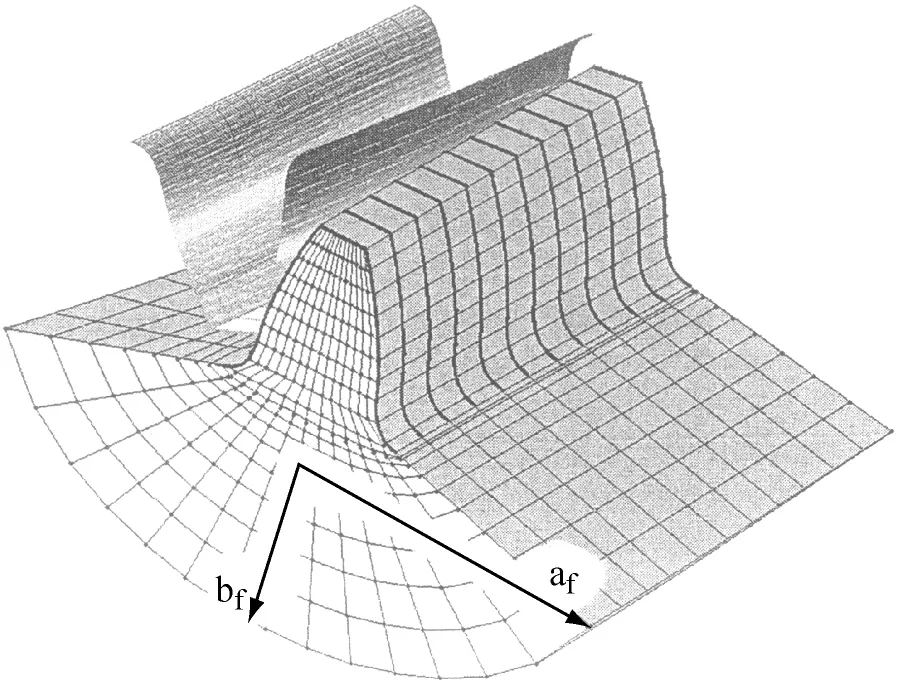
图1 轮齿啮合和其基础的实例Fig.1 Example of the meshing of the tooth and its foundation

主刚度矩阵和主力矩阵采用自由计数器技术进行组合。当量节点负载位于节点，与接触线位置相对应，它确定于一个未变形状况。但是如果必要的话，可以采用逐次逼近法在变形状况确定接触线。用稀疏矩阵来确定矩阵组合和解，因为矩阵许多项为零。在稀疏矩阵形式内用一个直接的方法求解，并从而求得节点位移和应力。

3 HERTZIAN接触

渐开线正齿轮轮齿沿啮合线接触，其特征模拟作为一恒定变化的滚子接触，滚子半径可以按渐开线齿轮几何学计算。齿轮啮合循环近似于许多不连续的滚子接触，其赫茨（Hertzian）参量可采用压力和接触区计算。

对于斜齿轮和非渐开线齿轮，其齿面曲率半径可以用沿啮合线外接圆半径法有效确定。该方法可数值计算齿轮接触几何参数。用找出给定点（图2）的外接圆半径rc来数值确定曲率半径。对于正齿轮在齿廓方向求得该点，在斜齿轮情况，应在接触线的法线方向计算该半径。选择座标点位置表明实际的赫茨接触求得精确的接触半径。

图2 外接圆和外接圆半径Fig.2 Circumcircle and Circumradius

如果采用典型的齿冠值，在斜齿轮接触方面的椭圆率是大的，而简化的赫茨公式不能包括大的椭圆率，这就意谓必须采用拓宽该公式，如果一简化的解是一重要的因数，那么应首先近似采用赫茨线接触公式。

4 啮合刚度变量

确定的啮合刚度作为所有啮合轮齿之间的刚度，本研究利用单对轮齿的刚度值构成啮合刚度。分别和结合结构刚度用连续弹簧原理计算接触刚度确定啮合刚度，在计算的结构刚度中包含轮齿弯曲，剪切和齿根根切等现象。轮齿基础啮合尺寸可以改变所述齿轮体刚度，结构刚度值沿齿面法向计算。利用啮合轮齿对之间的理想接触线确定当量节点负荷，采用节点位移位于齿面4单元层以下确定结构刚度，这种方法使局部接触变形对结构刚度计算影响最小。它假定相邻轮齿的负荷不影响所述轮齿的变形，这是合适的，因为对于正齿轮仅采用一对轮齿可确定其啮合刚度［18］，忽略摩擦力的影响。

必须考虑非线性接触对参数激励的影响，采用赫茨理论对椭圆或线接触或用FE基础接触分析可计算接触刚度值。用适度或少数单元赫茨理论比FE基础接触分析更精确，但采用FE方法的优点可考虑边缘接触。本文采用赫茨线接触公式。

采用弹簧连续原理分别计算结构和组合局部接触刚度值，该原理示于图3。沿一当量啮合线在齿面宽度中间（图4）模拟圆柱齿轮副的啮合刚度变量，这按照实际啮合发生在啮合面［19，20］上。

图3 刚度连续原理Fig.3 Principle of Stiffness in Serier

图4 斜齿圆柱齿轮当量啮合线和啮合面Fig.4 Equivalent line of action and the plane of action for helical cylindrical gears

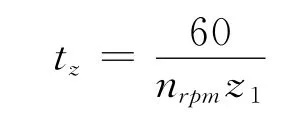
从而由啮合开始到结束的总啮合时间确定为

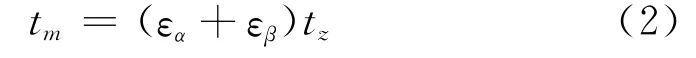
实例单轮齿对刚度和齿轮副的啮合刚度示于图5。沿当量啮合线研究刚度的变量。描述单齿对刚度矢量用分支表示其他轮齿接触，假定各轮齿具有相的刚度特性。用各单齿对刚度矢量和得出齿轮副的啮合刚度矢量。采用总啮合刚度矢量计算承载准静态传动误差，还可求解沿啮合线啮合轮齿间载荷分布。

图5 单轮齿对刚度（Kmi（t））和总刚度（ΣKmi（t））矢量Fig.5 Single Stiffness（Kmi（t））and total stiffness（ΣKmi（t））vectors

4.1 福里哀频谱

变换啮合刚度变量为其福里哀级数使它可表示为啮合刚度激励在频率范围内。它可与齿轮几何参量对激励频率造成的影响作比较。参考文献［11］介绍了该方法的原理。它还可能使计算结果和实验结果比较，这是一种典型的操作并表示在频率范围内。

采用这种方法形成的刚度激励的福里哀频谱如图6所示，在该图中，用纵轴表示振幅，该原始标志（啮合刚度变量）和其福里哀级数近似由上辅线图可见；其福里哀系数（啮合频率和它的谐波）示于下辅线图。该标志曲线的形状确定相对高的谐波。

图7上辅线图示啮合刚度变量和对应的福里哀级数，下辅线图示测量齿轮试验台自然频率特性（实线）和计算啮合刚度变量（线条）的福里哀频谱的一个实例，当激励频率等于自然频率时发生共振。由于这个原因，涉及到有关低振动值必需避免激励与自然频率之间重合。

在齿轮动力学和齿轮几何数据的设计中，如螺旋齿轮，可以修正改变啮合刚度变量的形式，即其尺寸和福里哀系数的定位。而且，自然频率可以用修正轴和轴承的刚度或齿轮的惯性质量来调整。在这方面，振动性能可以控制而没有时间消耗响应计算，如图7所示，在该实例中，已选定齿轮的几何尺寸，而不存在激励和自然频率峰值间的重迭。

图6 啮合刚度变量和相应具有7个福里哀系数的福里哀频谱的实例Fig.6 Example of mesh stiffness variation and corresponding Fourier Spectrum with Seven Fourier Coefficients

图7 自然频率特性相对于激励频率分量关系Fig.7 Natural frequency behavior against excitation frequency components

5 作为设计工具的模型趋向

为设计斜齿轮要计算激励而开发的模型应集中于模型的参量化和合适的计算时间。模型的参量化使模型具有灵活性，为了在某一确实应用中最小的参数激励，在齿轮设计方面困难是找到齿轮参数的最佳组合。单轮齿对模型限制了几何偏差分析，特别在由于建立模型在小的齿形偏差的情况，即相邻轮齿对齿轮体刚度具有一个小的影响。该模型的精度不适于描述微米齿型偏差对啮合刚度变量的影响。但该模型可估算顶切的修正量，因为它对沿啮合线的平均变形比对精确的啮合刚度变化形式更加有关。该模型有可能用来计算弯曲应力。开发这个模型仅作为要求精确的效率分析，比真实的齿轮副不用计算费用昂贵的模型。

整个FE啮合可用4参量确定，啮合尺寸对刚度变量有很大的影响，但随着单元数量的增大结果改进很快。图8示参量激励矢量与每齿不同单元数间关系曲线。计算的试验齿轮副的数据列于表1。采用一个确切少的单元数可以获得参量激励的满意值，即在576和3971单元间啮合刚度变化不大，这些曲线的特性是一个更低的单元数形成的典型的波形曲线具有大的振幅。

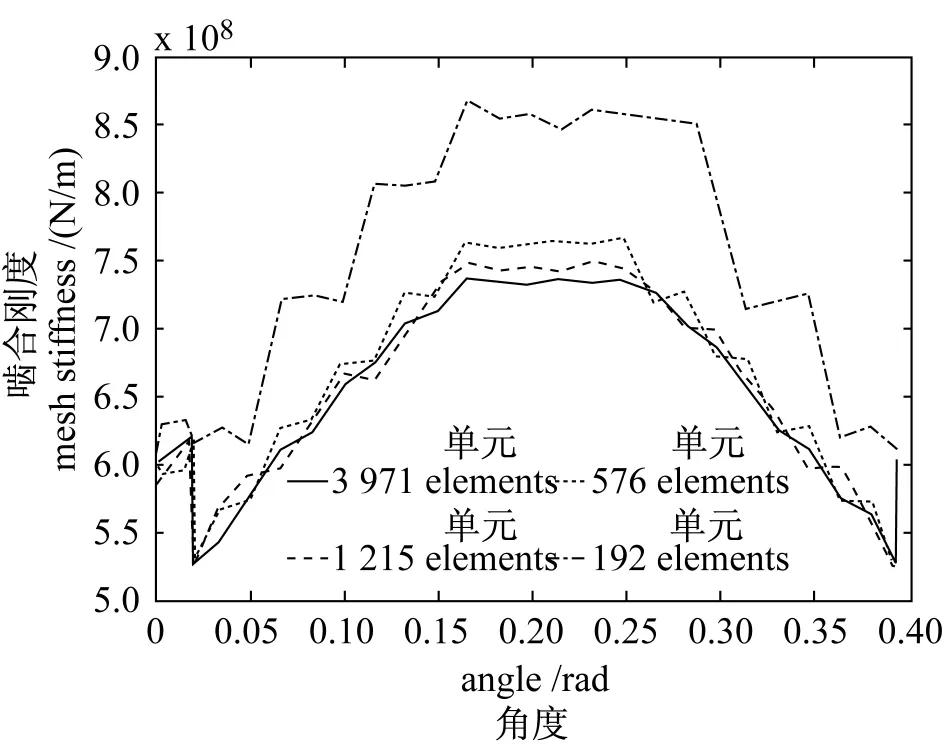
图8 采用不同每齿单元数的参量激励Fig.8 Parametric excitation using a different number of elements per tooth

表1 齿轮数据Table1 Gear data

相应于参数激励的福里哀（Fourier）系数如图9所示，该图示采用少数单元可求得福里哀图谱的合理估算。

仅采用两个参数可改变轮齿基础啮合尺寸，而轮齿啮合密度可采用加权函数确定。两小齿轮和大齿轮可以具有不同的单元数和不同的轮齿基础尺寸。模型的柔性可提供一个有效的方法研究局部接触刚度和轮齿基础柔性对参量激励和负荷分配的影响［13］。

图9 采用不同单元数的参数激励的福里哀系数Fig.9 Fourier Coefficients of the parametric excitation using a different number of elements

计算时间很大程度与FE啮合尺寸有关，齿轮几何参数的生成还要化费时间去处理，精确描述轮齿齿面几何学十分多的数据。其他增加计算时间的许多因素是在啮合线上的许多计算点，结构刚度计算在各啮合点中只需进行一次，反之，由于非线性赫茨变形总刚度变量常包含多次重复。这种重复处理增加了解题的时间。然而对于合理的精度结果，实际上重复二次三次已经足够了。由于弹性变形啮合接触在啮合线之外时，该模型还有可能对结构刚度作重复计算，但本方法很费时间，该模型计算时间不是最佳。

采用具有1800MHz处理器和1GB存储器个人计算机进行计算，各单接触点具有1000……1500个单元的计算时间约5分钟，其中包含轮齿几何自动生成的时间。在啮合线上的一典型的计算点数为50，计算整个啮合线上的结构刚度值约4小时。对于赫茨接触刚度在啮合线上取50点进行两次重复计算，第一次为设计目的可能看起来计算时间太长，但可进行粗约单元啮合进行初始计算，而利用啮合线上少量计算点以便影响激励曲线的形状，以便在选定点进行最后计算。结果两齿轮对的粗约计算可在1小时内完成。

直接采用FE解法的缺点是它对最大单元数强加一个限制，甚至要采用稀疏矩阵技术。然而这是有点理论观点，因为实际上用现有模型采用适当的单元数可以求得很好的结果。

6 结论

本文介绍了圆柱齿轮参数激励分析的一种计算模型，该计算模型利用线性三维FE方法仅针对包括轮齿基础柔性轮齿结构的变形计算。本模型为避免大的FE网格综合了接触分析和结构分析，找出赫茨公式去快速和有效地处理轮齿非线性接触。整个激励模型参数化，包括建立轮齿的FE网格。采用4参数确定整个FE网格，仅采用2参数可改变轮齿的基础尺寸，采用加权函数可确定轮齿网格密度。因而，在时间和频率范围内可求出啮合刚度变量（即参数激励）。在频率范围内正常分析振动测量值，所以当在该范围内计算模型提供结果时是它的明显优点。

本文为设计目的还研究和讨论了模型的趋向，计算表明很少的单元数能满足对啮合刚度变量的估算，在齿轮动力学的设计中，可修正齿轮几何数据来有效地改变激励的形式。这样可以在激励和自然频率间进行比较，也可作应力和负荷分布的分析，使设计趋向和计算时间达到合理的组合。（介眉译自proc.Imeche Vol.222partc：J.Mechanical Engineering Science）

References

［1］ Blankenship，G.W.and Singh，R.A comparative study of selected gear mesh interface dynamic models.In Proceedings of the International Power Transmission and Gearing Conference，13－16September 1992，ASME vol.1，pp.137－146.

［2］ Wilcox L.and Coleman，W.Application of finite elements to the analysis of gear tooth stresses.J.Eng.Ind.，1973，95，1139－1148.

［3］ Wallace，D.B.and Seireg，A.Computer simulation of dynamic stress，deformation，and fracture of gear teeth.J.Eng.Ind.，1973，95，1108－1115.

［4］ Wang，K.L.and Cheng，H.S.A numerical solution to the dynamic load，film thickness，and surface temperatures in spur gears，part I analysis.J.Mech.Des.，1981，103，177－187.

［5］ Wang，K.L.and Cheng，H.S.A numerical solution to the dynamic load，film thickness，and surface temperatures in spur gears，part II results.J.Mech.Des.，1981，103，188－194.

［6］ Coy，J.J.and Chao，C.H.－C.A method of selecting grid size to account for Hertz deformation in finite element analysis of spur gears.J.Mech.Des.，1982，104，759－766.

［7］ von Eiff，H.，Hirschmann，K.H.，and Lechner，G.Influence of gear tooth geometry on tooth stress of external and internal gears.J.Mech.Des.，1990，112，575－583.

［8］ Vedmar，L.On the design of external involute helical gears，transactions of machine elements division.Doctoral Dissertation，Lund Technical University，Lund，Sweden，1981，p.100.

［9］ Rao，C.R.M.and Muthuveerappan，G.Finite element modelling and stress analysis of helical gear teeth.Comput.Struct.，1993，49（6），1095－1106.

［10］ Steward，J.H.The compliance of solid，wide－faced spur gears.J.Mech.Des.，1990，112，590－595.

［11］ Weck，M.and Mauer，G.Optimum tooth flank corresctions for helical gears.Trans.ASME，J.Mech.Des.，1990，112，584－589.

［12］ Litvin，F.L.，Chen，J.－S.，Lu，J.，and Handschuh，R.F.Application of finite element analysis for determination of load share，real contact ratio，precision of motion，and stress analysis.J.Mech.Des.，1996，118，561－567.

［13］ Hedlund，J.and Lehtovaara，A.Modeling of helical gear contact with tooth deflection.Tribol.Int.，2007，40，613－619.

［14］ Hedlund，J.A numerical model and testing method for the evaluation of parametric excitation of cylindrical gears with shafts and bearings.Dissertation，Tampere University of Technology，Tampere，2006.

［15］ Weaver，W.Jr.and Johnston，P.R.Finite elements for structural analysis，1984（Prentice－Hall，Inc.，Englewood Cliffs，NJ 07632）.

［16］ Bathe，K.－J.Finite element procedures in engineering analysis，1982（Prentice－Hall，Inc.，Englewood Cliffs，NJ 07632）.

［17］ Nathan，M.K.，Prasanna，S.，and Muthuveerappan，G.Three－dimensional mesh generation using principles of finite element method.Adv.Eng.Softw.，2000，31，25－34.

［18］ Wang，J.and Howard，I.The torsional stiffness of involute spur gears.J.Mech.Eng.Sci.，2004，218，131－142.

［19］ Umezawa，K.，Suzuki，T.，and Sato，T.Vibration of power transmission helical gears（approximate equation of tooth stiffness）.Bull.ISME，1986，29（251），1605－1611.

［20］ Cai，Y.Simulation on the rotational vibration of helical gears in consideration of the tooth separation phenomenon（a new stiffness function of helical involute tooth pair）.Trans.ASME，J.Mech.Des.，1995，117，460－469.

附录

APPENDIX

名词

Notation

af基础齿面宽度椭圆半轴 ellipses semi－axis for foundation

b 齿面宽度 tooth facewidth

bf基础椭圆半轴 ellipses semi axis for foundation

kmi第i啮合齿对的啮合刚度 mesh stiffness of the i the meshing tooth pair

mn法面模数 normal module

nrpm小齿轮转速 rotational speed on pinion

rc圆半径 circumradius

t 时间 time

tm总－啮合时间 total meshing time

tz通过一法向基节的啮合时间 meshing time period passing a transverse base pitch

x0，y0圆心座标 circumcentre coordinates

x1，x2齿顶修正系数（表1） addendum modification coefficients（Table1 ）

xci，yci圆心座标 circumcircle coordinates

z1小齿轮齿数 pinion tooth number

z1，z2齿数（表1） tooth number（Table1 ）

α 压力角 pressure angle

β 螺旋角 helix angle

εα法向接触比 transverse contact ratio

εβ重合度 overlapratio