电场-渗流场-应力场耦合的电渗固结数值分析

王柳江，刘斯宏，汪俊波，朱 豪

（1. 河海大学 水利水电学院，南京 210098；2. 西安热工研究院有限公司，西安 710032；3. 南水北调中线干线建设管理局，北京 100038）

1 引 言

电渗是一种采用电能进行地基加固的技术[1]。Casagrande 于1939 年首次将该技术应于岩土工程中[2－3]，现已应用到斜坡、堤坝、软土地基加固等岩土工程中[4－6]。近几年，国内主要将其应用到围海造地、袋装吹填淤泥土加固、基坑降水、高速公路地基处理等工程。

目前，对于电渗法，尤其当电渗法与其他工法联合使用时，大多数还是依靠工程技术人员的经验，尚缺乏合适的设计计算理论。为克服电渗法理论上的空白，国内外众多学者对电渗固结理论展开了研究。其中，Esrig[7]最早对电渗固结理论进行了研究，然而他仅考虑了电渗的作用；Wan 等[8]通过进一步完善使其适用于电渗和堆载共同作用的情况，但只适用于一维情况。Lewis[9]在Esrig 理论的基础上 考虑了电渗过程中的电流变化。近年来，国内学者也对电渗固结理论进行了深入研究。庄艳峰，王 钊[10－11]研究了电渗过程中的电学问题，考虑了电极界面电阻的变化情况，从能量与电荷守恒角度分别推导了电渗的能级梯度理论和电荷累积理论，使其能够较好地解释电渗过程中电势的分布、电流以及土体电导率的变化规律，然而其适用性还有待于进一步验证。苏金强等[12]完善了Esrig 电渗固结理论，使之适用于二维情况，能够用于电极排形布置的情况，但对复杂电极布置的情况却不适用。李瑛等[13]通过电场等效的方法建立了等应变条件下考虑堆载-电渗联合作用的轴对称电渗固结理论，该理论虽然已经具备了较强的工程实际意义，但还是局限在饱和土的理论框架内。由于电渗是一个涉及水分、电子、离子在土体中迁移的复杂问题，在电势梯度的作用下产生负孔隙水压力，同时渗流过程中水流与土骨架变形是相互作用的，属于非饱和土范畴的渗流-变形耦合问题。因此，电渗固结理论的推导应建立在非饱和土理论的基础上，并采用有限元方法对电渗以及电渗与其他工法联合使用的情况进行计算。

本文在综合已有研究成果的基础上，基于非饱和土多孔介质力学理论，假设等温条件，忽略孔隙水体的化学作用以及各组分发生相变的影响，采用电荷守恒原理、质量守恒原理、欧姆定律以及达西定律，建立能够反映电场、渗流场以及应力场相互作用的电渗固结方程；然后，将该方程通过Galerkin法离散得到有限元计算列式，编制计算程序，对电渗的室内模型试验进行数值模拟，并与试验结果进行了比较。

2 电渗固结理论的建立

2.1 基本假定

为推导能够反映电渗过程中电场-渗流场-应力场耦合的控制方程，需做如下一些假设：

（1）假设土体内各点等温，不考虑土体内化学、相变等因素的影响；

（2）忽略土体内细颗粒发生电泳而产生的电流；

（3）土体内电荷传递满足欧姆定律；

（4）土体内水体流动满足达西定律；

（5）由电势梯度和水头梯度产生的流量可以叠加；

（6）由土体中离子移动而产生的电场相对外加电场忽略不计；

（7）固体颗粒不可压缩、水可压缩且体积压缩模量不变，孔隙气体与大气相通。

2.2 基本控制方程的建立

根据欧姆定律可得

根据电荷守恒原理，同时假设电流处于稳定状态，则得到如下方程：

式中：eR 为电流汇源项。

将式（1）代入式（2）得到电势分布的控制方程为

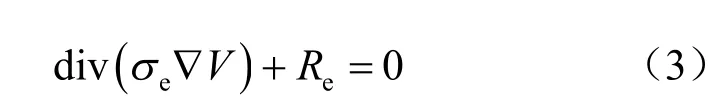
根据达西定律，水头梯度引起的流速为

式中：hK 为土体的渗透系数（m/s)；H 为水头。

由电势梯度引起的流速为

式中：eoK 为土体的电渗透系数（m2·V-1·s-1）。

根据假设（5），电渗过程中流过土体单元的流速为水头梯度和电势梯度引起的流速之和，则土体中孔隙水的渗流流速可表示为

同时根据假设（7），得到土体单元的质量守恒方程（即渗流连续性方程）为

式中：C 为非饱和土的容水度（ C =∂θw/∂uw），θw为土体的体积含水率，θw= nSr；uw为孔隙水压力；Sr为饱和度；n 为孔隙率；u 为位移矢量； Kw为水的体积压缩模量（MPa）。

将式（6）代入式（7），得到渗流场的控制方程为

土体单元的平衡微分方程为

式中：ρ、sρ 、wρ 分别为土体、土体中固体颗粒、土体中水的密度。根据假设（7），土体中的孔隙气压等于大气压，则此时土体的有效应力可表示为

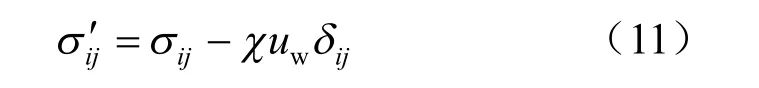
式中：σi′j为有效应力张量；δij为Kroneker 符号；χ为与饱和度 Sr有关的非线性常数，当土体处于饱和状态时， χ = 1；非饱和状态时， χ = χ（ Sr），为简化该关系式也可近似等于rS ，即 rSχ≈ 。

式（3）、（8）、（9）分别为电场、渗流场以及应力场耦合作用下的电渗固结理论的控制方程。为求解方程，将其初始条件及边界条件表示如下：

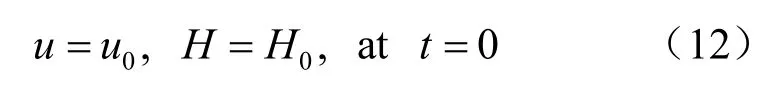
Dirichlet 边界条件：

Neumann 边界条件：

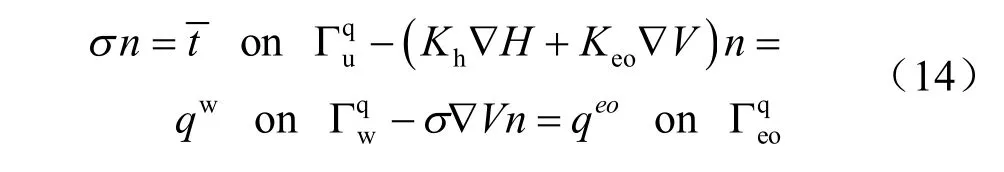
2.3 土体的非线性本构模型

本文在非饱和土多孔介质理论的基础上研究电渗作用下土体中电场、渗流场、应力场的相互作用，计算采用的参数除eoK 、hK 和eσ 之外，还包括土水特性以及力学本构模型参数。其中，土体的电导率与含水率、饱和度以及孔隙率的关系密切。根据文献[14]的试验结果，土体的电导率采用推广的阿尔奇公式换算得到：

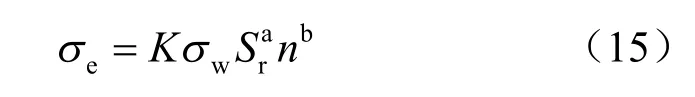
式中：K、a、b 为与土性有关的参数；wσ 为孔隙水的电导率。

非饱和土的饱和度随吸力的变化而变化，两者之间的关系式可以通过拟合土体的特征曲线而得到，本文采用van-Genuchten 模型[15]：

式中：s 为吸力（ ua- uw），根据假设（7），土体中的孔隙气压等于大气压，则吸力等于负孔隙水压力，其中规定吸力最大不超过104kPa；p0为进气值；n、m 为曲线拟合参数，m = 1 - 1/n，Se为有效饱和度：

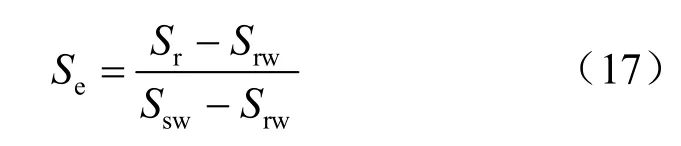
式中：rwS 为残余水饱和度；swS 为土体的最大饱和度。

土体的渗透系数采用van-Genuchten-Mualem模型[16]计算，主要考虑了非饱和土体的渗透系数与饱和度的关系：

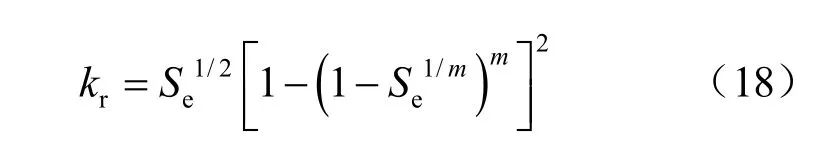
式中：rk 为相对渗透系数，将其与土体饱和状态时的渗透系数 swK 相乘即为土体的渗透系数，其余参数意义与式（16）、（17）中的相同。

电渗通常用于超软黏土的排水加固，则土体的变形预测采用能够较好地反映黏土弹塑性变形特性的修正剑桥模型，其屈服函数见式（19），该模型具有严格的理论依据，适用于正常固结和欠固结黏土的应力变形计算。

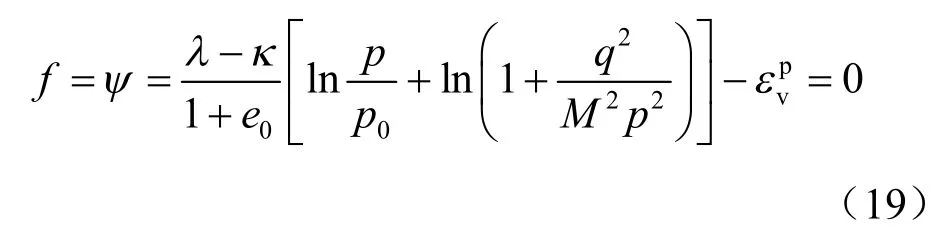
式中：p 为平均主应力；q 为广义剪应力；λ、κ 分别为土体的压缩和回弹系数；e0为初始孔隙比；M为临界状态线的斜率；为塑性体积应变，也是该模型的硬化参数。

3 控制方程的离散

Galerkin 加权余量法可以方便地运用于固体力学、流体力学和物理学问题，并且已经发展出了相对标准的推导过程，现使用加权余量法对控制方程在空间域上进行离散，离散后得到的有限元计算矩阵列式为

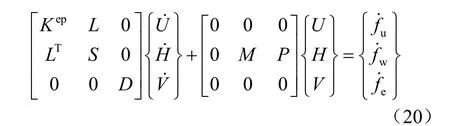
其中

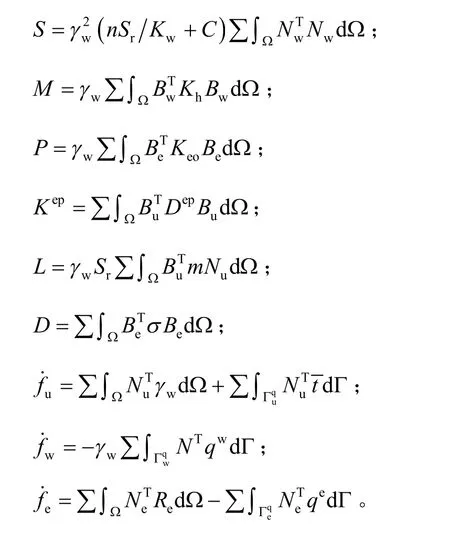
将矩阵表达式（20）以简化形式表示为

X 为主要变量，变量上方的点代表时间导数。采用向后欧拉法求解该方程组：

式中：1nX+、1nX+˙ 、1nF+为 1nt t+= 时刻对应的值，采用Newton-Raphson 迭代法对其进行求解。首先，令每一时步计算时变量的初值为

则：

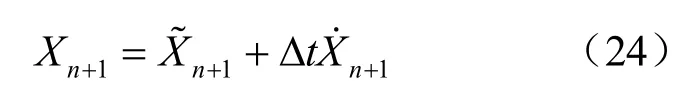
由式（22）可知，当右端项和左端项之差满足设定的收敛精度时迭代结束：

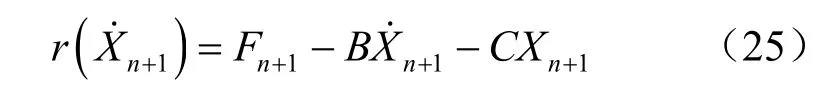
由于该问题的高度非线性，将式（24）代入式（22）后，得到如下形式：

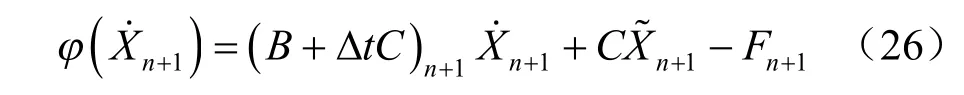
上标i 为迭代步数，下一迭代步采用的变量更新为

将更新后的变量代入式（25），若误差满足收敛要求，则结束该时步的迭代；若不满足，则代入式（27）继续进行迭代计算。由于式（20）左端的系数矩阵不对称，则采用非对称方程组求解器求解该方程组。

4 算例验证及分析

根据以上介绍的有限元计算列式和方程计算方法，自主开发了有限元计算程序。为验证该程序的正确性和适用性，本文进行了电渗联合真空排水的室内模型试验，并对其进行了数值模拟。

4.1 电渗联合真空排水模型试验

模型试验箱尺寸和布置情况如图1 所示。试验在一个80 cm×80 cm×60 cm 的模型箱中进行，采用的土样取自大连大窑湾的海相淤泥质软土，其含水率高达92.3%，土样填筑高度为50 cm；在模型箱的4 个对角处布置阳极，阴极和塑料排水板布置在模型箱中间位置；阴、阳极电极材料为直径1 cm 的钢筋，塑料排水板的截面尺寸为100 mm×4 mm；为防止土体中水分蒸发或入渗，在土体表面铺设一层土工膜进行隔水；试验中设置了位移计和振弦式孔压计（量测范围：-100～100 kPa）分别监测图1中s1，s2，s3 处的沉降和k1 处的孔压。试验开始后，在初始72 h 内先进行真空排水，尔后接通直流电源进行电渗降水，电渗电压为10 V，采用稳压方式通电，试验总共持续30 d，试验过程中每隔4 h监测一下相关数据。由于试验中排水板附近土体干裂经常发生漏气现象，真空度在试验中是变化的，由真空表测得其变化曲线如图2 所示；由于该土为海相淤泥土，具有含盐量高、电导率大的特点，且通过Miller soil box 进行试验得到土体电导率在电渗过程中确实会减小，然而在含水率大于82%时，土体电导率的减小并不十分明显；其次，电极材料采用的是钢筋，在通电条件下，阳极在该土中极易腐蚀，使其表面形成了一层保护膜，导致阳极的导电率迅速降低，增加了阳极和土样之间的接触电阻，进而使有效作用在两极间土体上的电压在试验过程中不断减小的，因此，可以认为接触电阻是电渗计算中必须考虑的因素。本文采用万用表测定有效电压，将其一探针与阴极连接，另一探针与50 cm 长的铜线连接后作为加长的探针，插入阳极边上的土体中。试验中，探针与阳极之间的距离设为4 mm，该值相对试验土样尺寸来说较小，因此，探针与阳极之间的电势差可近似认为由接触电阻引起。图3为试验过程中作用在两极间土体上有效电压的实测值。整个试验相关的结果示于图5～9 中。

4.2 计算模型及条件

图1 电渗联合真空排水模型试验示意图 Fig.1 Schematic diagrams of model test of electroosmosis combined with vacuum drainage

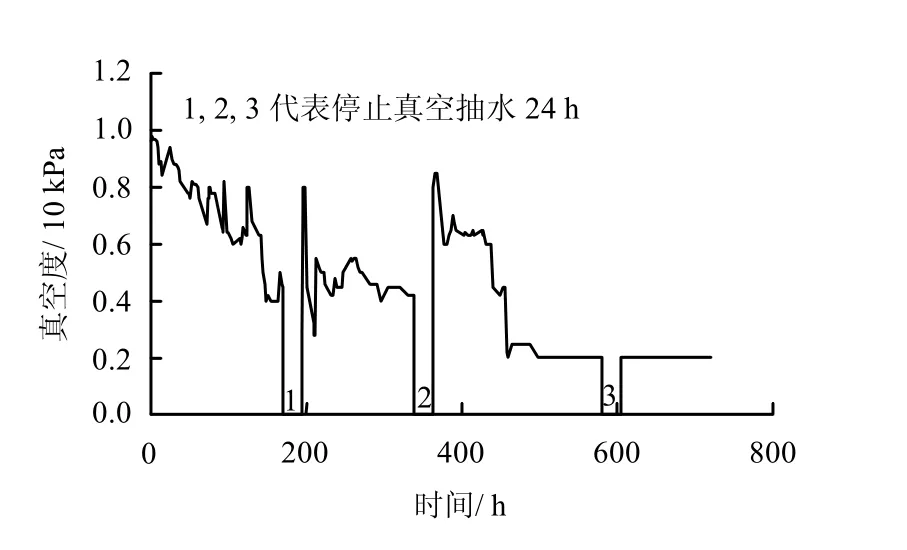
图2 试验过程中真空度随时间变化 Fig.2 Variation of vacuum degree along test process

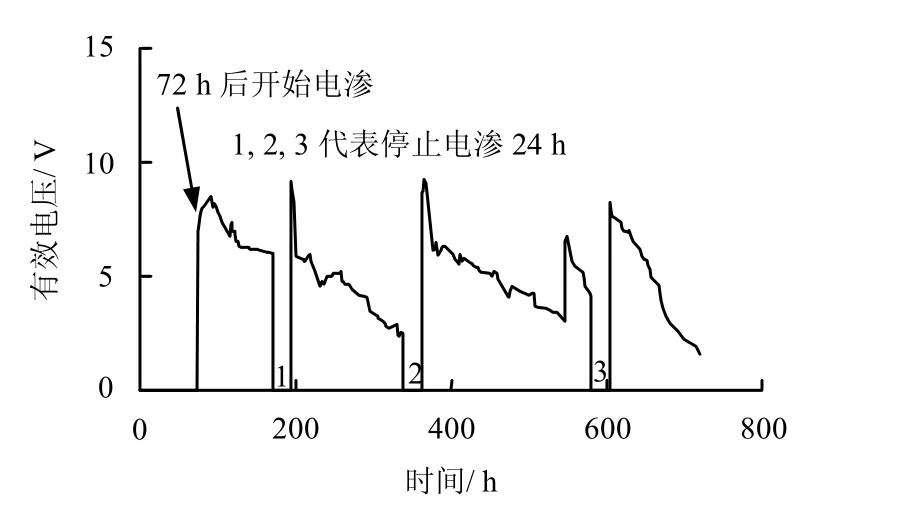
图3 试验过程中有效电压随时间变化 Fig.3 Variation of effective voltage along time of model test

图4 模型试验有限元网格 (单位：m) Fig.4 Finite element meshes of model test (unit: m)

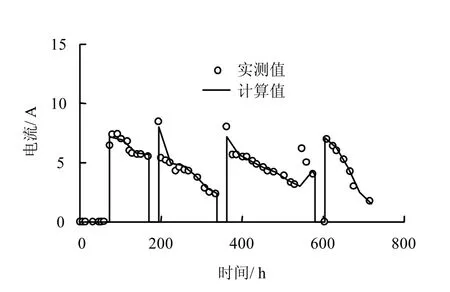
图5 电流的实测值与计算值比较 Fig.5 Comparison between calculated and measured current

图6 两极间土体电阻的实测值 Fig.6 The evolution of soil resistance between two poles

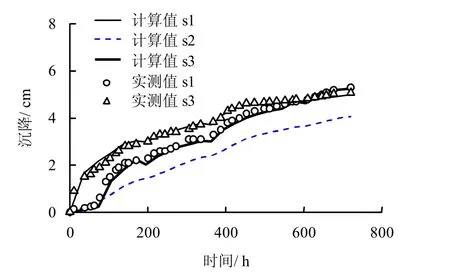
图7 表面沉降的实测值与计算值比较 Fig.7 Comparison between calculated and measured surface settlements

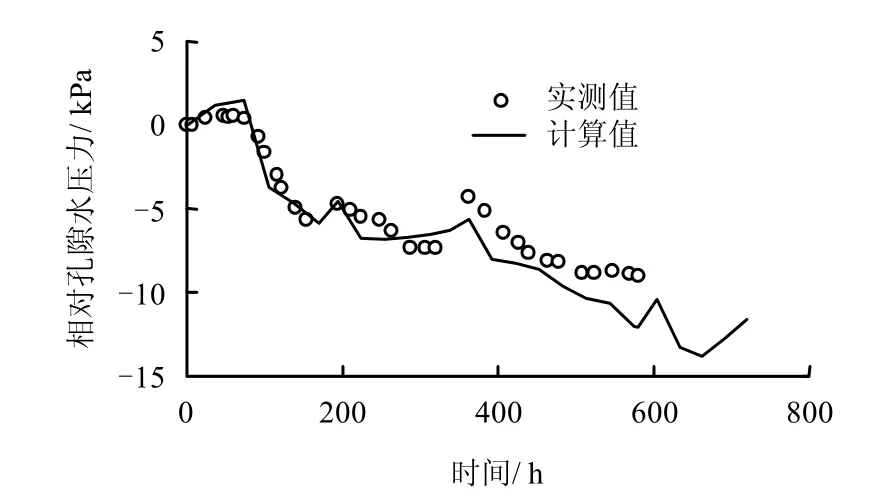
图8 点k1 处相对孔隙水压力实测值与计算值比较 Fig.8 Comparison between calculated and measured relative pore water pressure at node k1

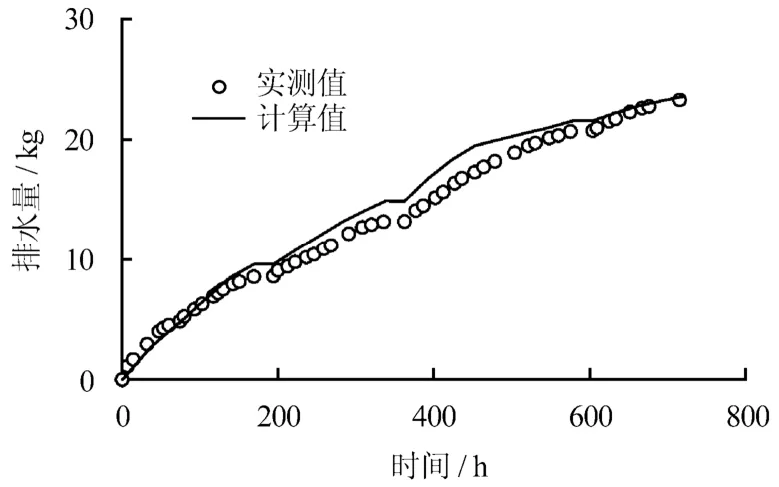
图9 试验总排水量的实测值与计算值比较 Fig.9 Comparison between calculated and measured overall drainage

图4 为模型试验的有限元网格。为简化网格，通过综合阴极导电特性和排水板的渗透特性，将其作为一种材料进行模拟。计算模型的边界条件为：模型箱底部及4 侧为已知位移边界，其中底部为固定边界，4 侧只约束其法向位移；由于土体表面铺有土工膜，除排水板顶部单元之外，模型的底部，顶部以及4 侧均为不排水边界，而排水板顶部设为水头边界，且该边界上的孔压约束值等于图2 所示的实测真空度；电极顶部单元为电势边界，其电势值输入如图3 所示。初始条件包括初始应力和初始水头，初始应力由土体自重决定；试验前土体处于完全饱和状态，初始水头为表面高度，等于0.5 m。计算所采用的参数包括土体、阳极以及阴极和排水板复合单元的电导率、电渗透系数、渗透系数、土水特征参数以及修正剑桥模型中的参数。其中土体 的电导率，土水特征关系以及力学本构关系如式（15）～（19）所示，其参数通过试验得到如下：σw=1.0 S/m， Keo=2.5×10-9m2/s·V，K=3.6，a= 2.051，b=5.531， p0=5 kPa，n=1.84， Srw=0.6，Ssw=1.0， Kw=1.95×106kPa， Ksw=2.5×10-9m/s，λ=4.179，κ=0.052，M=0.65，ν=0.3，e0=2.96。阳极以及阴极的电导率为5.0×106S/m，其电渗透系数相对土体可以忽略，取为1.0×10-20m2/ s·V；阳极和阴极的渗透系数也取为常数，由于阴极与排水板在模拟时作为一种材料处理，则将排水板的渗透系数等效到阴极后为2.0×10-4m/s，阳极的渗透系数远小于阴极，假设等于淤泥土的饱和渗透系数为2.5×10-9m/s；由于阴极和阳极的尺寸相对较小，对土体的变形影响可以忽略，因此，假设阴极和阳极采用的力学本构模型参数与土体一致。

4.3 计算结果分析

图5 为电渗过程中电流随时间变化的计算值与实测值的对比，两者十分接近。由图可知，电流随电渗时间的增长而减小，且其变化趋势与图3 中有效电压的变化趋势一致。这是由于电渗过程中阳极腐蚀以及阳极附近土体含水率急剧降低导致接触电阻增大，而由于土体初始含水率较高，且试验过程中平均含水率变化幅度较小，测得土体总电阻变化也较小，如图6 所示，由此说明了在该试验中有效电压的减小主要受接触电阻的影响。根据欧姆定律中电压和电流的关系可知，电流随电压的减小而减小；在每次间歇期之后通电，电流较通电前会有显著增大，这与间歇期土体中含水率、离子重分布以及累积电荷消散有关[17]。

图7 为试验过程中土体表面s1-s3 测点（参见图1）沉降的计算值与实测值比较。由于s2 处位移计失效，所以缺少了s2 处的实测值。由图可见，试验结束后，阴极表面沉降的计算值和实测值分别为5.07 cm 和4.98 cm，而阳极处表面沉降的计算值和实测值为5.29 cm 和5.24 cm，计算值与实测值基本吻合。在试验初始72 h 内，由于未开始电渗，阴极处沉降明显大于阳极；待土体中开始通电后，由于在电渗作用下阳极附近土体中的水分往阴极流动，引起阳极处的沉降速度加快，且试验结束后其最终沉降量大于阴极。

图8为k1处减去初始孔压值后的相对孔隙水压力的实测值与计算值的对比。在试验开始的72 h，由于曼德尔效应，k1 处孔压略有增大；电渗开始后，k1 处孔压逐渐减小且转变为负孔压，而在电渗间歇期，孔压略有增大。该现象说明了电渗能够使阳极附近产生负孔压，从而起到加固效果。

图9 为试验过程中排水总量的计算结果与实测结果的对比，两者也相当接近。由于试验的排水量与真空度、有效电压、土样和塑料排水板的渗透系数有关，是电渗法或电渗与其他工法联合的综合效果，图9 的计算结果表明了本文建立的电渗固结理论方程以及所采用的计算条件和参数的合理性。

图10 为计算得到的试验结束时刻对角线A-A剖面两极间土体中孔隙水压力、沉降、最大和最小有效主应力分布。可见，在电渗和真空排水联合作用下，土体中的最大负孔压分布在两极附近，而最小负孔压分布在两极中间略偏向阴极处。由于水流与土体介质的耦合关系，孔压减小，土体的有效应力增大，则沉降也增大。因此，孔压分布决定了土体中沉降和应力的分布，最大沉降发生在最大负孔压处，在阳极和阴极表面，表面沉降呈两极大、中间小的分布形式；土体中的应力分布同样呈两极大、中间小形式，说明了电渗和真空抽水均能使土体中产生负孔压，从而增大土体的有效应力，达到土体的加固效果。

图10 试验结束时刻A-A 剖面孔压、位移、 应力分布等值线 Fig.10 Isoline distribution of pore pressure, displacement, and stress in section A-A at the end of test

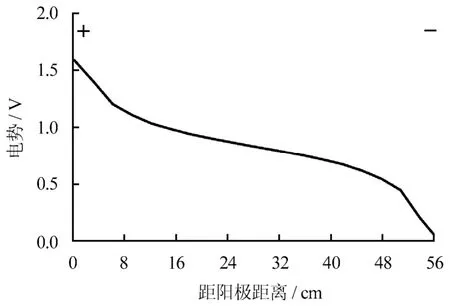
图11 试验300 h 后电势沿两极间分布情况 Fig.11 Potential distribution between anode and cathode after 300 hours test

图11 为试验结束时刻两极间土体中电势分布的计算结果。可见，两极间的电势并非呈直线分布，而是近似由3 条不同斜率的直线构成。靠近电极附 近的土体中电势梯度较大，而两极中间土体中的电势梯度较小。该分布规律与界面电阻有关，若电极与土体的接触面积增大，则界面电阻减小，电极附近土体中的电势梯度也将减小。该现象与文献[18]中的试验结果一致。

5 结 语

电渗固结问题是一个典型的非饱和土固结问题，它的解决必须充分考虑电场、渗流场以及应力场之间的相互作用关系。本文在非饱和土多孔介质力学理论的基础上，利用电荷守恒原理、质量守恒原理、应力平衡方程、达西定律以及欧姆定律，推导出基于三场耦合的电渗固结理论方程，提出了相应的数值解法，且自主开发了有限元程序，并对电渗联合真空排水的室内模型试验进行了数值模拟。算例表明，该模型的数值预测值与试验实测值无论在量值还是趋势上都吻合地较好，说明了本文所建立的电渗固结数值模型及其计算方法是正确、有效的，它不仅适用于工程中单独的电渗固结问题，还可以解决电渗与其他工法联合使用下的土体固结问题，从而为工程中涉及电渗固结的数值模拟提供了理论支持。由于电渗是一个涉及多个物理场相互作用的复杂问题，本文的工作尚处于初级阶段，还有待于深入研究。

[1] 汪闻韶. 汪闻韶院士土工问题论文选集[M]. 北京： 中国水利水电出版社， 1999.

[2] CASAGRANDE L. Electric-osmosis on soil[J]. Geotechnique， 1949， (1)： 159－177.

[3] CASAGRANDE L. Electro-osmotic stabilization of soils[J]. Journal of the Boston Society of Civil Engineers， 1952， (39)： 51－83.

[4] CASAGRANDE L. Stabilization of soils by means of electroosmosis-state-of-the-art[J]. Journal of the Boston Society of Civil Engineers， 1983， 69(2)： 255－302.

[5] MILLIGAN V. First application of electro-osmosis to improve friction pile capacity-three decades later[J]. Proceedings of the Institution of Civil Engineers, Geotechnical Engineering， 1995， 113：112－117.

[6] PERRY W. Electro-osmosis dewaters large foundation excavation[J]. Construction Methods and Equipment， 1963， 45(9)： 116－119.

[7] ESRIG M I. Pore pressures， consolidation and electrokinetics[J]. Journal of the Soil Mechanics and Foundations Division, ASCE， 1968， 94： 899－921.

[8] WAN T Y， MITCHELL J K. Electro-osmotic consolidation of soil[J]. Journal of the Geotechnical Engineering Division， 1976， 102(GTS)： 473－491.

[9] LEWIS W R， HUMPHESON C. Numerical analysis of electroosmotic flow in soils[J]. Journal of the SMFD, ASCE， 1973， 95 (SM4)： 603－616.

[10] 庄艳峰， 王钊， 林清. 电渗的能级梯度理论[J]. 哈尔滨工业大学学报， 2005， 37(2)： 283－286. ZHUANG Yan-feng， WANG Zhao， LIN Qing. Energy level gradient theory for electro-osmotic consolidation[J]. Journal of Harbin Institute of Technology， 2005， 37(2)： 283－286.

[11] 庄艳峰， 王钊. 电渗的电荷累积理论[J]. 岩土力学， 2005， 26(4)： 629－632. ZHUANG Yan-feng， WANG Zhao. Electric charge accumulation theory for electric- osmotic consolidation[J]. Rock and Soil Mechanics， 2005， 26(4)： 629－632.

[12] 苏金强， 王钊. 电渗的二维固结理论[J]. 岩土力学， 2004， 25(1)： 125－131. SU Jin-qiang， WANG Zhao. Theory of two-dimensional electric-osmotic consolidation of soils[J]. Rock and Soil Mechanics， 2004， 25(1)： 125－131.

[13] 李瑛， 龚晓南， 卢萌盟， 等. 堆载-电渗联合作用下的耦合固结理论[J]. 岩土工程学报， 2010， 32(1)： 77－81. LI Ying， GONG Xiao-nan， LU Meng-meng， et al. Coupling consolidation theory under combined action of load and electro-osmosis[J]. Chinese Journal of Geotechnical Engineering， 2010， 32(1)： 77－81.

[14] 刘国华， 王振宇， 黄建平. 土的电阻率特性及其工程应用研究[J]. 岩土工程学报， 2004， 26(1)： 83－87. LIU Guo-hua， WANG Zhen-yu， HUANG Jian-ping. Research on electrical resistivity feature of soil and it’ s application[J]. Chinese Journal of Geotechnical Engineering， 2004， 26(1)： 83－87.

[15] VAN GENUCHTEN T H M. A closed form equation predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal， 1980， 44：892－898.

[16] MUALEM Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research， 1976， 12(3)： 513－522.

[17] 汪俊波， 刘斯宏， 徐伟， 等. 电渗法处理大连大窖湾超软土室内试验[J]. 水运工程， 2010， 437(1)： 15－19.

[18] 庄艳峰， 王钊. 电渗固结中的界面电阻问题[J]. 岩土力学， 2004， 25(1)： 117－120. ZHUANG Yan-feng， WANG Zhao. Study on interface electric resistance of electroosmotic consolidation[J]. Rock and Soil Mechanics， 2004， 25(1)： 117－120.