裂隙网络无压渗流分析的初流量法

姚 池，姜清辉， ，叶祖洋，周创兵，

（1. 武汉大学 水资源与水电工程科学国家重点实验室，武汉 430072；2. 武汉大学 土木建筑工程学院，武汉 430072）

1 引 言

当前，描述裂隙岩体渗流的数学模型主要有3种方法，即等效连续介质模型、离散介质模型和双重介质模型。等效连续介质模型将裂隙岩体等效为连续体[1－3]，假定地下水在岩体中的流动服从Darcy 定律，然后运用经典的连续渗流理论进行分析，目前应用较为广泛，但该模型不能很好地反映空间结构面组合形成的裂隙网络的导水作用及优势流效应，在某些情况下数值模拟结果与实际出入很大。离散介质模型假定岩块不透水[4－6]，渗流只发生在岩体裂隙内，地下水通过相互连通的裂隙网络进行传导，岩体渗透特性受裂隙的迹长、走向、倾角和隙宽等参数控制，这种方法抓住了岩体中渗流主要受裂隙等结构面控制这一本质特征，具有广泛的应用前景，其主要缺点在于实际工程中裂隙网络资料不易获取，因此，常通过Monto-Carlo 法随机生成具有相同统计规律的裂隙网络来代替真实的裂隙网络。双重介质模型同时考虑了裂隙的强导水性、岩块的储水作用及岩块和裂隙的水量交换[7－8]，但该模型对裂隙系统的几何形态和空间分布存在较严格的假设，从而限制了其应用。

由于岩体本身赋存环境的复杂性，裂隙的发育极不规则，裂隙网络的几何构成往往非常复杂，导致渗流在岩体中的运动显示出明显的非均匀性和各向异性，很多情况下并不存在所谓的 REV（representative elementary volume）。此时，如用等效连续介质方法进行渗流分析实际上是不合适的，应该采用离散裂隙网络的模拟方法。总体上，相对基于多孔连续介质渗流分析方法，目前基于离散裂隙网络模型渗流问题研究相对较少，尤其对有自由面的裂隙网络渗流问题，国内外只有少数的几篇论文专门对其进行了探讨。Jing 等[9]利用DDA（discontinuous deformation analysis）形成的裂隙网络，采用剩余流量法求解裂隙网络自由面。王恩 志[10]借鉴初流量法的思想，提出了一种计算裂隙网络渗透自由面的迭代算法。柴军瑞等[11]提出含自由面岩体裂隙网络非线性渗流分析的传导矩阵调整法。由于上述方法主要借鉴求解连续介质渗流自由面的一些常用的直觉化求解方法，这些方法不具有严格的理论的基础，且因为没有解决溢出点的奇异性，计算过程中往往会出现数值的不稳定，对于含有大规模的复杂裂隙网络则难以收敛。

变分不等式方法是近年来求解连续介质无压渗流分析理论上的一个重要进展[12－13]，本文把单条裂隙概化为平行板模型，通过将Darcy 定律延拓到整个计算区域，定义了在整个区域上的非线性边值问题，并将潜在溢出面边界条件归纳为Signorini型边界条件，建立与PDE 提法等价的变分不等式(variational inequality， VI)提法，从而在理论上解决了出渗点的定位问题。通过采用有限元方法的线单元模拟裂隙，在有限元计算格式中，引入连续的罚Heaviside 函数，显著改善了离散裂隙网络渗流自由面迭代过程中的数值不稳定性。

2 有自由面裂隙网络渗流问题的描述

对于一个任意的二维裂隙网络，裂隙网络的连通性及裂隙的迹长、水力开度、位置等参数决定了地下水渗流在岩体中的分布，由于孤立的裂隙、只与一条裂隙相交的枝状裂隙及裂隙端部的独头不能作为渗流通道，对流场没有贡献，因此，在进行渗流分析前需对随机生成的裂隙进行必要的删减和截断，经过净化处理形成连通的裂隙网络，净化处理前后裂隙网络的对比可参见图1。

不失一般性，以图1 所示裂隙岩体边坡渗流问题为例，对于有自由面的无压渗流问题，区域Ω（ Ω=Ωw∪ Ωd）上的渗流实际上仅在自由面Γf以下的湿区Ωw中运动。在多孔连续介质渗流理论中，自由面是一个由计算域上压力水头为0 且法向流速为0 的点组成的连续曲面。而对于裂隙岩体而言，当忽略岩块渗流时，裂隙岩体的渗流是沿裂隙网络定向进行的，自由面在裂隙处表现为潜水面，依次连接裂隙处的潜水面位置可形成裂隙岩体渗流的自由面边界（见图1）。

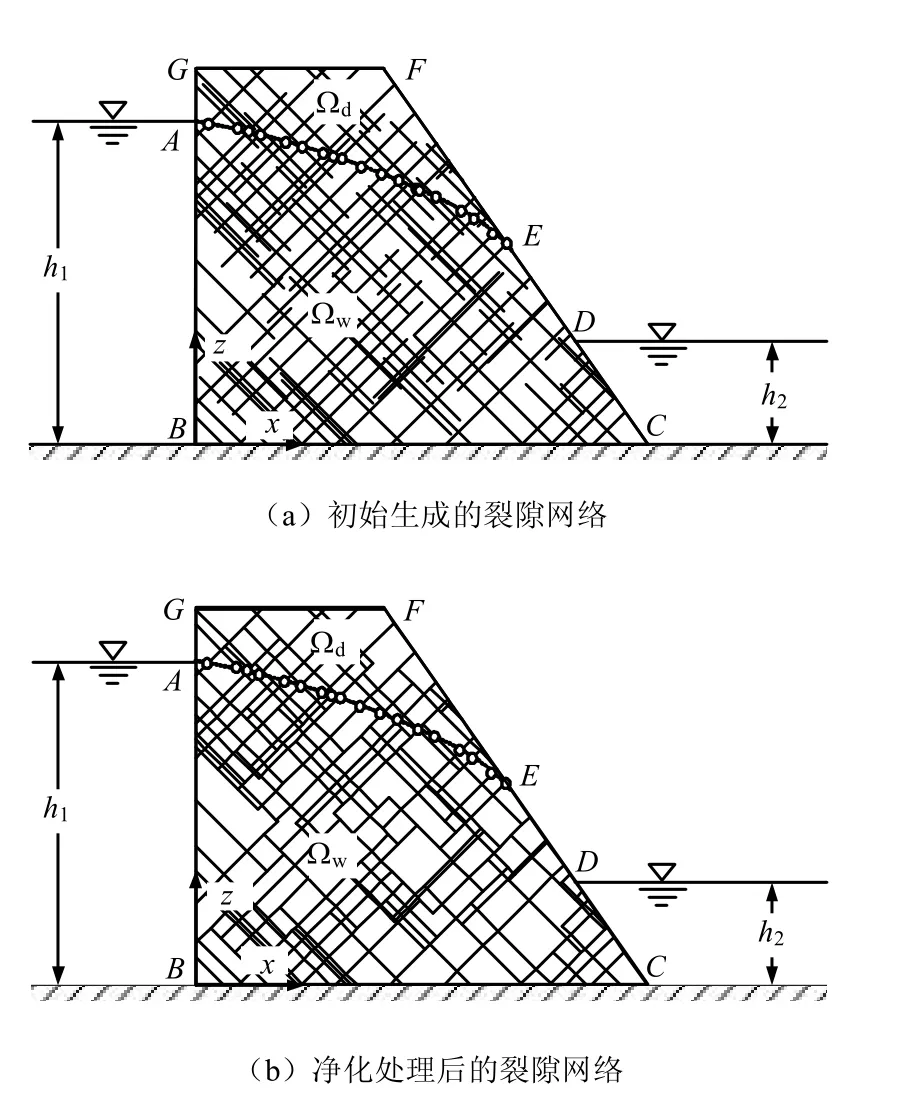
图1 裂隙岩体边坡渗流示意图 Fig.1 Schematic diagram of seepage flow through a fractured rock slope

假定边坡上游水位面位于A 点，下游水位面位于D 点，BC 为不透水边界，E 为溢出点，AE 为由裂隙处的潜水位构成的自由面。假定岩块不透水，地下水仅在自由面以下的裂隙网络湿区 wΩ 内产生流动。

裂隙网络湿区内任一点的总水头φ 可以定义为

式中：z 为垂直坐标分量；p 为裂隙水压力；wγ 为水的重度。

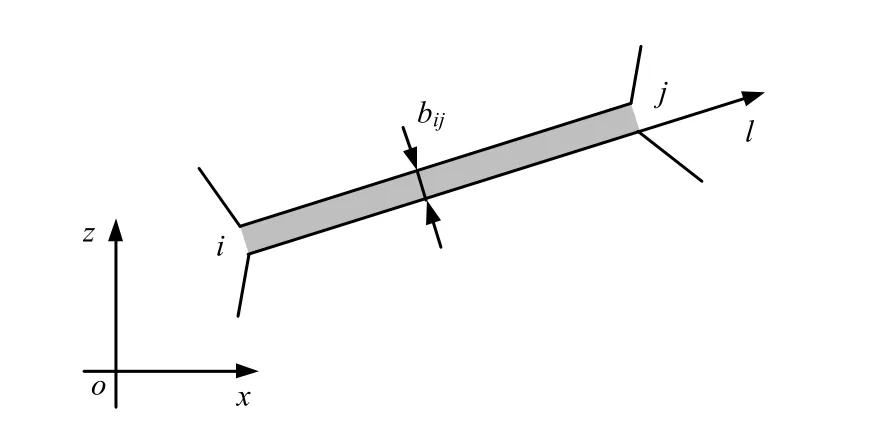
图2 裂隙ij 的局部坐标系 Fig.2 Local coordinate system of the fracture ij

把岩体中的裂隙概化为光滑平行板模型，在二维裂隙网络中，单个裂隙上的渗流是一维运动。如图1 裂隙ij 的局部坐标所示，对任意裂隙ij 建立局部坐标系，根据Darcy 定律，在裂隙ij 内的流速可表示为

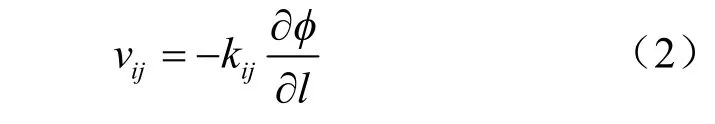
式中：ijk 为裂隙ij 的渗透系数。根据立方定理可得，

式中：g 为重力加速度；ijb 为裂隙ij 的隙宽；υ 为水的运动黏滞系数。

水在裂隙ij 内的流动应满足连续性方程：

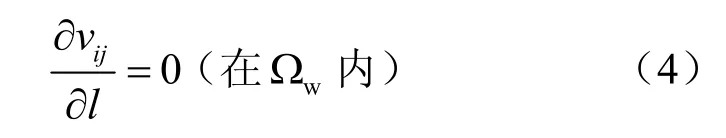
可知，ijv 在裂隙ij 上为常量。设有m 条裂隙汇聚于节点i，如图3 所示。由于节点i 本身不具备储存流体的能力，依据质量守恒原理，节点总流量的代数和为0，即

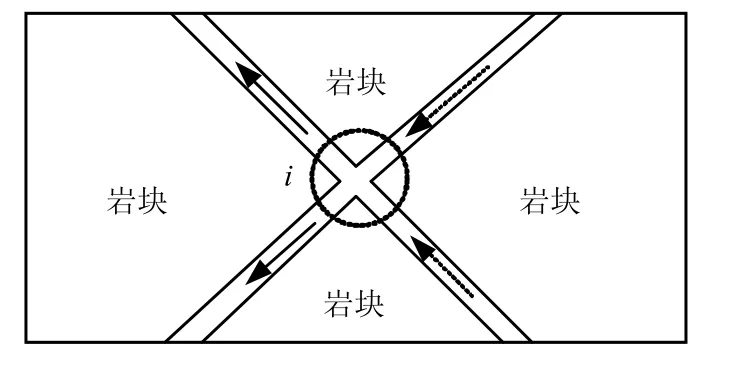
图3 通过节点i 的渗流量 Fig.3 Schematic diagram for flow distribution at fracture intersection.

水在裂隙网络湿区内的运动应满足连续性方程（4）和（5）以及下列边界条件： （1）水头边界条件

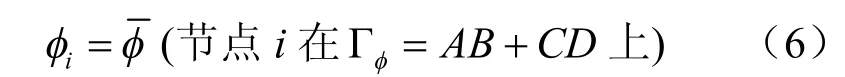
（2）流量边界条件

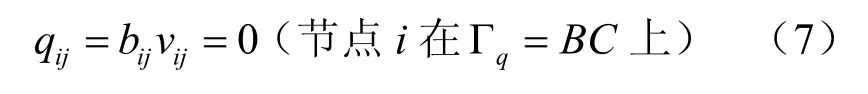
式中：Γq为隔水边界（规定流出为负）。

（3）自由面边界条件

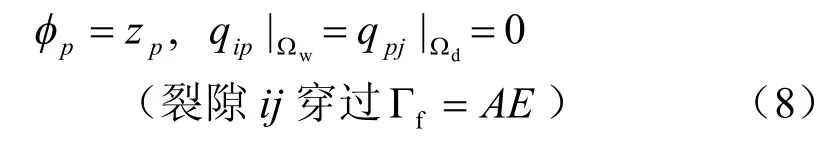
式中：p 为裂隙ij 与自由面的交点。

（4）出渗面边界条件

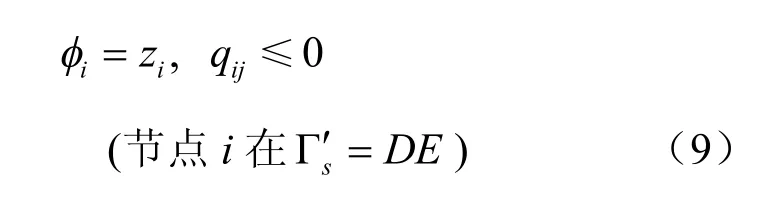
至此，给出了带自由面裂隙网络渗流问题的基本方程和边界条件，自由面fΓ 的位置事先未知，因此，确定其位置成了带自由面渗流分析的主要内容。

3 裂隙网络渗流全域上边值问题的PDE(partial differential equation)提法

为了建立全区域Ω 上的边值问题，借鉴初流量法的思想，将Darcy 定律延拓到整个区域

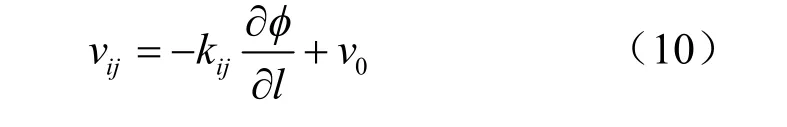
式中：0v 为初流速，初流速0v 的引入是为了抵消干区 dΩ 实际不存在的流速，其具体形式为

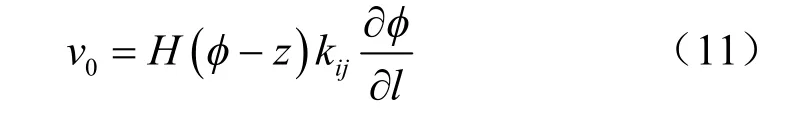
其中

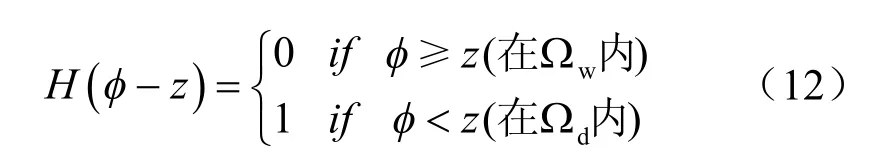
显然，(10)式中的 vij仍满足连续性方程。为了回避Ωw的不确定性，将构造一个定义在全域上的边值问题，该边值问题的基本方程由连续性方程、质量守恒方程和广义Darcy 定律构成，水头边界条件和流量边界条件保持不变。剩下的边界AGFD 为Signorini 型互补边界条件，

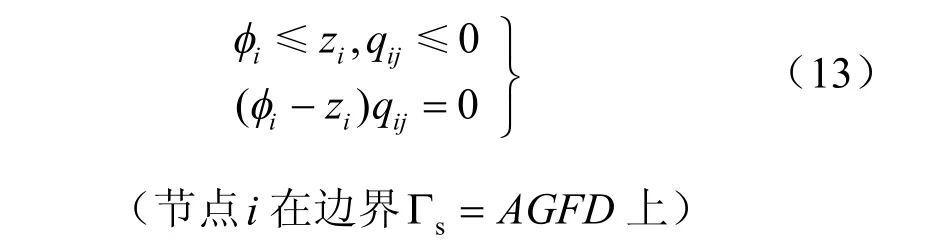
综上所述，定义在整个裂隙网络上边值问题的提法是：求函数φ，使其满足控制方程（4）和（5）、外部边界条件（6）、（7）和式(13)以及内部自由面边界条件式（8）。

4 裂隙网络渗流全域上边值问题的VI 提法

上述PDE 提法中含有未知的内部自由边界fΓ和潜在的溢出面Signorini型互补条件，数值求解中选取其试探函数非常困难。通过建立与PDE 提法等价的变分不等式(VI)提法，使得自由边界fΓ 以及潜在溢出边界上的互补条件转化为自然边界条件，从而大大减小数值求解的难度，并改善数值计算的收敛性和稳定性。

定义试探函数集VIΦ 为

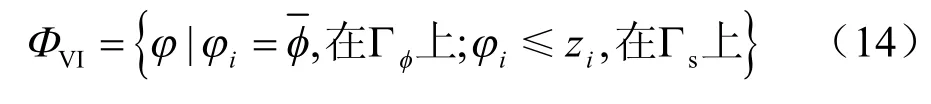
则在数学上与上述PDE 提法完全等价的变分不等式(VI)提法可表述为：在ΦVI中求一函数φ，使得对∀ψ ∈ΦVI，都有如下不等式成立

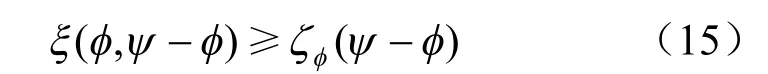
其中， ξ (φ ，ψ - φ)和 ζφ(ψ - φ)的形式为

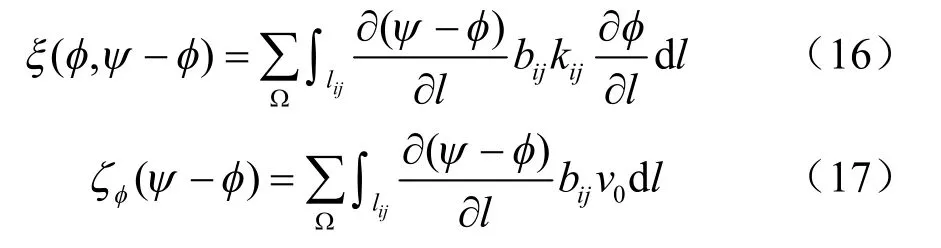
为了完成两种提法的等价性证明，首先利用分部积分展开式 ξ (φ ，ψ - φ ) - ζφ(ψ - φ)：

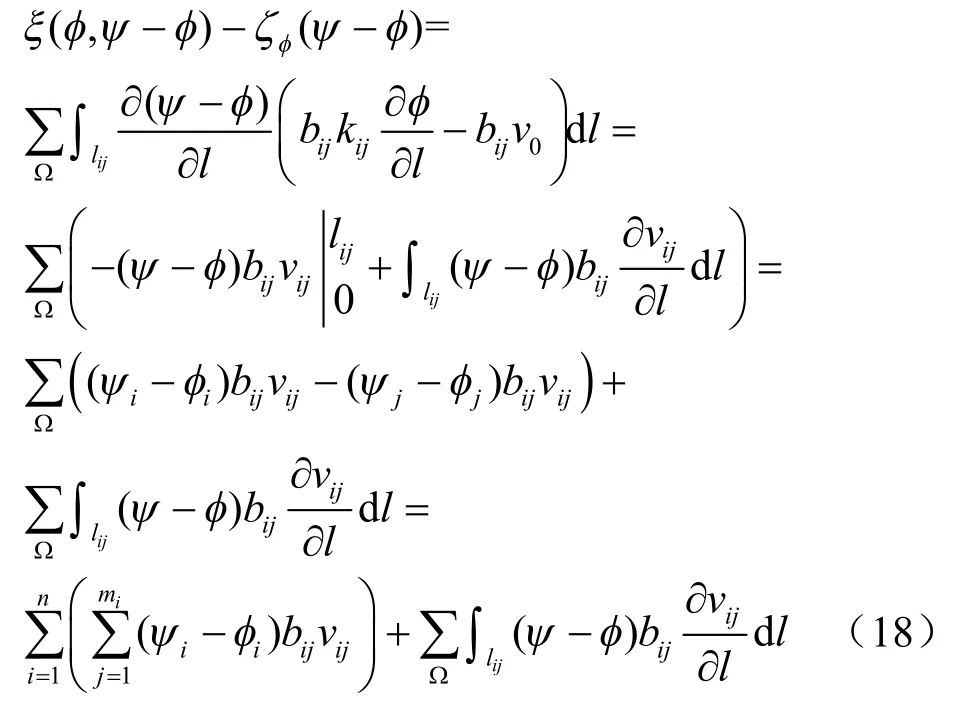
式中：n 为整个区域所有裂隙节点的总数；im 为汇聚于i 节点的裂隙条数。

4.1 PDE 提法⇒VI 提法

如果φ 是PDE 提法的解，将连续性方程式（4）和（5），外部边界条件（6）、（7）和（13）代入式（18），并注意到条件式（14），得

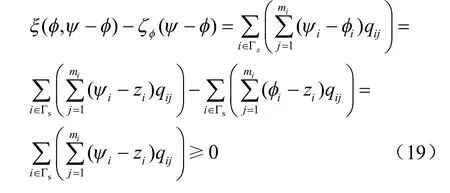
因此，φ 也是VI 提法的解。

4.2 VI 提法⇒PDE 提法

假定φ 是变分(VI)提法的解， ∀ψ ∈ΦVI都满足式（18）。分别取ψ = φ + θ1和ψ = φ - θ1，其中θ1为在所有裂隙节点上等于0 的任意函数，可以得到连续性方程为

因此，式（18）可以简化为

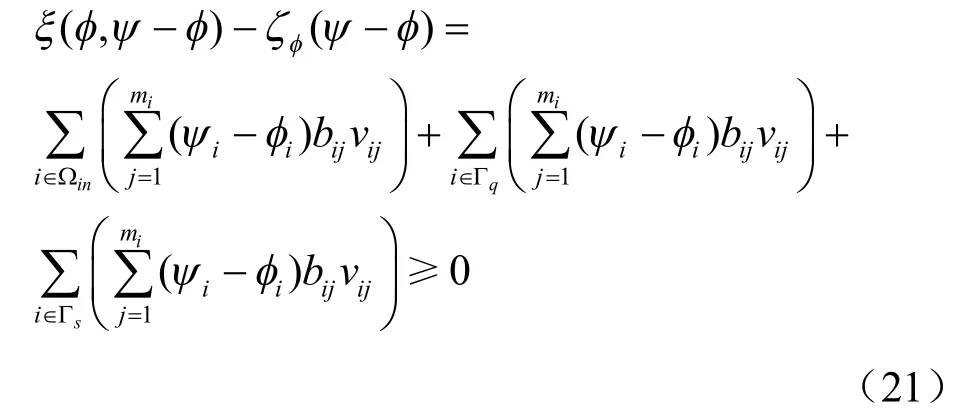
在式（21）中分别取ψ = φ + θ2，ψ = φ - θ2，其中θ2为在 Γφ、 Γq和 Γs边界上裂隙节点等于0 的任意函数，可以得到内部任意节点上的质量守恒方程为

因而式（21）可以简化为

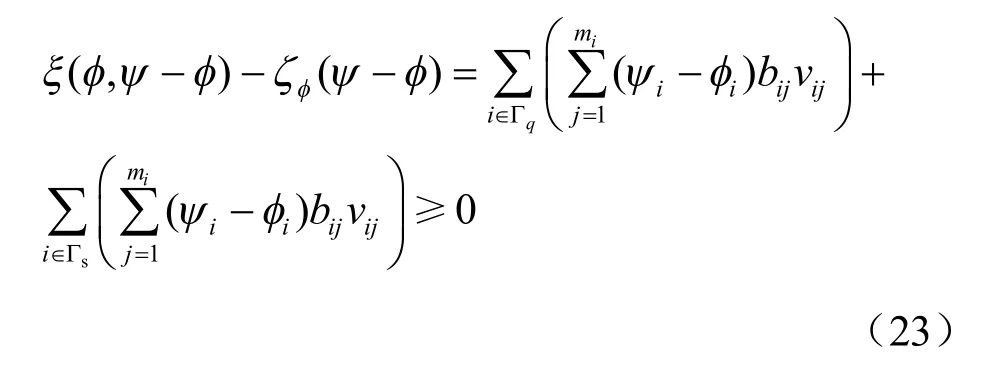
对式（23）分别取ψ = φ + θ3，ψ = φ - θ3，其中 θ3为在 Γφ和 Γs边界上裂隙节点等于0 的任意函数，可以得到 Γq上裂隙节点的流量边界条件为

因此，式（23）可以进一步简化为

考虑到上式等号右边的第二项为一常数，要使不等式对于 ∀ψ ∈ΦIV都成立，则等号右边的第一项必须非负，即

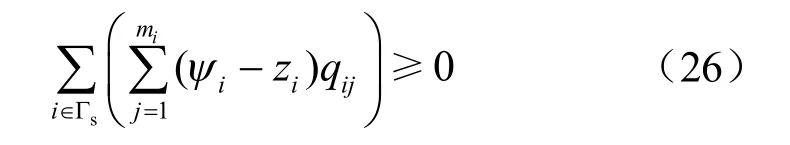
考虑到式（14），很明显可以得到

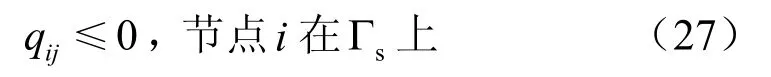
在式（25）中当然也可以取 zψ= ，如此就有

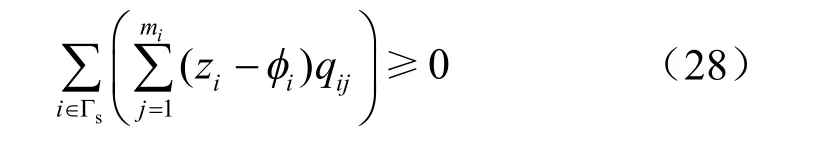
由式（27）、（28）以及在sΓ 上iizφ ≤ ，可得sΓ 上的互补条件为

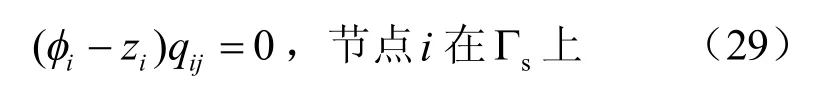
为导出内部自由面fΓ 边界条件，将式（18）中的Ω 表示成 wΩ 和 dΩ 上的积分之和为

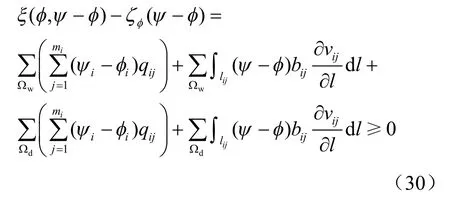
利用上面已经导出的条件，可得对于∀ψ ∈ΦIV，

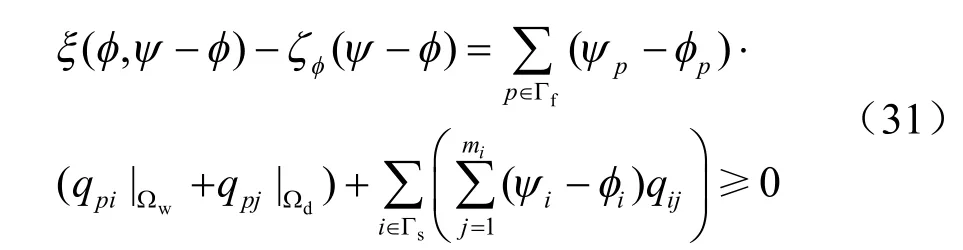
分别取ψ = φ + θ4和ψ = φ - θ4，θ4为在 Γφ和 Γs边界上裂隙节点等于0 的任意函数，如此可得：

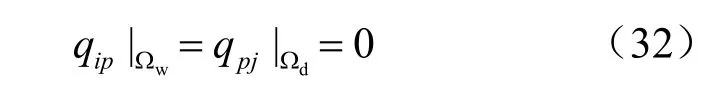
至此，已经导出了PDE 提法中的全部方程及边界条件。

5 有限元数值求解格式

5.1 自适应罚Heaviside 函数

尽管可以对式（15）进行离散来求其数值解，但由于其中的Heaviside 函数的不连续性，将导致数值不稳定性，主要原因是Heaviside 函数为非连续的阶梯式函数，在对单元积分时会造成数值的跳跃。为避免这种数值跳跃，采用自适应罚Heaviside 函数来代替Heaviside 函数，其具体表达式为

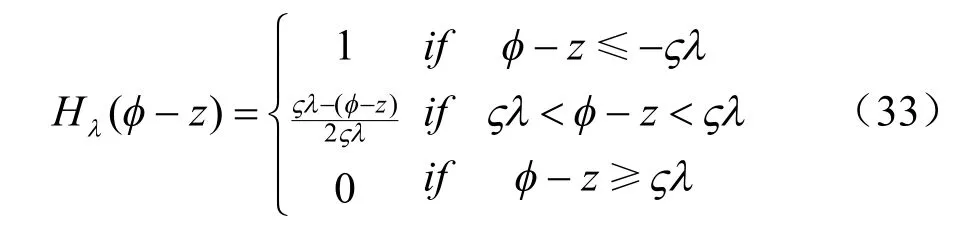
式中：2λ 为自由面附近由干区到湿区的过渡层厚度，在计算中可以取为穿过自由面裂隙平均长度的1/10；ς 为自适应放大系数，为获得较好的收敛性，可适当调整其大小。

5.2 有限元求解格式

将裂隙网络中的单条裂隙看成是有限元中的线单元，单元节点即为裂隙的两个端点，对裂隙ij，其上任意一点的水头可以用节点i、j 的水头表示为

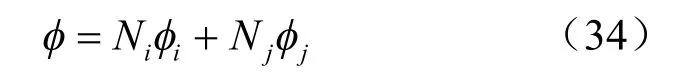
式中： Ni、 Nj为形函数， Ni= 1 -l /lij， Nj= l /lij。

经过有限元近似后得到的变分不等式提法为：寻找一水头向量 φr+1∈I，对于 ∀ψ ∈，都有以下不等式成立，

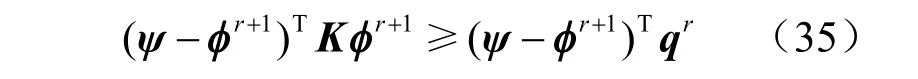
其中

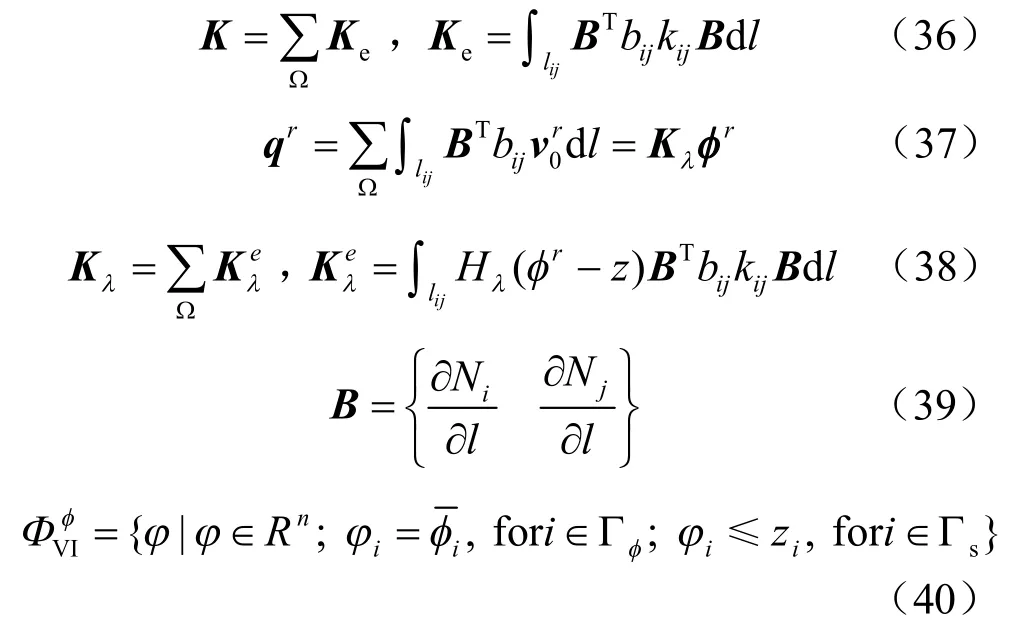
式中：n 表示整个区域所有裂隙节点的总数；r 和r+ 1表示迭代次数。求解离散形式的变分不等式的算法有很多，本文选用Zheng 所建议的算法[14]。

5.3 迭代过程

Signorini 型变分不等式方法求解有自由面的渗流问题时，溢出边界的判断和自由面的迭代是同时进行的。为表述方便，将节点总集N 划分为4 个子集：

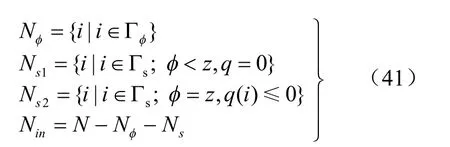
式中：inN 为整个裂隙网络区域内部节点集合。

基于上述离散型VI 提法的无压渗流分析方法的有限元迭代算法如下：

步骤1：构造总体渗透传导矩阵K ，设对边界Γs上的 ∀i，都有 i ∈。求解方程 Kφ1=0，得到φ1。

步骤2：令 1r=

（3）如果 |φr+1- φr||＜ ε|| φr||，则转入步骤3，否则令 r = r+ 1，转入（1）。

步骤3：令φ =φr，计算结束。

6 算 例

基于本文所建立的裂隙网络无压渗流分析的变分不等式提法，采用Visual C++语言和面向对象的程序设计方法，研制开发了相应的计算程序FracSeepage，并用多个算例对程序进行了考察，验证了程序的有效性和鲁棒性。

6.1 均质矩形坝的渗流分析

如图4 所示，有一均质矩形坝，坝高为12 m，宽为10 m，底部边界隔水，上游水位为10 m，下游水位为2 m。采用间距为0.2 m，有着常水力开度的两组正交裂隙形成的裂隙网络来模拟均质矩形坝的渗流，则裂隙的等效隙宽可以表示为

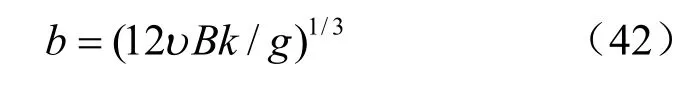
式中：k 为坝体材料的渗透系数，B 为裂隙间距。计算中选取均质坝体的渗透系数 k = 4.13× 10-3mm/s，则裂隙的等效隙宽 b= 0.1 mm。

对于该算例，图4 给出了自由面的经验解及裂隙网络渗流数值计算结果，其中经验解为

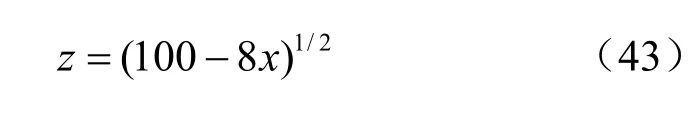
对于渗流溢出点，经验解为z=4.47 m，数值解为z=4.27 m。表明数值解与经验解较为吻合，但数值解的自由面降落略大于经验解。

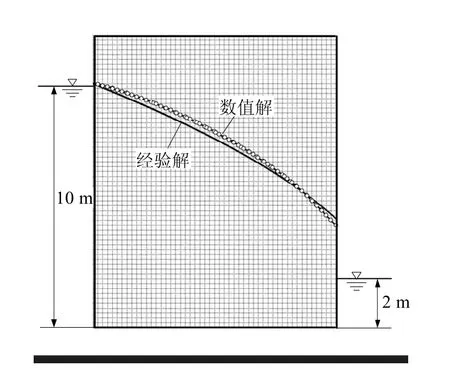
图4 均质矩形坝渗流自由面位置的比较 Fig.4 Comparison of locations of the free surface from different approaches

根据Dupuit 假定，均质坝体渗流的总流量可以表示为

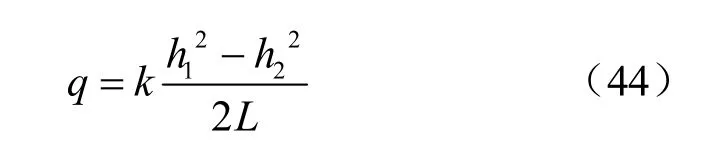
式中：1h 和2h 分别表示上下游水位，L 表示坝体宽度。

采用 Dupuit 公式得到坝体渗流量为1.98 × 10-5m2/s，基于裂隙网络渗流分析的数值解为 1.95 × 10-5m2/s，两者误差仅为1.79%，表明数值解的计算结果是合理可靠的。

6.2 复杂裂隙网络渗流分析

为了研究裂隙岩体的渗透特性和水力耦合特性， 国 际 合 作 项 目 Decovalex[15]第 5 期（Decovalex-2011）的Task 提供了一个含有7 797裂隙、29 814 个节点的复杂裂隙网络模型即DFN（discrete fracture network），如图5 所示。产生该DFN 模型的裂隙参数来自英国Sellafield 地区的现场地质测量[16]，发育有4 组裂隙，裂隙产状服从Fisher 分布，裂隙迹长服从负指数分布，表1 给出了裂隙的几何参数及统计分布规律。

图5 裂隙网络模型 Fig.5 Geometry of fracture system in the DFN model

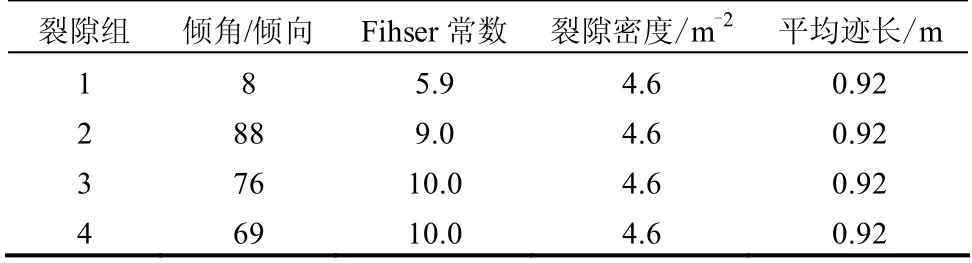
表1 裂隙几何参数 Table 1 Fracture parameters used for DFN generation

本文采用该DFN 模型进行裂隙网络无压渗流分析，假定模型左侧水头边界为10 m，右侧水头边界为20 m，底部为不透水边界。为了分析裂隙的水力开度对裂隙网络渗流的影响，计算考虑了两种情况：（1）所有裂隙的隙宽为常数65 um；（2）裂隙的隙宽服从对数正态分布且裂隙迹长与隙宽相关，两者的关系函数为[17]

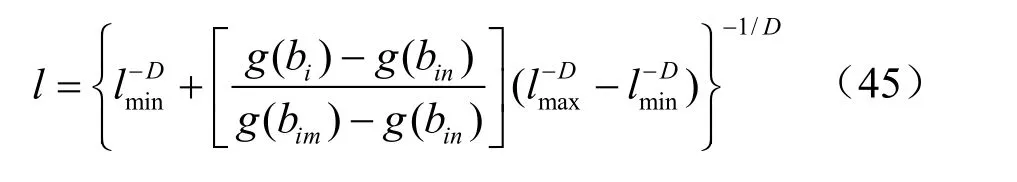
式中：minl 和maxl 为最小和最大的裂隙迹长；D 为分形维数；g 为截断误差函数；imb 和inb 为裂隙隙宽的上、下限。

图6给出了DFN模型在两种不同水力开度分布条件下裂隙网络内的流量分布及自由面位置，图7给出了模型左边界裂隙出口的流量分布。从图6、7可以看出，对于所有裂隙隙宽为常水力开度的情况，裂隙网络内部以及裂隙在下游边界出口的流量分布相对比较均匀，而且自由面形状变化平缓；对于裂隙隙宽服从对数正态分布且与迹长相关的情况，裂隙网络内部及出口的流量分布主要由隙宽较大、迹长较长的裂隙所控制，优势流的效应比较明显，充分反映了长大裂隙的导水作用。同时，受裂隙隙宽随机分布影响，自由面形状在局部起伏较大。图8还给出了裂隙网络内部水头等势线的分布，可以看出，水头自裂隙网络右侧向左侧随整体水流方向逐步递减，与连续介质渗流规律基本一致。

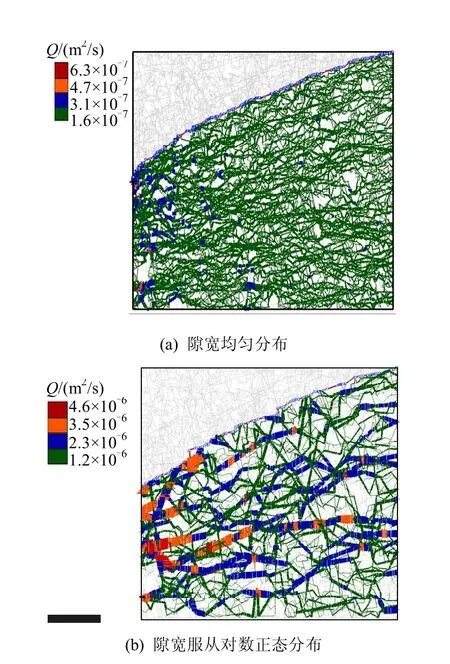
图6 裂隙网络内部流量分布 Fig.6 Flow rates distribution in the DFN model

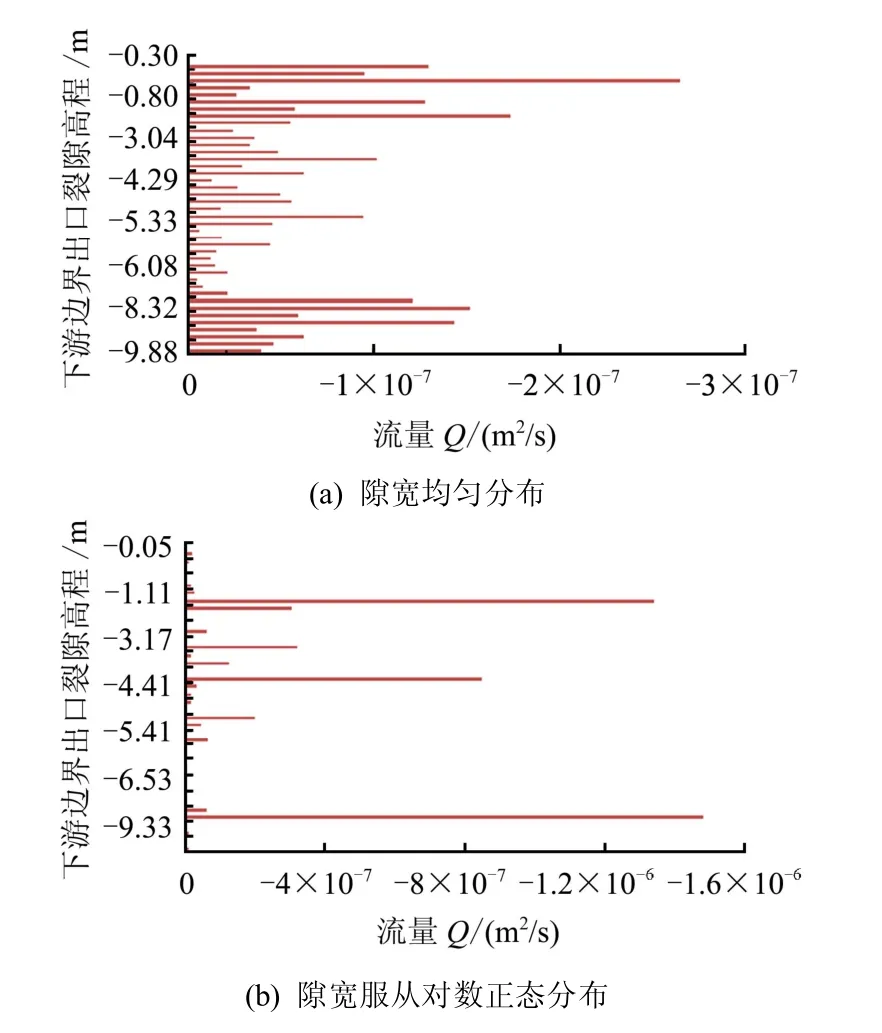
图7 下游边界出口裂隙流量分布 Fig.7 Flow rates distribution in each fracture intersecting the left vertical boundary of the model

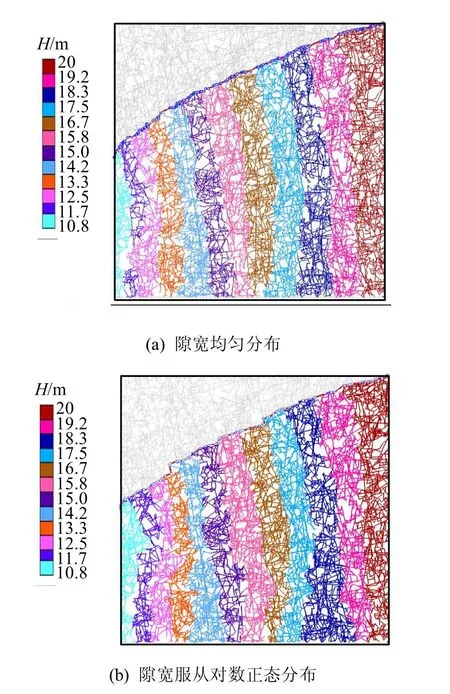
图8 裂隙网络水头等势线分布 Fig.8 The water head contours in unit of m

7 结 论

（1）引入初流速来抵消在裂隙网络干区实际不存在的流速，将Darcy 定律扩展到整个区域，定义了在整个区域上的非线性边值问题，并将潜在溢出面边界条件归纳为Signorini 型边界条件，建立等价的变分不等式提法，从而在理论上解决了出渗点的定位问题。

（2）通过使用连续型的自适应Heaviside 函数 代替阶梯型的Heaviside 函数，避免了在自由面附近由干区到湿区的过渡区域进行积分时形成的数值跳跃，从而显著提高了在精确定位自由面和溢出点的数值求解过程中的稳定性和程序的鲁棒性。

（3）来自均质坝体和Decovalex Task 的复杂裂隙网络算例验证了本文算法的有效性，同时表明，该算法对复杂裂隙网络具有良好的适应性，并能反映裂隙网络渗流的结构特征。

[1] 张有天， 陈平， 王镭. 有自由面渗流分析的初流量法[J]. 水利学报， 1988，8(1)： 18－26. ZHANG You-tian， CHEN Ping， WANG Lei. Initial flow method for seepage analysis with free surface[J]. Journal of Hydraulic Engineering， 1988， 8(1)： 18－26.

[2] 毛昶熙. 渗流计算分析与控制[M]. 北京： 中国水利水电出版社， 2003.

[3] LONG J C S， REMER J S， WILSON C R， et al. Porous media equivalents for networks of discontinuous fractures[J]. Water Resources Research， 1982， 18(3)： 645－658.

[4] 毛昶熙， 陈平， 李祖贻， 等. 裂隙岩体渗流计算方法研究[J]. 岩土工程学报， 1991， 13(6)： 1－10. MAO Chang-xi， CHEN Ping， LI Zu-yi， et al. Research on fractured rock mass seepage calculation method[J]. Chinese Journal of Geotechnical Engineering， 1991， 13(6)： 1－10.

[5] LONG J C S， GILMOUR P， WITHERSPOON P A. A method for steady fluid flow in random three-dimensional networks of disc-shaped fractures[J]. Water Resources Research， 1985， 21(8)： 1105－1115.

[6] 张奇华， 邬爱清. 三维任意裂隙网络渗流及其解法[J]. 岩石力学与工程学报， 2010， 29(4)： 720－730. ZHANG Qi-hua， WU Ai-qing. Three-dimensional arbitrary fracture network seepage model and solution[J]. Chinese Journal of Rock Mechanics and Engineering， 2010， 29(4)： 720－730.

[7] 王嫒， 速宝玉. 裂隙岩体渗流模型综述[J]. 水科学进展， 1996， 7(3)： 276－282. WANG Yuan， SU Bao-yu. Comment on the models of seepage flow in fractured rock masses[J]. Advances in Water Science， 1996， 7(3)： 276－282.

[8] BARENBLATT G I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks[J]. Journal of Applied Mathematical Mechanics， 1960， 24 (5)： 1286－1303.

[9] JING L， MA Y， FANG Z. Modeling of fluid flow and solid deformation for fractured rocks with discontinuous deformation analysis (DDA) method[J]. International Journal of Rock Mechanics and Mining Sciences， 2001， 38(3)： 343－355.

[10] 王恩志. 剖面二维裂隙网络渗流计算方法[J]. 水文地质工程地质， 1993， 20(4)： 27－29. WANG En-zhi. Seepage calculation method in fissure networks on vertical section[J]. Hydrogeology & Engineering Geology， 1993， 20(4)： 27－29.

[11] 柴军瑞， 仵彦卿. 岩体裂隙网络渗流自由面的确定方法[J]. 工程勘察， 2000， 1： 23－24. CHAI Jun-rui， WU Yan-qing. The method for determination of the position of free surface in fractured rock masses[J]. Geotechnical Investigation & Surveying， 2000， 1： 23－24.

[12] ZHENG H. A new formulation of Signorini’s type for seepage problems with free surfaces[J]. International Journal for Numerical Methods in Engineering， 2005， 64(1)： 1－16.

[13] CHEN Y， ZHOU C， ZHENG H. A numerical solution to seepage problems with complex drainage systems[J]. Computers and Geotechnics， 2008， 35(3)： 383－393.

[14] ZHENG T S， LI L， XU Q Y. An iterative method for the discrete problems of a class of elliptical variational inequalities[J]. Applied Mathematics and Mechanics， 1995， 16(4)： 351－358.

[15] NIRE X. Evaluation of heterogeneity and scaling of fractures in the Borrowdale Volcanic Group in the Sellafield area[R]. UK： [s. n.]， 1997.

[16] JING L， TSANG C F， STEPHANSSON O. DECOVALEX－An international cooperative research project on mathematical models of coupled THM processes for safety analysis of radioactive waste repositories[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts， 1995， 32(5)： 389－398.

[17] ALIREZA B， LANRU J. Hydraulic properties of fractured rock masses with correlated fracture length and aperture[J]. International Journal of Rock Mechanics and Mining Sciences， 2007， 44(5)： 704－719.