基于混合粒子群算法和能量法主动土压力计算
陈昌富,唐仁华,梁冠亭
(湖南大学 岩土工程研究所,长沙 410082)
1 引 言
自Terzaghi[1]使用对数螺线滑动面模型求解挡土墙土压力后,此模型经历了几十年试验和实践的考证,被普遍认为是最接近实际的破坏机构[2]。Chen[3]较早地系统研究了极限分析法在土压力中的应用,随后许多学者运用塑性极限上限方法来计算土压力,取得了较多成果。范文等[4]和杨建民[5]利用多三角形破坏机构,分别基于统一强度理论和非线性强度准则求得了土压力的上限解。杨小礼[6]运用非线性强度准则分析了墙后填土面水平时动、静主动土压力上限解。Chen[3]分别采用6 种破坏机构结合最速下降法求得了土压力系数,其中2 条直线中间夹对数螺线破坏机构的计算结果与广泛接受的Sokoloskii[7]解误差最小,Chen 认为,是对数螺线夹层起到了关键作用。但上述机构假定对数螺线的中心固定于坡顶不变,而实际情况并非如此。本文采用接近实际情况的单纯对数螺线滑动面破坏机构,不约束对数螺线中心的位置,推导出土压力及其系数计算公式,然后运用基于自然选择的混合粒子群算法对最危险滑动面进行全局搜索并计算主动土压力,最后将本文方法计算结果与已有解答和实测值进行对比分析。
2 基于能量法和对数螺线滑裂面的主动土压力计算
能量法计算土压力需用到以下两个结论[8]:
(1)流动法则:土体处于塑性流动或剪切滑动状态时,滑动面上任一点的应变速度矢量v 与该点处的滑动线成φ 角。
(2)土体在塑性流动中的能量消散为cvcosφ。c、φ 分别为土体的黏聚力和内摩擦角。
如图1 所示的挡土墙,墙高为H,墙背与水平面成β 角,墙后填土与水平面成α 角。填土上作用均布荷载q。以坡顶处A 点为坐标原点,向左和向上分别定为x,y 坐标轴的正方向。

图1 对数螺线滑动面计算图 Fig.1 Calculation diagram of log-spiral sliding surface
假定滑动面为通过墙底的对数螺线滑动面,其动径方程为
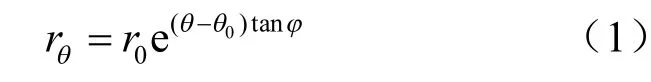
式中:rθ为0r 绕中心旋转θ 角后的动径长度(m);0θ为0r 与水平面的夹角(°);0r 为对数螺线通过边坡的旋入点到螺线中心的长度(m)。
当θ =hθ 时,
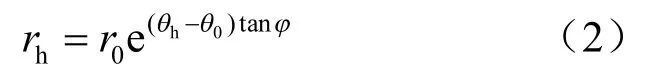
式中:hr 为对数螺线通过边坡的旋出点至螺线中心的长度(m);hθ 为hr 与水平面的夹角(°)。
过O 点作AB 的平行线与CA 的延长线交与点E;作AC 的平行线与BA 的延长线交于点F,则

由式(3)可以推出

此外,对数螺线参数还满足式(5)中的几何关系
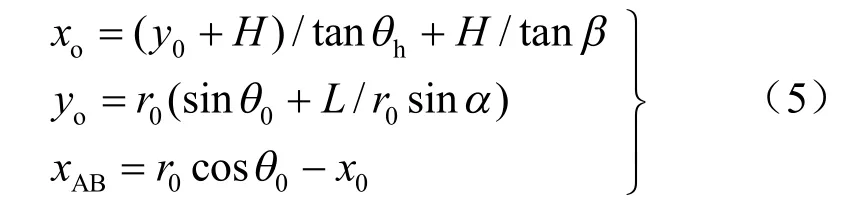
式中:xo为对数螺线中心横坐标(m);yo为对数螺线中心纵坐标(m);L 为滑裂面起点到坡顶的距离;xAB为L 在x 轴负方向的投影。
作用在滑动土体上的外力有均布荷载载q,滑动土体的重力W 已及挡土墙对滑动土体的反作用力p。假设滑动土体绕对数螺线中心产生微小的角速度ω,由假定的对数螺线方程可知,螺线上每点的切线方向与动径成(π/2 φ+ )角,结合流动法则,则滑动面上每点的应变速度方向均与动径垂直,即
如图2、3 所示,由于超载和重力的方向都是竖直向下,故其与速度方向夹角等于动径与水平线的夹角。即超载或重力做的功等于力与角速度ω 的乘积,再乘以超载或者单元土体形心到对数螺线中心O 点的水平距离。
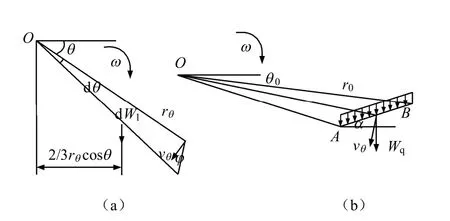
图2 滑体发生微小转动计算图 Fig.2 Calculation diagram of small rotation on slide soil
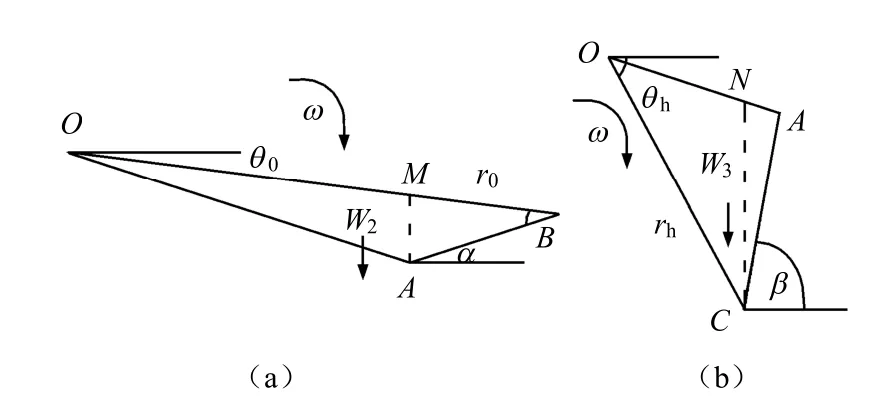
图3 滑体发生微小转动计算图 Fig.3 Calculation diagram of small rotation on slide soil
超载q 所作的功为

如图4 所示,滑动土体重力作的功可由叠加法求出。以W1表示OBC 对假定转动中心O 作的功,W2表示OAB 对假定转动中心O 作的功,W3表示OAC 对假定转动中心O 作的功。OAB 形心到O 点的水平距离可由OAM 与ABM 组合求出,OAC 形心到O 点的水平距离可由OCN 与ACN 组合求出。则W1,W2,W3分别为


沿对数螺线微分长度 rθdθ / cosφ 上的消耗功为( rθdθ / cosφ ) cv cosφ = crθvd θ,内部总消耗功为
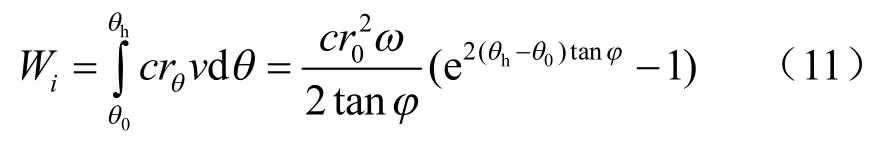

图4 AC 面上单元土体速度矢量图 Fig.4 Soil element’s velocity vector on surface AC
如图4(a),由余弦定理知


由正弦定理知
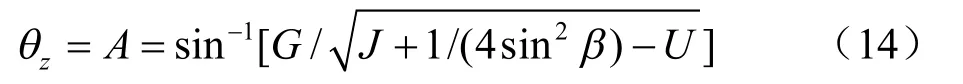
式 中:A=sin-1[ H sin(β + θh)/(2 ozsin β)];G = sin(β +θh)/(2sin β);J = ( r0/ H )2e2(θh-θ0)tanφ;U=cos(β +θ )/ H sin β。 h
图4(b)右为AC 面上单元土体速度矢量合成图,可见其平均速度即为中点Z 处的速度。土压力合力P 与墙面法线夹角为δ (外摩擦角),位于法线下方,与Z 点速度方向夹角为π-(hθ -zθ )-β -δ ,则挡土墙对AC 面土体的反力所做功为
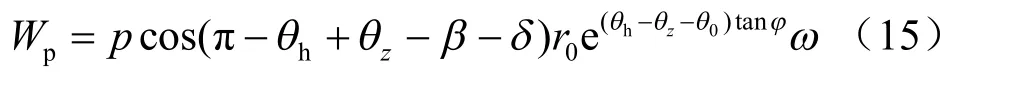
由于挡土墙对土体的反力与土体的应变速率方向相反,故其所做之功为负值。由外力作的功等于土体内部消耗的能量,消去角速度可得:
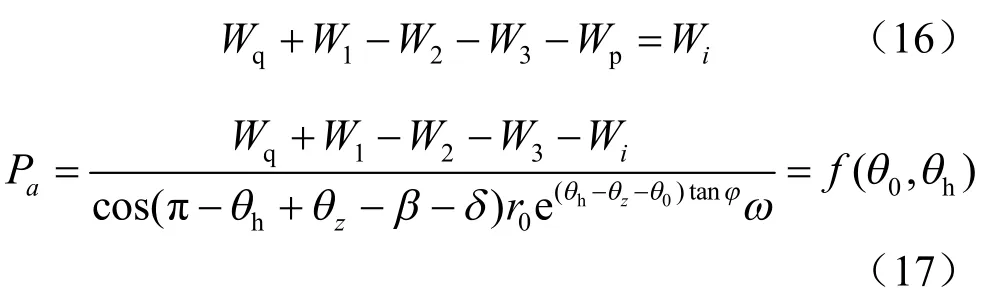
式(17)即为主动土压力计算公式。显然,这是一个二元函数的极值问题,对于主动土压力,应取其最大值。
特别地,当α =0°、β =90°,即墙背竖直、墙后填土面水平时,整理公式后可得:
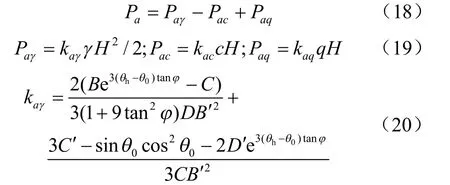
式中:

不同深度处的主动土压力强度pH为
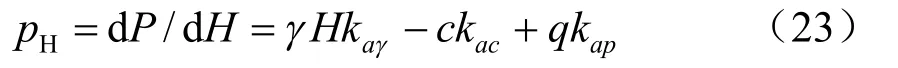
主动土压力的作用点距墙底的高度为
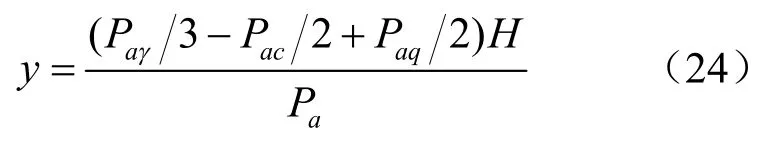
式中:Pa为主动土压力,kaγ,kac,kaq分别为单独考虑重度,黏聚力,超载时的土压力系数。
3 基于混合粒子群算法主动土压力优化计算
基于能量法主动土压力计算可归结为如下优化模型:
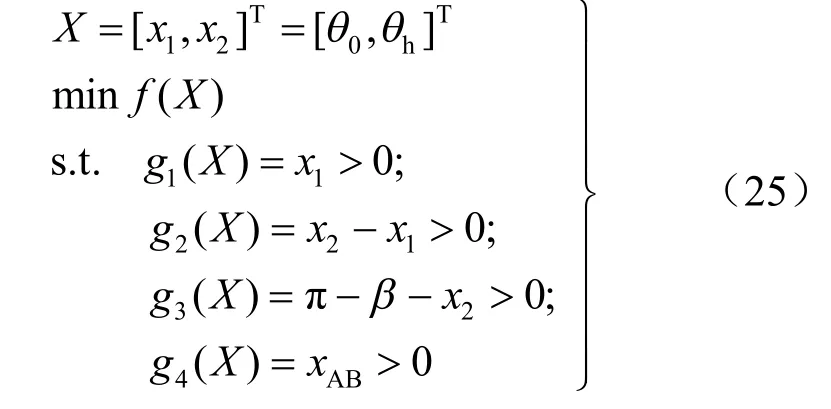
式中:X 为优化设计变量;f (X)为目标函数,计算土压力时f (X)=-Pa,计算土压力系数时f (X)=-kaγ,其中Pa与kaγ分别按式(17)与式(20)计算;gj(X)( j=1, 2, 3,4)为约束条件,其中xAB按式(5)计算。
式(25)是一个含有复杂的目标函数和约束条件的非线性规划问题,本文采用适用性强且具有良好的全局搜索能力的粒子群算法[9](PSO)求解。
在PSO 算法中,每个粒子都具有3 个参数:位置矢量X,代表目标函数中自变量的值;速度矢量V,代表粒子飞翔的力向和距离,用来引导粒子不断朝着更好的解空间改变当前位置;适应度fitness,由被优化的目标函数决定,目标函数值越小,则适应度越好。在每一次迭代中,粒子通过跟踪2 个最优解来更新自己,一是粒子本身所找到的最优解,另一个是整个种群目前所找到的最优解。
混合粒子群算法是将自然选择机制与粒子群算法结合,在每次迭代过程中将整个粒子群按适应值排序,用群体中最好的一半的粒子的速度和位置替换最差的一半的位置和速度,同时保留原来每个个体所记忆的历史最优值。
基于以上原理和模型,主动土压力混合粒子群优化算法计算步骤如下:
(1)设定粒子群数目为40,即i∈[1,40]。对每个粒子的当前位置矢量 Xi=[xi,1,xi,2]和速度矢量Vi= [vi,1,vi,2]在变量范围内[0, π-β ]随机赋予初始值;
(2)根据每个粒子当前的iX 计算其适应度。若gi(X)>0 成立,则fitness(i)=f (iX );否则,将一个远大于正常土压值的大数赋给适应度函数作为此粒子的适应值以使其受到惩罚,例如fitness(i)=10 000;
(3)将各微粒的位置和适应值存储在各微粒的个体最好位置pbest 中,将所有pbest 中适应值最优个体的位置和适应值存储于群体最好位置gbest 中;
(4)按式(26)和(27)更新每个微粒的速度和位置:
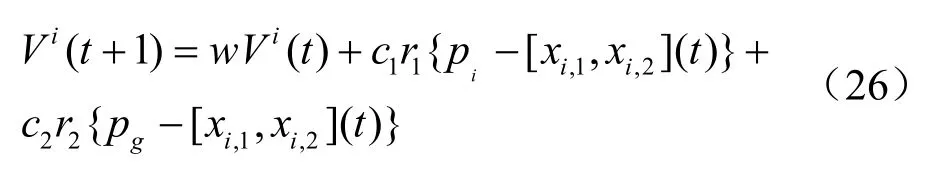

式中:t 为迭代的步数;pi为个体最优适应值对应的[xi,1, xi,2]值,即第i 个粒子最优适应值对应的的[0θ ,hθ ]值;pg为群体最优适应值对应的[0θ ,hθ ]值;w 为惯性权重因子,文中取w=0.5;c1、c2为正的学习因子,文中取c1= c2=2;r1、r2为[0,1]范围内的均匀随机数。
(5)对每个微粒,将其适应值与其经历过的最好适应值比较,如果较好,则将其对应的位置作为当前的最好位置,然后比较当前所有pbest 和gbest的值,更新gbest;
(6)将整个粒子群按适应值排序,用群体中最好的一半的粒子的速度和位置替换掉最差的一半的位置和速度,保持pbest 和gbest 不变。
(7)设定最大迭代次数为100 步,达到迭代次数后则输出结果,即土压力最大时的0θ 、hθ 值以及土压力或者土压力系数的值。
4 结果对比分析
当墙背竖直时,对于无超载的砂性土,将c =0,q=0,β =90°代入式(20),运用上述优化方法计算土压力系数kaγ随填土面倾角α 的变化结果,并与文献[3]中结果进行对比。
由表1 知,在不同的填土面倾角下,本文结果与文献[3]结果几乎一致(差值在2%以内)。说明两者的差别对填土面倾斜角度不敏感。
当填土面水平时(α =0°),土压力系数kaγ随墙背倾角β 的变化与文献[3]结果对比如表2 所示。

表1 墙背竖直时与文献[3]结果对比 Table 1 Comparison between results obtained by reference [3] and with a vertical wall
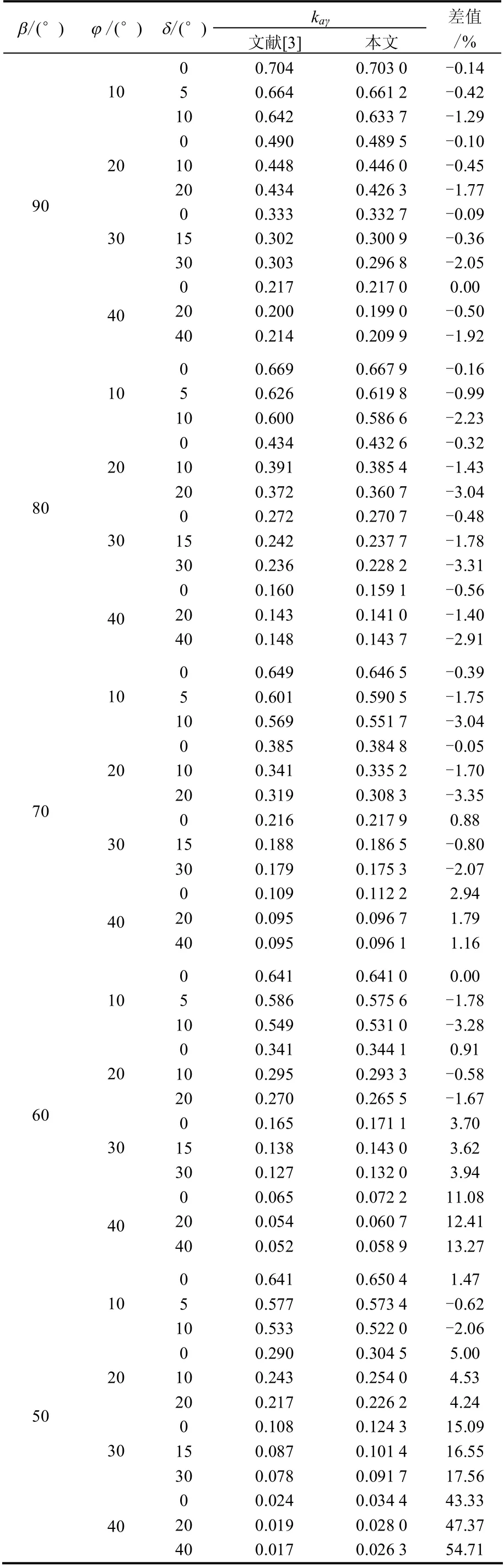
表2 填土面水平时与文献[3]结果对比 Table 2 Comparison between results obtained reference [3] and with horizontal backfills
从表2 中选择部分数据绘成更直观的图5。

图5 填土面水平时差值随墙面倾角的变化(δ =φ /2) Fig.5 Difference varying with wall angle for horizontal backfills(δ =φ /2)
从图可以看出,当墙面与水平面的夹角为90°、80°、70°时,两者差值接近于0。而当墙背向内倾斜角度大于30°时,两者存在明显的差别,尤其是填土摩擦角较大时,本文比文献[3]的计算结果大50%左右。将两者结果与朱大勇等[10]的极限平衡解对比如表3 所示。
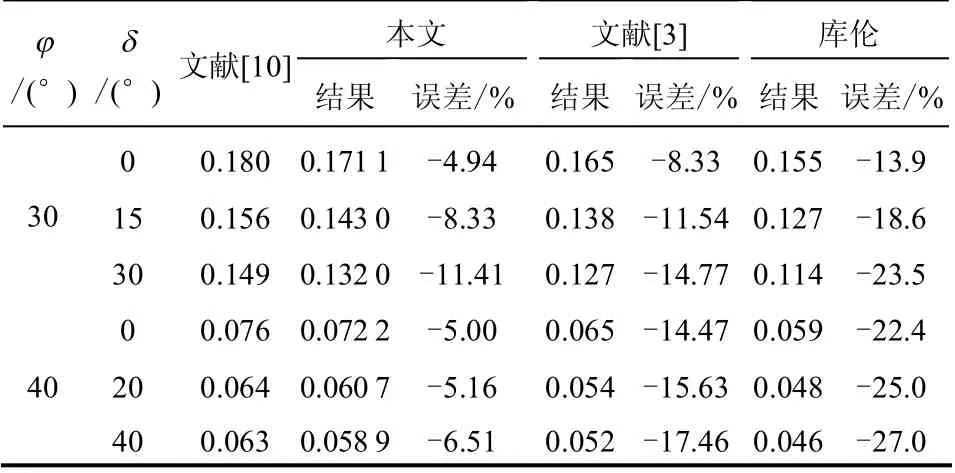
表3 墙背向内倾斜30°时土压力系数对比 Table 3 Comparison of active earth pressure coefficients while the wall angle is 30°
从表3 中可以看出,当墙背倾角较大时,本文比文献[3]更接近文献[10]的计算结果,笔者认为这是由不同的破坏机构导致的。由于文献[3]没有对对数螺线中心进行搜索,所以在一些特定情况下不能搜索到土压力系数的最优值(最大值),从而小于实际值。显然,此时的库伦理论精度更小,因为墙背倾角较大时,真实滑动面与平面滑动面的假定存在较大的差异。
5 实例验证
四川建筑科学研究所在四川简阳做的重力式挡土墙试验[11]:墙背竖直,墙高为4 m,土天然重度γ =19.34 kN/m3,不排水三轴快剪指标φ = 16.63°、δ =8.32°、c=4.7 kPa。
计算结果见表4。同时给出了建筑地基基础规范[12]推荐方法的计算结果与实测结果。

表4 本文计算结果 Table 4 Result of the article

表5 本文计算结果与实测值对比 Table 5 Comparison of results obtained by the article and measured date
显然,本文对黏性土的计算结果比规范推荐方法计算结果更接近实测值。
6 结 论
(1)本文基于能量法和混合离子群优化算法,假定滑动面为对数螺线滑裂面,得到了一种新的主动土压力及其系数计算方法。
(2)对于黏性土,通过与一重力式挡墙试验结果对比分析发现,本文结果与实测值误差仅为5.4%,表明本文方法计算结果可靠。
(3)对于无超载砂性土的土压力系数,本文方法计算结果与经典的极限分析上限解在墙面倾角较小时基本一致,但当墙面倾角较大时,经典解明显偏小,与本文解最大差别达54.71%,而本文解与基于最优性原理的极限平衡解较接近。
[1] TERZAGHI K. Theoretical soil mechanics[M]. New York: [s. n.], 1943.
[2] 赵树德, 赵树惠. 用对数螺线滑动面计算挡土墙主动土压力[J]. 西安建筑科技大学学报, 2002, 34(4): 342-345. ZHAO Shu-de, ZHAO Shu-hui. Calculation of earth pressure of active retaining wall with logarithmic spiral sliding surface[J]. Xi'an Univ. of Arch.& Tech., 2002, 34(4): 342-345.
[3] CHEN W F. Limit analysis and soil plasticity[M]. New York: Elsevier Scientific Publishing Company, 1975.
[4] 范文, 沈珠江, 愈茂宏. 基于统一强度理论的土压力极限上限分析[J]. 岩土工程学报, 2005, 27(10): 1147-1153. FAN Wen, SHENG Zhu-jiang, YU Mao-hong. Upper-bound limit analysis of earth pressure based on unified strength theory[J]. Chinese Journal of Geotechnical Engineering, 2005, 27(10): 1147-1153.
[5] 杨建民. 基于非线性破坏准则的主动土压力上限计 算[J]. 岩土力学, 2009, 30(2): 503-508. YANG Jian-min. Upper bound solution for active earth pressure based on a nonlinear failure criterion[J]. Rock and Soil Mechanics, 2009, 30(2): 503-508.
[6] YANG Xiao-li. Upper bound limit analysis of active earth pressure with different fracture surfaces and nonlinear yield criterion[J]. Theoretical and Applied Fracture Mechanics, 2007, 47(1): 46-56.
[7] SOKOLOSKII V V. Statics of granular media[M]. New York: Pergamon Press, 1965.
[8] 顾慰慈. 挡土墙土压力计算手册[M]. 北京: 中国建材出版社, 2005.
[9] 龚纯, 王正林. 精通Matlab 最优化计算[M]. 北京: 电子工业出版社, 2009.
[10] 朱大勇, 钱七虎. 极限平衡法计算土压力系数的新途径[J]. 土木工程学报, 2002, 33(1): 63-68. ZHU Da-yong, QIAN Qi-hu. New approach for computation of earth pressure coefficients based on limit equilibrium method[J]. China Civil Engineering Journal, 2002, 33(1): 63-68.
[11] 四川省建筑科学研究院. 重力式挡土墙的试验研究[R]. 成都: 四川省建筑科学研究院, 1982.
[12] 中华人民共和国国家标准. 建筑地基基础设计规范[S].北京: 中国建筑工业出版社, 2002.

