高黏性铝土矿放矿流动性试验与微观力学研究
张春阳,曹 平,范 祥,林 杭,万琳辉
(中南大学 资源与安全工程学院,长沙 410083)
1 引 言
颗粒物质的研究已有很长的历史,物理学中正式有关颗粒的研究至少可以追溯到18、19 世纪,但当时涉足这一领域的科学家寥寥无几[1]。有关颗粒物质在筒仓中的研究最早见H.Janssen 提出的粮仓效应[2]。近些年来,国内外学者对颗粒物质在不同颗粒属性、筒仓结构、尺寸等因素下的流动特点及力学关系进行了大量研究[3-10],他们的研究成果在化工、材料、农业以及煤炭行业中都得到了较好的应用。
高黏性铝土矿作为一种散体颗粒物质,其含泥量高、细颗粒多,并含有一定量水,不同于化工、材料、农业、煤炭等行业中的颗粒。高黏性铝土矿堆放时间过长,很容易黏结成块,引发堵塞、卡斗、起拱,严重影响矿山正常生产,给矿仓的维修保养带来诸多不便,人工清理安全系数低。
针对中铝洛阳铝矿放矿这个难题,公司近几十年来先后采取过多种方法,例如空气泡、底部振动放矿机、人工捅矿等,但这些方法都未能从根本上解决问题。人工捅矿需要工人进入矿仓内部,安全性无法得到保障;如果遇到下雨天气,矿石含水量增加,处理起来更加困难。面对这个棘手问题,现有的一些理论和方法已经证明并不适用,因此,研究新的助流技术十分必要。本文结合理论分析、试验、数值模拟,经过多次试验与改进,提出了新的振动助流技术,很好地解决了这个困扰中铝公司几十年的难题,研究成果具有重要的理论与经济意义。
2 矿块移动的极限平衡条件
松散矿石在料仓中流动存在一个应力极限平衡状态,在这种状态下,整个矿石或者它的某一区域内的初始抗剪力和内摩擦力刚好被克服,这种应力极限状态的出现引起矿石在料仓内的运动[11]。设想通过松散矿石某一点有一具有法线n 的任意微面。在该微面上作用着法向应力分量 σn和切向应力分量τn,如图1 所示,其中σc为换算黏性应力,φ 为内摩擦角,保证松散矿岩不发生滑动的不等式将有≤(σn+σc)tan φ,且 σn≥ -σc。为了达到松散矿岩的应力平衡,在通过该点的任意微面上应当满足该不等式。
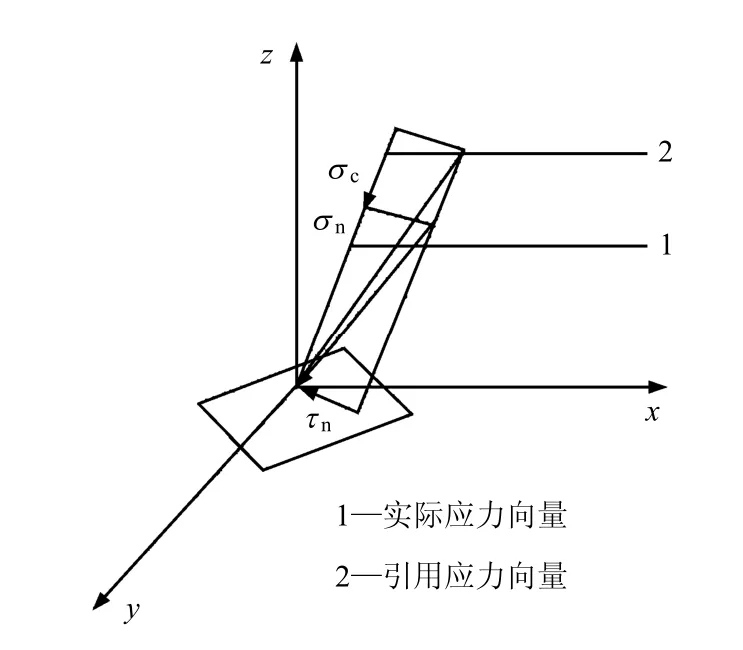
图1 某点应力示意图 Fig.1 Stress sketch of a point

当式(1)成立时,就是松散矿岩的应力极限平衡状态,这也是松散矿岩极限平衡条件的力学特性。对于松散矿岩的应力极限平衡条件也可做如下理解,即在极限状态时,切向应力的绝对值与作用在同一微面上法向应力的线性函数间的最大差值等于0。在松散矿岩发生剪切移动的瞬间,则式(1)就会成立,这就是滑动面的极限平衡条件。
3 室内相似试验
3.1 相似条件
相似模拟试验必须满足模型与实物几何相似和主要物理量相似。影响放矿过程的因素有几何尺寸l、松散体承受的压力F、正应力σ 、剪应力τ 、黏聚力c、内摩擦角φ、外摩擦角wφ 、散体的密度ρ、质量m、颗粒运动速度v、加速度a、位移s 和时间t。以Cl、CF、Cσ、Cτ、cC 、Cφ、wCφ、Cp、Cm、Cv、Ca、Cs、Ct表示对应各量的相似常数,可以推导出相似指标[12]:
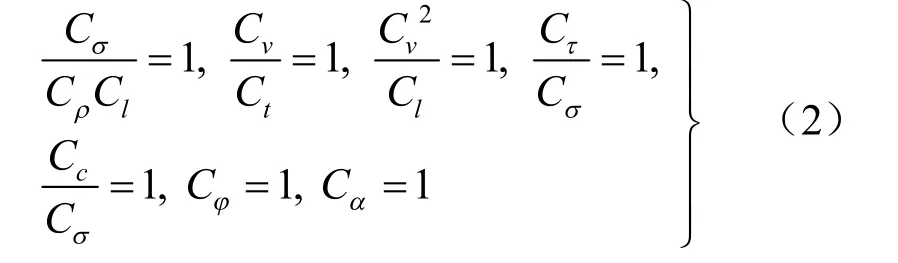
在本试验中采取几何相似比为1/12,即Cl=12,所以试验要满足:
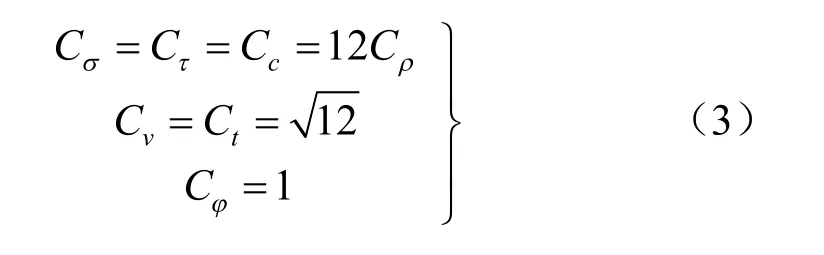
上述相似关系式在模拟放矿试验中一般是很难完全满足的。但试验证明,只要尽量做到尺寸相似、内摩擦角相似、边界条件、初始条件等相似,模拟试验可用于问题的研究[12]。
3.2 相似模型试验
通过试验模拟在不同的含水率、漏斗壁摩擦系数、有无助流栅格3 种情况下矿石的流动情况,试验过程如下:
(1)不同含水率试验
通过烘干检测3 种样品的含水率,结果分别为8.2%、9.5%、10.8%。含水率对矿石流动性影响如图2 所示,由试验结果可知:
① 当含水率为8.2%时,矿石自身能够实现稀疏的整体流动,并顺利放出。
② 当含水率为9.5%时,在放出过程中会发生堵塞,需要借助外力破拱才能继续流动,前后施加了5 次外力破拱,在放出过程中会出现鼠洞。
③ 当含水率为10.8%时,矿石流动更加困难,至少需要7 次外力破拱,在每次停止流动的过程中,也伴随着鼠洞的出现,边角粘结少量矿石未能放出。

图2 含水量影响 Fig.2 Influence of water content
(2)不同仓壁摩擦系数试验
试验选取含水率为8.2%的矿石样品,通过在模型漏斗处粘贴不同摩擦系数的砂纸来改变仓壁摩擦系数,试验分为无砂纸、细砂纸、粗砂纸3 种情况,试验观察如图3 所示。可以看出,随着仓壁摩擦系数增大,矿石流动性受到很大抑制。

图3 不同摩擦系数影响 Fig.3 Influences of different friction coefficients
(3)改流体试验 矿石在矿仓流动时,中间部分的流动性最好,而周边流动性最差,因此,考虑在模型顶部安装助流格栅来提高周边矿石的流动性,安装效果及试验过程如图4 所示。可以看出,助流格栅并没有起到很好的助流效果,反而更容易发生堵塞。

图4 助流格栅影响 Fig.4 Influence of flow-aiding grid
3.3 试验结果分析
(1)含水率对矿石流动性的影响很显著,含水率从8.2%到10.8%,矿石流动性急剧下降,由于含水率的增加,使得矿粒间以及矿粒与仓壁间的黏聚力c 增长很快,c 的增加很容易使矿石粘结成块,影响矿石的流动性。虽然含水率会减少矿石间的内摩擦系数f,但摩擦力的减少量相比c 来说偏小。如果含水率继续增加,根据吴爱祥等[13]的研究,当含水率达到饱和时特别容易发生跑矿事故。
(2)仓壁摩擦系数对矿石流动性影响也很大,采用低摩擦系数的漏斗壁内衬材料可以减小漏斗壁的外摩擦系数f,降低漏斗壁与矿石的摩擦力,从而减少结拱几率。
(3)助流格栅在含水率较低的情况下(8.2%)可以起到优化矿石流动方式和提高矿石流动性的作用,但在含水率较高的情况下(10.8%),助流栅格一般不能达到助流目的,相反还会增加堵矿的可能性,因此,助流格栅不适合在洛阳铝矿矿仓内使用。
4 相似试验离散元数值模拟
PFC2D二维颗粒流程序,是通过离散单元法模拟圆形颗粒介质的运动及其相互作用。PFC 是著名学者Peter Cundall 主持下采用细观离散元理论开发的一种商业数值软件[14],可以广泛地应用于研究细观结构控制问题。以牛顿第二定律和力-位移定律为基础,模拟颗粒间的接触、运动和相互作用关系。
4.1 模型建立
模型分为2 部分,通过编制颗粒单元的生成文件实现。第1 部分是墙体,用wall 命令创建仓筒、和漏斗;第2 部分是颗粒,用ball 命令来生成颗粒。模型还在墙体上定义了虚拟传感器,可以随时记录墙体接触压力的变化情况,如图5 所示,图中4、5、6、7 号虚拟传感器安装在漏斗部分,8、9、10、11号虚拟传感器安装在墙体部分。
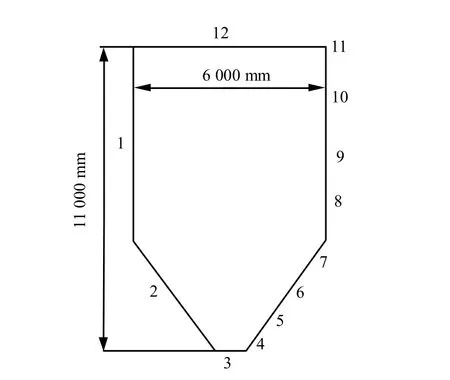
图5 料仓模型 Fig.5 Hopper model
本模型中颗粒直径分布为0.05~0.15 m,颗粒数量5 000~5 500个。墙与颗粒的刚度值结合PFC2D自身特点,保持一致;颗粒-颗粒及颗粒-墙之间的摩擦系数分别定义为内摩擦系数与外摩擦系数,为了更直观地展现模拟结果的差异,并参考相关基本力学试验数据,选取相关的摩擦系数及黏聚力。基本物理力学参数如表1 所示。
4.2 各种影响因素下颗粒流动性分析
(1)含水率对流动性影响
通过改变黏聚力和摩擦系数来模拟不同含水率对颗粒流动性的影响。模拟分为不含水、含水和含水过多3 种情况。结果表明在没有水的情况下矿石能够顺利流出;当含水率增加到一定程度,矿石就很难流出,容易发生堵塞事故,放出的模型小颗粒相互粘结;当含水率达到饱和后,如果继续加水,那么矿石流动性会变得更好,如图6 所示。

表1 颗粒流模拟基本参数 Table 1 Basic parameters for particle flow simulation

图6 含水率影响(550×104 步) Fig.6 Influence of water content
含水率之所以引起矿石颗粒流动性变化是由于:
①含水率影响外摩擦系数,随着含水率的提高,外摩擦系数相应增大,当含水率增加到某一限度时,外摩擦系数出现最大值,随后外摩擦系数随水份增加呈下降趋势,这是因为增加的水份开始易被颗粒吸收,增加了颗粒与壁之间的吸附力,所吸收的水份越多,则吸附力越大,直至达到最大值,即对应于最大的外摩擦系数。当颗粒含水率增加至某一限度后,就不再被颗粒吸收,多余水份以自由水的形式存在,在颗粒和仓壁之间起润滑作用,使颗粒容易沿仓壁滑动,因而外摩擦系数反而降低。
②含水率影响内摩擦系数。含水率为0 时,颗粒之间摩擦表现为干摩擦,稍增加含水率后,颗粒表面形成一层水膜,在散体颗粒之间起到润滑作用,引起内摩擦力的降低,再增大含水率,则水份润滑作用引起的内摩擦力降低趋于极值。
③含水率影响黏聚力,随着含水率的增加,颗粒间形成水膜,在气水界面上产生表面张力同时,存在于颗粒之间的胶凝物质和水份生成的水化结晶物产生黏聚作用。因此,黏聚力逐渐增加,表现出极值的存在,当颗粒中所含水份达到饱和状态之后,破坏了颗粒间形成的水膜和表面张力,因而黏聚力又有所降低。所以有时在处理溜井堵塞事故时,采用向溜井中大量灌水的办法,其原因就在于此[15]。 (3)仓壁摩擦系数影响
图7 是仓壁摩擦系数为0.1 和1.0 时的放出情况,两个模型的运算步数都相同。摩擦系数为0.1时,颗粒流动形态主要为整体流,如图7(a)所示。当摩擦系数为1.0 时,颗粒流动速度缓慢,且不均匀,如图7(b)所示。由于仓壁处摩擦系数大,阻碍了颗粒的流动,有成为中心流(管状流)的趋势。

图7 仓壁摩擦系数影响(550×104 步) Fig.7 Influence of wall friction coefficient
(4)改流体影响
相似试验中采用安装助流格筛的办法,不但保护了仓底结构,同时也抑制了仓内中间矿石下落速度,改善了周边矿石流动性,在一定程度上起到了助流作用。由模拟结果可以看出(图8 所示),装了改流体以后,颗粒流动速度变化不是很大,但改变了颗粒流动形态,仓体中间颗粒流动性受到一定抑制,使得颗粒流动相对比较均匀。

图8 改流体影响(550×104 步) Fig.8 Influence of flow change device
4.3 各影响因素下仓壁接触压力分析
影响因素的变化会改变仓壁接触压力分布,颗粒含水率对仓底部接触压力影响很大,如图9 所示。图10 显示在其他条件相同时,摩擦系数越大,仓体漏斗部分接触压力越小,反之越大。
图11 表明,改流体不但可以改变流动形式,同时也可以改变仓壁接触压力的分布。在没有改流体的模型中,仓内各部分接触压力变化较大,且不均匀,容易造成局部受力过大而破坏仓体。加了改流体后,仓壁的接触压力分布更为合理,大幅减少了漏斗处的压力。
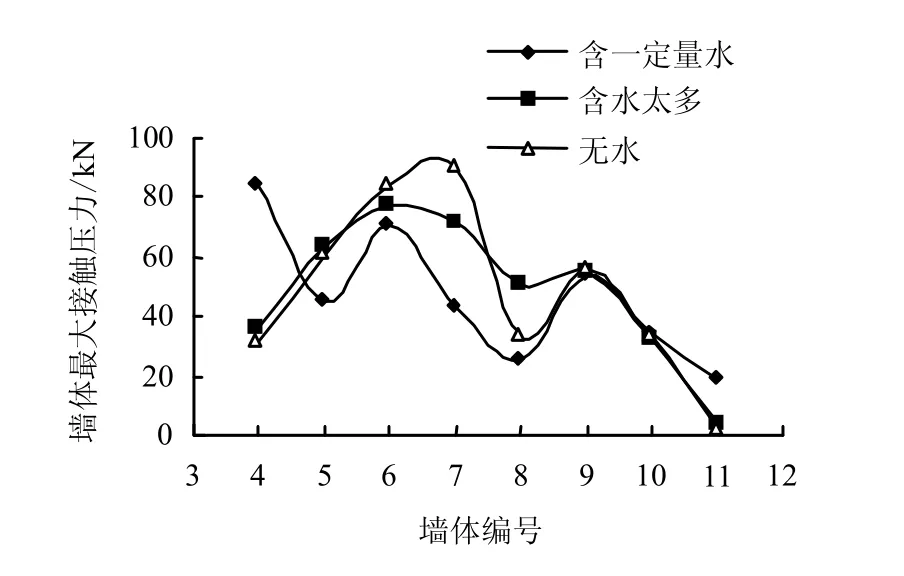
图9 含水率影响 Fig.9 Influence of water content
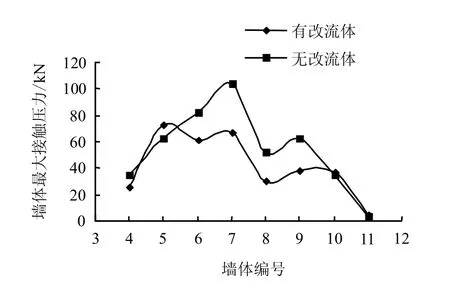
图11 改流体影响 Fig.11 Influences of flow change device
4.4 颗粒流动机制研究
图12 为颗粒流动时仓壁压力动态监测曲线,曲线显示,颗粒在流动过程中仓壁接触压力呈波浪状起伏,表明仓壁压力随颗粒间动态压力拱的结拱和破拱处于波动之中,也表明在颗粒流动过程中,结拱-破拱过程交替出现。
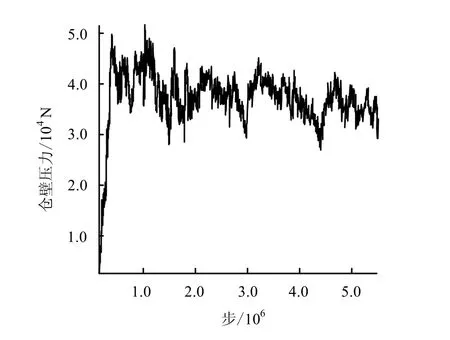
图12 仓壁压力波动情况 Fig.12 Wall force fluctuation
如果由于其他原因导致颗粒堵塞漏斗口后,监测显示,仓壁压力不再波动,如图13 所示。以上结果也隐含了颗粒放出时的流动规律与力学机制。
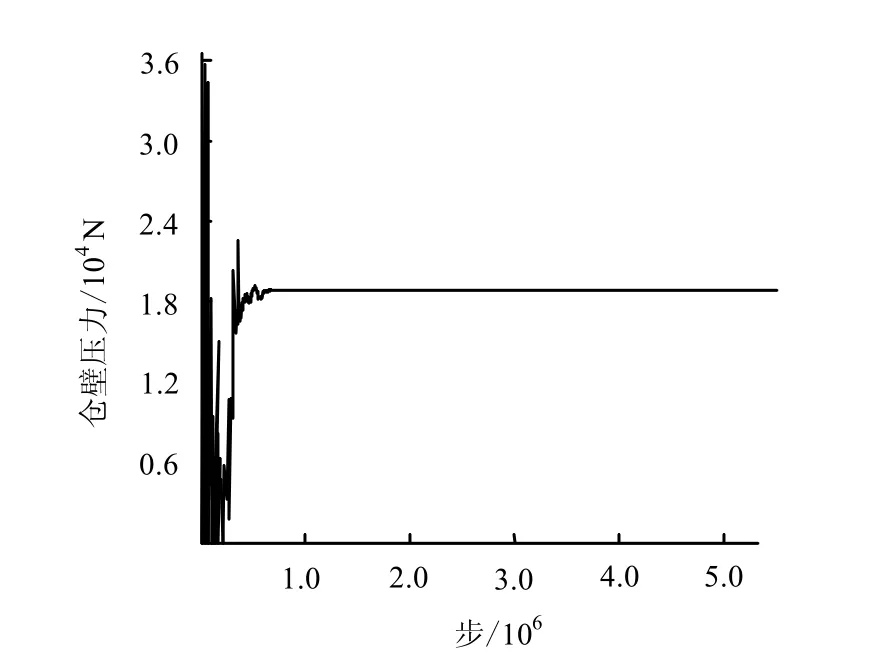
图13 仓壁压力趋于恒定 Fig.13 Wall force remains constant
5 矿石颗粒流动性助流研究
5.1 现场试验
考虑到中铝洛阳铝矿矿仓特有结构,结合颗粒流动机制研究结果,设计了一种全新的仓内垂悬式振动器,使它的振动棒插入到料仓截面突然收缩部位进行振动,以达到改善矿石流动性的目的;在矿仓漏斗部分安装超高分子量聚乙烯板材,减小仓内摩擦系数,从而改善仓底部的流动性。
现场工业试验时先进行重力放矿,等重力放矿停止后再开启振动器,发现矿石又开始流动。这样循环结合重力放矿和振动放矿,矿石最终都顺利地放完,同时也节省了耗电量。
本方案特别在含水率较高、矿石容易堵塞的情况下效果非常明显,放出率达到100%,安全系数达到95%以上[16],如图14 所示。
5.2 振动助流微观力学研究
用PFC2D自带的fish 语言编辑振动模型,振动器安装在矿石最容易黏仓的死角部位,材料参数和料仓尺寸保持不变,振动频率为70 Hz,振幅为 1.2 mm,振动器安装位置为(0.8,4.0)、(5.2,4.0)。颗粒流模拟结果如图15 所示。

图14 振动助流装置及效果 Fig.14 Vibration flow-aiding devices and its effect
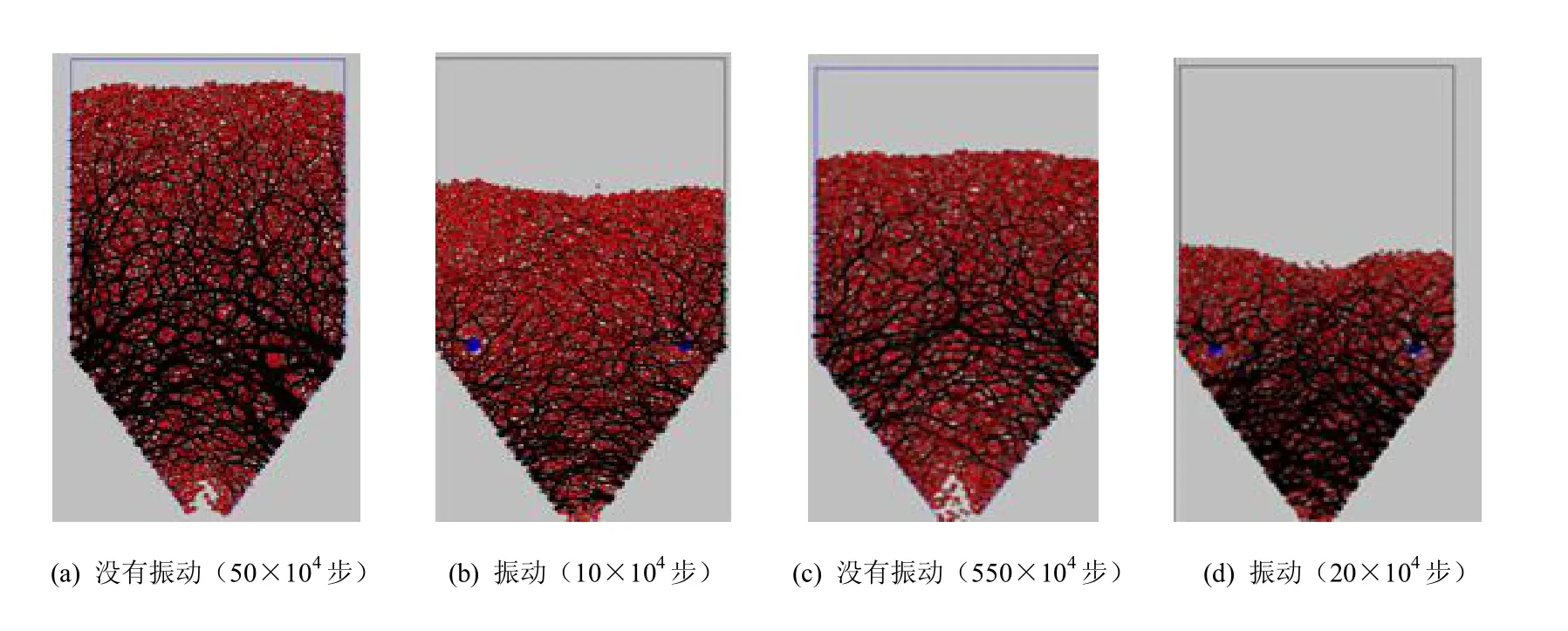
图15 振动放矿效果对比图 Fig.15 Comparison of vibration discharge effect
由图可知,在加入振动器后,颗粒的流动性大为改善,只需要运算20×104步,仓筒部分的矿石就差不多放完,并且中心处矿石流动更快,仓壁两边的颗粒迅速向中心运动。侧压力分布如图16 所示,可见在振动助流条件下,颗粒对仓壁的侧压力大为减小。
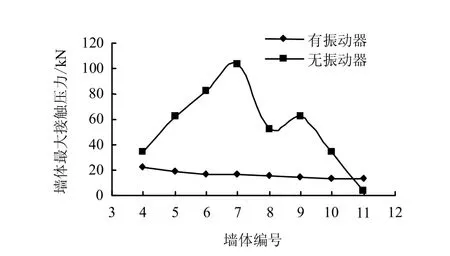
图16 仓壁压力极限值对比 Fig.16 Comparison of hopper wall max force
6 结 论
(1)以相似理论和放矿理论为基础,设计模型进行底部放矿物理模拟试验,再现了现场放矿全过程,确定了影响洛阳铝矿高黏性铝土矿流动性的主要因素。
(2)运用离散元软件PFC2D进行数值模拟,加深入对矿石流动性影响因素的认识。数值模拟揭示了放矿过程中仓壁压力的动态变化,为高黏性铝土矿助流研究提供了重要依据,仓壁侧压力动态变化也隐含了颗粒流动的力学机制。
(3)设计的仓内悬垂式振动助流器结合仓壁超高分子量聚乙烯板材很好地改善了矿石流动性,放出率达到100%,安全系数达到95%以上。数值模拟不但验证了该助流方法的优越性,而且也极大地降低了仓壁压力。
(4)研究结果有助于在矿仓设计、建造,降低仓体维修频率,延长矿仓使用寿命,提高放矿效率和生产安全系数等方面的进一步深入研究。新设计的助流方案具有重要的参考与推广价值,为处理类似的仓体问题提供重要借鉴。
[1] 陈唯. 电场作用下颗粒流动的行为研究[D]. 北京: 中国科学院物理研究所, 2001.
[2] 张国琴, 鲍德松, 张训生. 颗粒物质运动规律的研究[J]. 科技通报, 2004, 20(5): 381-384. ZHANG Guo-qin, BAO De-song, ZHANG Xun-sheng. Studying the dynamic of granular matter[J]. Bulletin of Science and Technology, 2004, 20(5): 381-384.
[3] CLEARYPAUL W, SAWLEY MARK L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge[J]. Applied Mathematical Modelling, 2002, 26(2): 89-111.
[4] BEENA S, ASHMAWY A K. Influence of inherent particle characteristics on hopper flow rate[J]. Powder Technology, 2003, 138(1): 46-50.
[5] ANSHU A, CURTIS J S. Segregation of cohesive granular materials during discharge from a rectangular hopper[J]. Granular Matter, 2010, 12: 193-200.
[6] ANSHU A. Predicting discharge dynamics from a rectangular hopper using the discrete element method (DEM)[J]. Chemical Engineering Science, 2008, 63(24): 5821-5830.
[7] 周健, 张昭, 杜明芳. 漏斗形状改变对筒仓压力影响的细观研究[J]. 特种结构, 2006, 23(4): 14-16. ZHOU Jian, ZHANG Zhao, DU Ming-fang. Research in detail for influence of pressure in silo after changing the funnel form[J]. Special Structures, 2006, 23(4): 14-16.
[8] 杜明芳, 张昭, 周健. 筒仓压力及其流态的颗粒流数值模拟[J]. 特种结构, 2004, 21(4): 39-41. DU Ming-fang, ZHANG Zhao, ZHOU Jian. Pressure of silo and imitation of grain digit fluidity[J]. Special Structures, 2004, 21(4): 39-41.
[9] 李海旺, 刘静, 树学峰. 裤型漏斗型钢贮煤仓散料压力分布研究[J]. 工程力学, 2010, 27 (6): 140-146. LI Hai-wang, LIU Jing, SHU Xue-feng. Research on the distribution of granular coal pressure on the wall of a special silo with trouser-shape funnel[J]. Engineering Mechanics, 2010, 27(6): 140-146.
[10] 翟振威, 原国平, 张峰涛. 筒仓贮料流态的颗粒流数值模拟[J]. 山西建筑, 2008, 35(34): 90-92. ZHAI Zhen-wei, YUAN Guo-ping, ZHANG Feng-tao. The PFC DEM simulation of the flow state of silo[J]. Shanxi Architecture, 2008, 35(34): 90-92.
[11] 王昌汉. 放矿学[M]. 北京: 冶金工业出版社, 1982.
[12] 徐挺. 相似方法及其应用[M]. 北京: 机械工业出版社, 1995.
[13] 吴爱祥, 古德生, 戴兴国. 含水量对散体流动性的影 响[J]. 中南矿冶学院学报, 1994, 25(4): 455-459. WU Ai-xiang, GU De-sheng, DAI Xing-guo. The influence of water content on the flow property of bulk solid[J]. Journal of Central South Institute of Mining Metallurgy, 1994, 25(4): 455-459.
[14] Itasca Consulting Group Inc. Particle flow code users' guide[R]. Sudbury: Itasca Consulting Group Inc, 2002.
[15] 吴爱祥, 孙业志, 刘湘平. 散体动力学理论及其应用[M]. 北京: 冶金工业出版社, 2002.
[16] 张春阳. 散体矿岩移动规律模拟及高黏矿岩助流研 究[D]. 长沙: 中南大学, 2009.

