商品住宅价格上涨的空间自回归模型及其实证
兰 峰,张 媛
(西安建筑科技大学 管理学院,西安 710055)
近年来,我国房地产业迅速发展,住宅价格逐年攀升,各种房地产政策及保障制度出台后,却不能很好的控制的这种局面。本文试图从空间计量经济学角度出发,论证城市之间商品住宅价格存在的空间依赖性。且建立合理的空间自回归模型进行参数估计和检验,分析了商品住宅价格上涨的主要因素,并进一步探讨了城市之间商品住宅价格影响的方向。本文的研究结论能为商品住宅价格的形成机理奠定了理论基础,同时为政府宏观调控提供一个视角,作为政府政策的参考。
1 变量的选择
本文选取商品住宅的平均销售价格作为因变量。对于自变量的选取,主要基于均衡价格理论,在大量研究商品住宅价格影响因素结论的基础上,本着可比性、相关性、可量化以及数据可获得性四大原则总结出主要影响因素。供给方面的因素包括土地成本;需求方面的因素包括地区生产总值、城镇可支配收入、城市人口总数以及人均居住面积[1]。在此基础上,本文汲取空间计量经济学的思想,认为空间地理因素也是影响商品住宅价格上涨的因素。
2 商品住宅价格上涨的空间自回归模型的构建
商品住宅价格最终由需求和供给决定的,是住宅市场供需平衡后的结果[2]。这种研究方法是建立一个商品住宅市场的供需均衡价格模型,在开发企业与消费者获得使用住宅的最大化效用中得出模型的参数[3],最后通过供需平衡推导出商品住宅价格。
住宅市场需求函数模型为:

住宅市场供给函数模型为:

其中,HQd为商品住宅需求量;Ph为商品住宅价格;X为其它需求变量;β0,β1,β2为变量系数;HQs为商品住宅供给量;∂为系数。
根据供需价格均衡理论,最终整理为如下关系式:

式(3)是商品住宅均衡价格的函数形式,利用这个模型就可以得到多种因素对住宅价格的影响,以均衡价格P为因变量,C为住宅成本,X为影响商品住宅价格变动的其他因素。
本文在研究商品住宅价格上涨时,运用空间计量经济模型论证其是否能更好的解释城市住宅价格的变动。在空间计量经济模型中,关于空间依赖性主要包括两种模型,空间滞后模型和空间误差模型[4]。
空间滞后模型(SAR)表达式为:

其中,ρ是空间自回归系数,W表示空间权重矩阵,X是解释变量数量矩阵,β为自变量的系数,ε是随机扰动项。
空间误差模型(SEM)表达式为:

其中W表示扰动项的空间自回归权重矩阵,λ是扰动项ε的空间自回归系数,且u服从正态分布。
结合以上分析影响商品住宅价格上涨的主要因素,建立均衡价格的空间计量经济模型,如下:
均衡价格的空间滞后模型,方程(4)可以表示为:

均衡价格的空间误差模型,由方程(5)式得:
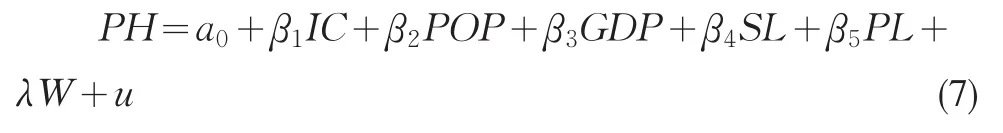
3 实证研究
3.1 样本、变量的选取以及数据来源
3.1.1 样本选取
本文选取的是1998~2009年(因统计数据滞后一年,数据选取至2009年)以北京为中心的共8个城市所组成的面板数据,共计12×8=98组。8个城市分别为:北京、天津、石家庄、太原、呼和浩特、济南、沈阳、长春。选择8城市的理由如下:鉴于本文研究主要目的是检验各城市之间的商品住宅价格是否存在空间依赖性,并通过空间计量经济模型对商品住宅价格的主要影响因素进行分析,首先选取商品住宅价格上涨的典型城市北京为代表,而后选取其周边相对连续的共8个大中城市。
3.1.2 变量选择及数据来源
①商品住宅价格(PH)。用住宅平均销售价格表示,单位:元/平方米;
②居民可支配收入(IC)。用各市城镇居民人均可支配收入表示,单位:元;
③城市人口(POP)。用城市年末人口总数表示,单位:万人;
④地区生产总值(GDP)。用各城市地区生产总值实数表示,单位:亿元;
⑤居住面积(SL)。用各城市人均居住面积表示,单位:平方米;
⑥土地价格(PL)。用各城市土地交易价格指数表示,并将原环比指数处理为以1998年数据为基数的数据。以上变量的统计数据主要来源于各城市的统计年鉴、各城市的统计公报以及中国房地产统计年鉴,部分数据来源于中国统计年鉴和中国城市统计年鉴。
3.2 空间权重矩阵的建立
对于空间权重矩阵的设定,一般通过两种信息进行设定,一是通过经纬度坐标设定;二是通过区域的相对位置设定。目前采用相对位置信息量化建立二进制空间邻接矩阵的方法较多也较容易,但是本文中研究的截面对象是城市,区域不连续,运用经纬度坐标生成的权重矩阵相对准确。建立的空间权重矩阵如下:

3.3 空间相关性检验
研究整个区域对象上的城市之间商品住宅价格是否存在空间相关性,一般采用全局空间自相关指数Moran’s I,通过指标的数值所在的范围,判断不同的城市之间的住宅价格在空间上是否存在一定的规律性。运行结果如表1。

表1 商品住宅价格的Moran’s I指数
从上表的数据结果可以明显看出,1998~2009年8个城市之间的商品住宅价格存在明显的正相关性,空间相关系数为0.2796,拒绝无空间相关性假设的概率为0.000,这说明各城市之间的商品住宅价格存在着显著的空间相关性。
3.4 自回归模型的选择
本文主要通过LM-Lag和LM-Error的指标值判断:
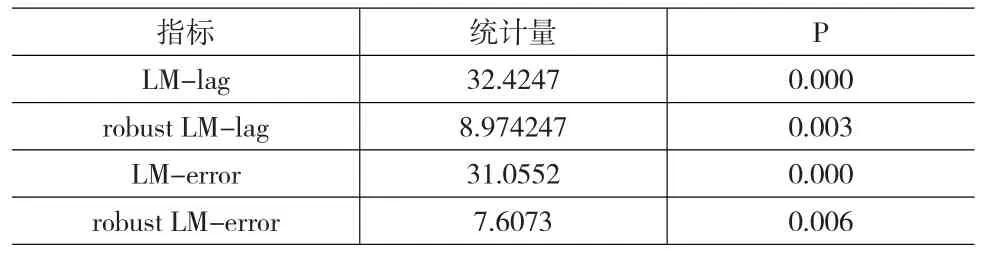
表2 LM检验结果
从LM检验检验结果可以看出,robust LM-lag的p值小于对应的p值,因此,选择空间滞后模型作为估计模型较合适。
3.5 空间滞后模型的参数估计
为了达到较好的回归效果,采用逐步回归法作为变量进入的方法。以商品住宅价格为被解释变量,城镇可支配收入、人口总数、人均居住面积以及土地价格为解释变量,运用最大似然估计法进行参数估计,得到如表3的结果。
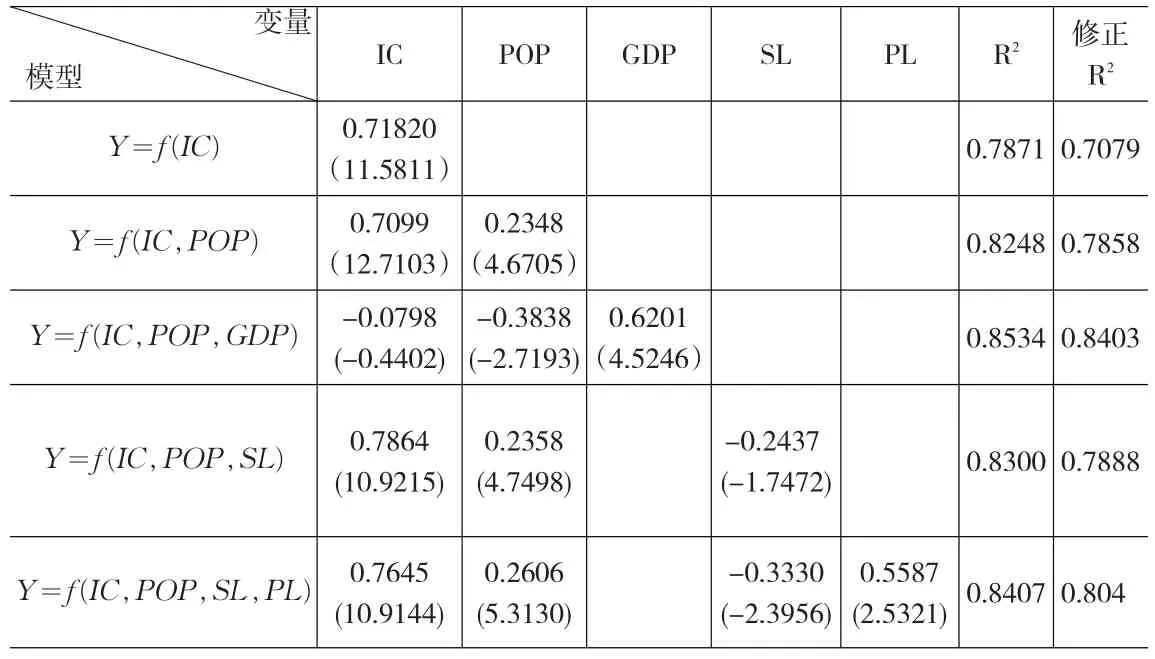
表3 空间滞后模型的逐步回归分析过程及结果
从表3回归的结果可以看出,当引入GDP变量后,从结果看拟合优度值较高,但它的进入引起了原本显著的IC和POP也变为不显著,且回归系数的符号也从正变为负;同样的方法引入其它两变量,SL拟合优度较PL提高,且t检验也是显著的,选SL进入,最后引入PL变量,得到的拟合优度R2和修正后的R2都有所提高,并且各解释变量的t检验都非常显著,最终确定的关于商品住宅价格波动的影响因素的回归函数为:
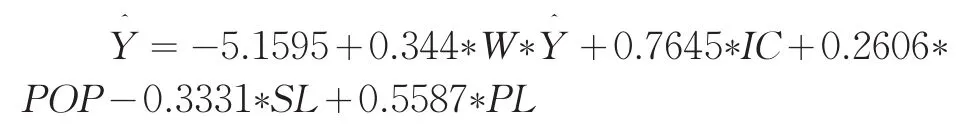
具体模型的估计详细结果图略。
从结果来看,城市年末人口总数(POP)、城镇可支配收入(IC)的影响最为显著,其次,人均居住面积(SL)和土地价格(PL)虽然也通过了置信水平0.05的检验,较其它两个变量显著性水平低,但是从回归系数来看,土地价格的回归系数却达到0.56,仅次于城镇可支配收入对商品住宅价格上涨的影响。
3.6 格兰杰因果检验
在研究商品住宅上涨的影响因素主要有两方面原因:一方面来自于城市内部的自身因素决定的,城镇人均可支配收入、城市人口总数、土地价格以及人均居住面积;另一方面来自于与它相邻或相近的住宅价格上涨的影响。那么,既然城市之间的住宅价格存在空间的相关性,它们之间的商品住宅价格影响方向如何?本文将采用格兰杰(Granger)因果检验的方法进行验证。
3.6.1 单整检验
在进行Granger因果检验之前,需对数据进行单位根检验,检验其序列是否具有平稳性。
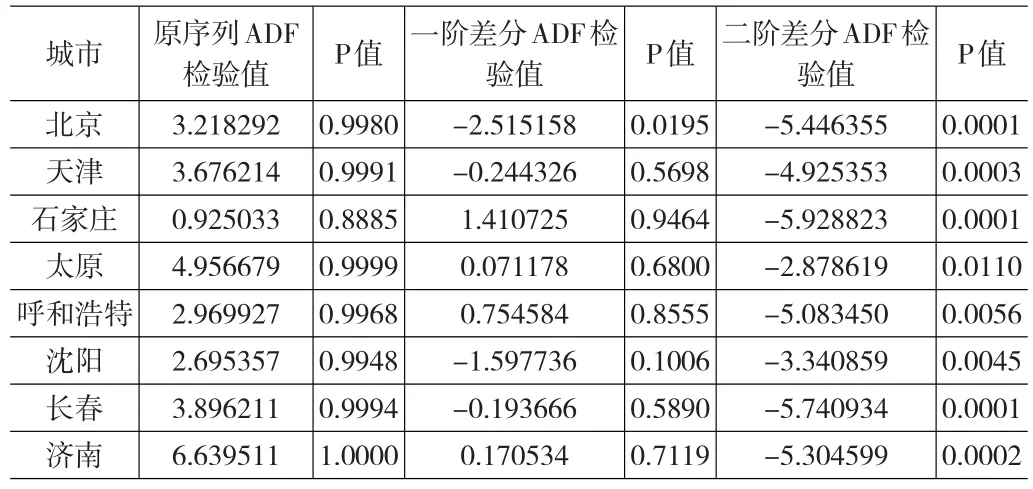
表4 各城市商品住宅价格单整检验结果

表5 北京与其它7个城市的商品住宅价格的Granger因果检验结果
从4表检验结果看出,各城市商品住宅价格均为二阶单整,表明这几个城市的商品住宅价格存在协整关系,其序列较平稳,可以进一步做Granger因果检验。
3.6.2 格兰杰因果检验
下面将主要验证北京与其它几个城市之间的商品住宅价格上涨的影响情况。
从表5Granger因果检验结果来看,北京与太原、呼和浩特之间不存在任何方向的Granger因果关系,这意味着北京的商品住宅价格变动不能显著地引起这两城市的住宅价格的变化。从表中看出,北京与天津、石家庄、沈阳、长春、济南存在的单向的Granger因果关系。
4 模型计量结果解释与分析
(1)空间相关系数的解释。本文采用Moran’s I验证以北京为中心的8个城市商品住宅价格存在显著的空间依赖性。
(2)模型估计结果的解释。通过建立空间滞后模型并进行检验得出:空间地理因素、城镇居民人均可支配收入、城市人口总数、人均居住面积以及土地价格是影响商品住宅价格上涨的主要因素。
(3)Granger因果检验检验结果。检验结果表明:北京与太原、呼和浩特之间不存在Granger因果关系;北京与天津、石家庄、沈阳、长春、济南存在的单向的Granger因果关系。这在一定程度上解释了为什么北京市的商品住宅价格在这个城市圈里处于领军的地位,并说明北京市是这个城市圈住宅价格上涨的源头城市。
因此,城市的住宅价格除了受到自身因素影响外,还会受到来自其它地区的住宅价格变动的传导作用。在实证研究中发现,北京的房价对周边城市的房价具有传导作用。调整像北京这样一线城市的商品住宅价格,对稳定其周边城市的商品住宅价格有着重要的意义。
[1]邓长荣,马永开.我国住宅价格多层面因素模型及其实证研究[J].系统工程理论与实践,2010,(1).
[2]Geoff Kenny.Modeling the Demand and Supply Side of the Housing Market:Evidence from Ireland[J].Economic Modelling,1999,(16).
[3]Meen,GP.The Measurement of Rationing and the Treatment of Struc⁃tural Change in The UK Mortgage Market[J].J.Appl.Econ.,1990,(5).
[4]Anselin L.Spatial Regression.Spatial Analysis Laboratory,Depart⁃ment of Geography and National Centre for Supercomputing Applica⁃tions,University of Illinois,Urbana-Champain,Urbana,IL 61810[Z].2006.

