基于混沌神经网络算法的CPI预测

王 维，范彦伟

（齐齐哈尔大学 经济与管理学院，黑龙江齐齐哈尔161006）

0 引言

居民消费价格指数(CPI)是根据与居民生活密切相关的商品和劳务价格统计出来的物价变动指标。其统计内容包含居民日常消费的全部商品和服务项目，这些商品和服务的价格变动均会影响CPI指数，而它们的价格受市场经济下诸多不确定因素的影响，从而导致CPI表现出较强的非线性特征。将CPI控制在合理的范围内有利于国民经济健康发展，较低的CPI不利于经济增长，而较高的CPI容易引发通货膨胀，引起一系列社会问题。因此，CPI的准确预测关系到国家货币政策走向和企业战略决策。

混沌理论作为非线性动力学的重要发展，已成为一门具有独立理论体系和方法的新学科。其中混沌时间序列预测已被应用到很多领域，即通过某一单变量的时间序列来研究非线性系统整体的混沌行为[1]。其基本步骤是，利用相空间重构方法，将处于混沌状态的时间序列映射到有限维状态空间中，得到混沌吸引子，通过混沌吸引子的总体稳定性、吸引性和内部分形性，实现经济混沌的短期预测。现有文献中，CPI的预测主要有长期预测和短期预测。长期预测模型主要有协整回归预测模型、季节性ARIMA预测模型以及自回归分布滞后预测模型三种[2]。短期预测方法主要运用神经网络预测模型，包括BP网络和RBF网络两种[3,4]。短期预测精度高，但由于输入数据不易收集，只能做当月或下月的CPI预测。长期预测尽管预测时间长，但精度较差。将神经网络与混沌时间序列理论结合进行CPI预测在一定程度上能够弥补上述不足。

1 相空间重构

相空间重构是混沌时间序列分析的基础，根据Takens等人提出的延迟坐标法[5]，对时间序列x={xi|i=1,2,…,N}进行相空间重构

其中m为嵌入维数，τ为时滞，M=N-(m-1)τ为相空间的点数，Xi为m维相空间的相点。

在重构相空间中,延迟时间和嵌入维数的选取十分关键。本文采用C-C方法确定嵌入维m和时滞τ。该方法的基本思想是，先在一定范围内选取多个嵌入维m的值，然后计算出最佳的τ和τw的值，由τ和τw的值最终得到m的值。其具体步骤如下：

对于混沌时序x={xi|i=1,2,…,N}，以嵌入维m，时滞τ，对其进行重构相空间，重构后的相空间为X={Xi}，则嵌入时间序列的关联积分

其中m为嵌入维，N是时间序列的数据个数，r为计算中所取的搜索半径，τ为时滞，M=N-(m-1)τ表示m维相空间中嵌入点数目，θ为Heaviside函数；θ(x)=0,若x＜0；θ(x)=1,若。

关联积分是个累积分布函数，表示相空间中任意两点之间距离小于r的概率。这里点与点之间的距离用矢量之差的无穷范数表示。定义检验统计量

3.2.1 实验前后实验组、对照组学生的跳高成绩对照（见表2）由表2调查结果显示：在实施此项教学方法前，实验组和对照组的跳高运动成绩没有显著性差异，即实验组和对照组的运动水平是一致的，通过模块教学试验后，实验组的跳高成绩具有显著性差异，特别是男生的跳高成绩更是具有非常显著性差异。表明此教学方法对提高学生的跳高成绩是有效的。

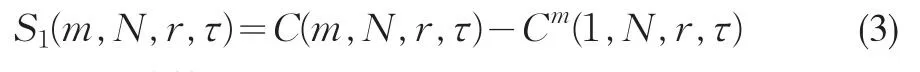
式(3)的计算过程为：将时间序列x={xi|i=1,2,…,N}分解成τ个互不重迭的子序列，τ为重构时延，即

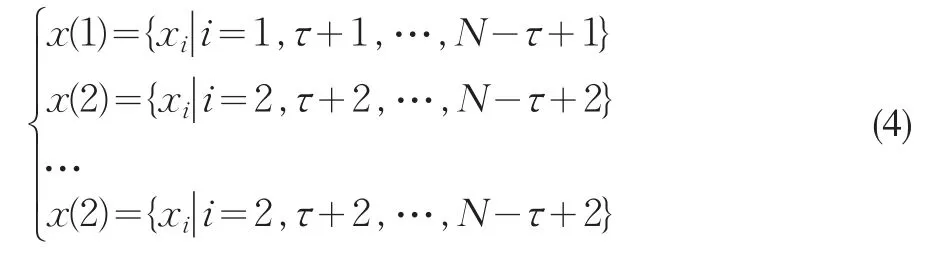
式(3)定义的统计量采用分块平均的策略，即

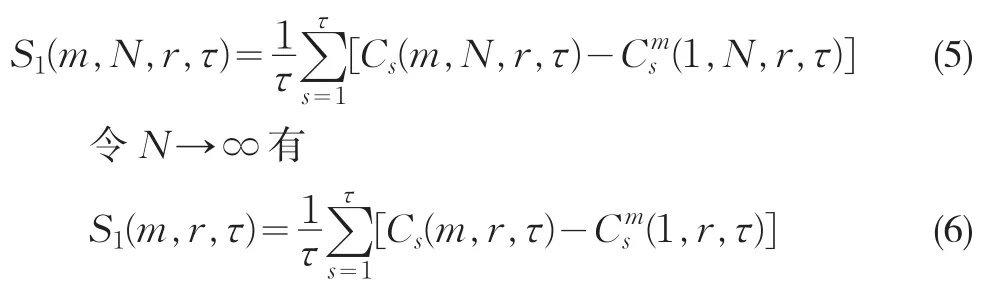
对固定的m和τ，当N较大时，S1(m,r,τ)反映了时间序列的自相关特性，仿照求时延的自相关原理，最佳时滞τ可取S1(m,r,τ)的第一个零点，或取S1(m,r,τ)对所有半径r相互差别最小的时间点，此时表示重构相空间中的点最接近均匀分布，重构吸引子轨道在相空间完全展开。选择最大和最小的两个半径r，定义差量

本文选取1990年1月到2011年7月的中国CPI指数，共259个数据，得到时间序列x={xi|i=1,2,…,N}，其中N=259。对该序列采用C-C法确定最佳嵌入维与时滞，分别选取m为2～10，r为δ/2～ 2δ，t为200，进行计算，由图1可得最终结果，即最佳嵌入维m为7，时滞τ为19。

2 最大Lyapunov指数的计算

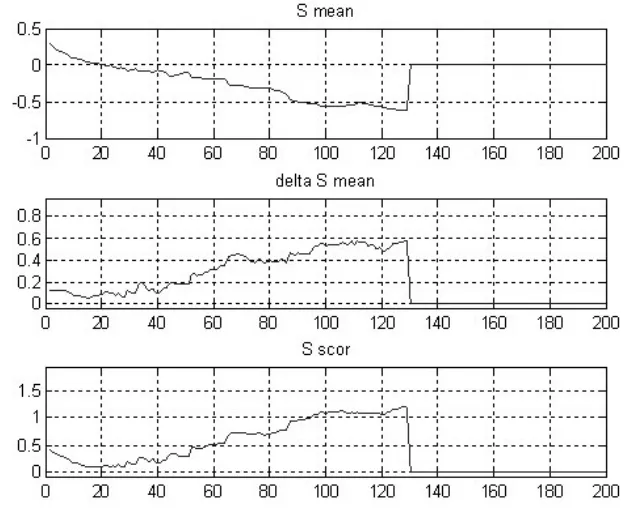
图1 C-C法计算结果

Lyapunov指数是指轨道收敛率或发散率，是研究混沌的重要参数，其最大Lyapunov指数为正，就可判断该系统为混沌。Wolf等提出了基于相轨线、相平面、相体积等的演化来估计最大Lyapunov指数[6]，其算法如下：对于混沌时间序列x={xi|i=1,2,…,N}，以嵌入维m，时滞τ，则重构相空间为(1)式所示。

取初始点X(i0)，设其与最邻近点X0(i0)的距离为L0。追踪这两点的时间演化，直到i1时刻，其间距超过某给定值，保留X(i1)，并在X(i1)邻近另找一个点X1(i1)，使得L1= |X(i1)-X(i0)|＞ε并且与之夹角尽可能的小；继续上述过程，直至X(i)到达时间序列的终点N。这时追踪演化过程总的迭代次数为M，则最大Lyapunov指数为

运用此方法，求得CPI时间序列的最大Lyapunov指数λmax=0.2553。

3 基于CBP算法的CPI预测

文献[4][5]表明，与BP神经网络相比，混沌神经网络CBP除了具备较强的非线性逼近能力以及自组织和分类概括的能力外,还具有混沌遍历的能力以防止陷入局部极小[7,8]。因此CBP网络的特性使得它适合预测混沌动力系统的时间序列。用于预测的神经网络结构如图2所示。

图2 CPI预测神经网络结构图

本文采用混沌BP混合学习算法，以梯度下降搜索算法快速收敛到局部最优,同时依赖混沌全局优化摆脱局部极小，最终收敛到全局最优。混沌的产生，采用Logistic方程：xn+1=μxn(1-xn)，n=0,1，…，N(0＜x0＜1)。若取μ等于4，则完全处于混沌状态且混沌变量xn在(0,1)范围内遍历。混沌状态具有对初始值极其敏感的特点,取不同的初始值可得到不同轨迹的混沌变量。具体步骤如下：

(1)在（-1,1）区间产生随机数赋BP神经网络初始权值。

(2)采用BP算法对神经网络权值进行学习,计算网络误差记为EBP,若学习后满足精度要求,此时网络权值向量记为W,则算法结束；否则,转入步骤(3)。

(3)经过BP学习后的权值W，进入以下混沌优化搜索。在区间（0,1）随机初始化混沌向量X0，且与权值向量W的维数一致，并置k=0。

(4)利用混沌变量Xk产生新权值向量（其中，ρ为常数），是新权值向量在以W为中心，ρ|W|为半径的（W-ρ|W|，W+ρ|W|）区间遍历计算神经网络误差记为ECBP；

(5)Xk+1=4Xk(1-Xk),k=k+1

(6)若网络误差ECBP满足精度，算法结束；否则，转入(7)

(7)比较 EBP和 ECBP的大小，若ECBP＜EBP，则令，转入步骤(2)，否则转入步骤(4)

设定算法条件：CPI原始序列经过相空间重构为145×7的矩阵，输入输出如图2所示。其中取107行作为训练样本，取19行作为测试样本，取10行作为预测样本。取目标误差0.0001，训 练 最大步数 3000，输入神经元个数等于饱和嵌入维数为7，隐层个数为20，输出层1。预测结果见表1和图3。

图3 预测误差

表1 CBP短期预测结果

4 结论及研究展望

本文通过将神经网络与混沌时间序列理论结合进行CPI预测，得到以下主要的结论：

（1）CPI时间序列的最大Lyapunov指数λmax计算结果大于零表明，CPI不是完全随机的行为，它受到诸多非线性因素的支配与控制，CPI的波动表现出一定的混沌规律。

（2）由图3预测结果可知，运用混沌理论建立的CBP神经网络CPI预测模型在短期内预测精度高，可行性强。如图3显示6个月内预测误差很小，超过6个月的误差急剧增加。这与混沌时间序列长期不可预测性的特征相符合，弥补了现有文献预测时间短或精度差的缺点；同时结果显示该模型可以作为CPI半年度预测。因此，本文对2011年8月到2012年1月做了短期预测（见表1）。

由预测结果可知，我国CPI指数同比增长率整体呈现下降趋势，到2011年12月份CPI可控制在3.63%，这与国家CPI控制目标4%基本相符合，说明国家采取抑制通货膨胀政策效应在8月份开始显现。但是，2012年1月份CPI同比增长率有小幅度回升，说明不稳定、不确定因素仍然较多，货币政策不能放松，可以实施差别存款准备金率，防止超调。积极的财政政策和稳健的货币政策仍然是国家宏观经济政策的基本取向。而企业在当前经济政策形势下，融资困难和成本上升是当前和未来面临的主要问题，企业需要进行制度创新，特别是中小企业可以通过兼并重组，从单个资本变成社会成本，增强抗风险能力。

本文所用模型不仅理论上可行，而且有很广的应用前景。由于受国家统计局提供的CPI数据所限，样本采样周期为一个月，但这并不影响模型的一般性。随着CPI研究的进一步深入，可以获取更短的采样周期。此外，该时间序列的噪声影响也是值得探讨的问题。

[1]孙博文,张本祥.中国股市波动的混沌吸引子的测定与计算[J].哈尔滨理工大学学报,2001,(6)

[2]陈玉海.我国CPI预测数量研究[D].中南大学硕士学位论文,2010,(9),

[3]王宇,李旭东,李自力.基于BP神经网络的我国CPI预测与对策[J].计算机科学,2009,(10)

[4]姚跃华,牛园园.基于RBF神经网络的CPI预测[J].计算机应用与软件,2010,(10)

[5]Takens F.Detecting Strange Attractors in Turbulence.Dynamical Sys⁃tems and Turbulence,Lecture Notes in Mathematics[C].Berlin:Spring⁃er-Verlag,1981,898.

[6]A.Wolf.j.B.Swift,H.L.Swinney,J.A.Vastano.Determing Lyapunov Ex⁃ponents from a Time Series[D].Physica 16D,1985.

[7]夏景明,肖冬荣.基于Lyapunov指数和CBP的混沌时序预测模型[J].统计与决策,2007,(16)

[8]李祥飞,邹恩,张泰山.一种新型的混沌BP混合学习算法[J].中南工业大学学报,2003,(5)