基于系统动力学的我国地价与房价关系及对策研究

戴颖杰，周奎省

（西安交通大学 经济与金融学院，西安 710061）

1 问题的提出

由美国房地产泡沫破灭引发的世界金融风暴，使全球正面临自上世纪30年代“大萧条”以来最严重的金融危机。这使房地产价格再度成为各国关注的焦点。近一年来中国房地产价格在经过几年的持续上涨后迅速下跌又迅速高涨。土地市场中“地王”也频频出现。住宅价格过高可能引发房地产泡沫已经引起了社会各界的关注和忧虑。住宅价格过高是否由于地价过高而引起，地价和房价之间存在什么关系？

从现有的研究可见，不管是理论分析和是实证分析，关于二者之间的关系都没有比较统一的观点。就国内实证分析而言，采用的数据绝大多数是土地和房屋销售季度价格指数，运用的方法实质上都是格兰杰因果检验。但是，实证分析的结论却大相径庭，甚至同一作者的分析结论也存在冲突。如宋勃（2007）认为，在考虑通货膨胀的条件下，短期房价对地价没有影响，而地价是房价的Granger原因；其（2009）却认为在考虑通货膨胀的条件下，短期地价对房价没有影响，而房价是地价的Granger原因。

为什么在采用的数据和分析方法大致相同的情况下，分析结果却大相径庭？上述计量经济模型分析当中，到底哪些模型设置合理，结论相对可靠？哪些模型对我国目前的房地产宏观调控具有借鉴意义？遗憾的是，目前国内关于计量模型的比较与评价方面的研究相对薄弱，有关地价和房价关系的计量模型比较与评价尚未发现。本文主要目的在于对国内有关地价和房价关系的计量模型运用系统动力学进行比较与评价，分析哪些模型比较合理，进而说明其结论相对可靠，试图对计量模型比较与评价提供了一种新的思路，从而对我国房地产宏观调控提供决策依据。

2 运用系统动力学的优点及指标设定

2.1 运用系统动力学的优点

计量经济学关于模型比较的方法分为嵌套模型和非嵌套模型两大类。对于嵌套模型的选择，主要利用F统计量进行排除性约束检验，相对来说比较简单。但是，在实际当中面临的绝大多是非嵌套模型。对于非嵌套模型的选择常用是利用Rˉ2、人工综合模型法、J统计量检验法、JA统计量检验法和COX检验法等。但是上述非嵌套模型的选择方法各自存在这缺陷。其中，Rˉ2在模型因变量形式不同时，无法得出比较选择的结果；人工综合模型法存在模型参数无法完全识别的困难；J统计量检验法在有限样本下通常是不精确的，且往往存在很严重的过度拒绝问题；JA统计量检验法要求比较的模型都满足古典正态线性模型假设的所有条件，使用条件过于苛刻；同时，以上三种方法的检验结果存在比较模型都被拒绝或者都不拒绝的情况，可能无法得出确定的选择结果。COX统计量只有在渐进正态下才是有效的，且计算非常困难，在必须进行一系列的回归之外，上述计量模型选择方法无法对模型本身是否正确做出判定。

所以笔者认为，如果利用系统动力学对计量模型进行比较评价，可以克服计量经济学模型选择方法存在的弊端。第一，系统动力学对系统的评价主要从稳定性、准确性和快速性三个方面进行，而且有统一的评判指标，这样即使模型的变量个数、形式等有所不同，根据统一的评判指标也可以对系统做出比较与评价，可以克服计量经济学中用Rˉ2对模型进行比较是存在的困难；第二，该方法不存在参数无法识别的问题；第三，该方法使用的限制条件较少，使用范围较为广泛；第四，利用MATLAB进行计算仿真也简单易行；最后，该方法还可以识别出模型本身是否正确恰当。

2.2 运用系统动力学的指标设定

系统动力学是一门分析研究信息反馈系统的学科，是一门交叉、综合性的学科，其主要吸收了控制论、反馈论、信息论、非线性系统理论及大系统理论等学科的内容。系统动力学对于线性定常系统的性能评价，主要从以下二个方面进行：

（1）稳态评价指标。①系统的稳定性。这是系统动态特性中最重要的指标，也是设计和评价一个系统的前提条件。对于经济系统而言，稳定性意味着当时间t趋于无穷大时经济系统处于均衡状态。系统动力学中对系统稳定性的检验对应于计量经济学中的协整检验。协整在计量经济学中意味着经济变量之间存在长期均衡关系；②稳态误差。在稳态时，如果系统的输入量和输出量不能完全吻合，则称系统具有稳态误差。这个误差表示了系统的精确度。在系统动力学中，通常误差控制在2%之内，则意味着系统的精确度已经达到了满意的程度。

（2）瞬态评价指标。这是在系统稳定的前提下，衡量系统过度过程中动态性能的重要指标。其具体包括以下指标：①上升时间，是指系统响应曲线从稳态值的10%上升到95%所需要的时间；②峰值时间，是指系统响应曲线到达第一个峰值所需要的时间；③超调量，是指峰值和稳态值的差与稳态值之比；④调整时间，是指系统响应曲线有开始时刻进入到稳态值上下两个值所规定的范围内而且不再越出这个范围所需要的时间。限定该范围的两个值通常是稳态值的上下2%。

这些指标体现了系统的稳定性、准确性和快速性。其中稳定性指标和系统超调量分别考量了系统的绝对稳定性和相对稳定性；稳态误差则考量了系统的准确性；上升时间、调整时间和峰值时间则表达了系统的快速性。

3 典型计量模型的系统动力学比较与评价

从国内地价和房价关系的实证分析的回顾可见，现有研究实质上运用的都是格兰杰因果检验法。不过，已有研究在运用这一方法时有所差异，大致可分为单方程格兰杰因果检验、基于VAR模型的格兰杰因果检验和基于误差修正模型的格兰杰因果检验。其中以基于VAR模型的格兰杰因果检验的研究较多。本文从这三种方法中选取四个具有代表性的模型进行比较与评价。其分别是高波，毛丰付（2003）（①号模型）、龙海明，郭微（2009）（②号模型）、周京奎（2006）（③号模型）和马智利，阳廷燕（2008）（④号模型）。其中①号模型代表了单方程检验，②号和③号模型代表了基于VAR模型的格兰杰因果检验，④号模型代表了基于误差修正模型的格兰杰因果检验。

3.1 典型计量模型所确定系统的性能分析

3.1.1 ①号模型所确定系统的性能分析。①号模型为：

其中，X代表土地价格，Y代表房屋价格。

（1）方程(1)所给系统的稳态性能分析。设Y=y(t)，X=x(t)，t=0,1,2…∞。即设X和Y都是时间t的函数。据此，可以将方程(1)改写为时域方程的形式，即

①稳态性能分析。设y(t)的Z变换为y(z)，x(t)的Z变换为x(z)。对方程(3)两边同时进行变换得：

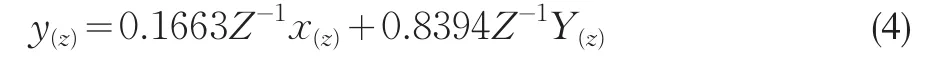
设系统的闭环传递函数为G（z）。通过方程(4)可得系统的闭环传递函数如下：

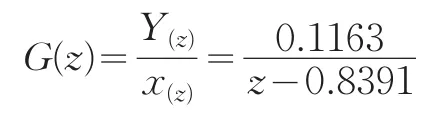
根据系统动力学原理，系统闭环传递函数的极点位于Z平面单位圆周的内部时系统稳定。运用MATLAB7.0绘制系统的零极点图如下：

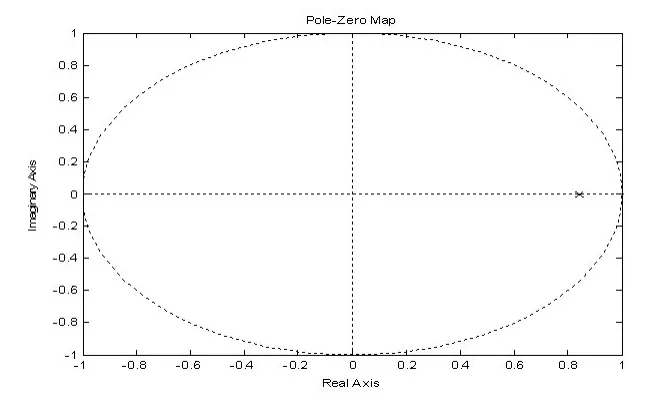
图1 方程(1)系统的零极点图

从图1可见，极点（图中符号“×”代表极点）位于单位圆周内，因此系统稳定。在单位阶跃输入下，可以计算出系统的稳态误差e(∞)。

②瞬态性能分析。根据方程(1)系统的闭环传递函数，运用MATLAB7.0得出系统在单位阶跃输入下系统的响应曲线如图2。图2中，从左向右的三个实心圆点分别为系统瞬态相应的上升时间、调整时间、系统的峰值时间及最大超调量。运用MATLAB7.0可以得出该系统的上升时间tr=12.5季度；调整时间ts=22.4季度；峰值时间tp=35季度；最大超调量Mp=0。

图2 方程(1)系统的单位阶跃响应曲线

（2）方程(2)系统的特性分析

将方程(2)改写为时域方程的形式，即

设Yt的Z变换为Yz，Xt的Z变换为Xz。对方程(5)两边同时进行Z变换得：

通过方程(6)可得出系统的闭环传递函数如下：

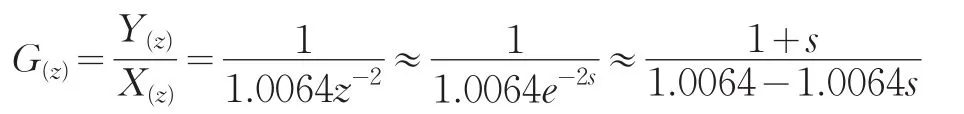
根据系统动力学原理，系统稳定的充分必要条件是系统闭环传递函数的极点位于复平面的左半平面。该系统的零极点图如下：

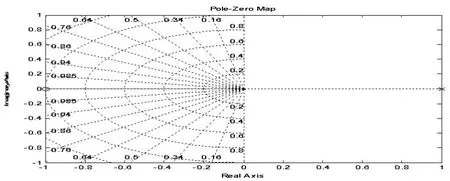
图3 方程(2)所给系统的零极点图

由于图3可见，系统的极点位于复平面的右半平面，所以方程(2)给出的系统是不稳定的。这一分析结果也与曾向阳和张安录的结论一致。这说明①号模型的第二个计量方程有误。由于系统的准确性能和快速性能建立在系统稳定的前提条件之上。既然方程(2)给出的系统是不稳定的，所以不能也没有必要继续考察该系统的准确性能和快速性能。

3.1.2 ②号模型所确定系统的性能分析。②号模型为：

其中：LHP=ln(HP)（房价指数的自然对数），LLP=ln(LP)（地价指数的自然对数）。

（1）方程(7)所确定的系统性能分析。设LHP=y(t)，LLP=x(t)，t=0,1,2…∞。即设LHP和LLP都是时间t的函数。据此，可以将方程(7)写为时域方程的形式，即

设y(t)的Z变换为y(z)，x(t)的Z变换为x(z)。对方程(9)两边同时进行Z变换得：

显然，方程(7)所给出的系统是反馈闭环系统。根据方程(10)以求可出给系统在单位阶跃输入下的闭环传递函数为：

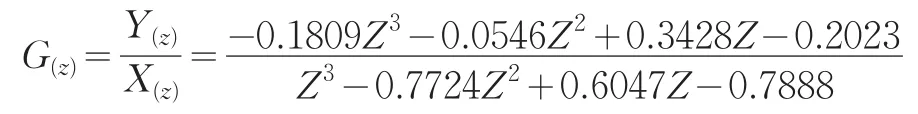
系统零极点图如下：

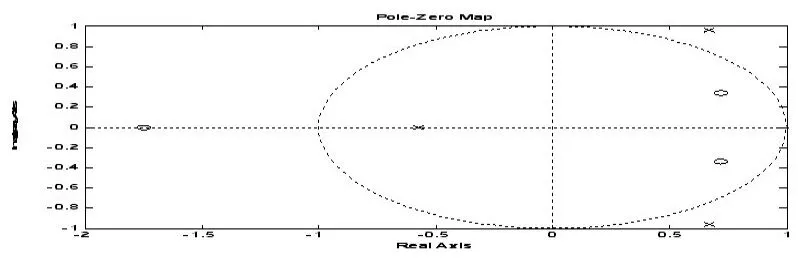
图4 方程(7)所给系统的零极点图

从图4可见，有两个极点（图中符号“×”代表极点，符号“○”代表零点）位于Z平面单位圆周的外部，因此系统不稳定。所以，方程(7)给出的系统是不稳定系统。既然方程(7)给出的系统是不稳定的，所以不能也没有必要继续考察该系统的瞬态性能。

（2）方程(8)所确定的系统性能分析。首先将方程(8)改写为时域方程为：

①稳态特性分析。显然，这也是一个反馈闭环系统。在单位阶跃输入下，该系统的闭环传递函数为。同样，用MATLAB7.0可以绘出零极点图如下：

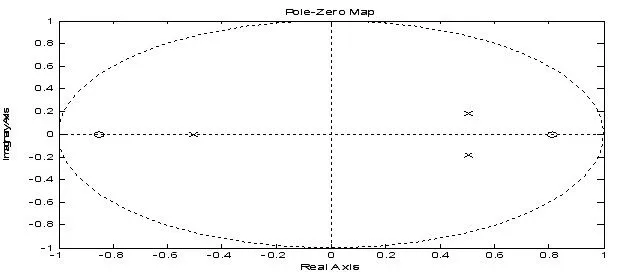
图5 方程(7)所给系统的零极点图

从图5可见，有三个极点均位于Z平面单位圆周内，因此系统稳定。在单位阶跃输入下，系统的稳态误差e(∞)计算如下：

②瞬态性能分析。运用MATLAB7.0得出系统在单位阶跃输入下系统的响应曲线如下：

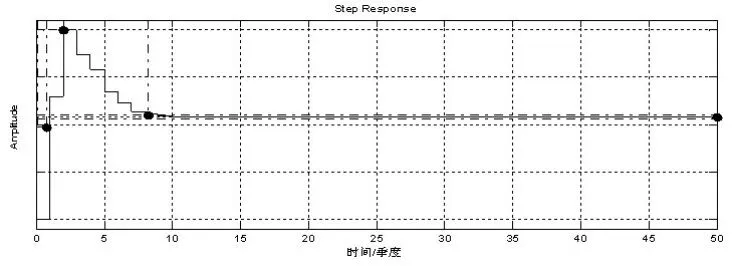
图6 方程(7)所给系统的单位阶跃响应曲线

从图6可看出，该系统的上升时间tr=0.665季度；调整时间ts=8.22季度；峰值时间tp=2季度；最大超调量Mp=85%。

3.1.3 ③号和④号模型所确定系统的性能分析。本文在此给出③号和④号模型所确定系统的性能分析结果。

表1 ③号和④号模型所确定系统的性能

3.2 典型计量模型的比较与评价

(1)地价对房价影响系统。通过上述典型模型性能分析可见：第一，从稳定性指标看，②号计量模型所确定的系统不稳定，所以该模型设定有误；第二，根据准确性指标，④号模型的稳态误差最小，其次是③号和②号模型；第三，从模型的快速性指标看，③号模型所确定系统的上升时间为3.3季度，调整时间为4.97季度，均小于①号和④号模型。所以，③号模型所确定的系统反应速度最快；第四，虽然④号模型的准确性最高，但其反应速度大大低于③号模型，而③号模型的准确性之比④号模型差0.1%。因而，综合考虑模型的稳定性、准确性和快速性，相较而言③号模型的性能较好。

(2)房价对地价影响系统。从上文对模型性能的分析可以发现：第一，①号和④号模型所确定的系统不稳定，因而可以判定这两个模型设定有误；第二，②号和③号模型的稳态误差分别为29.45%和6.11%，因而③号模型的准确性较好；第三，从上升时间和调整时间来看，②号模型远远小于③号模型，因而②号模型的反应速度要好于③号模型；第四，②号模型的最大超调量为85%，这说明②号模型的相对稳定性较差；第五，从系统的稳定性和准确性来看，③号模型要好于②号模型，从系统的快速性看，②号模型却要好于③号模型。但是，由于②号模型的最大超调量为85%，说明该模型所确定的经济系统震荡幅度较大。因而，综合权衡系统的三个性能，③号模型相对比较理想。

因此从系统的稳定性、准确性和快速性三个方面综合考虑，笔者认为在以上四个典型模型中，③号模型较为理想，根据该模型得出的实证分析结论也较为可靠。

4 结论及对策建议

关于地价和房价关系的实证分析，国内的研究基本上采用的是格兰杰因果检验。根据具体方法的不同，本文将已有研究分为基于单方程、VAR和误差修正模型的格兰杰因果检验。

通过本文对典型模型所确定系统的性能分析可以发现，这些计量模型的准确性不高，达不到系统动力学的要求。这可能与样本容量有关。现有的关于地价和房价关系的计量经济模型，绝大多数采用季度数据，周期为一个季度。依据系统动力学原理，采样周期为1季度时，离散系统的时间跨度至少应为50个季度，即样本容量至少应为50。而现有的模型最大样本容量为41个季度的数据。Pierse和Snell也指出：修正的ADF单位根检验方法以及协整检验的E-G二步法，要求样本容量必须充分大，否则得到的协整参数估计量是有偏差的。

最后本文通过运用系统动力学对这三种方法的典型实证模型比较与评价，得出以下结论：基于单方程格兰杰因果检验所做出的地价和房价关系计量模型的性能最不理想；就本文具体分析的几个模型而言，③号模型即周京奎（2006）较理想。根据周京奎（2006）的实证分析，地价和房价的关系为：地价对房价并没有显著影响，而房价对地价有非常显著的影响。

根据实证结果，本文对我国房地产的宏观调控有如下对策建议：

(1)注重目前房地产宏观调控政策的延续性、稳定性和长期性。

地价对房价的基本构成、价位高低，具有很重要的作用。但就目前的房地产实际来看，几乎很少有开发商是按照成本来给楼盘定价。目前的房价除了要计算基本的开发经营成本之外，更多地考虑了眼下市场的供需情况、同类产品的房价水平，再结合对市场的冷热判断、对房价的预期和竞争需要等因素来定价。由此来看，地价只是决定房价的重要因素，而不是决定性的因素，地价低不一定房价就低，而在房价下降的时候，地价一般不会高，甚至还有可能出现流标现象，地价对房价并没有显著影响，而房价对地价有非常显著的影响。所以要注重目前房地产宏观调控政策的延续性、稳定性和长期性，从供求关系、市场预期等环节着手，继续通过限购、限贷等行政手段来降低开发商的期望利润水平，使房价回归到合理价位，从而促进房地产市场健康有序发展。

(2)构建房地产市场健康有序发展的长效机制。

比如试行房产税。房产税对市场的作用是长期的、市场化的、可持续性的，能有效保持调控政策的长期性和稳定性，防止政策和市场的大起大落，也能量化地调节高、中、低不同收入群体的住房需求，使得房地产调控更有针对性，同时也增加地方政府财政收入，加大地方政府对调控的积极性和主动性；又比如可以加大保障房建设，使其对整个房地产市场的房价产生挤压作用，合理地调整供求关系；同时依法运用土地增值税、耕地占用税、空地税等税收手段，优先购买权、无偿回收闲置土地等行政权以及其他金融、法律等多种措施规范市场参与者的行为，防止土地投机、粗放用地和闲置土地不合理行为，调整供地结构、公开供地信息和打击囤地炒地违规行为，还土地作为生产要素的本来面目。

(3)树立科学的住房消费观念。

由于受到传统文化的影响、超前消费的宣传、财富增值的诱惑，房地产市场上低龄化、超前性、恐慌性购房现象层出不穷，在一定程度上为房价高涨起到推波助澜的作用。所以政府应引导公众树立科学的住房消费观念，使住房消费呈现出一种梯度消费的格局，合理调整市场供求关系，减少开发商的利润预期，抑制房价过快上涨，从而促进房地产市场的健康有序发展，促进和谐社会的构建。

[1]高波,毛丰付.房价与地价关系的实证检验:1999～2002[J].产业经济研究,2003,(3).

[2]周京奎.城市土地价格波动对房地产业的影响—1999～2005年中国20城市的实证分析[J].当代经济科学,2006,(7).

[3]宋勃,高波.房价与地价关系的因果检验:1998-2006[J].当代经济科学,2007,(1).

[4]马智利,阳廷燕.中国房价与地价关系的数据检验[J].重庆工学院学报(社会科学),2008,(9).

[5]宋勃,刘建江.房价与地价关系的理论分析与中国经验的实证检验:1998～2007[J].中央财经大学学报,2009,(9).

[6]龙海明,郭微.基于VAR模型的我国房价与地价动态计量分析[J].经济数学,2009,(6).

[7]J.M.伍德里里奇.计量经济学现代观点[M].费剑平,林相森译.北京:中国人民大学出版社，2003.

[8]罗素.戴维森，詹姆斯.G.麦金农.计量经济理论和方法[M].沈根祥译.上海:上海财经大学出版社，2006.

[9]威廉.H.格林.计量经济分析（第五版）[M].费剑平译.北京:中国人民大学出版社，2007.

[10]王其潘.高级系统动力学[M].北京:清华大学出版社，1994.

[11]钟高峥.我国房市价格驱动主因分析[J].求索，2010,(6).

[12]曾向阳,张安录.基于Grange检验的地价与房价关系研究[J].中国土地科学，2006,(4).

[13]Pierse,R.G.,Shell,A.J.Temporal Aggregation and the Power Oftests for Unit root[J].Journal of Econometrics,1995,(65).