基于动态规划的铁路三维空间智能选线方法*

蒲 浩，赵海峰，李 伟

(1．中南大学土木工程学院，湖南 长沙410075;2．高速铁路建造技术国家工程实验室，湖南长沙410075)

国内外的路线优化研究从平面优化、纵断面优化和平纵联合优化3个方向进行。平面线形优化的目的在于尝试使用系统的数学方法，利用计算机辅助技术找出最优线形。平面优化时，主要采用通过寻求平面交点位置后依规范插入曲线的方法。目前国外主要采用的方法有变分法、网络优化法、动态规划法和遗传算法［1］。进行平面线形设计后，再配合平面线形进行纵断面设计。纵断面线形的数学描述相对简单，早期纵断面线形优化设计主要是在假设平面线形已知的情况下，研究如何以各种数学模式描述并优化纵断面线形。纵断面线形优化常见的几种方法有枚举法，动态规划法，线性规划法、梯度投影、降维法和遗传算法［2－3］。空间线形优化采用的方法有动态规划法、随机搜索法、两阶段优化法和遗传算法。其中，变分法得到的优化结果具有全局优化和连续性的特点，但由于目标函数是有不连续性的各项费用(如占地费用)组成，因此，方法的假设并不符合实际情况，建立的目标函数不适合不连续因子，会出现局部收敛现象。网络优化算法由于要计算网格间的连通费用，如果缺乏GIS系统的支持，其费用区划分以及网格连通费用计算量非常大，而且输出结果不平滑，无法完成连续空间的搜索。线性规划法不适合非线性目标函数，仅能对受坡度和曲率限制的有限的点进行优化。随机搜索法以德国的EPOS－1程序为典型代表，此方法计算模型复杂，容易导致局部收敛，不易处理不连续费用情况［3］。近年来，随着现代优化技术与地理信息科学的发展，Jong 等［1，4－8］基于遗传算法构建了智能路线设计的框架。遗传算法虽已被证实适合于大规模复杂非线性优化问题的求解，但前期进化易早熟和后期进化速度缓慢是其最大的缺点［9－10］，而且遗传算法并不能保证达到全局优化，它仍然可能陷入局部极值的陷阱［11］。因此，有待寻求性能更好的算法来求解路线优化问题。由于选用动态规划法解决平纵面优化比较理想，因此得到了比较广泛的应用［12］，如美国麻省理工学院的空间线形选线程序OPTLOC、法国的平面线形优化程序APPOLON、丹麦的道路纵优程序以及我国交通部重庆公路研究所和重庆交通学院联合研制的 OPTSLD－2程序等［13］。该方法通常与网络优化结合，将线路优化视为连接起终点的最短路径问题，具有算法简单、理论完备、能够搜索到全局最优的特点［1］。另外，应用动态规划法，使得最优化问题数学模型的建立及约束条件的处理变得非常容易，从而使该模型具有比基于偏导数最优化方法的其他模型易于实用的优点［13］。但在以往动态规划的研究中，也存在将连续折线等非实用线形近似代替线路的问题。为此，本文作者提出一种基于动态规划法三维空间智能选线方法。在动态规划中直接采用更符合线路实际的“直线—曲线—直线”线形，在三维空间中搜索出符合平纵约束的全局最优和较优方案。算法实现简单，稳定性好。

1 目标函数和约束条件

在三维空间优化问题中，一般来说交点不包括线路的起终点，因为它们是已知的、不变的。缓和曲线长和竖曲线对线路的位置影响不大，这里不考虑平面缓和曲线和竖曲线的具体设计，在优化时只在夹直线的约束条件下预留缓和曲线位置即可［14］。以线路平面交点位置坐标、曲线半径和纵断面设计标高为设计变量，以线路设计规范及其他技术条件为约束条件，以换算工程费为目标函数，则铁路三维空间优化问题可以归结为求解下述非线性规划问题:

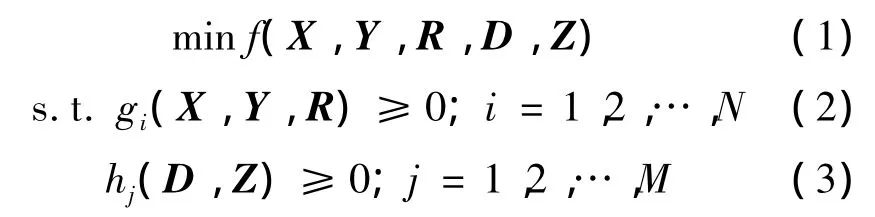
1．1 设计变量

X= ［x1，x2，…，xN］T，Y= ［y1，y2，…，yN］T，R= ［R1，R2，…，RN］T分别为平面交点坐标向量和曲线半径向量，N为平面交点个数(不含起终点)。

D= ［d1，d2，…，dM］T，Z= ［z1，z2，…，zM］T，为相应的纵断面变坡点里程向量和标高向量，M为纵断面变坡点个数。

1．2 目标函数

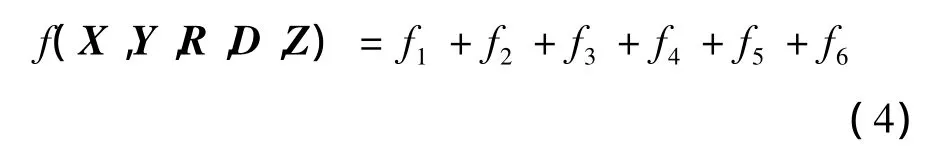
其中:f1为土石方工程费用;f2为桥涵费用;f3为隧道费用;f4为挡墙圬工工程费;f5为换算运营费、用地费;f6为与线路长度有关的轨道、通信设备等费用。

1．3 约束条件

式(2)中gi(X，Y，R)≥0为平面约束，主要包括:

①曲线半径不得小于允许的最小曲线半径值:Ri≥Rmin;

②夹直线长度(包括预留缓和曲线)满足规范要求:LJi≥LJmin;

③圆曲线长度(包括预留缓和曲线)满足规范要求:LYi≥ LYmin。

④必须经过的点、必须绕避的自然保护区或不良地质地区等其他几何约束。

式(3)中hj(D，Z)≥0为纵面约束，主要包括:

①选用技术标准限制:坡度限制、坡长限制等;

②标高限制:起终点衔接标高、路线通过固定标高点、路线标高必须限制在界定范围以内等。

2 三维动态规划模型的建立和求解

2．1 三维空间网格划分

首先对线路可能经行的区域进行三维空间网格划分。如图1所示。

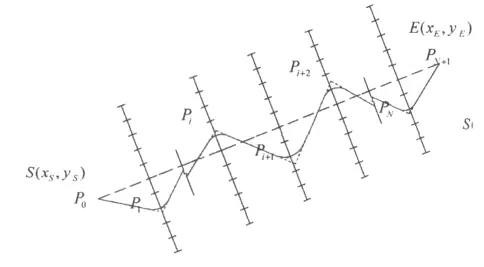
图1 三维网格的平面投影Fig．1 Plan of the search grid

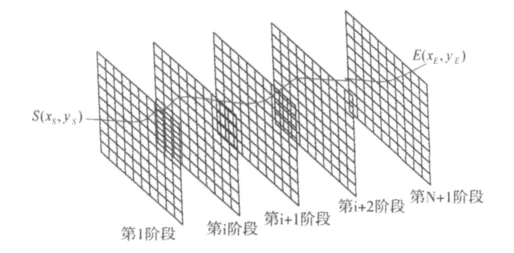
图2 三维搜索网格Fig．2 A 3D search grid

假设 S(xS，yS)、E(xE，yE)分别为路线的起点和终点，线段为起终点连线。假定用N个垂直面 A1，A2，…，Ai，…，An等分线段，则这些垂直面与路线交于 N 个不同的三维点 P1，P2，…，Pi，…，PN。假设每个垂直面上的点个数分别为 m1，m2，…，mi，…，mN。并规定线路与每个垂直面的交点必须在这些三维网格点中选择，即Pi必须在面Ai上的 mN个三维网格点 Pi，1，Pi，2，…，Pi，mi中选择，如图2。这N个垂直面将线路划分为了N+1个区间。

2．2 线路平面的生成

为了使三维搜索网格能更好的控制线路的走向，这里将每个垂直面上可选的三维点视为线路圆曲线的曲中点，而非线路的交点或链路折点。因而，由此选出的线路直接是符合线路要求的“直线－曲线－直线”的平面线形，而非由连续折线所组成的非实用线形。根据规范要求对每个圆曲线配置最小曲线半径为初始半径，即

R0= ［Rmin，Rmin，…，Rmin，…，Rmin］T

若令起点 S(xS，yS)=P0，终点 E(xE，yE)=PN+1，则P0，…，PN+1这N+2个点的选择就决定了1个线路的平面线形。

2．3 两点间线路纵断面的自动生成

一般来说，变坡点的个数和平面交点的个数并不相同，相邻2个曲中点间线路所对应的纵断面设计线也并不一定是单一的坡度，即任何2个曲中点之间的纵断面设计线应该是和地形相适应的。因此，本文将平顺地面线与最小二乘法相结合，研究了一种自动生成优化纵断面的方法，以快速决定线路上两点之间的纵断面设计线。即利用平顺地面线一阶差商反号处的里程作为坡段划分的界限值，从而可以获得不同的坡段划分方案，再采用最小二乘原理拟合直线获得坡度线。最后进行约束检验和纵坡调整。

2．3．1 地面线平顺

利用计算机寻求变坡点的位置，其实质就是寻求地面线走势发生改变的位置。原始地面线是一条不规则的锯齿状折线，这里采用屋架函数对地面线进行圆顺。设纵断面地面线有n个中桩，Xi，Yi(i=1，2，3，…，n)分别为其里程和地面高程，用屋架函数进行平滑的公式为［15］:

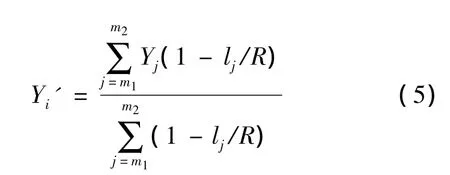
式中:R为平顺半径(m)，一般取最小坡段长;m1和m2为计算i点的平顺高程时将屋架函数中心置于i点，在函数2R范围内中桩起止序号;lj为j号中桩距i号中桩的距离(m)，lj=Xi－Xj;Yj为j号中桩的地面高程(m)。

利用上述函数对地面线进行平顺处理时，改变平顺次数或平顺半径R，都会对最后得到的曲线产生较大的影响，平顺次数越大曲线越趋近于平缓，平顺半径R越大曲线越趋近于平缓［15］。本文根据线路等级采用不同的平顺半径R及不同的平顺次数。

2．3．2 变坡点个数的确定

确定变坡点位置，即选择曲线上的反弯点及曲率发生变化的点。经上述平顺处理所建立的地面模型并不完全光滑，其一阶倒数并不连续［16］。因此，需对平滑地面线进行三阶及一阶均差计算，以查找其反弯点和曲率变化点，从而确定坡段的划分。

(1)三阶差商计算:

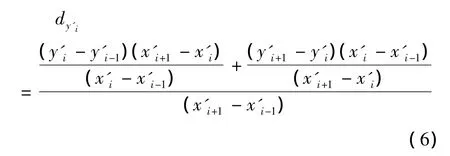
当 i=1 时，dy′1=(y′2－ y′1)/(x′2－ x′1);当i=n 时，dy′n=(y′n－ y′n－1)/(x′n－ x′n－1)。

经上述差商后，平滑曲线呈近似折线，需进一步进行一阶差商处理。

(2)一阶差商计算:

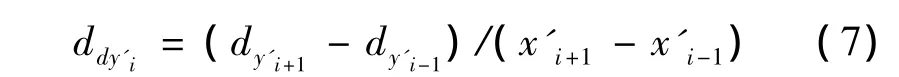
当 i=1 时，ddy′1=(dy′2－ dy′1)/(x′2－ x′1);当i=n 时，ddy′n=(dy′n－ dy′n－1)/(x′n－ x′n－1)。

经一阶差商处理后，差商值反号的点即为折线斜率发生变化的点，也就是平滑地面线的反弯点，以此划分线路坡段是最符合地面线起伏情况的。因此取一阶差商值反号处的里程为变坡点的分段里程。再对该方案的变坡点进行处理，删除不满足最小坡长的坡段，从而确定变坡点的个数。

2．3．3 变坡点位置的确定

为使所生成纵断面方案的工程数量最小，采用最小二乘原理拟合直线获得坡度线。设经平顺地面线某一坡段范围(Mi，Mi+1)内有m个地面线桩号点，设其中第i个桩号处的里程和高程分别为si和hi，设该坡段的直线方程为y=kx+a，根据最小二乘原理可得直线方程的系数k和a分别为［17］:

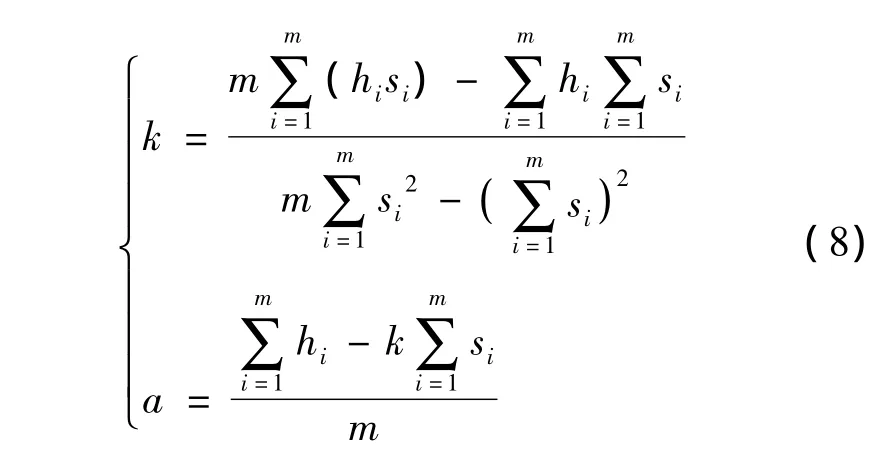
i=1，2，…，m。利用拟合所得相邻2条直线相交所产生的交点，得第i个变坡点坐标(Si，Hi)如下:

以依次连接各交点所得的折线为初始纵断面方案的坡度线，经约束处理后，根据规范要求配置适当的竖曲线即可得符合设计需要的纵断面设计线。

2．4 动态规划模型建立

(1)如图2中所示，N个垂直面将线路切分成N+1个区间，这N+1个区间可作为动态规划法决策中的 N+1个阶段:P0至 P1，P1至 P2，…，PN至PN+1。

(2)状态和决策。对第k阶段进行分析(其中k=0，1，…，N)，设第k阶段的状态变量用Sk表示，决策变量为Uk，决策集为Dk(Sk)，且令m0=1，则

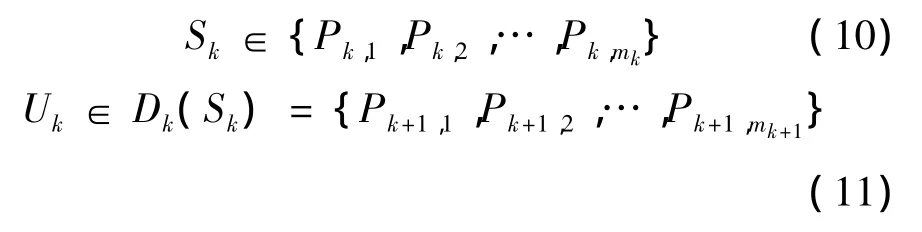
(3)策略。全过程策略记为为Q0，N，则

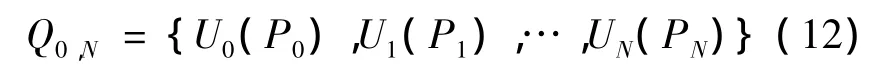
k 子过程策略记为 Qk，N，则

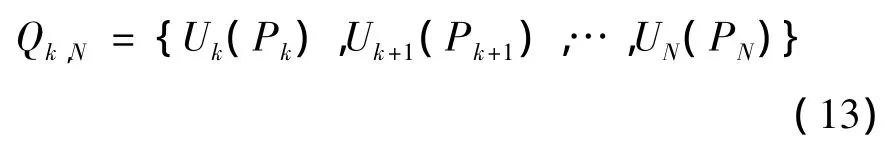
(4)状态转移方程为:

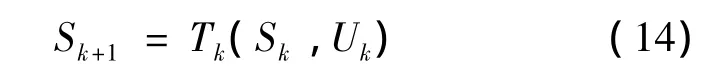
(5)指标函数和最优指标函数。若用fk(Pk，Pk+1)表示第k区间线路的综合费用，则阶段指标函数为:

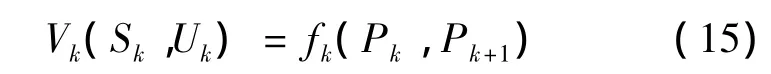
过程指标函数即铁路建造的综合费用为:

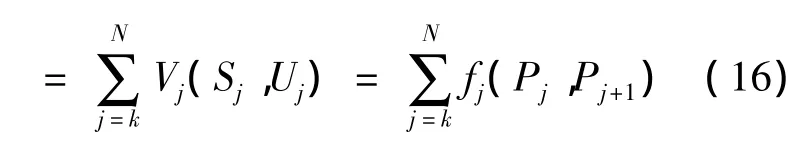
把过程指标函数Vk，N对k子过程策略 Qk，N求最优，得到关于状态Sk的最优值函数，即从第k阶段到终点PN+1的最小综合费用。记为fk(Sk)，则

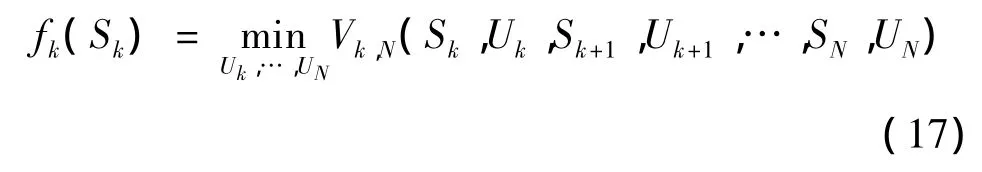
(6)动态规划基本方程。动态规划的递推方程为:

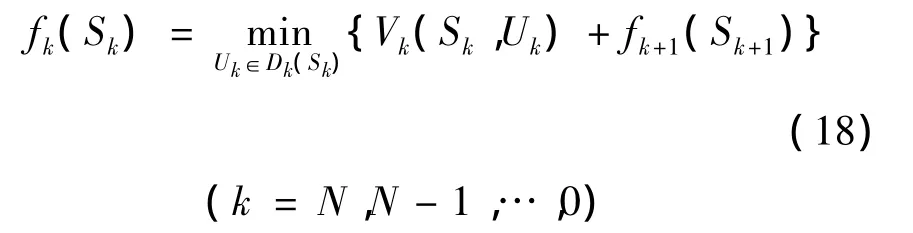
边界条件。

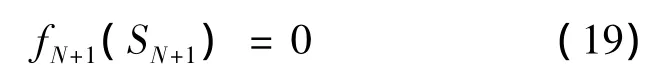
根据边界条件，从k=N开始，由后向前逆推，逐步求得各阶段的最优决策和相应的最优值，最后求出f0(S0)时，就得到整个问题的最优解。

2．5 第K阶段中2个状态间综合费用的计算

式(15)中的函数Vk(Sk，Uk)的计算方法如下。设第k阶段，在2个垂直面上选择的点分别为Pk(xk，yk，zk)和 Pk+1(xk+1，yk+1，zk+1)。首先，以 Rmin为初始半径，Pk点为圆曲线的曲中点反算出Pk和Pk+1之间的铁路线形。

(1)若该段线形不满足平面线设计约束条件，则令 Vk(Sk，Uk)=fk(Pk，Pk+1)= ∞ 。

(2)若该段线形满足平面线设计约束条件，对于该区间内的纵断面，当连接zk与zk+1的坡度大于允许最大坡度或小于允许最小坡度时，则该纵断面设计无论如何也不可能满足坡度约束条件。同样，该区间的线路设计方案综合费用也按无穷大数来对待。令 Vk(Sk，Uk)=fk(Pk，Pk+1)= ∞ 。

(3)若不属于上述2种情况，则对该区间的线路按纵断面自动生成方法自动生成相应的纵断面，自动配置桥梁、隧道等，并按式(4)计算该区间线路的目标函数f，即为第k阶段此方案的 Vk(Sk，Uk)。

2．6 模型求解

根据上述的动态规划基本方程式(18)，对所有的状态变量Sk，按K=N，N －1，…，0的顺序计算各个fk(SK)的值，最终求取f0(S0)即为起点P0到终点PN+1的最小代价函数。根据各阶段的状态转移方程Sk+1=Tk(Sk，Uk)得到全过程策略Q0，N={U0，U1，…，UN}，即得到了整体最优的线路方案。

2．7 双向搜索获得线路方案群

动态规划的实质是记忆化搜索。因此，对于从终点到起点的搜索过程。根据动态规划最优子结构的性质，第k阶段的决策过程中，状态变量Sk某一个可选节点 Pk，j(k=1，2，…，N+1，j=1，2，…，mk)都记录了从当前三维节点到终点的最小代价函数:

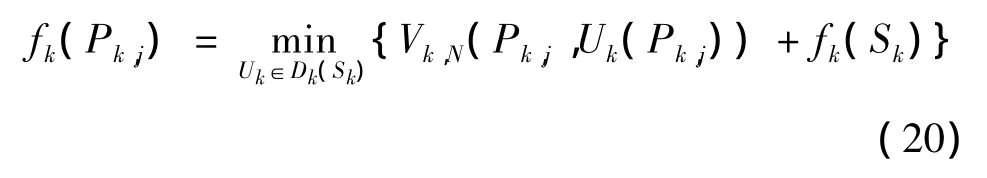
和从该节点到终点的最优路径:

对于从起点到终点的搜索过程，Pk，j点记录了从该节点到起点的最小代价函数:

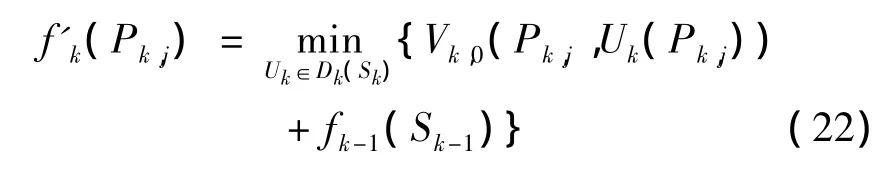
和从该节点到终点的最优路径:

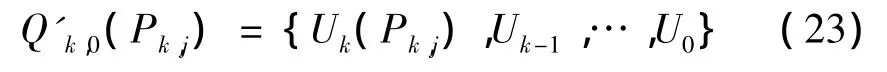
定义符号f(Pk，j)=fk(Pk，j)+f′k(Pk，j)，Q(Pk，j)=Qk，N(Pk，j)+Q′k，0(Pk，j)，则有:

(1)f(Pk，j)为连接起终点并且经过该三维网格点Pk，j的最小代价函数。

(2)为连接起终点并且经过该三维网格点Pk，j的最优路径。

证明:假设存在经过点Pk，j有代价函数更小的路径，该路径从Pk，j到起点和终点的代价函数分别设为 fQD(Pk，j)和 fZD(Pk，j)，并 且 有 fQD(Pk，j)+fZD(Pk，j)＜ f(Pk，j)。根据动态规划最优子结构的性质，有

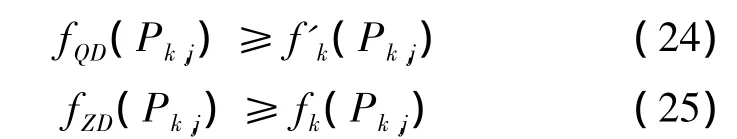
将由(24)和(25)相加，得:

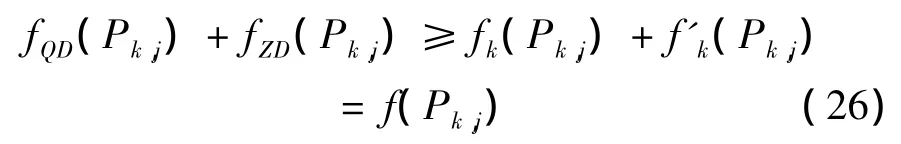
与假设 fQD(Pk，j)+fZD(Pk，j)＜ f(Pk，j)矛盾。结论得证。

采用双向的动态规划搜索，将每个网格点Pk，j计算经过该点的最小代价函数 f(Pk，j)，并按f(Pk，j)由小到大排序，即可得连接起终点的一组最优的线路方案群，然后，由状态转移方程Sk+1=Tk(Sk，Uk)即可得到对应的线路路径。

3 系统的开发与应用

应用本文所提出的理论和方法，开发了基于数字地球的铁路三维空间智能选线系统，系统包括集成的视窗管理、线路的自动搜索、方案的对比和评价、图表输出、线路方案的三维场景漫游等内容。

选取了某70 km的1条线路作为算例，计算结果表明:应用本文中提到的理论和方法能有效的搜索出一组优化的线路方案群，搜索出的线路方案能很好的绕避障碍物和适应地形。选线的结果可以作为工程设计人员提供前期设计参考，降低设计人员劳动强度和铁路的建造费用。三维可视化功能使规划设计人员能直观全面地掌握定线区域的地形、环境、地理、交通、地质等信息进行方案比选。

如图3所示，系统显示了1个绕避方案、1个隧道方案和1个人工设计方案。图中所示的绕避方案能够很好地适应地形并成功绕避山体，隧道方案接近人工选线的结果，但线路长度更短，工程造价更省。

图3 铁路三维空间智能选线系统Fig．3 Three dimensional spatial intelligent route selection system

4 结语

(1)基于三维空间的选线方法。即并不是通过不同的目标函数去独立地优化平面线设计和纵断面设计，而是着眼于以综合费用为目标函数来同时决定最优的平、纵断面设计线。

(2)符合实际的平面搜索线形。为了使三维搜索网格能更好的控制线路的走向，这里将三维网格点做为线路圆曲线的曲中点，而非线路的交点或链路折点。由此选出的线路是能很好反映线路特点的“直线－曲线－直线”的平面线形，而非由连续折线所组成的非实用线形。

(3)程序实现简单。动态规划法把一个复杂的选线问题转化为一系列单阶段问题，利用各阶段之间的关系逐个求解。对于较长的线路可以将其分成多个段落，在程序设计时利用多线程等技术同时搜索，最终得到整个区域的最优方案。并且动态规划法不需要得到目标函数的显式表达式，也不需要对目标函数求导。

(4)约束处理容易。文中提出的方法用三维空间网格点控制了线路的位置。对于不良地质地带、自然保护区等必须绕避区域的约束，只需要将三维空间网格中处于绕避区域的点设置禁忌，并将动态规划各阶段搜索中线路与绕避区域有交叉的方案造价设置为无穷大，就能很好地实现绕避。

(5)选线效率高。利用计算机一次性生成大量的备选方案，设计人员几个月甚至成年的工作量，最多几天便可完成选线的任务，大大提高设计效率。

(6)方案多样性好、效率高。系统最终生成的不是1个方案，而是1个包含绕避方案、架设桥隧方案等不同特点的最优方案群，可以为线路设计人员提供有价值的参考和比选，避免了由于设计人员主观因素而遗漏可行方案。

［1］Jong J C．Optimizing highway alignments with genetic algorithms［D］．Maryland:University of Maryland，1998．

［2］Eungcheol K，Jha M K，Bongsoo S．Improving the computational efficiency of highway alignment optimization models through a stepwise genetic algorithms approach［J］．Transportation Research:Part B，2005(39):339 －360．

［3］叶亚丽．公路智能选线与决策支持系统研究及开发［D］．西安:长安大学，2010．YE Ya-li．Researeh and development of highway alignment intelligent selection and decision support system［D］．Xi＇an:Chang’an University，2010．

［4］Jha M K．A geographic information systems－based model for highway design optimization［D］．Maryland:University of Maryland，2000．

［5］Jha M K，Schonfeld P．Integrating genetic algorithms and GIS to optimize highway alignments［J］．Transportation Research Record，2000(1719):233 －240．

［6］Jong J C，Jha M K，Schonfeld P．Preliminary highway design with genetic algorithms and geographic information systems［J］．Computer － Aided Civil and Infrastructure Engineering，2000(15):261 －271．

［7］Jha M K，Schonfeld P．A highway alignment optimization model using geographic information systems［J］．Transportation Research:Part A，2004(38):455 －481．

［8］Jong J C，Schonfeld P．An evolutionary model for simultaneously optimizing three－dimensional highway alignments［J］．Transportation Research:Part B，2003(37):107－128．

［9］刘好德，杨晓光．基于改进遗传算法的公交线网优化设计研究［J］．计算机工程与应用，2007，43(8):10 －14．LIU Hao-de，YANG Xiao-guang．Research on transit network design based on improved genetic algorithm［J］．Computer Engineering and Applications，2007，43(8):10－14．

［10］涂圣文，苏 州．基于GIS和遗传－粒子群的公路智能选线方法［J］．长安大学学报:自然科学版，2010，30(4):39－45．TU Sheng-wen，SU Zhou．Intelligent route selection of highway alignments based on GIS and hybrid genetic algorithm and particle swarm optimization［J］．Journal of Chang’an University:Natural Science Edition，2010，30(4):39－45．

［11］戴光明．避障路径规划的算法研究［D］．武汉:华中科技大学，2004．DAI Guang-ming．Research on algorithm for avoidance obstacle path planning［D］．Wuhan:Huazhong University of Science and Technology，2004．

［12］谷 克．遗传算法在公路路线智能决策系统中的应用研究［D］．西安:长安大学，2008．GU Ke．Study on the genetic algorithms’application in highway alignment intelligent decision system［D］．Xi＇an:Chang’an University，2008．

［13］冯 晓，谢远光．线形工程计算机辅助选线设计理论与方法［M］．成都:西南交通大学出版社，2008．FENG Xiao，XIE Yuan-guang．Alignment engineering computer aided design theory and methodology［M］．Chengdu:Southwest Jiaotong University Press，2008．

［14］李 伟，蒲 浩，彭先宝．基于方向加速法的铁路既有线平面重构优化算法［J］．铁道科学与工程学报，2009，6(3):47 －51．LI Wei，PU Hao，PENG Xian-bao．Existing railway plane line reconstruction algorithm based on direction acceleration method［J］．Journal of Railway Science and Engineering，2009，6(3):47 －51．

［15］谢春玲．基于改进遗传算法的铁路纵断面优化研究［D］．长沙:中南大学土木工程学院，2010．XIE Chun-ling．Study on railway profile optimizing system based on genetic algorithms［D］．Changsha:School of Civil Engineering，Central South University，2010．

［16］陈慧勇，路 伟．铁路线路纵断面计算机辅助设计及优化方法的研究与运用［J］．中国铁路，2002，15(6):49－50．CHEN Hui-yong，LU Wei．Study and application of computer aided design in railway track vertical section and its optimization［J］．China Railways，2002，15(6):49－50．

［17］Baker J E．Adaptive selection methods for genetic algorithms［J］．Proceedings of the 1st International Conference on Genetic Algorithms，1985:101 －111．