基于兴趣度的高职课程关联规则挖掘＊

董 辉

（亳州职业技术学院信息工程系，安徽 亳州 236800）

基于兴趣度的高职课程关联规则挖掘＊

董 辉

（亳州职业技术学院信息工程系，安徽 亳州 236800）

研究关联规则数据挖掘，讨论兴趣度的概念，设计基于此概念的算法.以高职成绩数据库为处理对象，分析课程间的关联规则，并以兴趣度为约束条件，剔除具有欺骗性的无效关联，挖掘一些合理可靠的课程间有趣的关联规则，从而为高职课程设置和教学大纲的修订提供参考，同时也验证了算法的有效性.

数据挖掘；关联规则；兴趣度；课程设置

高校各专业的课程设置，体现了相应专业人才培养目标、要求及人才培养规格等，因此在确保教学质量的过程中，课程是直接影响人才培养质量最关键、最活跃的因素，课程建设是核心内容，是教学质量的标志［1］.同一专业的各课程之间存在相关联性，如各课程的先后、内容衔接以及课程的专业权重等，因此，构建科学的课程体系和合理的课程设置是至关重要的.目前，每个高职院校都有自己的课程设置方案，但事实上很多高职院校在课程设置上存在不少问题，如相关课程的前后关系不清、专业课程划分不合理等，导致课程设置盲目、课程之间不衔接、课程设置定位不当，从而影响了专业建设及人才培养目标.在高职面临越来越大的社会及校际间竞争压力的今天，这必将对学院的发展和建设带来不利影响.因此，对高职专业课程进行设置，必须充分利用现有的信息进行持续的探索，以构建先进的课程体系、完善的课程设置［2］.笔者基于某学院现有的成绩数据库，在传统关联数据挖掘中引入兴趣度概念并以此为约束条件，利用关联规则数据挖掘和兴趣度阀值挖掘课程间的相关性，深入分析课程设置，为学校的课程总体设置提供参考.

1 相关概念

1.1 关联规则概念

关联规则模型是由R.A Grawal等人提出的基于频繁集理论的数据挖掘方法.此后人们对这一的数据挖掘方式进行了大量研究，提出许多不同的改进算法，使之成为数据挖掘研究中一个相当活跃的领域［2］.其概念如下：

定义1（关联规则）［3］设有项目集I＝｛i1，i2，i3，…，im｝（任意ix≠iy，x，y 为任意不相等的自然数），D为一个给定的事务数据库，D中每个具有唯一的标识符TID的事务T都是I中的一组项目的组合（即T⊂I），则关联规则可以描述为蕴含式R：X⇒Y，其中X⊂I，Y⊂I，X∩Y＝Ø，表示X在某一事务出现，Y也必然会在同一事务中出现.

此规则成立的条件是：

（2）式表示D中包含X的事务中有Confidence的也包含Y.

关联规则挖掘要解决的问题就是在事务库D中发现满足不小于给定的最小支持度和最小置信度阀值的强关联规则.

1.2 兴趣度概念

1.2.1 兴趣度研究的意义 传统关联规则挖掘算法主要考虑支持度和置信度指标，但没有提供好的能够评价规则是否有价值的方法，导致有时满足大于最小支持度和置信度的强关联规则却没有实际意义，甚至有的还具有一定的诱导欺骗性，而且基于这一框架的数据挖掘还有另外的缺陷，就是当二者阀值设得过低时，可能会挖掘出一些矛盾的关联规则，若设得过高，又可能疏漏掉有价值的规则.［4］为此，人们定义了“兴趣度”度量值，弥补传统支持度 －置信度模型的缺陷，充分利用用户的专业知识和经验来对产生的规则进行筛选，避免生成 “干扰性”关联规则影响数据挖掘的结果.

1.2.2 兴趣度的定义 关于兴趣度，许多学者给出不同的定义.文献［5］提出基于模板概念的兴趣度，文献［6］给出概率相关性的兴趣度模型，文献［7］叙述了信息量的兴趣度函数，文献［8］用相关支持度作为衡量兴趣度的方法，文献［9］给出基于兴趣度的正负关联规则的修订.笔者结合研究的需要，引入基于概率统计和Bernoulli实验的兴趣度的定义模式［10］.

定义2（兴趣度） 设定事务数据库D，D上关联规则X⇒Y的兴趣度可表示为

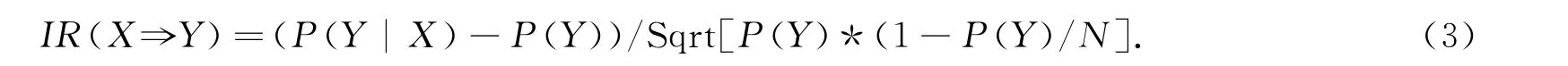
其中：P（Y）表示Y发生概率；P（X｜Y）为X发生的条件下Y发生的概率；Sqrt表示开平方运算；N 为针对事务进行的Bernoulli实验的次数，兴趣值越大，说明规则越有趣，实用价值越高，且对事务X和Y同时都不发生是不敏感的.

例如针对表1数据，P（X）＝208／534≈0.39，P（Y）＝293／534≈0.549，P（Y｜X）＝168／223＝0.753，带入（3）式可得规则（X⇒Y）的兴趣度值：

表1 事务X与事务Y的Bernoulli实验

2 基于兴趣度的关联规则算法

2.1 关联规则基本算法分析

APRIOR算法和FP＿Growth算法是关联规则挖掘2大著名的传统算法，前者是由R.Agrawal和R.Srikant设计的基于频繁项集性质的一种宽度优先先验知识算法，后者是由Jiawei Han等提出的基于频繁模式树的数据挖掘算法.文中重点研究FP＿Growth算法，并在此基础上引入其改进算法.

FP＿growth算法采用分治策略，将频繁项集的数据库压缩成一棵FP频繁模式树，并仍保留项目集关联信息，随后将其分成一组条件数据库，每个关联1个频繁项，而后分别挖掘每一条件数据库.该算法的过程分为2步：第1步构造FP树；第2步是基于FP树挖掘频繁项集.

FP ＿growth算法如下［8］：

输入：事务数据库D；最小支持数阀值Min＿Sup.

输出：频繁模式集.

第1步：构造FP树.

（ⅰ）首次扫描数据库D，得到频繁项集F及支持度计数值i，按i降序排列项集，生成频繁项表L；

（ⅱ）创建以“NULL”为根节点标记的FP树.

针对D中的每个事务做如下操作：对事务中的频繁项按L排序得频繁列表［g｜G］，g为首元素，G为暂未排入的元素列表.当G≠Ø，递归Insert（［g｜G］，T）.

第2步：挖掘FP树的过程.

算法中Insert（［g｜G］，T）函数执行操作是：若G 有子女项M，且M.itemname＝＝G.itemname，则M 的计数值加1；否则新建一节点M，其计数置初始为1，将M 链接到父结点T下，并通过节点链连接到具有相同itemname的节点.

2.2 基于兴趣度的关联规则算法分析与设计

IR＿Growth算法过程与FP＿Growth算法类似，也通过执行以下2步完成：第1步构造频繁FP树，这一步与FP＿Growth算法相同；第2步是利用改进算法对FP树挖掘频繁项集.

下面给出第2步算法过程：挖掘FP树，生成高兴趣度频繁模式.

输入：事务数据库D；最小支持数阀值Min＿Sup；最小置信度阀值Min＿Con；最小兴趣度阀值Min＿Int.

输出：高兴趣频繁模式集.

函数IR＿Rule（ζ）的功能是求出模式ζ所对应的高兴趣度关联规则集，其过程如下：

通过上面的分析可知，IR＿Growth算法中在置信度的基础上引入对关联规则度量一个的新的阀值——兴趣度，根据这个阈值可以将FP＿Growth算法产生的一些不被感兴趣的关联规则删除，从而产生真有趣的关联规则集合，避免一些具有无意义的 “干扰性”关联规则的产生.

3 IR＿Growth算法在高职课程相关性中的应用

3.1 数据准备与预处理

以某高职235名软件技术专业学生主要专业课成绩数据库D为例，部分数据如表2所示.该成绩数据库的能较大程度反映学生的专业学习情况.如果每个学生学号属性可作为事务标识符TID，那么成绩记录可视为事务，而该数据库就是一个事务数据库.由于具体分数表示学生成绩过于细微，不利于挖掘处理，因此采用以下方法对数据进行概化处理：课程名以字母表示；100分制下，75分（含75分）以上者成绩评定等级为“优”，以“1”表示；成绩为75分以下以“0”表示.转化后的成绩数据库如表3所示.

表2 学生成绩事务数据库

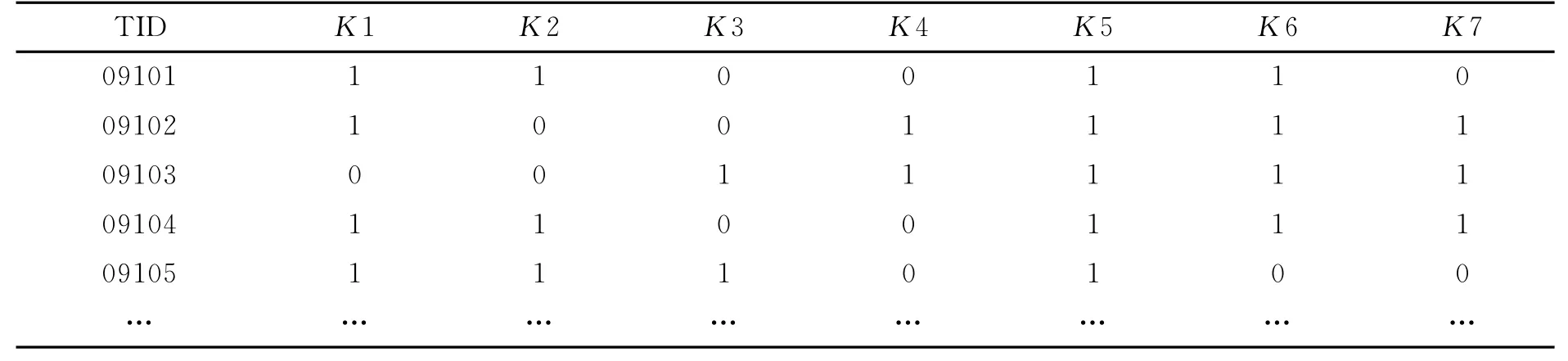
表3 处理后的学生成绩事务数据库

3.2 课程相关性挖掘实现过程

现在所要解决的问题是针对上述类型事务数据库生成支持度、置信度和兴趣度都大于等于最小支持度计数、置信度和兴趣度阀值的关联规则集合，分析某门课程成绩为“优”时对其他课程成绩的影响，以发现课程间的相关性，同时验证IR＿Growth算法的有效性和可用性.

设 Min＿Sup＝10，Min＿con＝60%，Min＿Int＝8，挖掘步骤如下：

（1）生成事务的FP树.

首次扫描成绩事务数据库D，生成频繁项1－项集及相应的支持度，并按支持度降序排列成频繁项表L，L的结构如图1左边所示，项的支持数即为表2中该项列值的累加值.调用Insert（［g｜G］，T）函数过程，创建以“NULL”为根节点标记的FP树，其结构如图1右边所示.

（2）执行IR＿Growth算法过程，挖掘高兴趣度的频繁模式项集.

首先从频繁项表底部项K9→1的节点链的开始，在FP树中，K9的分支路径如表3所示.

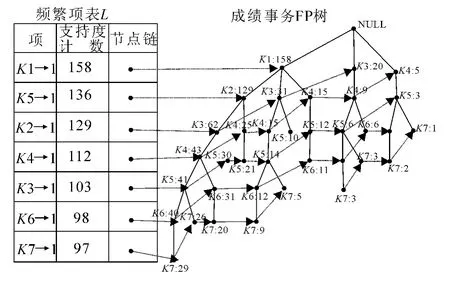
图1 所有成绩事务构成的FP树

表3 含K9的FP树分支及其支持度计数

支持度计数大等于20的只有 ＜K1，K2，K3，K4，K5，K6，K7＞，＜K1，K2，K3，K4，K5，K7＞ 和＜K1，K2，K3，K4，K6，K7＞，此处利用 （2）和（3）式在这2条分支路径中分别计算K6⇒K7和K5⇒K7的置信度和兴趣度：

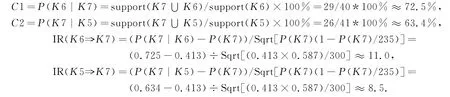
显然，规则K6⇒K7满足大于Min＿Sup＝10，Min＿con＝60%，Min＿Int＝10的要求，将它们加入到含有K7的强关联规则集合.

接着分析含有K6的FP树分支（不再考虑K7），得出K5⇒K6和K4⇒K6满足条件的规则，并加入到强关联规则集合.

依次类推，即可挖掘出所有高兴趣度关联规则组成的集合.

3.3 课程关联挖掘结果分析

用于分析实验的计算机环境为Core i3CPU，2GB内存硬件平台，WindowsXP和SQL Server2005软件平台，以C＃编程环境实现算法.将学生成绩事务数据库挖掘结果集合中的课程代码还原课程名称后，结果如表4所示.

表4 强关联规则集合

从表4可以看出，“C程序设计”应在其他专业课之前开设，为后续课程打下基础；“数据结构”的成绩优秀与否对“数据库及应用”和“JAVA程序设计”成绩有很大的影响，因此要加强“数据结构”的教学，这不仅可以提高后续课程的教学效果，还应在除“C程序设计”外其他的专业课程之前开设.综合对表4的分析，不难得出某学院软件技术主要专业课合理的开课顺序应为：C程序设计→〈数据结构、数据库及应用〉→〈面向对象程序设计（JAVA）、网页制作基础〉→动态网页设计→软件工程.这样的课程设置顺序，既可以保证学生课程学习的连贯性，同时也验证了IR＿Growth算法有一定的实用性.

［1］刘 宁.对高职院校课程建设的反思与重构 ［J］.教育与职业，2011（11）：122－124.

［2］崔学文.关联规则挖掘算法 Apriori在学生成绩分析中的应用 ［J］.河北北方学院学报：自科版，2011，27（1）：44－47.

［3］朱 明.数据挖掘 ［M］.第2版.合肥：中国科学技术大学出版社，2008：156－192.

［4］丁 一，付 弦.基于兴趣度的关联规则挖掘研究 ［J］.情报科学，2011，29（6）：939－942.

［5］KLEMETTINEN M，MANNILA H，RONKAINEN P P，et al.Finding Interesting Rules from Large Sets of Discovered Association Rules［C］／／Proc.of the Third Int’l Conference on Information and Knowledge Management.New York：ACM，1994：401－407.

［6］TANSEL A U，AYAN N F.Discovery of Association Rules in Temporal Databases［C］／／Proceedings of the International Conference on Information Technology.［S.l.］：Institute of Electrical and Electronics Engineers Computer Society，2007：371－376.

［7］SYMTH P，GOODMAN R M.An Information Theoretic Approach to Rule Induction from Database［J］.IEEE Transaction on Knowledge Data Engineering，1992，4（4）：301－316.

［8］徐 勇，周森鑫.一种改进的关联规则挖掘方法研究 ［J］.计算机技术与发展，2006，16（3）：77－79.

［9］高永惠.数据挖掘中关联规则集的优化 ［J］.吉首大学学报：自然科学版，2010，31（2）：38－42.

［10］李永立，吴 冲，王鼠声.一种新的关联规则兴趣度度量方法 ［J］.情报学报，2011，30（5）：503－507.

（责任编辑 向阳洁）

Association Rule Mining Based on the Interestingness About Vocational College Courses

DONG Hui
（Bozhou Vocational and Technical College，Bozhou 236800，Anhui China）

Absract：This paper studies the association rules data mining，the concept of interestingness and algorithm design based on the concept.Taking vocational college’s achievement database for processing object，this paper analyzes the association rules of courses；and with interestingness as constraint conditions，deceptive invalid association rules are eliminated，and some reliable interesting association rules of courses are discovered.This paper provides reference for vocational college curriculum design and syllabus revision，and it also verifies the validity of the algorithm.

data mining；association rules；interestingness；course－setting

TP311

A

10.3969／j.issn.1007－2985.2012.03.011

1007－2985（2012）03－0041－06

2012－04－17

亳州职业技术学院自然科研基金资助项目（BYK1105）

董 辉（1975－），男，安徽亳州人，亳州职业技术学院信息工程系讲师，硕士，主要从事数据库、数据挖掘研究.