Rasch模型在等级量表设计中的应用
杨建原 曾薇
Rasch模型在等级量表设计中的应用
杨建原 曾薇
本文以贵州师范大学共90个大一新生在症状自评量表上的数据为实例,讨论Rasch等级模型在设计和修订等级量表中的应用,以及如何应用Rasch等级模型的某些参数如选项频率、平均测量值、临界值、概率曲线、选项拟合指数等来对等级量表的选项分类数目、选项标签进行直观的分析和检验,从而获得高质量量表。实例分析结果显示量表的各项指标均符合Rasch等级模型的规定,数据对模型的拟合非常好。
Rasch等级模型;平均测量值;临界值
1 引言
要分析一份问卷或调查数据的质量,首先要分析问卷中选项的功能。等级量表一般仅调查某个特征,只描述与调查问题相关的因素,这个因素就是“潜在特质”或“变量”。在等级量表中呈现选项的目的就是为了获得被试在某个变量上的清晰定位。但在某些情况下,被试并没有按照量表设计者所期望的那样进行反应[1]。
作答等级量表的过程其实就是量表设计者的意愿与被试的态度、行为在双方均感兴趣的问题上进行的一种交流。创建等级量表的方式会对由该量表所收集的数据的质量产生很大的影响[2],原因是对某个变量的测量来说,如果量表项目采用的选项分类(比如是非题的选项分类就是“同意”和“不同意”)不一样,那最终得到的量表可能因为分类不同而导致其质量不同。因此等级量表不仅要能详细反映设计者思考问题的过程,而且所使用的选项标签(标签就是选项分类的语言表述)要能得到被试清晰的反应。项目的选项标签及数目均会影响量表的质量,如何确定合理而有效的选项呢?Guil⁃ford(1965)认为等级量表中项目的选项应该要界定准确、相互排斥、意义明确、详尽无遗。Rensis Likert(1932)的早期研究表明不具备次序性的差异化选项是无效的,他由此提出了著名的5点(5个选项)同意量表。Nunnally(1967)在总结 Guilford(1954)的研究的基础上报告:“根据心理测量理论,使用选项多的量表比使用选项少的量表一直更具优势”。然而他又说“过多的选项分类会迷惑被试并激怒他们”。Stone和Wright(1994)在一项对恐惧的调查中证明将选项分类数目从5个合并为3个时,测验的信度增加了。Zhu等[3]在对自我效能感的测量中也发现了类似的结果。研究者们对如何确定等级量表的选项没有达成一致意见,所以有必要对等级来量表的选项功能进行研究。恰好Rasch分析[4]能提供一个有效的框架,在该框架内,可以验证、改进等级量表选项的功能。
2 等级量表的Rasch测量模型
Andrich(1978)提出了在顺序等级量表上建构了一个基本的Rasch模型(rating scale model,RSM):
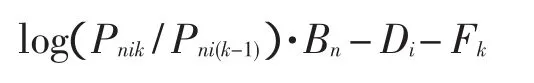
(其中,Pnik是被试n在项目i上选择选项k的概率;Pni(k-1)是选择选项k-1的概率;Bn是被试n的能力或态度等;Di是项目i的难度;Fk是指选项k和选项k-1之间的“距离”或“差异”,选项用0到m进行编码,称Fk为第k个等级标度(step calibration),Fk即是等级量表的临界值,其被界定为是与相邻两个选项k和k-1的选择概率相一致的定位。)Rasch模型是将被试的特质水平和项目的难度都放在同一个量尺(logit量尺)上来进行度量的一种模型,其最大优点就是可以直接对这两个参数(被试的水平和项目的难度)进行比较。相对同类其他模型来说,它最重要的理论特征就是具有“客观性”[5],因为比较两个项目的难度不依赖于被试的能力,同样比较两个被试的能力也不依赖用于测量的项目。在“部分计分(partial credit)”的项目中,该模型可简化为:

但为了方便,在限制条件∑Fik=0,∑Dik=∑Di下:重新令Dik=Di+Fik。RSM只是部分计分Rasch模型(partial credit model,PCM)的一个子集,因为RSM规定所有项目的选项分类之间的等级间距要相同,而PCM没有规定。Rasch等级模型不仅满足从顺序研究中创建线性测量的条件和需要[6],还能为等级量表的施测提供基础。某些Rasch参数(如临界值)还能够反映出等级量表的结构[7]。
3 Rasch模型对项目选项分类的检验
要对量表的质量进行检验,最有效的方法是先对它的选项分类进行检验。以Likert五点量表来说,若量表的5个选项分类为非常反对、反对、不确定、同意、非常同意,则这五个选项分类之间的间距及尺寸大小是一样的,本质含义这些选项同等重要,要求得到被试同样的注意。从测量的角度看,等级量表虽有不同的选项分类设置,但选项分类之间仍形成清晰的等级,并囊括了全部潜在变量,如图1所示。

图1 典型的Likert量表
但变量的概念是无限的,使得两端选项分类的宽度无限。比如一个被试选择了“同意”,就可以假定他的同意程度已经很强烈了,“同意”选项涵盖了更多的潜在变量(“同意”选项的空间尺寸较大)。中间选项的空间尺寸大小取决于被试的理解,将中间选项“不确定”换为“不知道”、“不在乎”、“不肯定”等表述不仅会影响它的心理学意义,还会影响其所囊括的潜在变量的数量,它的尺寸如图2所示。一般来说,被试都有社会遵从的倾向,即多赞同或少冷漠,“同意”选项通常比“反对”更具吸引力。因此“同意”选项倾向于涵盖了潜在变量的更宽范围。实际上,数据不能完全符合Rasch模型的规定。但从解决问题这一目的来看,只要理论结果与实际近似就行,不需要过分精确[8]。

图2 潜在变量
3.1 选项分类的设置
比如要求被试对“老板支持我的工作”这一观点的认同度作出反应,被试做出的选择将取决于量表所提供的反应选项的数量及类型。下面有三个量表选项A,B,C,如图3所示。

图3 三个量表选项
从选项分类上来看,量表选项A被设计成为“是非”题的形式:老板要么支持要么反对我的工作。量表选项B允许被试保持中立,不逼迫其作出极端选择。量表选项C对变量的概念作了更多的界定,将被试所感知到的支持程度描述成连续的,明显优于其他量表。通过设置不同的选项分类来设计等级量表,等于是将量表设计者关于支持的观点传达给被试。但在实际情况中,被试需要更多的选项分类来表述自己的观点吗(正如量表选项C)?如果有更多的选项分类可供选择,被试实际上会用到这么多吗?对于被试来说很完美的选项分类数量和类型是否可以得出完美的测量分析?这些疑问都指向同一个重要的问题:对于最优的变量测量,选项分类的实际数目应是多少?
相当多的研究尝试解决怎样确定等级量表的选项数目这个问题。判断选项分类设置最佳数目的一般标准是信度。但是研究者在信度问题上得出的结论却很混乱:有的学者认为信度和分类选项的数目之间是相互独立的(Bendig,1953;Brown,Widing,&Coulter,1991;Komorita,1963;Reming⁃ton,Tyrer,Newson-Smith,&Cicchetti,1979)[9];另一些学者认为7点量表的信度最高(Finn,1972;Nun⁃nally,1967;Ramsay,1973;Symonds,1924)[9];或者是7点量表加2或减2(Miller,1956);也有的认为是5点量表信度最高(Jenkins&Taber,1977;Lissitz&Green,1975;Remmers&Ewart,1941);还有的认为是4点量表或3点量表信度最高(Bendig,1954)[10]。
下面是一个常见的7点量表,如图4所示。
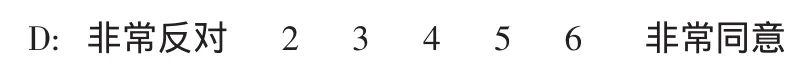
图4 7点量表
使用D的等级量表是否比使用A、C的更加有效?增加更多的选项分类是否有用?研究表明,尽管增加选项分类会使得信度提高,但仅限于选项分类增加不是随意的[11,12]。比如D中,选项分类5与6之间的区别模糊,让被试感到很迷惑,最终使得分数的意义受到影响[13]。正如Chang(1994)所阐述的那样,允许被试在模糊的参照框架中自由选择,增加可供选择的选项分类会增加误差。在此种情形下,就所用量表而言,被试与调查者之间对同一问题的理解可能会不一样。比如,两个被试所感知到的支持程度是一样的,其中一个选择5而另一个选择6,仅仅是因为引入的选项类别过多导致变量的概念混乱了。
对于等级量表来说,实际上并不存在固定的最佳选项分类数目。5个选项分类的量表对某个测量来说有效,而“是”“非”类型的选项设置可能对另外一个测量来说却最适合。因此,当调查者设计不同的量表时,或用同一量表测试其他的被试时,都要重新确定最佳的选项分类数目。因此分析时需根据所欲测量的具体对象来确定等级量表的最佳选项分类数目,而不仅仅就是为了确定而确定[14]。
3.2 确定选项的标签
和选项分类不同,但也选项分类密切相关的是选项分类的标签。看量表选项E和F,如图5所示。
量表选项E比F模糊,因为它的一些选项分类没有标签。F的标签很明确,并且其语言表述积极的,按钮F中包括了三个“同意”选项,但只有两个“反对”选项。
在等级量表中,从量表选项A到F都包括了某种假设:即被试能感知变量概念,并能通过等级量表将这种感知和设计者进行有效交流。对量表的质量进行检验就相当于对这一假设进行检验。Rasch模型能够提供一些参数来对这一假设进行检验。

图5 选项分类的标签
4 对等级量表进行Rasch分析
设计等级量表所面临的核心问题是:从被试和项目上所收集到数据是否可信?选项分类和Rasch模型是否能充分拟合?临界值能否显示出等级量表中的层级?每个选项分类上是否有足够的数据来提供稳定的参数估计?本文以贵州师范大学共90个大一新生在SCL-90上的数据为例子,运用Rasch模型分析软件winsteps对该样本在SCL-90上的有效性进行检验,讨论如何运用Rasch模型来设计和修订等级量表。需要特别说明,本例样本只有90个被试,对于包含90个项目的SCL-90来说显然样本量太小,但这里只是将其作为一个例子介绍Rasch模型在分析等级量表中的使用方法,并非是一项真实研究,应该是可以接受的。
要对等级量表进行Rasch分析,首先要估计量表项目的维度。因为Rasch模型最关键、最基本的假设就是量表项目要具有一维性。可以使用非加权最小二乘法来对收集到的数据做探索性因数分析[15]。如果项目的第一个特征根比第二个特征根大很多,而第二个特征根和其他的特征根相差不大,就可以初步判断量表的项目是一维的[16,17]。本研究中,第一个特征根值26.5,第二个是3.9,其余的特征根与第二个相差不大。因此符合Rasch模型分析的一维性假设。
4.1 Rasch参数:选项频率及平均测量值
评估选项分类的设置是否有效,最简单的方法就是使用统计指标(如选项分类频率、平均测量值)对每个选项分类进行检验[7,11,17,18]。选项分类频率(category frequencies)是指选择某一选项的被试的数量,其值等于在所有的项目上选择某一选项的被试总和。选项频率反映了所有选项分类的反应分布,能对等级量表进行快速的检验。
选项频率有两个主要的特征:选项分布形态和每个选项分类的作答数量。常规分布有一致分布、正态分布、双峰分布、轻微偏态分布,非常规分布包括高偏态的分布(即选择数少的选项其分布形态有着一条长尾巴)[19]。符合常规分布的选项频率分布要优于非常规分布。但在临床症状数据中选项频率呈现偏态分布的比较常见,那些症状明显的病人,一般其位置均位于长长的尾巴上。
频率低的选项一般是有问题的,因为它们没有为估计稳定的临界值(threshold values)提供足够的数据。选项频率很低就意味着它是不必要的或多余选项。因此,这些选项应该合并或压缩到相邻的选项上。如果在某一选项上反应的数量少于10,这个选项就需要修订[19]。
平均测量值(average measure)能直观有效地检验等级量表的选项。其定义为选择某特定分类选项的所有被试的平均能力估计,其值是选择某特定选项类别的所有被试的平均能力估计值[11],如表1所示。

表1 90个被试的SCL-90的选项频率及平均测量值
当变量增加时,平均测量值也会随之增加。Rasch模型规定选项的平均测量值要呈单调递增。意思是那些有着高能力或态度强烈的被试会选择更高的作答选项,而低能力或态度不强烈的被试会选择较低的作答选项。当违背了这种形式,就表示平均测量值没有显示出单调性,可能就需要对作答选项的分类进行合并。表1是SCL-90量表的Rasch分析结果,它有5个选项分类,4个等级。例子中的选项分类频率(如选择数量)呈现正偏态的分布,每个选项分类上的选择数均大于10个,符合Rasch模型的规定。选项分类1的平均测量值是-2.80,意思就是在SCL-90量表中,选择选项分类1的被试其症状平均符合度的估计值是-2.80或其logit分数是-2.08。选择选项分类2的被试,其平均的症状严重程度的估计值是-1.00,表明选择选项分类2的这些被试他们的症状严重度要比选择1的高。从表1中可以看到,平均测量值符合Rasch模型的规定,因为它们都呈单调递增。
4.2 Rasch参数:临界值和选项拟合
除了选项类别频率和平均测量值之外,其他描述等级量表特征的指标还有临界值(thresholds)和选项分类拟合值(category fit)。临界值(也称等级刻度,step calibration)最难估计,原因是很难真正区分一个选项和另外一个选项之间的区别,例如很难评估“非常同意”和“同意”之间的真正区别。与平均测量值一样,临界值也要呈单调递增。如果等级量表的临界值不呈单调递增,那么可认为这个量表的等级是混乱的。
估计相邻两个临界值之间的距离的大小也很重要,临界值之间的距离指的是变量的每个等级在量尺上的不同位置。在logit量尺上,这个距离不能太小也不能太大。一般来说,临界值至少要以1.4 logit的量增加,才能显示出两个选项类别之间的差异,但增量不要超过5 logit,避免变量等级之间的间距过大[19]。
要研究临界值之间的差异,最直观的一种方法就是看概率曲线(probability curves)。概率曲线能显示等级量表中被试选择各个选项分类的概率。在概率曲线图中,每一选项分类都有一个明显的波峰,这个波峰表明在所测量变量的某部分上,这一选项分类是最可能被选择。若图中的某个选项分类的形状是平直的,并且涵盖了变量的大部分,这种情况还是可行的,但是若这些呈平直形状的选项分类被其他选项分类的概率曲线图遮住,那它们可能对界定变量的区别作用不大。因此,选项间的临界值有问题,其概率曲线图就比较混乱或靠得较近,在变量上只有一小段跨度很小的平直曲线,如图6所示。
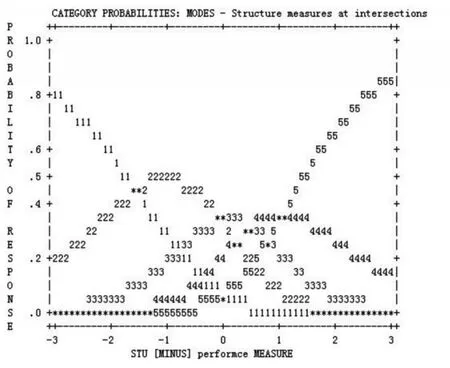
图6 SCL-90的5个选项分类的概率曲线
图6是SCL-90所有选项分类的反应概率图,它给出了任意被试的能力与项目难度之间的差异估计。例如,一个被试的水平是1 logit,比项目的难度低,位于x轴上-1的位置,他选择选项分类1的概率几乎为0,选择分类4的概率大约为0.03,选择分类1和3的概率大约为0.2,选择分类2的概率大约为0.5。所以该被试在这个项目上最可能选择选项分类2。如果被试的水平高于某给定项目的难度,如在x轴上+2的位置,那他最可能选择的选项应该是5,如表2所示。
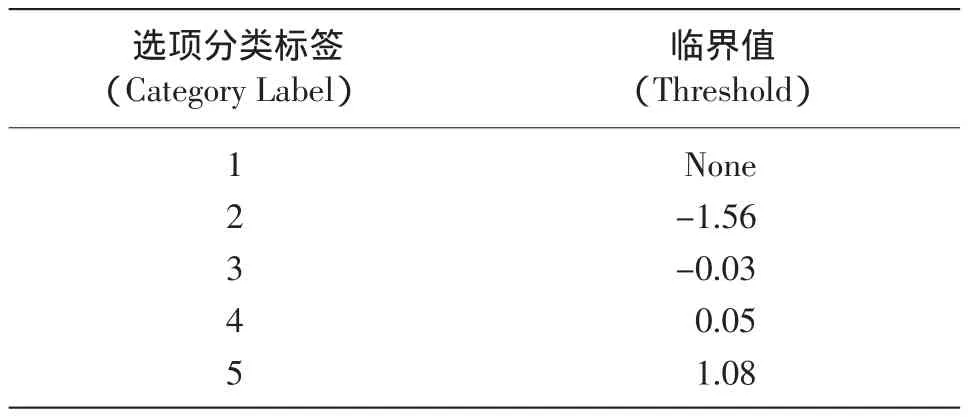
表2 90个被试的SCL-90的选项临界值
表2是对SCL-90的临界值的估计,它与图1中选项分类的交叉点是一致的。每个临界值表示了所测量变量的相邻两个选项分类之间的等级差异。例如,表2中的第一个临界值是-1.56,找到图1中选项分类1与2的交点,通过这一交点作x轴的垂线,垂线与x轴的交点在-1.56处。从表2中可以看出。除第一个和第二个临界值之间其增量大于1.4 logit之外,其余各分类的临界值之间的差异都小于1.4 logit,这里的分析结果表明SCL-90的选项分类3、4和5之间的等级差异不是特别明确清晰,差异大小也不是等距的。这有可能是被试太少,或都是大一新生,比较同质。但这个结果比较符合现实意义,因为在现实情况中,对于SCL-90量表的选项分类,“无”与“轻度”之间的距离和“中度”与“偏重”之间的距离,这两个距离是不等同的。
不拟合均方值(outfit mean squares)是选项拟合值之一,它是评估等级量表质量的另外一个标准,不拟合均方值大于2表明没测量到的变量信息比测量到的多(Linacre,1999),也就是某些选项分类将噪音引入了测量过程。在下一步的实证调查中,可能要将这样的选项分类压缩到邻近的选项中。表3显示了SCL-90的每个分类选项与线性Rasch模型的拟合情况。所有项目的不拟合均方指数均小于2,均符合Rasch模型的规定。
5 总结
本文以SCL-90的测量数据为例子,展示了Rasch模型分析在等级量表中的用法及功能。因为Rasch模型是一个先验模型,它的一个重要的特点就是数据要拟合模型,而不是让模型去拟合数据。前面讨论的有关等级量表诊断指标包括选项频率、平均测量值、临界值、概率曲线和选项分类拟合,在用这些指标去检验量表质量的时候,应当将它们联合起来运用。其实,它们都是从不同侧面来检验同一个问题。例如:如果某一选项分类的频率太低,那临界值的排序是混乱的,等级量表上每个选项分类的概率分布曲线也没有明显的波峰。同样地,平均测量值的排序也是混乱,并且拟合统计指标比预期的大。并不是每种情况下所有的指标都出现上述的情况。但当联合使用这些诊断指标时,可以有效指出等级量表中需要修改的地方,以提高等级量表的信度和效度。
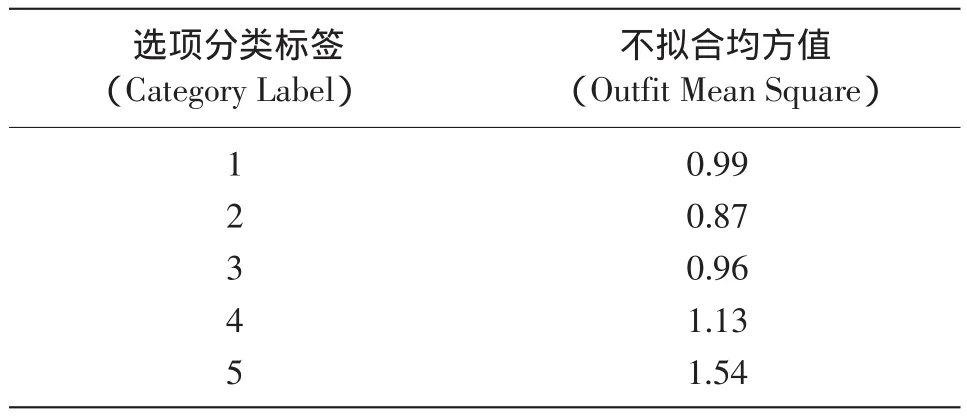
表3 90个被试的SCL-90的选项分类拟合
[1]Roberts,J.,Rating scale functioning,in Rasch Measurement Trans⁃actions.1994.p.386.
[2]Clark,H.H.and M.F.Schober,Asking questions and influencing answers.Questions about questions,1992:p.15-48.
[3]Zhu,W.U.W.F.,Post-Hoc Rasch analysis of optimal categorization of an ordered response scale,in Journal of Outcome Measurement.1997.p.286-304.
[4]Rasch,G.,On General Laws and the Meaning of Measurement in Psychology,in Paper at the Fourth Berkeley Symposium on Mathe⁃matical Statistics and Probability,Statistical Laboratory,Universi⁃ty of California,June 20-July 30,1960.
[5]Rasch,G.On Specific Objectivity:an Attempt at Formalizing the Request for Generality and Validity of Scientific Statements,1977,Danish Yearbook of Philosophy,14,58-93.
[6]Jr.William P.Fisher,On Rasch Measurement,HSR Reports Pro⁃file.1995.
[7]Andrich,D.A.,A rating formulation for ordered response catego⁃ries.,in Psychometrika.1978.p.561-573.
[8]Laudan,L.,ed.Progress and Its Problems:Towards a Theory of Sci⁃entific Growth.Berkeley,CA:University of California Press.1977.
[9]Trevor G.Bond,C.F.,Applying the Rasch Model:Fundamental Measurement in the Human Sciences.,in Lawrence Erlbaum Asso⁃ciates.2007.p.159.
[10]Linacre,J.M.,Categorical misfit statistics.1995.
[11]Linacre,J.M.,Categorical misfit statistics.Rasch Measurement Transactions,9(3),450-451.,in Available from http://www.rasch.org/rmt/rmt93.htm.Accessed March 15,2000.1995.
[12]Wright,B.D.L.J.,Combining and splitting of categories.Rasch Measurement Transactions,6(3),233.Available from http://rasch.org/rmt/rmt63.htm.Accessed March 20,200.1992.
[13]Fox,C.G.J.D.,The use of Rasch analysis to establish the reliability and validity of a paper-and-pencil simulation.,in Paper presented at the annual meeting of the Midwestern Educational Research As⁃sociation,Chicago.1994.
[14]Lopez,W.,Communication validity and rating scales,in Rasch Measurement Transactions.1996.p.482.
[15]Muth E N,L.K.and B.O.Muth E N,Mplus.Statistical analyses with latent variables.User’s guide,1998.3.
[16]Traub,R.E.and R.K.Hambleton,Note of correction on the article entitled"The effect of scoring instructions and degree of speeded⁃ness on the validity and reliability of multiple-choice tests.".Edu⁃cational and Psychological Measurement,1973.
[17]Lord,F.M.,Application of Item Response Theory to Performance.,in Journal of Outcome Measurement,1(2),143-163.1980.
[18]Andrich,D.A.,Measurement Criteria for Choosing among Models with Graded Responses,in Analysis of categorical variables in de⁃velopmental research.Orlando FL.1996,Academic Press:San Di⁃ego.p.3-35.
[19]Linacre,J.M.,Investigating rating scale category utility.J Outcome Meas,1999.3(2):p.103-22.
Applied Rasch Modeling in Rating Scale Design
YANG Jianyuan and ZENG Wei
In this article SCL-90(Chinese version)was used to illustrate how to use Rasch model to analyze rating scale.In the Rasch analysis,a useful method to obtain diagnostics in evaluating category usage is to examine the average measures and threshold of each category,probability curves of each item and the item fit mean squares(MNSQ).The number and the lables of categories of response choices were empirically analyzed and the results indicated that SCL-90 satisfied most important theoretical merits of Rasch model including the two MNSQ statistics widely used infit(weighted)and outfit(unweighted).
Rash Graded Model;Average Measure;Threshold
G405
A
1005-8427(2012)05-0012-7
本研究为贵州省高等学校教学质量与教学改革工程重点项目“基于PBL理论改进心理教育测量教学改革研究”(项目批准号:黔高教发[2011]28-1)、贵州师范大学精品课程“心理测量”建设项目阶段性成果。
贵州师范大学

