地震作用下相邻结构的防震缝宽度确定方法

卢明奇，杨庆山

(北京交通大学土木建筑工程学院，北京 100044)

地震作用下相邻结构的防震缝宽度确定方法

卢明奇，杨庆山

(北京交通大学土木建筑工程学院，北京 100044)

目前中国现行抗震设计规范中所规定的防震缝宽度取值一般较小，且缺乏理论依据，不能有效防止地震作用下相邻建筑之间发生碰撞，为此对相邻结构在地震作用下的最大相对位移进行研究。分别讨论周期比、高度比等因素的影响作用，在此基础上给出两单自由度体系最大相对位移的计算方法，并进而确定相邻结构的防震缝宽度。结果表明:任意高度比的相邻单自由度体系最大相对位移可由高度比为1和0两种情况求得;所提出的防震缝宽度确定方法的计算结果与时程分析结果较为接近，说明所提方法较为准确，可以用于相邻结构防震缝宽度的设计。

防震缝;相邻结构;周期比;高度比;最大相对位移;碰撞

以往震害调查表明，相邻结构在地震过程中的碰撞是导致结构损坏甚至倒塌的主要原因之一［1-6］。《建筑抗震设计规范》(GB 5001l-2010)［7］对钢筋混凝土结构给出了最小防震缝宽度要求，但规范给出的防震缝间距并没有充分考虑相邻结构自振特性的影响，所给出的防震缝的宽度也主要为经验取值，缺乏理论依据。文献［8］～［13］中分别对相邻结构地震碰撞和防震缝间距进行了研究，但是并未给出合理的防震缝宽度计算方法。为此，笔者对相邻结构在地震作用下最大相对位移进行研究，提出防震缝宽度设计计算方法。

1 相邻单自由度体系的最大相对位移

当两相邻结构在地震过程中的最大相对位移小于防震缝的宽度时，可以保证二者之间不发生碰撞，即需满足如下条件:

式中，D为相邻建筑间预留的防震缝宽度;Δxmax为地震作用下两相邻结构的最大相对位移。

首先对两相邻单自由度(SDOF)体系的地震最大相对位移进行研究。设如图1(a)所示具有相同高度的两单自由度体系，在地震作用下分别建立两单自由度体系的运动微分方程

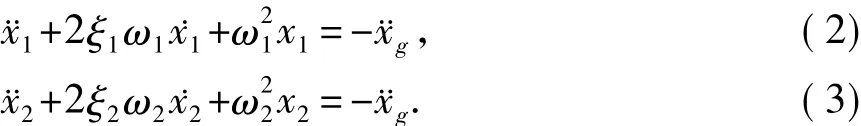
式中，ξ1、ω1、T1、x1、˙x1、¨x1分别为体系1的阻尼比、圆频率、周期及相对于地面的位移、速度、加速度; ξ2、ω2、T2、x2、˙x2、¨x2分别为体系2的阻尼比、圆频率、周期及相对于地面的位移、速度、加速度。体系2相对于体系1的位移Δx=x2－x1，相对速度Δ˙x=˙x2－˙x1，相对加速度Δ¨x=¨x2－¨x1，将式(3)减去式(2)，得

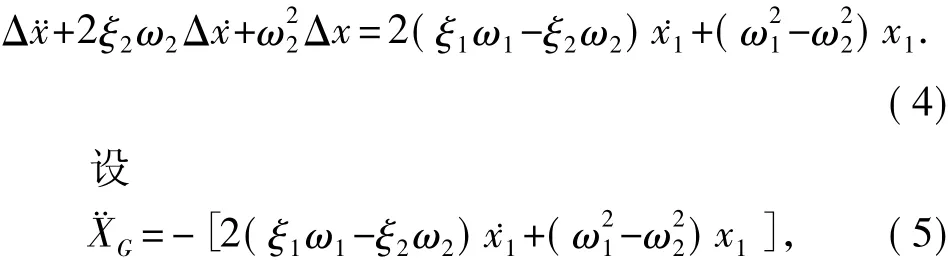
则式(4)可表示为

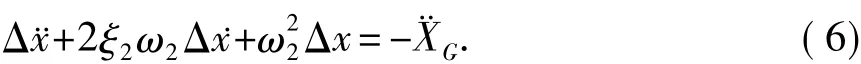
联立求解式(2)、式(6)即可求得相对位移Δx的时程曲线。

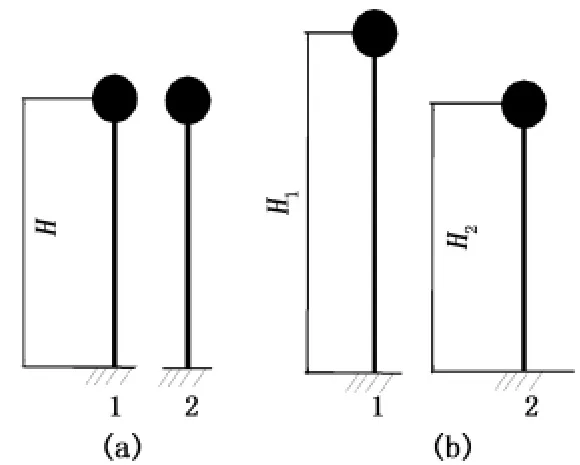
图1 两单自由度体系Fig.1 Two SDOF systems

若两个单自由度体系具有不同高度(图1 (b))，设体系1的高度H1大于体系2的高度H2，定义高度比

设体系1在高度H2处的位移为αx1，相对位移Δx=x2－αx1。将式(2)－α×式(1)，化简得

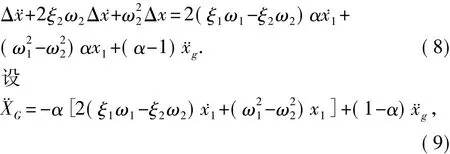
则式(8)也可写成式(6)的形式。联立求解式(2)、式(6)同样可计算出不等高体系相对位移Δx的时程曲线。对Δx取最大值，即可得到两单自由度体系的最大相对位移Δxmax。

从美国PEER地震记录数据库中选择100条实际地震记录计算不同周期比下相邻单自由度体系最大相对位移，将地震波加速度峰值统一调整为0.3g。设T1=0.5 s，研究高度比α对最大相对位移Δxmax的影响作用。取T2=0.1，0.2，…，3 s，阻尼比ζ1=ζ2=0.05，分别计算α=0，0.2，0.5，0.8，1的情况下Δxmax。其中，α=0意味着体系2的高度为0，这对于实际工程结构而言是不现实的，本文中对其进行计算主要是为了从理论上确定高度比α较小时的极限状态。图2为按上述100条地震记录计算得到的地震最大相对位移Δxmax平均值与周期比T2/ T1关系曲线，其中横轴采用对数坐标表示。

由图2可见，α=1时(即两等高单自由度体系)，在T2/T1=1处Δxmax等于零，这是因为如果两等高单自由度体系具有相同的振动周期，在振动过程中二者均保持同步运动，所以相对位移恒为零。当T2/T1＜1时，Δxmax随着T2/T1减小而增大;T2/T1＞1时，Δxmax随着T2/T1增大而呈增大趋势。当α=0时，随着周期比T2/T1增大，Δxmax亦呈增大趋势。当α=0.2，0.5，0.8时，最大相对位移Δxmax与周期比T2/T1的关系曲线介于α=1和α=0两者之间，当α接近于0时，曲线形式接近于α=0的情况;反之当α接近于1时，则曲线形式接近于α=1的情况。

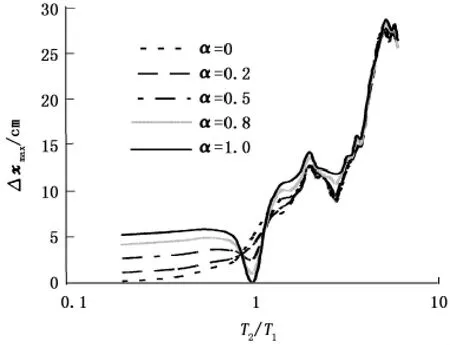
图2 两相邻单自由度体系最大相对位移平均值与周期比的关系曲线Fig.2 Relation between period ratio and average values of maximum relative displacement of two adjacent SDOF systems

最大相对位移Δxmax可表示为周期比T2/T1和高度比α的函数，即可表示为Δxmax(α，T2/T1)。通过计算发现

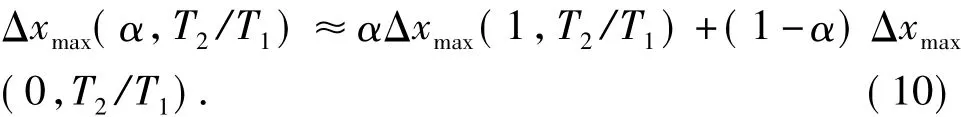
图3中给出了α=0.2，0.5，0.8时按实际地震记录计算得到的Δxmax平均值与T2/T1关系曲线和按照公式(10)计算得到的Δxmax与T2/T1关系曲线，可见二者吻合较好。当α等于其他值时，可得到相同的结论。

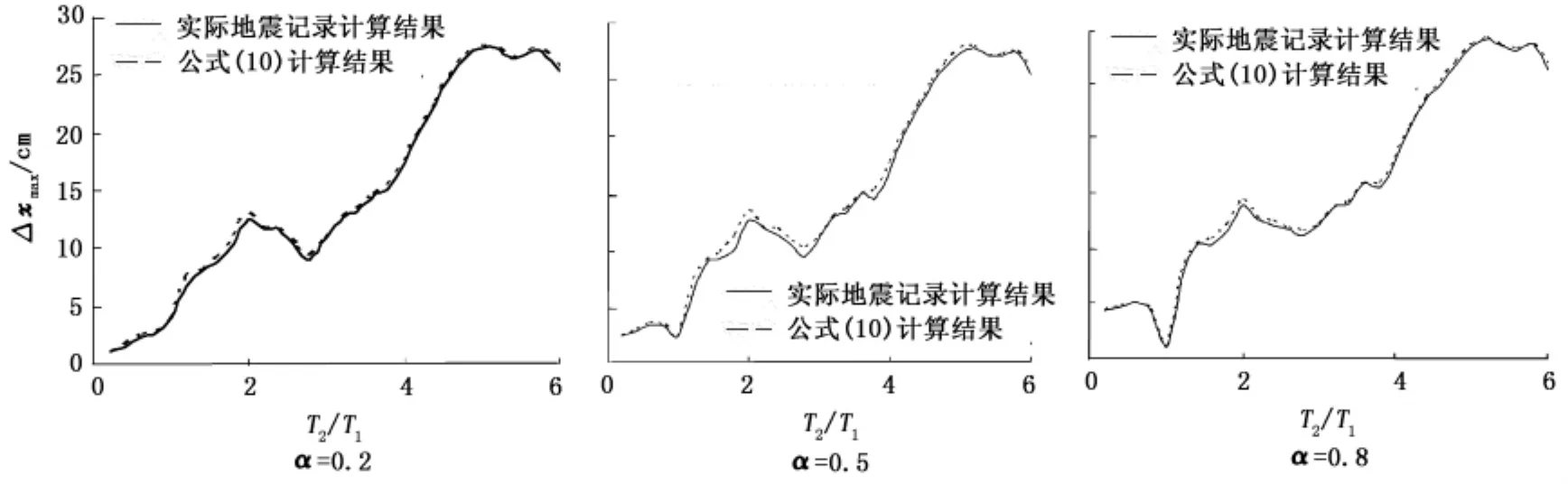
图3 不同高度比下最大相对位移曲线与公式(10)计算结果对比Fig.3 Comparison between maximum relative displacement with different height ratios and calculation results by formula(10)

2 单自由度体系最大相对位移

2.1 α=1时的最大相对位移

α=1代表着两个相邻单自由度体系等高。Kasai等［10］提出了SPD计算方法可用于计算两等高单自由度体系的最大相对位移Δxmax(α=1)，其计算公式为

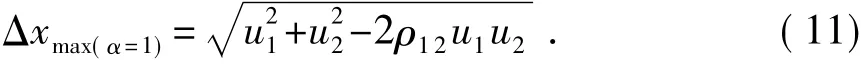
其中，u1、u2分别为两结构的最大位移反应，可以通过地震位移谱求得。设两个单自由度体系阻尼比相等，则ρ12可表示为

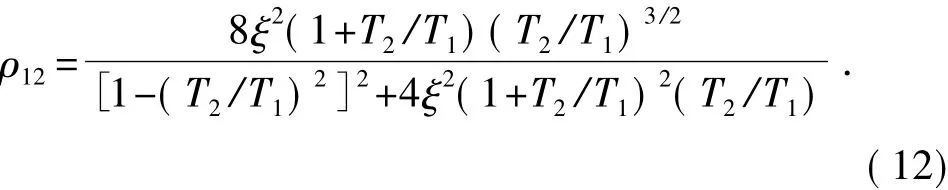
2.2 α=0时的最大相对位移

当α=0时，由式(8)等号右边等于－¨xg，则式(8)变为

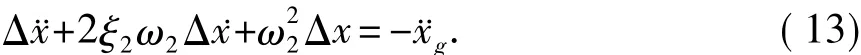
对比式(13)和式(3)，可见二者具有相同的方程形式，所以两个方程中的Δx与x2势必同解。高度比α=0时，Δxmax(α=0)等于体系2的最大位移反应u2，u2可以通过地震位移谱求得。

2.3 0＜α＜1时的最大相对位移

要确定0＜α＜1的两单自由度体系最大相对位移，可首先确定α=1和α=0时的最大相对位移，然后由式(10)计算其最大相对位移。

需要注意的是，上述方法虽然是针对两单自由度体系提出的，但是对于以第一阶振型为主导振型的大多数多层结构而言，可以将其等效为单自由度体系，仍可按照上述方法计算其地震最大相对位移。对于高层建筑，原则上不能简单地等效为单自由度体系。但是在实际震害中，高层建筑与高层建筑之间往往间距较大，一般不会发生彼此碰撞，常见的是高层建筑与其裙房由于防震缝宽度不足而发生的相互碰撞。这种情况下，裙房一般相对较矮，并为多层建筑，此时裙房可等效为单自由度体系;对于与裙房相邻的高层建筑，由于高阶振型主要影响结构的上部位移，对于结构底部位移的影响较小，可以忽略，所以也可近似等效为单自由度体系。

3 相邻结构的防震缝宽度

对于两相邻结构，若可将其等效为两单自由度体系，其最大相对位移

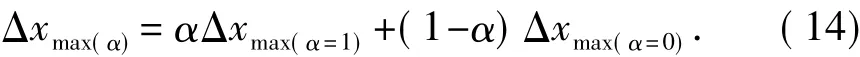
根据公式(1)，防震缝宽度不小于Δxmax(α)才能保证结构在地震作用下不发生碰撞，即

4 算例分析

分别采用时程分析方法和本文中所提出的方法对两相邻多层建筑、高层建筑与相邻裙房两种情况的地震最大相对位移进行对比分析。

4.1 两相邻多层建筑的防震缝宽度

设两相邻钢筋混凝土多层框架结构，结构1为两跨三层，建筑高度H1=12.8 m，结构2为1跨两层，建筑高度H2=7 m。框架梁、柱截面形式如图4所示。对这两个结构进行模态分析，得到结构1的基本自振周期T1=0.247 s，结构2基本自振周期T2=0.173 s，阻尼比均为5%。可得，两结构周期比T2/T1=0.7，高度比α=0.547。

选取上述100条实际地震记录(地震波加速度峰值统一调整为0.3g)对两框架进行时程分析，计算在结构2(相对较矮的建筑)顶层高度处的两结构地震最大相对位移。各地震记录计算得到的地震最大相对位移取平均值为3.63 cm。按照本文方法得到的地震最大相对位移为3.74 cm，二者误差为3%，说明本文方法较为准确。所设计的防震缝宽度大于3.74 cm能满足工程抗震中的防撞要求。

图4 两相邻多层结构Fig.4 Two adjacent multi-stories structures

4.2 高层建筑与相邻裙房间的防震缝宽度

设一幢两跨11层的高层钢筋混凝土框架结构，建筑高度H1=38.5 m，其裙房为两跨三层的钢筋混凝土框架结构，建筑高度H2=12.8 m。框架梁、柱截面形式如图5所示。

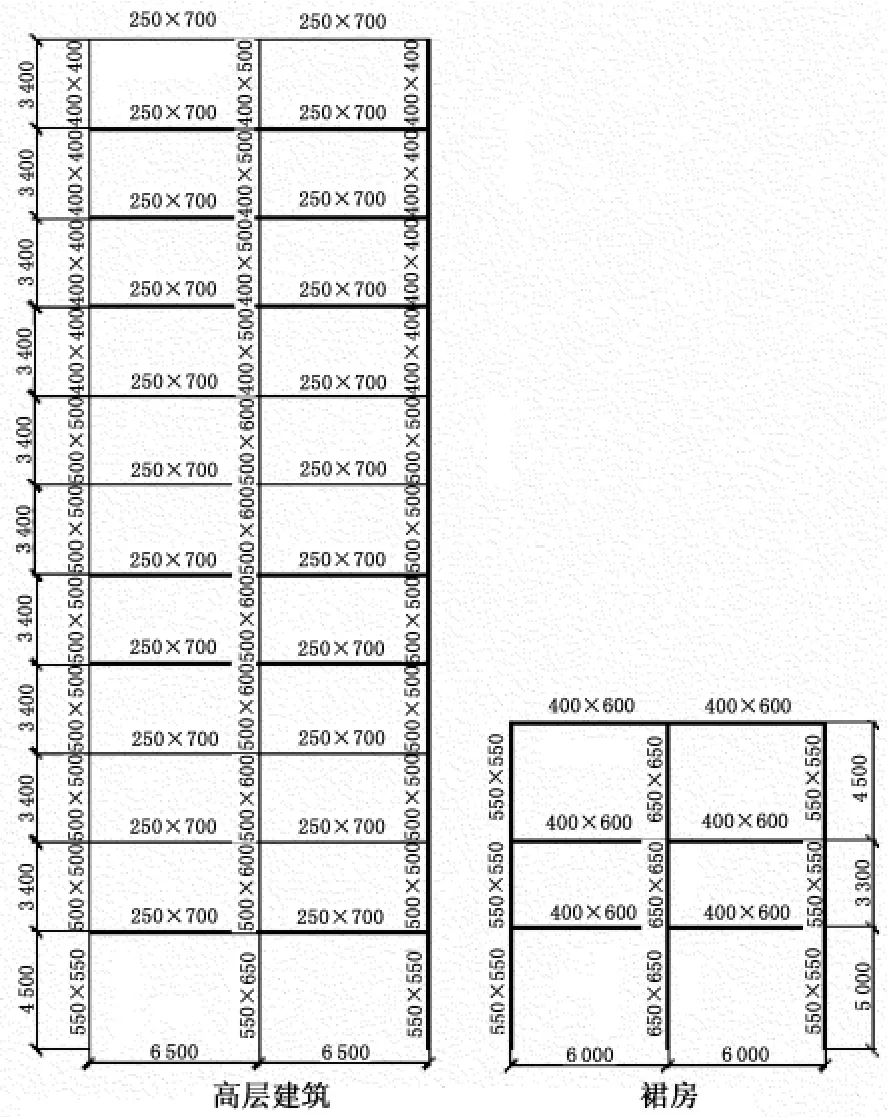
图5 高层建筑与裙房Fig.5 High-rise building and its annex

对这两个结构进行模态分析，得到高层建筑的基本自振周期T1=0.705 s，裙房的基本自振周期T2=0.247 s，阻尼比均为5%。可得，两结构周期比T2/T1=0.35，高度比α=0.332。

仍选取上述100条实际地震记录(地震波加速度峰值统一调整为0.3g)对此高层建筑与其裙房进行时程分析，计算在裙房结构顶层高度处的两结构地震最大相对位移。各地震记录计算得到的地震最大相对位移取平均值为12.70 cm。按照本文方法得到的地震最大相对位移为13.51 cm，二者误差为6.38%，说明本文方法较为准确。本例中，裙房高度小于15 m，按照《建筑抗震设计规范》(GB 5001l-2010)［7］所规定的防震缝宽度下限值为10 cm (＜12.70 cm)，如按照此下限值设计防震缝宽度，显然不能满足防止两结构发生碰撞的设计要求，在地震作用下结构碰撞损坏的震害风险增加。

5 结束语

通过对两单自由度体系最大相对位移的研究发现:任意高度比下最大相对位移与周期比的关系曲线介于高度比分别等于1和0两者之间，并可根据上述两种情况进行计算。在此基础上，提出了适用于以第一阶振型为主的相邻多层结构之间以及高层结构与裙房之间防震缝宽度的确定方法。

［1］BERTERO，VITELMO V.Observations on structural pounding，Mexico Earthquakes－1985:factors involved and lessons learned:proceedings of the International Conference［C］.New York:ASCE，1986:264-278.

［2］KASAI，KAZUHIKO，MAISON，et al.Building pounding damage during the 1989 Loma Prieta earthquake［J］.Engineering Structures，1997，19(3):195-207.

［3］清华大学、西南交通大学、北京交通大学土木工程结构专家组.汶川地震建筑震害分析［J］.建筑结构学报，2008，29(4):1-9.

Civil and structural groups Tsinghua University，Xinan Jiaotong University，Beijing Jiaotong University.Analysis on seismic damage of buildings in the Wenchuan earthquake［J］.Journal of Building Structures，2008，29(4): 1-9.

［4］王亚勇.汶川地震建筑震害启示:三水准设防和抗震设计基本要求［J］.建筑结构学报，2008，29(4):26-33.

WANG Ya-yong.Lessons learnt from building damages in the Wenchuan earthquake:three earthquake performance objectives and basic requirements for seismic design of buildings［J］.Journal of Building Structures，2008，29 (4):26-33.

［5］张泾钰.建筑物的变形缝在汶川地震中的反应及对策思考［J］.西华大学学报:自然科学版，2009，28(4): 83-85，108.

ZHANG Jing-yu.Reflections on countermeasures and responses of joints of structures in Wenchuan earthquake［J］.Journal of Xihua University:Natural Science Edition，2009，28(4):83-85，108.

［6］门进杰，史庆轩，陈曦虎.汶川地震对远震区高层建筑造成的震害及设计建议［J］.西安建筑科技大学学报，2008，40(5):648-653.

MENJin-jie，SHI Qing-xuan，CHENXi-hu.Seismic damage of high buildings caused in the ramote areas from epicenter and aseismic design suggestion［J］.Journal of Xi'an University of Architecture＆Technology，2008，40 (5):648-653.

［7］中华人民共和国住房和城乡建设部.GB 50011—2010建筑抗震设计规范［S］.北京:中国建筑工业出版社，2010.

［8］PAPADRAKAKIS，MANOLIS，MOUZAKIS.Earthquake simulator testing of pounding between adjacent buildings［J］.Earthquake Engineering＆ Structural Dynamics，1995，24(6):811-834.

［9］熊海贝，朱伯龙，陆雪平.高层建筑复杂体型设置防震缝的研究［J］.四川建筑科学研究，1996，22(3):27-31.

XIONG Hai-bei，ZHU Bo-long，LU Xue-ping.Study on seismic gaps of high rise building with complex structures［J］.Building Science Research of Sichuan，1996，22 (3):27-31.

［10］KASAI K，JAGIASI A R，VANJ.Inelastic vibration phase theory for seismic pounding mitigation［J］.Journal of Structural Engineering，1996，122(10):1136-1146.

［11］邹宏德，蓝宗建.相邻建筑结构碰撞问题的探讨［J］.工业建筑，2002，32(4):49-52.

ZOU Hong-de，LANZong-jian.Discussion on structural collision between adjacent buildings［J］.Industrial Construction，2002，32(4):49-52.

［12］孟庆利，徐盛增.相邻结构地震碰撞研究简述［J］.世界地震工程，2003，19(4):68-72.

MENG Qing-li，XU Sheng-zeng.A simplified review on the seismic pounding of adjacent building［J］.World Earthquake Engineering，2003，19(4):68-72.

［13］宋天齐.《建筑抗震设计规范》(GB 50011—2001)有关问题研究［J］.工业建筑，2005，35(8):110-113，116.

SONG Tian-qi.Researches on the problems related to“code for aseismic design of buildings”(GB 50011—2001)［J］.Industrial Construction，2005，35(8):110-113，116.

Method for determining seismic gaps width of adacent structures subjected to earthquakes

LU Ming-qi，YANG Qing-shan

(School of Civil Engineering，Beijing Jiaotong University，Beijing100044，China)

Because the width of seismic gaps demanded in the existing seismic design code in China is generally small and lacks theoretical supports，the pounding between adjacent buildings during ground motions may not be avoided completely.The maximum relative displacement between adjacent structures during earthquakes was studied.The effects of period ratio，height ratio were discussed.The maximum relative displacement for any height ratio can be calculated from the two cases that height ratio equals 1 and 0.Based on the conclusion，the method on calculating the maximum relative displacement of adjacent single degree of freedom(SDOF)systems was proposed，and the width of seismic gaps can be also designed.The results by the method are close with those of time history analysis.This indicates that the method is accurate and can be used in the design of the seismic gaps between adjacent buildings.

seismic gap;adjacent structures;period ratio;height ratio;maximum relative displacement;pounding

TU 312.1

A

10.3969/j.issn.1673-5005.2012.01.025

1673-5005(2012)01-0145-05

2011－11－25

国家自然科学基金青年科学基金项目(51008013);山东省交通科技计划项目(2009Y007);中央高校基本科研业务费专项资金资助项目(2009JBM060)

卢明奇(1978－)，男(汉族)，黑龙江齐齐哈尔人，讲师，博士，主要从事工程结构抗震领域的研究。

(编辑 修荣荣)