考虑振动-冲击-摩擦的旋转叶片动力学特性研究*

王 娇 韩清凯 王相平 陈玉刚 刘尊旭 李学军 沙云东

1 引言

航空发动机属于高速叶轮机械，是复杂旋转机械的典型代表。在实际使用中，航空发动机出现的故障种类繁多，但主要体现为振动故障(vibration fault)[1]。航空发动机振动属于多部件、多层次的振动耦合问题，有效抑制航空发动机的振动，是衡量航空发动机整体性能的重要指标。

作为航空发动机的核心部件，叶片性能直接影响着发动机运行的安全性与稳定性。在中国现役机种中，曾多次出现由于振动过大，导致叶片产生疲劳断裂；由于转子不平衡、不对中或机匣热变形等因素，导致叶片叶尖与机匣发生接触碰撞，出现叶片发生断裂，甚至将外部机匣打穿等事故[2]。因此，实际工况下航空发动机叶片的动力学特性及其振动机理研究，不仅具有重要的学理价值，更具有重要的工程价值。

1.1 叶片动力学模型的研究

发动机在高转速下运转时，由于受到强大离心力作用，导致叶片刚度增加、自振频率增大。准确可靠地预测旋转态下叶片的自振频率(natural frequency)，对于叶片的初始设计及后续维修来说，一直是难以解决的科学问题和工程问题。考虑到以实验方法直接测量旋转态下叶片的自振频率所面临的诸多困难，以数值计算方法研究旋转态叶片在各种振型条件下的自振频率，对于叶片的优化设计具有重要意义[3]。

航空发动机的叶片振动以弯曲和扭转为主，在叶片扭向不大的情况下，解析计算可以采用薄板的弯曲和扭转理论来计算叶片的振型和自振频率。而大多数叶片的叶高与弦长之比较大，此时弯曲振动(bending vibration)是叶片最容易发生且最危险的一种振动(见图1(a))，因而可以将叶片视为变截面梁(beam with non-uniform cross-section)或等截面梁(beam with uniform cross-section)。另外，由于安装叶片的轮盘刚度相比于叶片刚度，要大很多，故可以将叶片根部的边界条件近似为悬臂状态(见图1(b))。所以，在实际研究中，为了简化分析，一般将旋转态下的叶片等效为旋转悬臂梁模型(Rotating Cantilever Beam Model，RCBM)[4-6]。

图1 叶片等效为悬臂梁示意(一阶弯曲)

旋转悬臂梁(rotating cantilever beam)区分于非旋转梁(non-rotating beam)的本质特征是，除了结构由弹性变形产生的加速度，运动方程可能涉及陀螺效应(gyroscopic effect)、科氏力(Coriolis force)和向心加速度(centripetal acceleration)等。同时，旋转系统的刚度特性相比于静止状态会发生变化，即产生离心刚化效应(centrifugal stiffening effect)。

1921年，Southwell等学者[7]基于瑞利能量法(Rayleigh energy method)估算旋转态下梁的固有频率，提出了著名的索恩维尔方程(Southwell Equation，SE)，至今仍在工程上被广泛应用。后来，Schilhansl[8]提出了局部线性的弯曲梁模型(Partially Linear Bending Beam Model)运动方程，将里茨法(Ritz Method)应用于SE，可以获得更加精确的计算结果。但由于当时数值计算技术的限制，Schilhansl提出的方法没有得到数值计算的验证。

随着计算机技术和数值计算方法的发展，旋转梁的理论研究取得了飞速发展，学者们应用数值方法进行了大量的研究，更复杂的形状和更多的影响参数被引入旋转梁模型之中[9-11]。其中，广泛应用于结构瞬态响应(transient response)的是经典线性模型(Classical Linear Model，CLM)[12-13]。CLM采用笛卡尔变形变量(Cartesian Deformation Variables)和线性柯西应变(Linear Cauchy Strain)，具有节省计算内存空间、计算精度高等优点。但是，当结构发生整体运动时，CLM会产生错误的结果。

为了解决CLM的问题，学者们提出了一些非线性建模方法，这些方法可以得到更加精确的解。Hodges[14]应用瑞利商法(Rayleigh quotient method)直接求解旋转态下不均匀分布悬臂梁的固有频率和不连续载荷的响应。Yeh等学者[15]通过Galerkin法研究了锥度比(taper ratio)、弹性约束(elastic constraint)、末端质量(tip-mass)、安装角度(installation angle)和旋转速度(rotating speed)等因素对变截面旋转梁(rotating beam with nonuniform cross-section)振动特性的影响。但是，由于存在非线性，计算效率非常低下。

近年来，随着有限单元法(Finite Element Method，FEM)和相关有限元软件的飞速发展，以及计算机性能的提高，基于有限元法的旋转悬臂梁模型(RCBM based on FEM)也随之兴起，旋转悬臂梁模型的研究进入了一个全新的发展时期。

Chung等学者[16]应用有限单元法求解了旋转悬臂梁模型的固有频率，用拉伸变形模型(Stretch Deformation Model)取代轴向变形模型(Axial Deformation Model)，考虑了拉伸和翼弦方向变形的相互耦合，基于哈密顿变分原理(Hamilton variational principle)建立方程，研究了固有频率随转速的变化，计算了给定转速下悬臂梁变形和应力的分布，研究了不同转速对悬臂梁变形和应力分布的影响。Ozgumus等学者[17]应用包含了平面弯曲振动和扭转振动耦合运动状态的双锥形Timoshenko梁模型(Biconical Tapered Timoshenko Beam Model)，采用哈密顿变分原理建立了包括旋转半径(radius of gyration)、角速度(angular velocity)、转动惯量(rotational inertia)、剪切力(shear force)、泊松比(Possion ratio)、扭转应力(torsional stress)、锥度比等参变量的联合运动方程，引入变分法求解运动方程(Kinematic Equation)，研究了上述参变量对于旋转态梁模型固有频率的影响。Lee等学者[18]提出了基于Euler-Bernoulli梁理论的悬臂梁模型近似代替旋转态下的叶片进行试验，发现旋转态下的离心刚化效应对于悬臂梁模型固有频率的影响很大，并描绘了悬臂梁频率变化曲线。

Banerjee[19]在有限元方法中引入动刚度矩阵(Dynamic Stiffness Matrix，DSM)，研究了Euler-Bernoulli梁模型的自由弯曲振动。相比于传统有限元方法，引入DSM后具有很多优势，特别是需要得到更加精确结果和更高计算频率时。因为采用DSM的解是基于单元微分方程的闭环形式的解，所以其结果可以称得上是准确的。

动态有限元法(Dynamic Finite Element Method，DFEM)是由Hashemi等学者[20]提出的，可以看作是加权残量法(Weighted Residual Method)和DSM的结合。Hashemi采用DFEM，建立了受陀螺效应和科氏力影响的均质旋转梁(uniform rotating beam)的精确方程，利用虚功原理(principle of virtual work)、近似变量节点(approximate variable node)和动态型函数(dynamic shape function)得到了厄米共轭(Hermite conjugate)的且与质量属性相关的刚度矩阵(stiffness matrix)，分析了梁单元频率受刚度矩阵的影响问题；通过Wittrick-Williams算法得到了科氏力对于旋转态悬臂梁频率影响的数值解。

1.2 叶片-机匣结构研究

在航空发动机中，以轴流式压气机(axial-flow compressor)为例，主要有两个组成部分。一是以转轴为主体的可转动部分，称为压气机转子(compressor rotor)，包括安装在轮盘(disc)随转轴(shaft)一起旋转的转子叶片(rotor blade)；二是机匣(casing)和安装在机匣上的静子叶片(stator blade)，称为压气机静子(compressor stator)(见图2)。

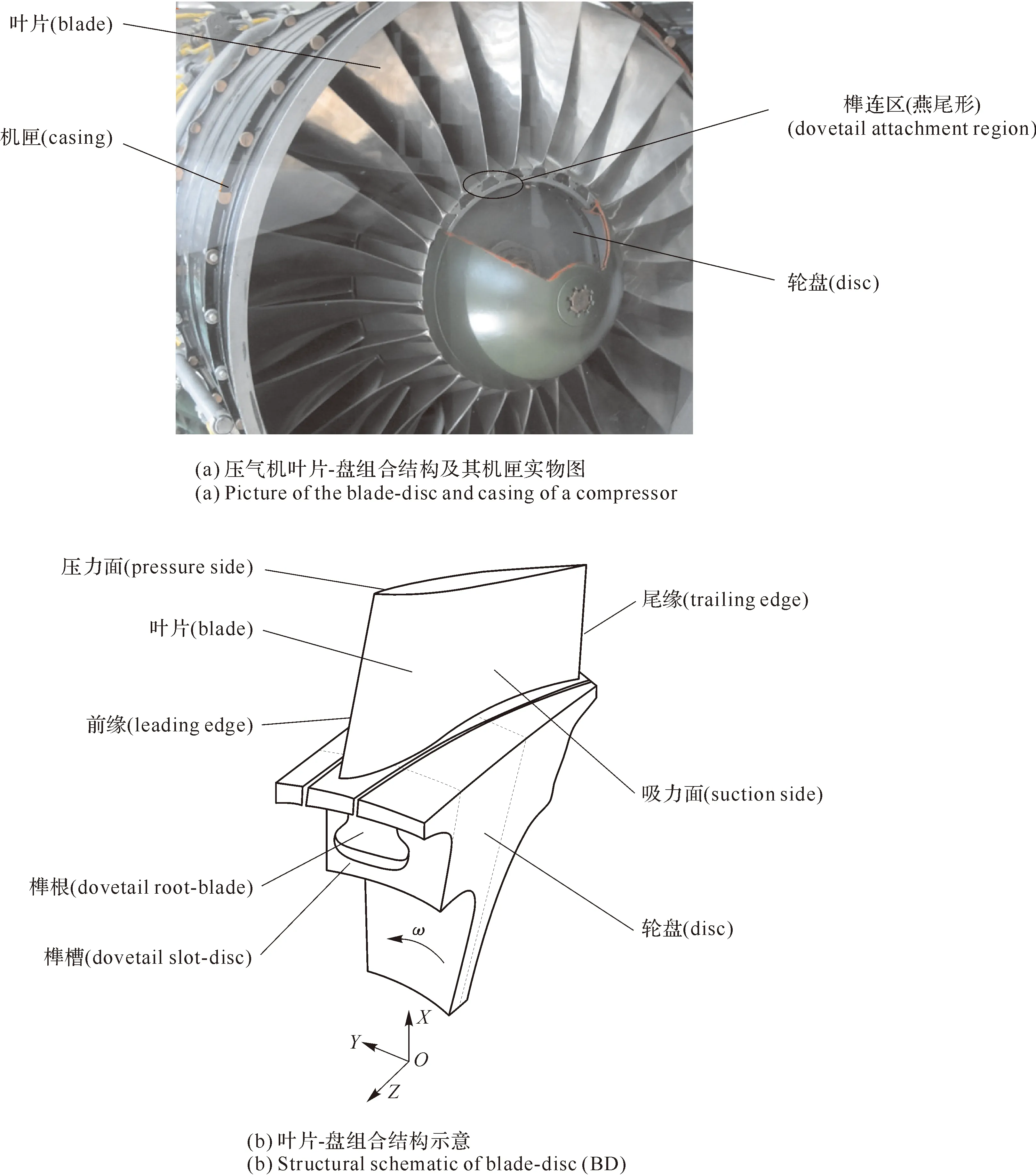
图2 压气机叶片-盘组合结构及其机匣

采用榫根(dovetail root-blade)和榫槽(dovetail slot-disc)连接的叶片和轮盘的组合结构(见图2b)，本文称为叶片-盘组合结构(Blade-Disc，BD)。

由于设计、制造及安装等问题，导致发动机转子不对中或不平衡；机匣受热不均匀(即存在热梯度)，导致机匣产生热变形；发动机在实际运转状态下受到的空气气流作用，以及发动机转子出现裂纹等因素，均会激发转子部件、BD和机匣等部件的局部振动，引起部件变形。由于叶片叶尖与机匣之间的初始间隙是安装时预定的，在前述因素导致部件变形时，叶片与机匣之间可能会发生接触，从而产生接触力并产生耦合作用，使得整个系统呈现出强非线性的动力学特性[21]。

通常，以下两种工况可能会导致叶片与机匣发生接触碰撞(contact collision)[22-23]。

(1) 稳定工况 指发动机转子系统以某一稳定转速工作。此时叶片受到强大的离心力和气流激振力(airflow induced force)，加之转子不对中不平衡等因素，将引起发动机叶片沿轴向伸长和振动，而外部机匣在实际工况下会发生热变形。两部件的局部振动最终会导致叶尖与机匣发生接触碰撞，这使得叶片承受很高的接触应力，过大的接触应力甚至会引起叶片断裂，断裂的叶片有时会击穿外部机匣，造成重大事故。

(2) 过渡工况 指发动机起动、加速、减速、刹车等工作状态。发动机过渡工况一般不超过数个毫秒(ms)，此时叶片-机匣结构受到强大的冲击。例如，航空发动机由工作状态转向停车时，发动机转子将经历极大的速度变化过程，此时叶片可能因承受巨大载荷而致使叶片与机匣发生碰撞。

另外，为了提高航空发动机的工作效率，通常在设计时会减小叶尖与机匣之间的间隙，轮盘会采用适当锥度，以减小叶片和机匣之间寄生气流(parasitic airflow)的流动[24]。但是，在减小叶片与机匣之间间隙的同时，不可避免地增加了叶片叶尖与外部机匣发生接触碰撞的几率。

因此，寻找一种能够描述叶片叶尖与机匣之间接触碰撞问题的理论模型，有利于更好地解析BD与机匣之间振动耦合的物理本质，对于航空发动机的设计、故障诊断和维修都有着重要的理论指导意义。

目前，针对叶片与机匣接触碰撞问题，能够检索到的研究文献甚少，并且尚未见到确切的数学模型。已有的研究论文，多集中于带叶片的转子与机匣的碰撞。

近年来，国外学者提出采用旋转梁模型(Rotating Beam Model，RBM)和圆筒模型(Cylinder Model)相结合的方法，来模拟叶片与机匣的碰撞过程。

Sinha[25]研究了带叶片的柔性转子与刚性机匣的碰撞动力学特性，将叶片简化成旋转态Euler-Bernoulli梁模型(Rotating Euler-Bernoulli Beam Model，REBBM)，并引入由陀螺力矩(gyroscoopic torque)引起的弯曲变形，发现当叶片叶尖与机匣发生接触时，接触力类似于Hertzian接触产生的力。随后，Sinha[26]提出基于旋转的Timoshenko梁模型(Rotating Timoshenko Beam Model，RTBM)理论，考虑离心刚化效应并在梁顶部添加周期性脉冲驱动力模拟叶片与机匣的碰撞产生的库伦力(Coulomb force)，应用数值方法分析了悬臂梁与机匣在不同摩擦参数和接触时间的作用下对于叶片频率的影响，以及悬臂梁的非线性响应特性，发现相较于旋转态Euler-Bernoulli梁模型(REBBM)，旋转的Timoshenko梁模型(RTBM)更能精确地反映出长细比叶片的振动情况。Lesaffre等学者[27-28]提出了叶片与机匣的接触模型，将叶片简化成旋转态Euler-Bernoulli梁模型(REBBM)，并进一步简化成具有两自由度的集中质量模型(Lumped Mass Model，LMM)，将机匣简化成柔性环(flexible ring)，研究了转子叶片转速大于临界转速时引起的机匣-叶片系统不稳定现象，通过研究系统的频率变化，得到了叶片-机匣系统的碰撞特性。

Legrand等学者[24]引入了机匣与叶片-盘组合结构(BD)的二维模型，研究了机匣与BD的k节径模态的一致特性，很好地预测了发动机在不同转速下机匣与叶尖之间的接触现象，并采用Lagrange乘子法研究了机匣与叶尖的接触特性，应用一种改进的时间精确积分法对考虑接触后的动力学方程求解，预测了叶片与机匣在接触后可能发生的阻尼振动(damping vibration)、连续运动(continuous movement)，以及分散运动(decentralized movement)等动力学行为。

Batailly等学者[29]对叶片-盘组合结构(BD)与机匣分别进行直梁模型和曲梁模型的简化，为减少计算量，采用模态坐标转化方法将离散后的多自由度方程简化为少自由度方程，研究了基于Lagrange乘子法的机匣与叶尖之间的相同模态下的碰摩理论(Modal Interaction Theory，MIT)，并提出了“直接接触法则”(Direct Contact Law，DCL)。

针对发动机叶片叶尖与机匣的碰撞摩擦问题，国外制造商采用在机匣内侧喷涂软涂层的办法调整叶片与机匣的间隙，以减少叶尖与机匣之间直接的刚性接触碰撞。虽然这种方法已是国外学者研究的热点[30]，且在实际应用中取得了良好的效果，但目前对可磨耗涂层与叶尖之间的接触摩擦机理还尚不清楚。

1.3 叶片-盘组合结构(BD)振动耦合问题

在航空发动机中，叶片通常是通过叶根榫头与轮盘榫槽联接在一起的。航空发动机工作时，在离心力作用下，榫槽与榫头紧密接触，实现叶片随轮盘的高速旋转。榫槽与榫头的联结结构有多种形式，例如，燕尾形(dovetail)榫根与榫槽(见图2)、枞树型(fir-tree)榫根与榫槽(见图3)，等等。一方面，燕尾形或枞树形榫根结构都包含接触表面，在发动机实际运行中，这些表面之间会发生接触摩擦。另一方面，由于轮盘上的叶片总是整数且沿周向均布，所以BD具有循环对称(cyclic symmetry)的特点。

图3 自带冠涡轮叶片-盘组合结构

对于BD的动力学设计与分析，传统方法一直是将叶片和轮盘各自作为一个单独的部件进行动力学分析，或者是将叶片与轮盘当作一个整体进行研究。这一方法没有考虑叶片与轮盘之间的接触摩擦，势必导致设计参数与实际工况不符，因而可能引发严重的事故。因此，对具有接触摩擦特性的BD进行固有特性分析，研究BD的共振特性，对于BD的优化和振动安全评估具有重要意义。

国内外学者对转子组合结构的振动模态进行了大量研究。Srinivasan[31]对BD的振动问题进行了综述，并将叶片的振动划分为由结构引起的振动和由气流激振力引起的振动等两类问题。Crawley等学者[32]的研究阐述了叶片的节径振动与转子振动之间的耦合关系，结果表明，叶片的低节径振动与转子的振动互相耦合，叶片的高节径振动与转子之间没有关系，主要表现为叶片的高阶振动。Chun等学者[33]建立了BD的数学模型，考虑离心力、科氏力、陀螺力矩对耦合系统振动的影响，结果表明叶片的扭转角(torsion angle)和交错角(alternate angle)的变化都会对BD的振动特性产生影响。周传月等学者[34]在考虑到离心力及材料参数随温度变化的情况下，利用NASTARN对船用燃气轮机BD的固有特性影响进行了研究，并与实验数据进行了对比，取得了较好的一致性。秦飞等学者[35]考虑到叶片变形的几何非线性和叶根接触非线性，研究了枞树型叶根尺寸误差对叶片固有频率的影响，并指出考虑叶根和轮盘之间的装配接触研究是必要的。

1.4 自带冠叶片(ISB)减振研究

在航空发动机实际工况下，即使是稳定运转，叶片仍会由于气流激振力等作用而产生振动，当激振力频率落在发动机叶片自振频率区域时，叶片会产生共振现象(resonance phenomenon)[36]，将会因振动量过大而导致失效。为此，以降低叶片疲劳破坏(fatigue failure)几率为目的，设计者常采用诸如带凸肩叶片(shrouded blade)、自带冠叶片(Integrally Shrouded Blade，ISB)等减振结构以降低叶片动应力(dynamic stress)。

ISB(见图3)的叶冠间接触碰撞摩擦减振结构因具有减振效果好、安装检修方便、制造精度低等优点，已在航空发动机等领域获得广泛应用[37]。实际装配中，ISB相互之间位置结构有两种。一种是运行状态下叶冠保持紧密配合，称为紧配型ISB(Close-Fitting ISB)。这种自带冠叶片在运行状态下由于弹性扭转恢复使叶冠间保持紧密配合，依靠接触面之间相互滑动消耗能量实现减振。另一种是在相邻叶片叶冠之间预留一定的初始间隙，称为间隙型ISB(ISB with Initial Gap)。若叶片振动的幅值超过叶冠间隙，则相邻叶冠之间会发生碰撞摩擦。间隙型ISB通过冠间的碰撞限位作用来减小叶片振动的振幅，同时冠间的相互摩擦会将振动的能量转化为热能以耗散叶片振动产生的能量，从而起到抑制叶片振动的作用，在实际中应用最广泛、最成功。

叶冠之间的碰撞摩擦属于非线性动力学行为(nonlinear dynamic behavior)，再加上ISB本身的复杂特性，虽然关于自带冠阻尼结构(integrally shrouded damping structure)对叶片减振的效果已经有了初步定性的结论[38]，可用来指导阻尼结构的优化设计，但从已发表的文献看，目前尚未有学者提出统一模型，以模拟多参数(如叶冠初始间隙(initial gap between shrouds)、接触弹性系数(contact elastic coefficient)、冠间摩擦系数(friction coefficient between shrouds)、接触角(contact angle)，等等)影响冠间的接触碰撞特性。因此，自带冠叶片(ISB)结构的减振机理、参数影响的程度等缺乏更深入的理论研究，还有许多问题需要解决。

一些学者通过采用施加限位约束作用的梁模型振动，模拟叶片叶冠的碰撞特性，取得了一些成果。武新华等学者[37]将ISB等效为弹簧-质量模型(Spring-Mass Model)，叶冠间的接触碰撞简化为有间隙的弹簧-干摩擦阻尼模型(Spring-Dry friction Damping Model)，建立了叶冠碰撞动力学方程(dynamic equation of collision between shrouds)，通过特性分析证明了当叶冠的相对位移大于叶冠的间隙时，叶冠碰撞有减振作用，并且振幅随间隙减小而减小。Nagasawa等学者[39]研究了叶片碰撞侵入与叶片表面硬度的关系，提出了冠间接触碰撞动力学方程，并通过不同材料对提出的模型进行了验证。马晓峰等学者[40]利用弹塑性理论建立叶片碰撞弹性力模型(Collision Elastic Force Model)，应用Herbert直接法建立碰撞阻尼力模型(Collision Damping Force Model)，对冠间接触碰撞的非线性动力学模型进行数值模拟，分析了ISB冠间接触碰撞(contact collision between shrouds)的非线性动力学特性。徐大懋等学者[38]对多种间隙型ISB模型进行了长期研究，提出了叶冠碰撞理论模型(Theoretical Model of Collision between Shrouds)，并通过实验验证了减振效果与叶片形状参数有关。李剑钊等学者[41]通过叶片边界非线性研究，提出了带有碰撞阻尼的叶片三维实体有限元模型(Finite Element Model of the Three-dimensional Blade Entity with Collision Damping)，并实验验证了计算模型的精度，发现随着叶冠间隙、激振力频率及激振力振幅的增加，叶片出现明显的频谱分量。南国防等学者[42]认为ISB的减振主要是通过冠间的碰撞和摩擦组合运动实现的，建立了ISB带间隙的弹簧质量模型(Spring-Mass Model with Gap)，采用Sgn摩擦模型(Sgn Friction Model)建立叶冠碰撞系统(shroud collision system)的动力学模型，探讨了叶冠初始间隙等参数对减振效果的影响。Pennacchi等学者[43]推导了单个叶片受到气体激振力(FIF)的响应方程，通过实验和有限元软件进行仿真分析，并通过多个叶片并排连接模拟带间隙的叶片组，经过试验分析测量了带间隙叶片的碰撞对叶片响应的影响。

1.5 本文的研究思想与理论架构

从上述文献可以看出，针对航空发动机叶片，以往的研究大多是针对某一局部问题(例如，单一叶片结构、叶片与某些部件之间的接触碰撞及其振动耦合，等等)而展开，没有形成一个系统的研究框架。

本研究团队在已有研究中，曾针对以航空发动机为代表的高速旋转机械的振动问题，提出了由系统级建模与振动分析、部件级建模与振动分析、零件级建模与振动分析组成的多层次振动分析方法(Multi-Level Modeling Method for Vibration Analysis，MLMMVA)[44]，形成了新的机械结构与系统的振动分析和动态设计方法体系[45]。在振动分析模型方面，强调采用理论解析、有限元数值仿真和实验验证，相互对比、相互确认；在振动分析内容方面，强调采用固有特性分析(包括静止态和旋转态)及其结构参数和工艺参数影响分析；在机械结构和系统层次上，强调系统振动响应分析，以及带故障结构和系统的振动响应分析和非线性振动分析[46]。

在航空发动机旋转叶片动特性研究中，无论叶尖与机匣的碰撞和摩擦、ISB叶冠的接触碰撞，以及叶根榫头与轮盘榫槽之间的接触摩擦，都与振动有着直接关系。因此，本研究团队提出，航空发动机叶片等旋转结构件与其他构件的碰撞、摩擦与振动具有强烈的耦合性质，在动特性分析和振动分析时，必须加以综合考虑[47]。对于旋转叶片动特性研究，需要基于碰撞和摩擦特性，进行解析模型和有限元模型的建立，研究各构件之间的振动耦合关系对叶片动力学特性的影响。

基于以上认识理念，本研究团队重新组构了叶片动力学特性分析的基本理论和方法(包括本文研究的主要结构、叶片振动的类型和振型、叶片动力学特性分析的基本要素，等等)，通过经验公式，基于连续体的解析模型和有限元模型研究了旋转态下叶片的固有特性；采用梁模型研究了叶片-盘组合结构(BD)与机匣的节径振动模态，提出了BD与机匣的质点模型并建立了系统动力学方程，采用数值算例计算了叶尖与机匣的接触间隙；在考虑和不考虑叶片榫头和轮盘榫槽的接触摩擦特性等两种条件下，使用ANSYS对BD的固有特性进行了分析，研究了叶根接触摩擦特性对BD固有特性的影响；建立了叶冠间接触碰撞的弹性碰撞力和阻尼力模型，进而应用于叶冠间碰撞的连续体模型和有限元模型，并采用数值算例研究了叶片转速、叶冠间初始间隙和叶冠间接触刚度等对ISB振动响应特性的影响等，研究了干摩擦阻尼减振的效果，其研究框架见图4。

图4 考虑振动-冲击-摩擦的航空发动机叶片动力学特性分析研究架构

2 叶片动力学特性分析基本理论

2.1 叶片振动的类型及振型

叶片振动类型有很多种，按激振力(exciting force)的有无及其特点可以分为自由振动(free vibration)、强迫振动(forced vibration)和自激振动(self-excited vibration)等3种基本振动形式[48]。

然而，由于气体尾流激振力(wake vibration force)和旋转失速(rotating stall)造成的气流激振力(airflow induced force)等原因，使得在实际工况下，叶片一般以强迫振动和自激振动为主。

一般来说，叶片振型(modal shape)包括弯曲(bending)、扭转(torsion)和复合振动(combined vibration)等3类。由于现实中的所有叶片，其相邻截面上的主惯性轴(principal axis of inertia)并不在同一平面内，叶片振动实质上都属于复合振动，并不存在纯弯曲振动(pure bending vibration)或纯扭转振动(pure torsional vibration)等情况。

2.1.1 叶片振动的类型

2009年9月26日，《扬子晚报》等媒体报道称，吴浈曾经专程到江苏延申公司视察、指导甲流生产，帮助企业顺利完成研发、生产等工作。

【定义1自由振动(free vibration)】 振动系统在无交变外力作用下发生的简谐振动(simple harmonic vibration)。

自由振动的频率仅取决于振动系统的物理参数。对于单自由度系统(single DOF system)，振动频率取决于系统的质量和刚度等参数；对于多自由度系统(multi-DOF system)，取决于系统的质量矩阵(mass matrix)和刚度矩阵(stiffness matrix)，亦可看成取决于系统的边界条件、几何形状与材料参数。

【定义2强迫振动(forced vibration)】 振动系统在周期性交变外载荷或位移作用下所产生的振动。

强迫振动是由外界激振力激起的，且以外界激振力的频率振动。例如，气体尾流激振力(见图5)和旋转失速造成的气流激振力(见图6)导致的叶片振动均属强迫振动[48]。

当外界激振力的频率与结构固有频率相同时，振动系统会产生强烈振动——共振。

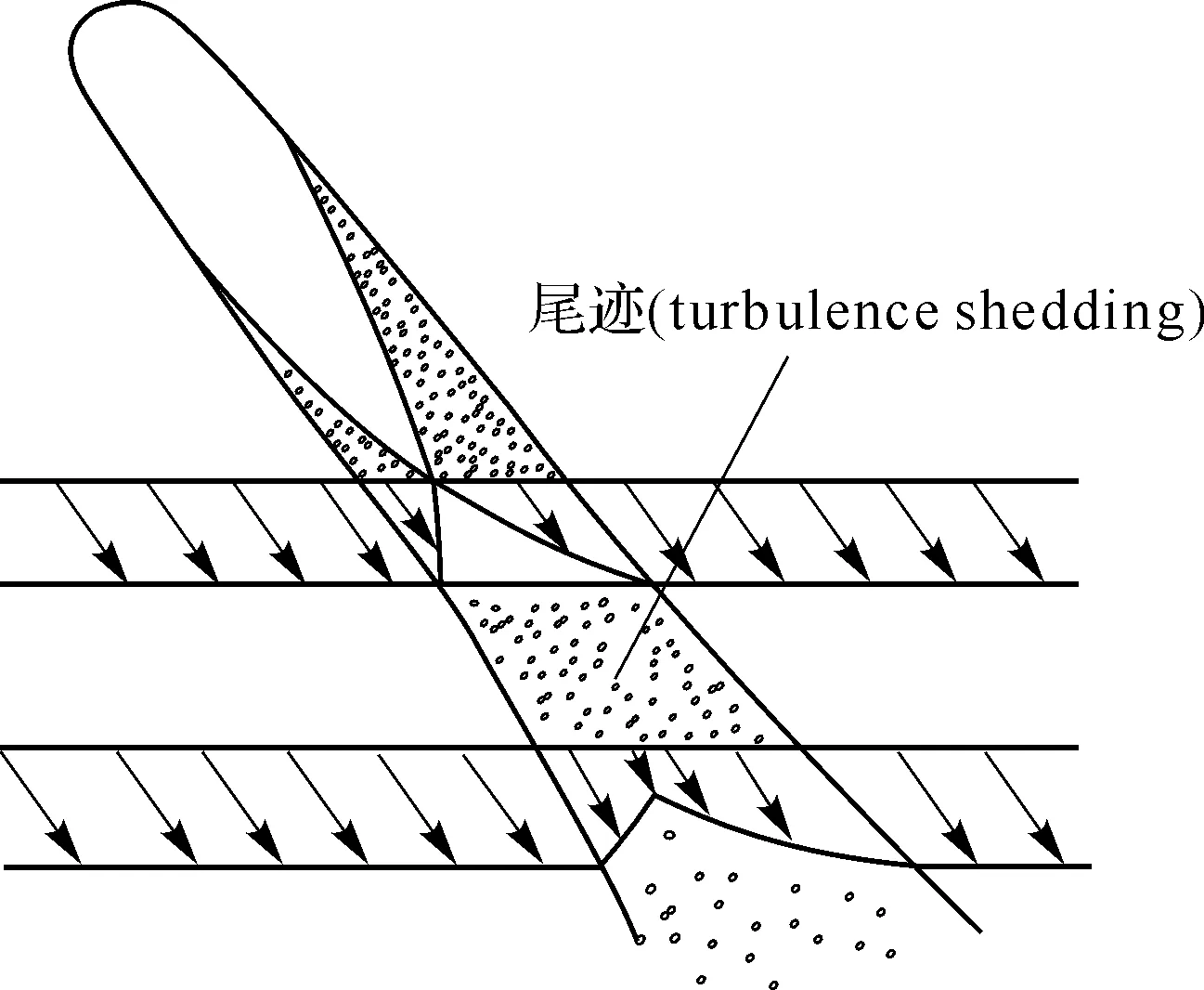
图5 尾迹的形成

图6 旋转失速

【定义3自激振动(self-excited vibration)】 受自激力作用所产生的振动。

自激振动不同于自由振动和强迫振动，这种振动不是由周期性外载引起的，而是因结构或工作条件等原因由气流所诱导的振动。一旦出现这种振动，系统会不断地从气流中吸取能量而激发系统自身的振动。如果振动系统的阻尼耗能(damping dissipation energy)不足以抵消系统所吸收的能量，则随着能量的不断积累，振幅会越来越大，振动应力也迅速增大，很快会因系统的振动疲劳而致使结构出现裂纹，乃至断裂。叶片颤振(blade flutter)即属于自激振动。

2.1.2 叶片振动的振型

由于叶片高速旋转，激振条件复杂，叶片的几何型面扭曲，以及机组经常在变动工况下运行，实际工况下的叶片振动并不是单纯的弯曲振动或扭转振动，而是弯曲振动、扭转振动等多种振动的复合振动。

为了方便研究，可将主要表现为弯曲变形的复合振动近似看作弯曲振动；将主要表现为扭转变形的复合振动近似看作扭转振动；将弯曲与扭转等两种变形成分都较大的振动称为复合振动[48]。以平板无扭向的叶片(自然状态)(见图7(a))为例，定义以下振动形式[3, 48]。

【定义4切向弯曲振动(tangential flexural vibration)】 叶片绕其截面最小惯性轴产生弯曲变形的振动(见图7(b))。

叶片上出现一条横节线的弯曲振动称为一阶弯曲振动(first-order bending vibration)，相应的频率为一阶弯曲振动频率(first-order bending vibration frequency)；出现两条横节线的弯曲振动称为二阶弯曲振动(second-order bending vibration)，相应的频率称为二阶弯曲振动频率(second-order bending vibration frequency)，依次类推。

【定义5扭转振动(flexural vibration)】 叶片围绕沿叶片高度方向通过截面重心的轴线而振动(见图7(c))。

无扭向的平板叶片做扭转振动时，叶片上出现一条纵向节线。叶片上具有一条纵向节线和一条靠近叶根的横向节线的振动称为一阶扭转振动(first-order torsional vibration)，相应的频率为一阶扭转振动频率(first-order torsional vibration frequency)；具有一条纵向节线和两条横向节线的振动称为二阶扭转振动(second-order torsional vibration)，相应的频率称为二阶扭转振动频率(second-order torsional vibration frequency)，依次类推。

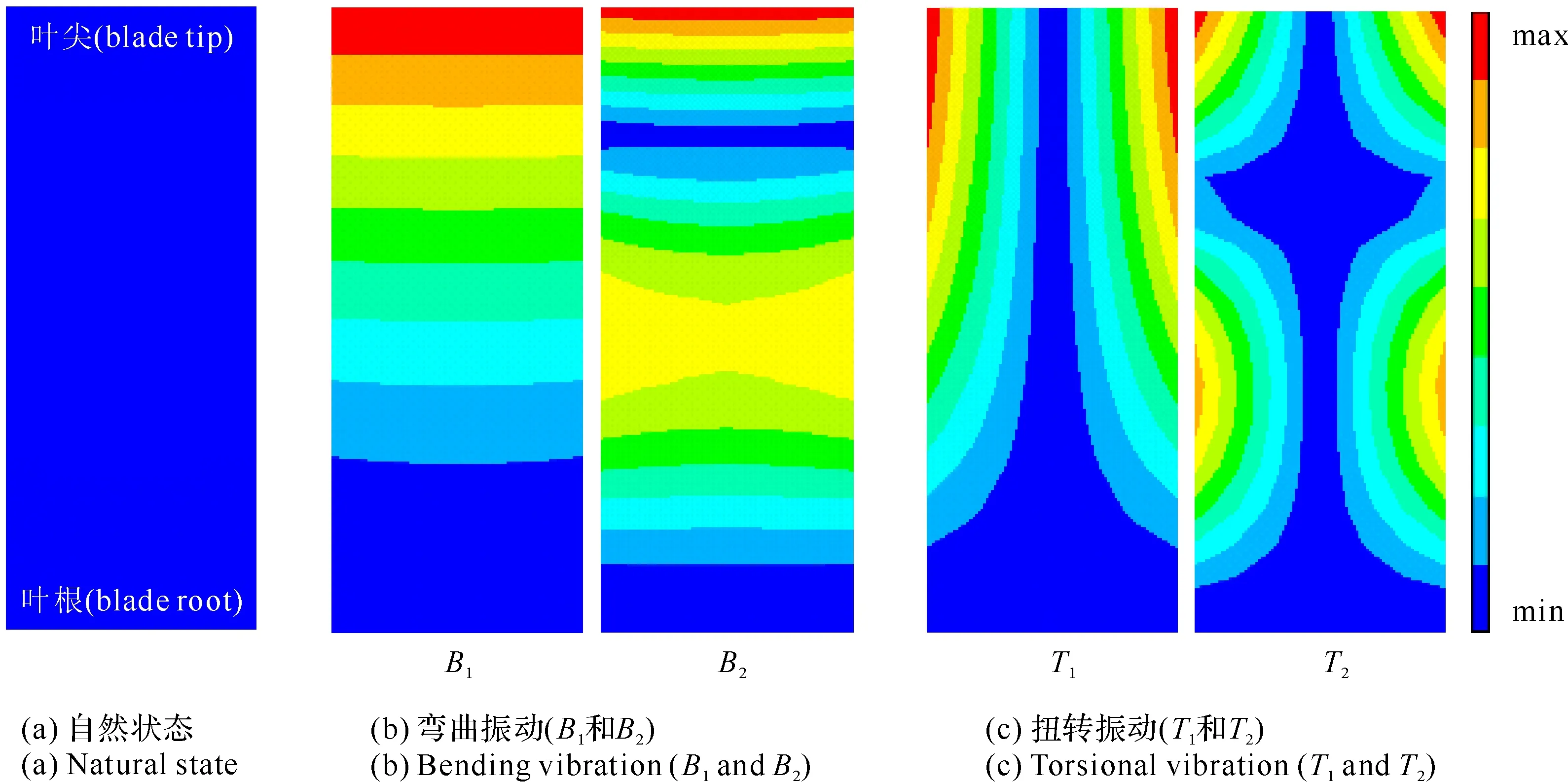
图7 无扭向平板叶片振型

还有另一种叶片振型分类方式[3]。

【定义6A型振动(type A vibration)】 叶根不动，叶顶有位移的振动形式(见图8)。

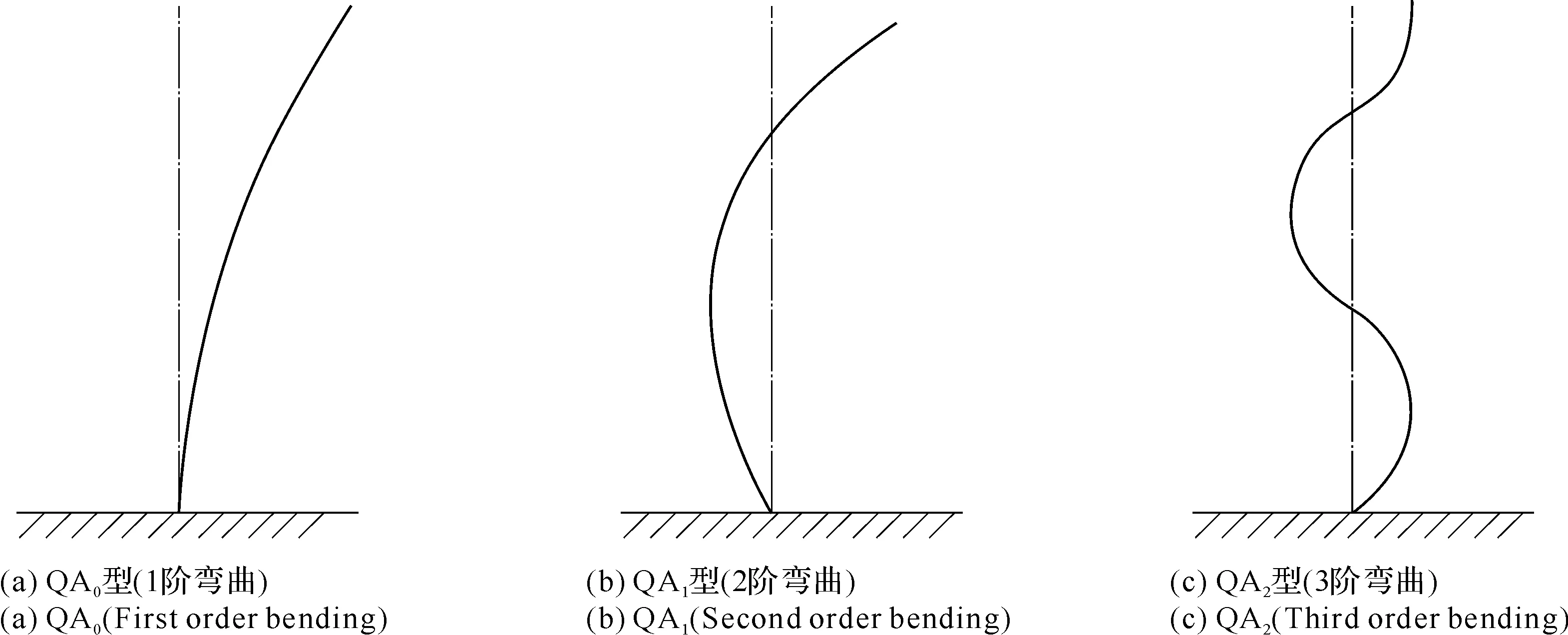
图8 叶片QA型振动振型示意

A型振动可以分为切向和轴向两种，切向A型振动用QA表示，轴向A型振动用ZA表示。实际应用中，QA型振动常简写为A型振动。

叶片作QA型振动时，也有下列各种不同的型式，各自对应着相应阶次的自振频率。常用下角标数字表示振动节点(线)数。

【定义7QA0型振动(type QA0vibration)】 沿叶片全长都有位移，叶顶幅值最大，自叶顶至叶根振幅渐渐减小的振动形式。

叶片的QA0型振动频率通常是叶片最低阶自振频率，即叶片的第一阶自振频率，故QA0型振型通常是叶片的第一阶振型。

【定义8QA1型振动(type QA1vibration)】 沿叶片高度有一处不振动，或者习惯上说有一个节点；在叶顶处振幅最大，由叶顶向下振幅逐渐减小，至节点处为零。然后振幅又逐渐增大(但方向相反)，达到另一最大值后再逐渐减小，至叶根处又为零。节点上下两部分的振动方向相反，即相位差180°。

叶片作QA1型振动时，叶身上有一个节点。对于等截面叶片，节点位置约距叶根全叶长l的2/3处，而变截面叶片(向上变薄)的节点位置则稍高一些(见图8(b))。

【定义9QA2型振动(type QA2vibration)】 QA2型振动沿叶片高度出现2个节点和3个振幅最大值。

对于等截面叶片，第一个节点约在距叶根0.5l处，第二个节点约在叶顶0.2l处。节点上下两侧振动方向相反，相位角相差180°(见图8(c))。

在实际运行中，更多节点的A型振动很少发生，即使发生，由于频率很高、振幅很小，应力也很低，所以危险性不大，很少加以研究。

2.2 叶片动力学特性分析的基本要素

结构振动主要受其自身固有频率，以及激振力的大小和形式影响，转子叶片振动也不例外。叶片在使用过程中是否会出现振动，主要受其自振频率(固有频率)、激振力，以及叶型(包括进气边缘半径(inlet edge radius)、最大厚度(max thickness)与弦长(chord length)之比、扭心(torsion center)和质心(centroid)的相对位置、最大厚度位置(location of the maximum thickness)、激振力的耦合因素(包括气流攻角(flow angle-of-attack)、压力比(pressure ratio)、扩散因子(diffusion factor)等叶片载荷参数)的影响。

因此，叶片动力学特性分析，首先是振动模态分析(固有频率分析和振型分析)，以及激振力的来源和形式分析；其次是动力加载下的动力学分析。只有这样，才能全面准确地了解叶片的动力学特性(如振动位移、振动应力、碰撞力等)。

2.2.1 叶片的静频率和动频率

【定义10叶片静频率fs(static frequency)】 叶片在不转动情况下的固有频率。

一般地，叶片静频率与叶片长度、横截面面积，以及横截面的惯性矩等几何参数、叶片材料的弹性模量、材料密度等物理参数有关。

【定义11叶片动频率fd(dynamic frequency)】 叶片在旋转态下的固有频率。

叶片动频率fd受工作温度、叶片根部固定装配情况、叶片随轮盘转动的速度等因素的影响，与叶片静频率fs存在较大差异。

航空发动机高速旋转时，叶片受到强大的离心力，叶片无论在旋转平面内或在轴向平面内振动，叶片上任一微元所受的离心力都有促使叶片回到平衡位置的趋向。叶片发生弯曲变形时，其重心偏离通过叶根中心的轴线，这时离心力将对叶片产生弯矩。微元离心力可以分解为径向的dFc1和振动平面内的dFc2、dFc1对叶片产生的弯矩Mc1阻止叶片变形，像弹性力一样使叶片恢复到平衡位置(见图9)。这相当于增加了叶片的弹性恢复力，结果使叶片各阶固有频率有所提高。换言之，叶片动频率比叶片静频率高。因此，只有考虑离心力的刚化效应，实际工作状态下叶片的动力学特性才能得到更加准确的分析[49-51]。

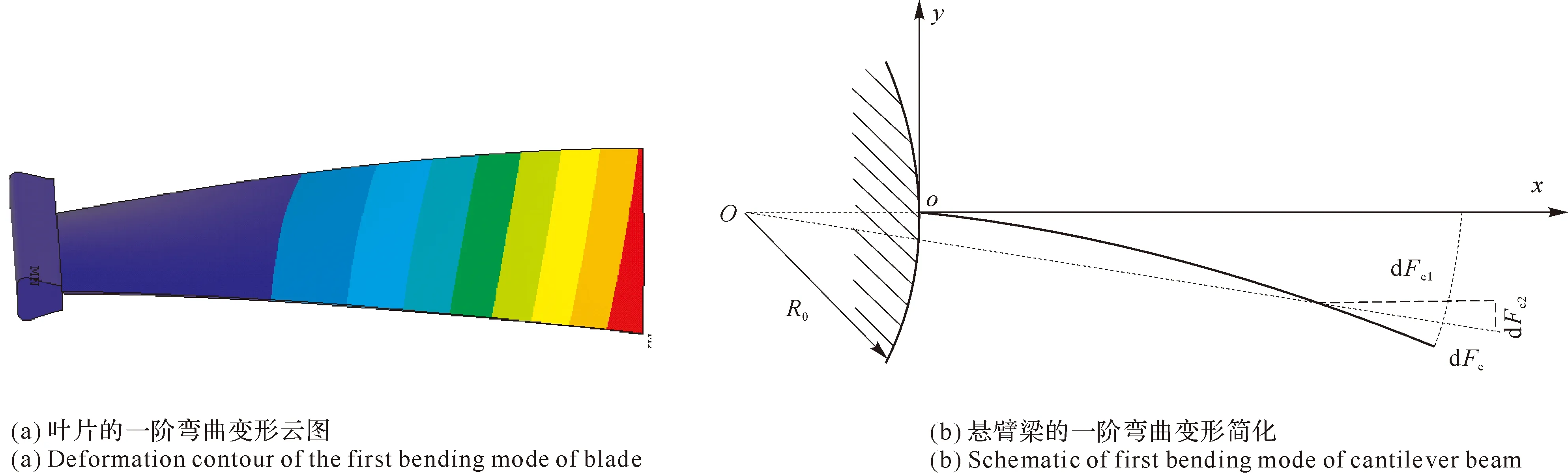
图9 叶片弯曲振动示意

2.2.2 激振力来源及表达式

影响转子叶片振动的因素还有激振力的大小、方向、作用形式，以及与叶型的耦合状态。激振力的形式多种多样，按力学表达形式大体可分为周期性激振力(periodic variation exciting force)、非周期性激振力(aperiodic variation exciting force)(如流体诱发所形成的激振力)和随机激振力(random exciting force)等3类。

对于叶片来说，周期性激振力是主要激振力。这些周期性激振力中，有的是大致按简谐规律变化的，如尾流激振。这类激振力的频率通常与发动机的转速直接相关，因而作用在叶片表面的气动激振力频率可以表达为如下形式。

fe=KΩ/60

(1)

式中，fe为作用在叶片表面的气动激振力频率；Ω为发动机转速，r/min；K为结构系数，如前排叶片数目、失速团数目等。

然而，实际上大多数激振力并不是简谐的。这时，周期性激振力可以看作由多个简谐激振力(simple harmonic exciting force)合成，即周期性激振力可以用三角级数(Trigonometric Serious)展开，表述为如下形式。

Fa(t)=F0+F1sin(ω1t+φ1)+F2sin(2ω1t+φ2)+…+Fnsin(nω1t+φn)

(2)

式中，Fa(t)为周期性激振力；F0为常数项；ω1为基频；φi为不同谐波激振力的相位，i=1，2，…，n,n∈N；F1sin(ω1t+φ1)为第一谐波激振力，即主激振力(main exciting force)；F2sin(2ω1t+φ2)为第二谐波激振力；Fnsin(nω1t+φn)为第n谐波激振力；各阶激振力的频率为ω1的整数倍。

2.2.3 叶片的强迫振动响应分析方法

叶片振动响应分析方法一般包括简化模型解析法(Simplified Model Analytic Method，SMAM)、动力学有限法(Dynamic Finite Element Method，D-FEM)，等等。

【简化模型解析法(SMAM)】 一般是将叶片简化为旋转态梁(板)模型(rotating beam or plate model)，对梁的微元体进行受力分析。

根据动力学平衡原理，列出其运动微分方程，或是对模型的整体势能U和动能T进行分析，结合Hamilton变分式(δ(Tmax-Umax)=0)，导出叶片的运动微分方程，进而利用假设模态法(assumed-mode method)对方程离散，再运用数值计算方法(如Wilson-θ法、Newmark-β法、Newton-Raphson法等)求解离散方程。

【动力学有限元法(D-FEM)】 一般是采用适当的有限元单元(如采用Euler-Bernoulli梁单元或Timoshenko梁单元将叶片简化为悬臂梁)，对叶片的简化模型进行有限元离散。

根据有限元分析理论选择合理的单元位移模式对单元质量矩阵、刚度矩阵，以及等效节点力等进行计算，最后建立整体结构的动力学方程，运用数值计算方法对方程求解，得到叶片的振动响应。

此外，还可以采用商业有限元软件(如ANSYS)对叶片的动态特性进行分析。其步骤有三，一是采用三维建模软件(如SolidWorks、Pro/E、UG等)构造叶片的实体结构模型(见图10(a))，二是将实体结构模型导入有限元软件划分网格(见图10(b))，三是对模型施加约束、载荷和求解(见图10(c)，为叶片受到正弦激振的位移响应)。

图10 叶片实体结构的有限元分析

2.3 碰撞振动响应特征的定性分析

叶片强迫振动达到稳定状态时，其振动响应频率与激振力频率相等。当ISB的叶冠之间发生接触碰撞时，会出现激振力频率的倍频振动(multi-frequency vibration)，这种现象产生的主要原因是碰撞对原有的响应波形产生了“削波”(clipping)[52]。

间隙型ISB的振动为约束振动(vibration with constraints)。在实际作业中，由于部件制造误差和整机装配误差的随机性，因而不能保证叶冠之间的所有间隙均严格相等，因此，实际相邻叶冠间的约束可分为单侧约束(unilateral constraint)、对称约束(symmetric constraint)和非对称约束(asymmetric constraint)等3种情况[40](见图11)。当冠间发生碰撞摩擦时，相应地也有3种不同的碰撞摩擦形式，导致了ISB叶冠出现不同的振动响应特性，这便造成了被“削波”后的振动响应在频谱图上反映出不同的频谱特征。

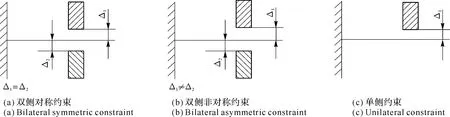
图11 相邻叶片冠间实际碰撞形式示意

2.3.1 单侧碰撞响应特征的定性分析

当叶片发生单侧碰撞时，假定在叶片振动响应的一个周期内，只有当振幅超过间隙初始值时才会发生碰撞。设振动幅值在Ab与-Ab0之间变化，则其运动方程可以表示为如下形式。

(3a)

(3b)

式中，f(t)为振动响应值；t为时间；t1为0时刻开始的半周期内叶片发生正向碰撞结束的时刻；Ab0为未发生碰撞时叶片的稳态振动幅值；Ab为发生碰撞后的振动幅值；ω0为振动响应的频率(此处也是强迫振动的激振力频率)；T0为叶片振动响应的周期，即为叶冠之间发生碰撞的周期；k为整数。

【规定】 在0时刻开始的第一个半周期内，叶片发生碰撞的时间为0～t1(见图12(a))。

式(3)可展开为Fourier级数形式。

(4)

式中，a0为常值分量，即运动的静态分量；an为余弦分量幅值；bn为正弦分量幅值；nω0为n次谐波频率(harmonic frequency)。

由此，可以导出如下参量。

(1) 运动的静态分量

(5)

(2) 基频谐波分量幅值

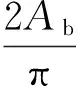
(6)

(3) 其他谐波分量幅值

(7)

(8)

由此可知，叶片发生单侧碰撞时会出现激振力频率及其连续奇偶次倍频的高阶谐波分量，而且幅值逐步减小，这可从图12(b)及后续相关的仿真分析中观察到。

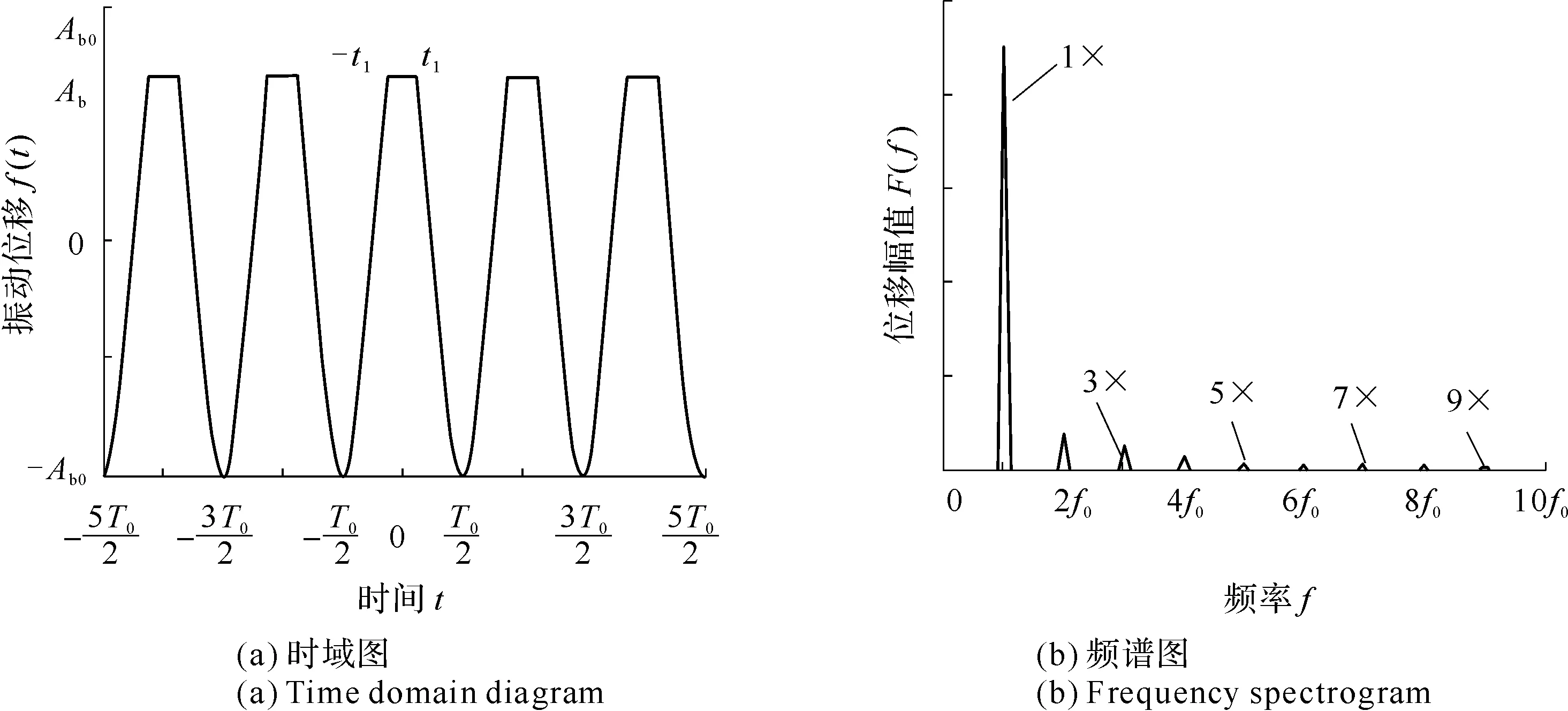
图12 单侧碰撞定性分析

2.3.2 双侧对称碰撞响应特征的定性分析

当叶片发生双侧对称碰撞时，假定幅值在Ab与-Ab之间变化，在0时刻开始的第一个半周期内发生碰撞的时间为0～t1和t2～(T0/2)，则运动方程可以表示为如下形式。

(9)

式中，t2为0时刻开始的第一个周期内叶片发生负向碰撞的时刻；k为整数，k=±(0,1,2,3,…)。

式(9)展开为Fourier级数的形式(见式(4))，可以导出运动的静态分量。

(10)

因为

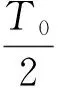
(11)

所以

ω0t1+ω0t2=π

(12)

于是可得

sinω0t2=sin(π-ω0t1)=sinω0t1

(13)

(1) 运动的静态分量

(14)

(2) 基频谐波分量幅值

(15)

(3) 其他谐波分量幅值

(16)

(17)

由式(17)可知，叶片发生双侧对称碰撞时，偶数倍谐波分量幅值为零，只有激振力频率及其奇次谐波分量不为零。反映在频谱图中，即只会出现激振力频率及其奇次倍频的高阶谐波分量，而且幅值也是逐渐减小的，这可以在图13(b)及后续的仿真分析中观察到。

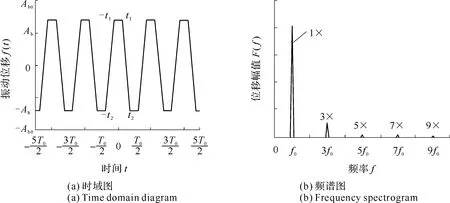
图13 双侧对称碰撞定性分析

2.3.3 双侧非对称碰撞响应特征的定性分析

相邻叶冠间隙在实际工况中是不相等的，在此情况下，叶片会发生双侧非对称碰撞，其理想的运动波形见图14(a)。假定幅值在Ab1与-Ab2之间变化，在0时刻开始的第一个半周期内发生碰撞的时间为0～t1和t2～(T0/2)，则运动方程可表示为如下形式。

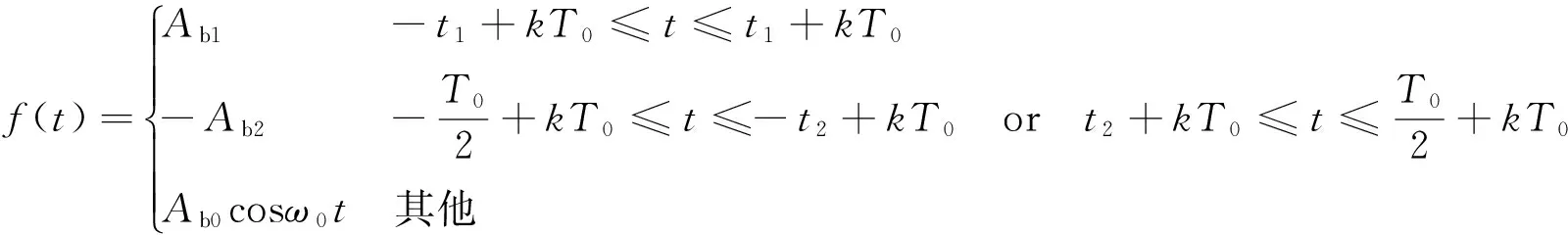
(18)

式中，Ab1和Ab2分别为两侧发生碰撞后的振动幅值；k=±(0,1，2，3,…)。

式(18)可展开为Fourier级数(形式见式(4))，可以导出如下参量。

(1) 运动的静态分量

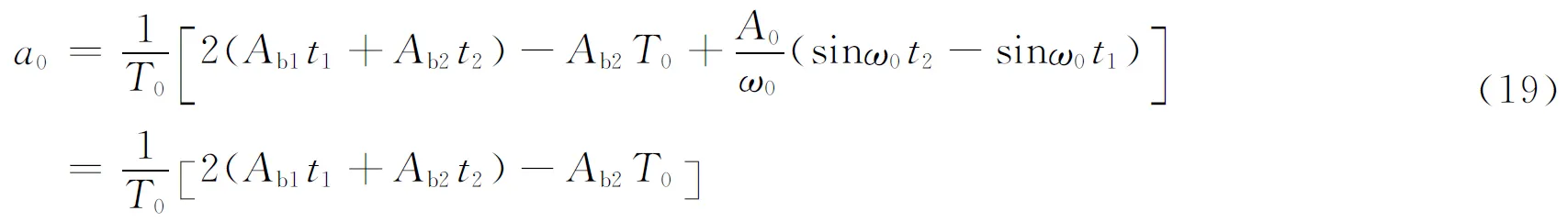
(2) 其他谐波分量的幅值

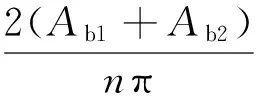
(20)

(21)

由式(18)～式(21)可知，叶片发生双侧非对称碰撞时会出激振力频率及其连续奇偶次倍频的高阶谐波分量，且偶次倍频分量相对奇次倍频分量较小(见图14b)。

图14 双侧非对称碰撞定性分析

3 旋转态下叶片固有特性分析

3.1 基于经验公式的静动频率分析

文献[3]给出了等截面叶片的静频率计算公式。

(22)

式中，fs为静频率，Hz；λi为第i阶特征值；l为叶片工作部分长度，m；E为叶片材料的弹性模量，N/m2；I为叶片横截面惯性矩，m4；ρ为叶片材料密度，kg/m3；A为叶片横截面面积，m2。

由于

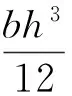
(23a)

A=bh

(23b)

式中，b为叶片宽度，m；h为叶片厚度，m。

所以，静频率计算公式可以改写为如下形式。

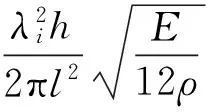
(24)

动频率与静频率之间的关系可以表现为如下形式[3]。

(25)

式中，fd为动频率，Hz；fr为转动频率，Hz；B为叶片动频率系数或速度系数。

在实际工程中，人们根据一些假定条件进行理论推导，得出了一些计算动频率系数B的近似公式，也有根据实验数据归纳得到的一些经验公式。常见的等截面叶片A0型振动的动频率系数B的近似计算公式见表1[3]。

表1 常见的等截面叶片A0型振动的动频率系数

式中，db为叶片中径，m；lb为叶片高度，m。

GE公司对于动频率系数的实验结果如下[3]。

(26a)

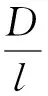
(26b)

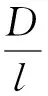
(26c)

式中，Bav为B的平均值；Bmax为B的最大值；Bmin为B的最小值；D为叶轮的平均直径；l为叶片长度。

目前，国内应用最为广泛的叶片A型振动动频率系数的经验公式是ЛМЗ工厂提供的，其A0，A1，A2型振动动频率系数B的近似公式如下[53]。

(27a)

(27b)

(27c)

(27d)

式中，γ为叶片振动平面与叶轮平面的夹角；γ0为叶根振动平面与叶轮平面的夹角；γ1为叶顶振动平面与叶轮平面的夹角。

为了从原理上更好地理解旋转态叶片的动频率，得到更为精确的叶片动频计算方法，本研究团队考虑叶片旋转导致的离心刚化效应(Centrifugal Stiffening Effect，CSE)，将叶片简化等效为旋转悬臂梁(RCB)，忽略科氏力的影响，提出新的叶片动频率计算方法。

根据悬臂梁和有限元基本理论，本研究团队建立了叶片悬臂梁解析模型(Analytical Model of Cantilever Beam，CB-AM)，基于Euler-Bernoulli梁理论的有限元模型(Finite Element Model based on Euler-Bernoulli Beam Thoery，EBB-FEM)和基于Timoshenko梁理论的有限元模型(Finite Element Model based on Timoshenko Beam Thoery，TB-FEM)，对比计算叶片在旋转态下的自振频率(动频率)的结果。

3.2 叶片悬臂梁解析模型(CB-AM)的动频率分析

3.2.1 叶片悬臂梁解析模型的建立

将叶片简化成悬臂梁模型(见图15)。

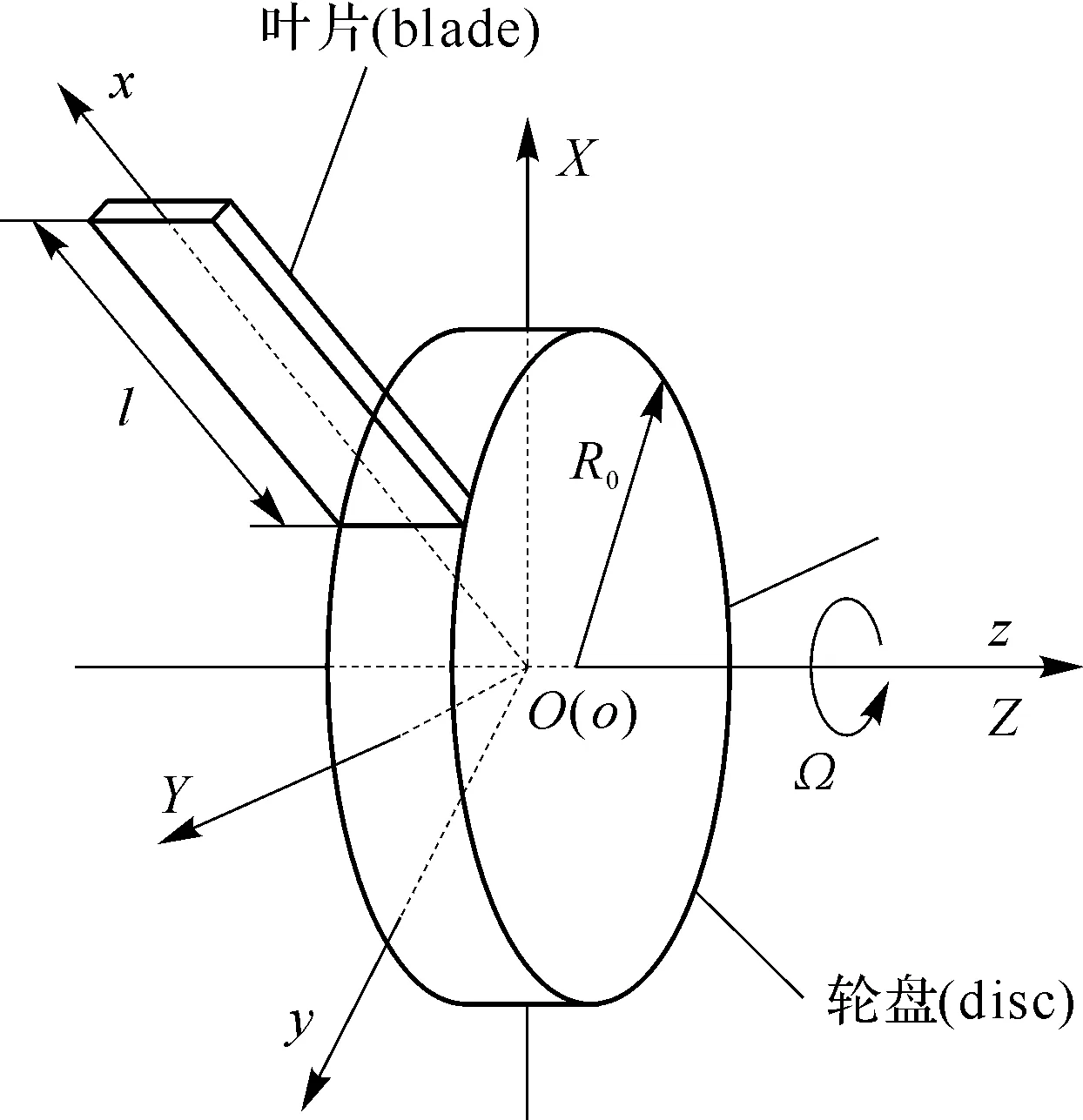
OXYZ为整体坐标系；O为轮盘中心和坐标原点；oxyz为叶片局部坐标系；局部坐标系原点o与整体坐标原点O重合；x轴与叶片中性轴重合；z轴与整体坐标系Z轴重合；轮盘绕Z轴以角速度Ω旋转；局部坐标系随叶片绕Z轴旋转；l为叶片长度，m；R0为叶片底部距离旋转中心的距离(即轮盘半径)，m。

叶片离心力受力分析见图16。

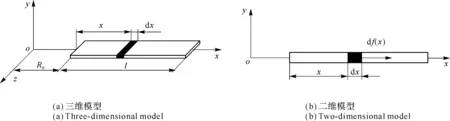
图16 叶片的离心力分析示意

沿径向方向距离叶片底端距离为x处的微元体dx旋转产生的离心力表现为如下形式。

df(x)=(ρAdx)Ω2(R0+x)=ρAΩ2(R0+x)dx

(28)

式中，df(x)为微元体dx所受到的离心力；ρ为叶片密度；A为叶片截面面积；Ω为叶片随轮盘绕Z轴旋转的角速度，rad/s。

微元段dx受到的总离心力

(29)

取微元段dx计算离心力在y向的分量(见图17)。

图17 离心力沿y轴方向的分量

可得

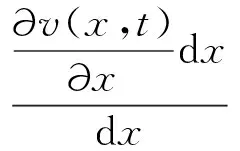
(30)

式中，v(x,t)为叶片的横向位移；θ为弯曲产生的微小摆角；v(x,t)为截面位置x和时间t的二元函数(为书写方便，下文以v代替)。

微元段dx的受力分析见图18。

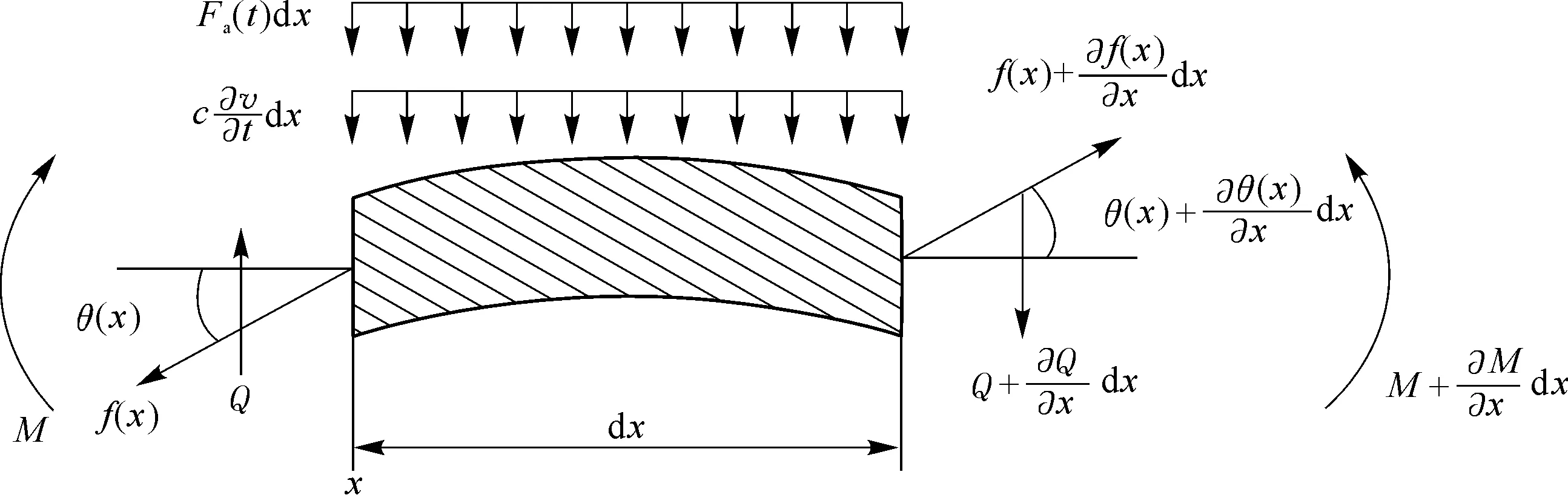
Q为横截面剪力；c为气动阻尼系数；f(x)为离心力产生的轴向载荷；Fa(t)为气动力；θ(x)为弯曲产生的微小摆角；M为叶片受到的弯矩。

根据力平衡原理，得到横向振动位移与各横向力之间的第一个关系式。

(31)

考虑微振动假设(见图17)，有

(32)

故式(31)可以改写为如下形式。

(33)

略去包含dx的二次项，式(33)可以简化为如下形式。

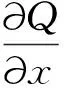
(34)

忽略截面转动的影响，微元段的转动方程可以表示为如下形式。

(35)

略去包含dx的二次项，式(35)可以简化为如下形式。

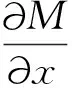
(36)

弯矩和梁的横向位移(可称为挠度(deflection))存在如下关系。

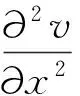
(37)

将式(36)和式(37)代入式(34)，经过整理，可以得到旋转悬臂弹性叶片的非线性动力学方程。

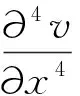
(38)

式中，f′(x)为离心力f(x)的导数。

考虑到气动阻尼相对于结构阻尼极小，忽略气动阻尼系数c后，式(38)可以改写为如下形式。

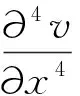
(39)

3.2.2 悬臂梁弯曲振动的模态函数

悬臂梁的模态函数(振型函数)可表述为如下形式[54]。

(40)

式中，φi(x)为悬臂梁第i阶模态函数；λi为第i阶特征值。

悬臂梁的频率方程——悬臂梁弯曲振动的特征方程，可以表述为如下形式。

cos(λi)cosh(λi)+1=0

(41)

由式(41)可求解得到前三阶特征值。

λ1=1.875 104 069λ2=4.694 091 133λ3=7.854 757 438

(42)

3.2.3 运动方程的离散

利用连续系统响应的振型叠加法(mode superposition method)，即把具有无限多个自由度的连续系统的位移表示成振型函数的级数，并利用振型函数的正交性(orthogonality)，将系统物理坐标的偏微分方程变换成一系列固有坐标的二阶常微分方程组[54]。这样，就可以按一系列单自由度系统问题来处理，还可以方便地得出系统对初始激励、外部激励或既有初始激励又有外部激励的响应。

根据振型叠加法，可将式(39)在给定悬臂边界条件的解v(x,t)变换为如下形式。

(43)

式中，qi(t)为正则坐标。

将式(43)代入式(39)，得

(44)

式(44)两边同时乘以φj(x)，并在区间(0,l)内积分，得

(45)

式中，φj(x)为悬臂梁的第j阶振型函数。

考虑到振型函数的正交性[54]，即

(46a)

(46b)

(46c)

对于无阻尼自由振动(non-damping free vibration)，其方程可以表示为如下形式。

(47)

其整体方程可表示为如下形式。

(48)

质量矩阵形式如下。

M=ρAldiag(1,1,…,1)n×n

(49)

刚度矩阵形式如下。

K=Ke+Kc

(50)

式中，Ke为弹性刚度矩阵(Elastic Stiffness Matrix，ELSM)；Kc为离心刚化效应产生的离心刚度矩阵(Centrifugal Stiffness Matrix，CSM)。

弹性刚度矩阵形式如下。

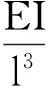
(51)

为了便于计算和书写，令

Kc=Kc1+Kc2

(52)

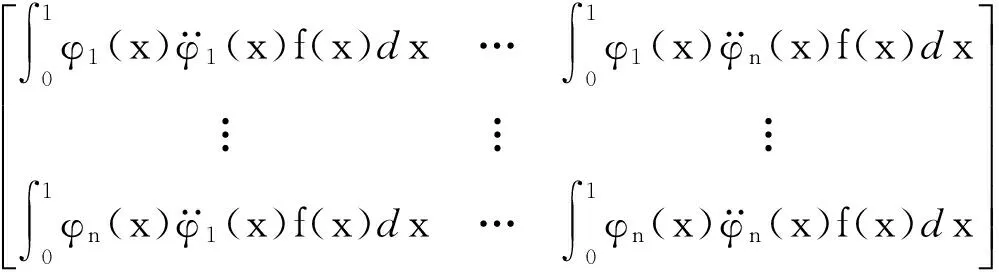
(53a)

(53b)

为了得到普适的离心刚度矩阵，对离心刚度矩阵进行无量纲化。令

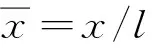
(54)

则有

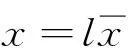
(55)

悬臂梁模态函数φi(x)及其一阶导数和二阶导数如下。

(56a)

(56b)

(56c)

将式(56)无量纲化，可得

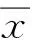
(57a)

(57b)

(57c)

对比式(56)和式(57)，可得有量纲模态函数及一阶导数、二阶导数与无量纲化模态函数之间的关系。

(58a)

(58b)

(58c)

对f(x)和f′(x)进行无量纲化，可以得到如下关系。

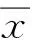
(59a)

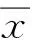
(59b)

将式(58)和式(59)代入离心刚度矩阵Kc1和Kc2，得

(60a)

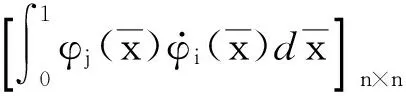
(60b)

为了方便计算和书写，将Kc1和Kc2中的部分算式定义为以下5个矩阵。

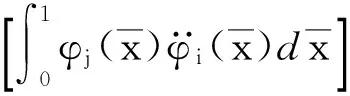
(61a)

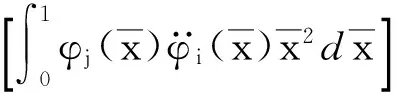
(61b)

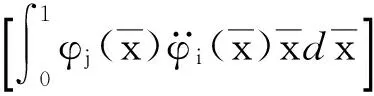
(61c)

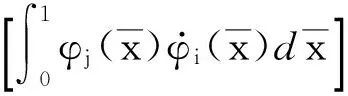
(61d)

(61e)

因为悬臂梁的模态函数已知，根据特征方程cosh(λi)cos(λi)+1=0，可以求出系统的n个特征值λi(i=1,2,…，n)；代入A1，A2，A3，A4，A5，可以得到5个常数矩阵。最终，离心刚度矩阵可表示为如下形式。

(62)

为了得到不同转速下的固有频率，需要通过求解行列式，获得固有频率解析表达式。

det(Ke+Kc1+Kc2-ω2M)=0

(63)

本文取n=3，即将前三阶模态函数φ1(x)、φ2(x)和φ3(x)代入质量矩阵M、刚度矩阵K及矩阵A1～A5。

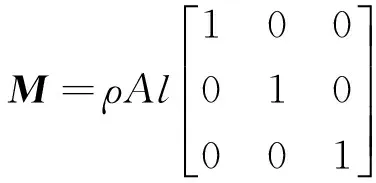
(64a)

(64b)

(65a)

(65b)

(65c)

(65d)

(65e)

将截断后求取的A1～A5代入离心刚度矩阵Kc，即可得到截断后的离心刚度矩阵。令

C*=-A1+A3+A4

(66a)

D*=(-A1+A2+2A5)/2

(66b)

计算矩阵元素值，得到如下结果。

(67a)

(67b)

考虑到C*和D*的对角线元素值对离心力产生刚度的贡献最大，而非对角元素相对于对角线元素而言很小，因此可以忽略非对角线元素的贡献。于是，式(63)可以改写为如下形式。

(68a)

进而可以表示为

(68b)

式(68b)中的ωi即为叶片旋转态下的动频率，由式(22)可得

(69a)

ωs=2πfs

(69b)

式中，ωs为叶片静频率,rad/s。

令

(70a)

ωd=ωi

(70b)

式中，ωr为转动频率，rad/s；ωd为叶片动频率，rad/s。

则动频率系数可表达为如下形式。

(71)

式(68b)表示为形如式(25)的动频率表达式。

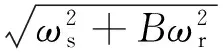
(72a)

即

(72b)

3.3 基于Euler-Bernoulli梁理论的有限元模型(EBB-FEM)的动频率分析

3.3.1 叶片有限元模型的建立

旋转态悬臂梁有限元模型见图19。

OXYZ为系统的整体坐标系；原点O位于轮盘中心；oxyz为局部坐标系，与整体坐标系OXYZ平行，原点o设置在叶片根部；R0为整体坐标系原点O与局部坐标系原点o之间的距离；l0为每个单元的长度；X轴和x轴与梁的中轴线重合；叶片-盘组合结构绕Z轴以转速Ω旋转。

基于Euler-Bernoulli梁单元理论(见图20和图21)对叶片进行单元离散。将叶片均匀划分为n个单元，叶片长度为l，则每个单元的长度为l0=(l/n)。离散化后的梁共n+1个节点，且每个单元具有2个节点(见图20)，略去x轴方向的位移，每个节点有沿y轴的平动位移(用ν表示)与绕z轴的转角位移(用θ表示)等 2个自由度。

图20 平面梁单元模型

图21 Euler-Bernoulli梁

假设梁的弯曲中心与其重心重合，则可忽略由于梁的弯曲而造成的弯扭耦合(coupled bending and torsion)。

点Pi为第i单元的任意一点(见图19)。在小变形条件下，有如下形式。

rPi=(i-1)l0+xi

(73)

式中，rPi为点Pi距局部坐标原点的距离；xi为点Pi距第i单元第1节点的距离。

【定义12单元节点位移向量(Element Nodal Displacement Vector，ENDV)qe】

(74)

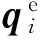
【定义13单元形函数(Element Shape Function，ESF)Ni(xi)】

(75)

式中，Ni(xi)为单元形函数；l0为单元长度。

则第i单元中的任意一点Pi的y方向位移

(76)

3.3.2 单元矩阵的推导

【定义14第i单元的单元应变能(Element Strain Energy，ESE)Ui[55]】

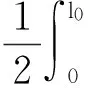
(77)

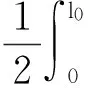
(77a)

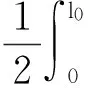
(77b)

式中，UiB为弯曲应变能；EI为抗弯刚度；UiF为离心力产生的应变能；FPi(xi)为离心力。

不同单元的离心力可表达为如下形式。

dFPi(xi)=ρAΩ2(R0+rPi)dxi

(78)

对式(78)从Pi点到梁的自由端进行积分，可以得到离心力

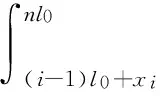
(79)

α2，α1，α0可以表达为如下形式。

(80a)

α1=2l0-2l0i-R0

(80b)

(80c)

单元应变能可以写成如下形式。

(81)

(82)

(83)

(84)

将式(84)代入式(83)，可得到EESM。

(85)

(86)

(87)

将式(87)代入式(86)，可得到ECSM。

(88)

【定义17第i单元单元动能(Element Kinetic Energy，EKE)Ti】

(89)

第i单元EKE可表示为如下形式。

(90)

(91)

将式(75)代入式(91)，可得到单元质量矩阵(EMM)。

(92)

对单元质量矩阵(EMM)和单元刚度矩阵(ESM)分别进行组集，形成整体质量矩阵(GlobalMassMatrix，GMM)M和整体刚度矩阵(Global Stiffness Matrix，GSM)K。

3.3.3 广义特征值问题

通过对整个梁所有单元的能量求和[56]，建立Lagrange函数。

(93)

由Lagrange函数构造Lagrange方程，可得

(94)

由Lagrange方程可得EBB-FEM的自由振动方程。

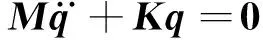
(95)

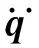
假设式(95)的解表现为如下形式。

(96)

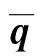
将式(96)代入式(95)可得到EBB-FEM的特征方程(characteristic equation)(即频率方程(frequency equation))

(97)

对式(97)求解，即可得到旋转态下EBB-FEM的固有频率和振型。

对于基于Timoshenko梁理论的有限元模型(TB-FEM)，本文通过悬臂梁实体建模再使用ANSYS进行分析的方法，采用Beam188单元进行模态分析。其中，Beam188单元是基于Timoshenko梁理论，包括剪切变形的影响，该单元有2个节点，每个节点有6～7个自由度。梁的边界条件为一端固支一端自由，模态求解方法采用Block Lanczos模态提取法，获得梁的前3阶弯曲模态对应的静频率。

3.4 叶片动频的数值算例

某叶片的几何尺寸和材料参数见表2[57]。

表2 叶片梁模型的几何尺寸以及材料参数

续表

3.4.1 基于3种模型静动频率的计算结果

采用3种模型得到的叶片的前3阶弯曲静频见表3。

表3 叶片的前3阶弯曲静频

从表3中可以看出，除了采用TB-FEM计算的2阶弯曲静频率与CB-AM和EBB-FEM的计算结果有约3 Hz的差别外，其他结果都比较相近。

取轮盘半径R0=l，使用matlab.针对CB-AM和EBB-FEM编写程序，同时使用ANSYS建立TB-FEM进行有限元分析，计算旋转态下叶片的前三阶弯曲固有频率，计算结果见图22。

图22 叶片前三阶弯曲动频曲线

从图22可以看到，CB-AM和TB-FEM计算的结果，在第1阶和第3阶计算结果几乎完全相同；TB-FEM的第2阶计算结果略小于CB-AM的结果，但动频率随转速增长的趋势完全一致；采用EBB-FEM的计算结果，在转速较低时与CB-AM差别很小，但随着转速的增加两者之间的差别逐渐增大，且EBB-FEM计算结果偏大。

对比3种计算模型，可以看出，叶片的动频率均随转速增加而增大，在转速较低时，三者差别较小，而随着转速的增加，采用EBB-FEM的计算结果偏大一些，但总体变化趋势3种基本相同，其中TB-FEM和CB-AM的结果符合很好。

3.4.2 基于3种模型的动频率系数计算

图23 不同模型得到的动频率、静频率和转频率关系曲线

从图23可以看到，3种计算模型计算结果均为直线(直线斜率即为动频率系数)，这表明动频系数为一定值；EBB-FEM的计算结果偏大一些，而采用CB-AM和TB-FEM的计算结果几乎完全符合。

当轮盘半径R0为0,l, 2l, 3l(l为叶片长度) 等4种情况时，用同样方法分别计算叶片前三阶弯曲固有频率的动频率系数，结果见表4。

表4 叶片前3阶弯曲动频率系数

从表4可以看出，对于同一阶动频率系数，R0不同的情况下得到的结果差别比较大，这是由于叶片旋转半径不同产生的离心力不同；对于相同的R0，TB-FEM与CB-AM得到的动频率系数比较相近，EBB-FEM得到的结果与TB-FEM和CB-AM有所差别。

3.4.3 动频率系数拟合公式与经验公式的对比

设置动频率系数[3]

(98)

式中，D为叶轮平均直径，本文近似认为D=2R0；α为一次项系数；β为常数系数。

以TB-FEM的计算结果为例，在R0=0,l, 2l, 3l等4种情况下动频率系数值，用来拟合动频系数的计算公式。对应地，可以设置自变量(D/l)向量为x。

(99)

动频率系数

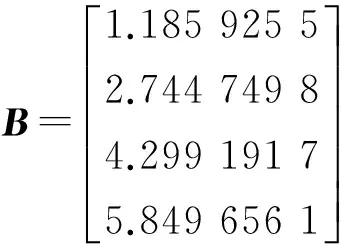
(100)

利用matlab.中的多项式拟合函数polyfit可得到如下的拟合公式。

B=0.777 3x+1.188 0

(101)

根据对应系数相等，可以确定α=0.777 3，β=1.188 0。依次类推，3种求解方法的动频率系数拟合公式系数见表5。

表5 动频率系数拟合公式的系数

对比3种模型的计算结果，可以发现基于TB-FEM和CB-AM的结果非常接近，而采用EBB-FEM的计算结果与二者差别稍大一些。

将动频率系数B的经验公式化为式(98)的形式，可得到经验公式中一次项系数α和常数项系数β的值(见表6)。

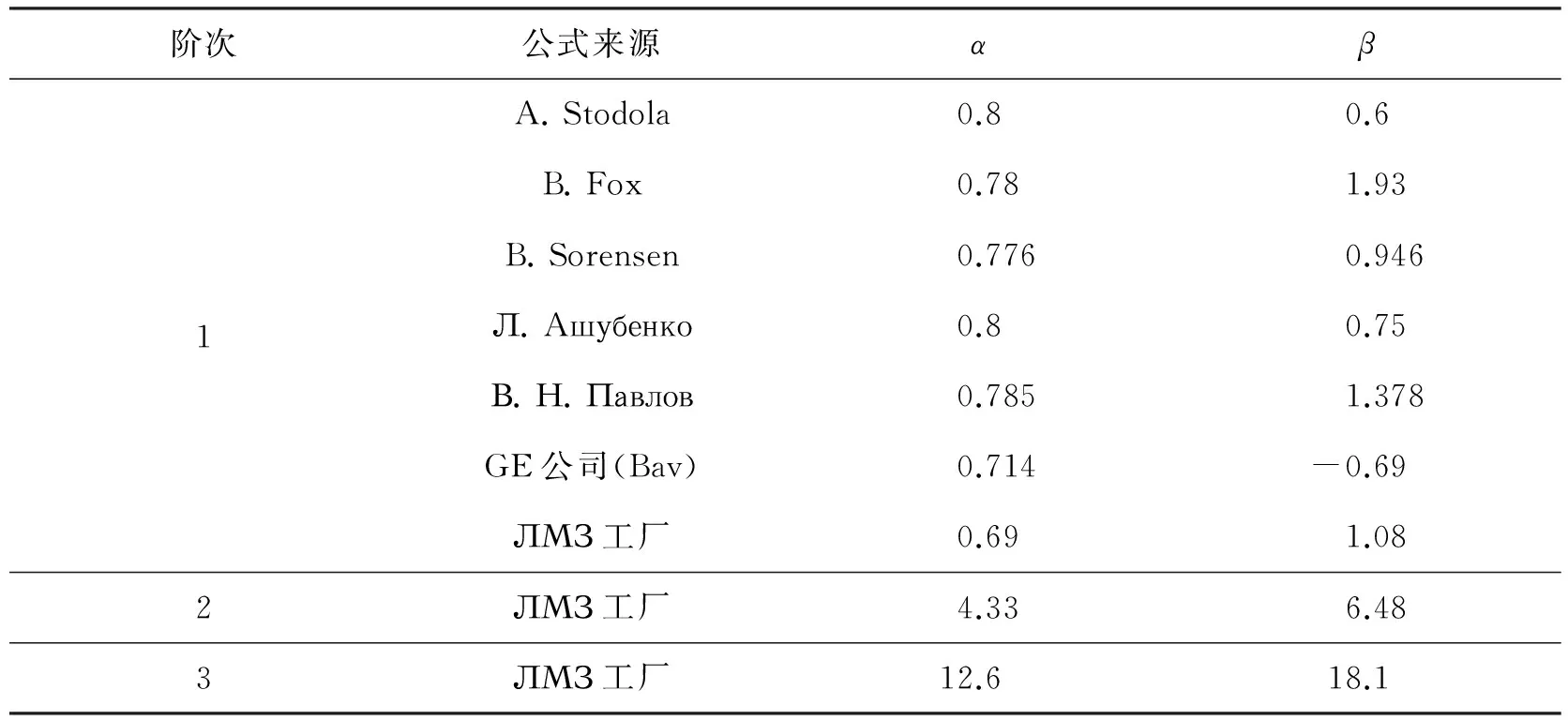
表6 动频系数经验公式中的系数

比较3种计算模型所得结果(见表5)和经验公式的结论(见表6)，可以看出：

(1) 根据已有文献，反映叶片一阶动频率的经验公式较多，比较可知仿真结果与经验公式结果的一次项系数基本相同，主要差别出现在常数项，而不同来源的经验公式常数项也存在较大差别；

(2) 根据已有文献，反映叶片二、三阶动频率的经验公式只有ЛМЗ工厂提供的一组，比较可知，仿真结果与经验公式结果的符合程度很好。

为了更加客观地评价每个动频率系数的公式，本研究团队认为不应单纯地比较动频率系数公式的一次项系数和常数项系数，而应该综合比较各种动频率公式所计算出的动频率系数对叶片动频值的影响。

图24为基于连续型解析模型(CB-AM)与基于各经验公式计算的叶片动频结果。在基于经验公式的计算中，叶片的静频率值采用通过式(21)的理论计算值，轮盘半径设为R0=l，转速变化范围为0～10 000 r/min，将各阶静频率、动频率系数和转速代入式(22)，计算叶片的动频。

从图24中可以清晰的看到，基于CB-AM的叶片二、三阶动频率的计算结果与ЛМЗ工厂提供的经验公式的结果符合得很好。而叶片一阶动频率的结果则因不同的经验公式差别较大，但除了B. Fox和GE公司(Bav)的公式外，基于CB-AM的计算结果与其余的结果都比较相近。

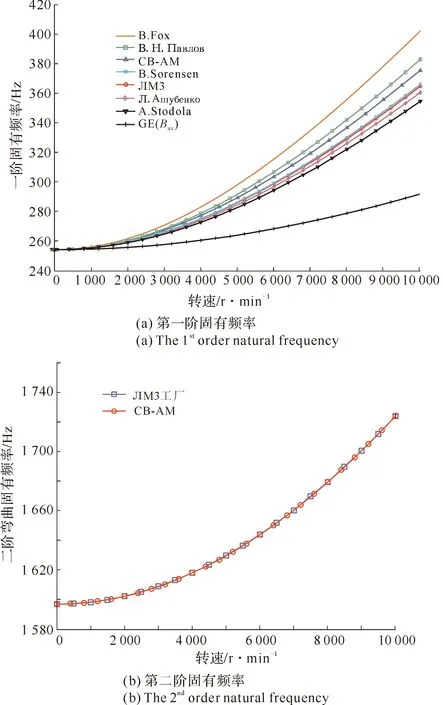
图24 叶片的前三阶弯曲动频率

4 叶尖与机匣的碰撞摩擦分析

当发动机稳定运转时，叶尖(blade tip)与机匣(casing)之间的接触以间歇性接触(intermittent contact)为典型特征。由于叶片模态自身的激发，或当机匣节径振动模态(nodal diameter mode)与叶片-盘组合结构(BD)的模态趋于一致时，都有可能会诱发很高的接触应力，导致叶尖断裂。为了提高发动机效率，采取减小叶尖与机匣间隙的措施，不可避免地增加了叶尖与机匣碰撞摩擦的几率，所以叶尖与机匣结构的碰摩研究[29]非常有必要。

4.1 叶片-盘组合结构(BD)与机匣的模态特征

BD与机匣均具有轴对称(axial symmetry)和圆周对称(cyclic symmetry)等特征，因此BD与机匣结构的模态振型(modal shape)如同其固有频率一样，均是成对出现的。以BD中的轮盘为例，对BD和机匣的模态特征进行描述。

对于静止态轮盘，由于其为一个连续弹性体，交变力作用点上的轮盘振动必然要向左右两个方向传播，这在轮盘振动中称为行波(traveling wave)，显然左右行波的行进速度是相同的。如果两行波相遇时的振动相位完全一致，就会产生物理学上的“驻波”(standing wave)，即机械振动中的共振现象。这时，轮盘周向在对称位置上出现振动节点，而且各半径上节点位置是相同的，这种振动被称为节径型振动(Nodal Diameter Vibration，NDV)。当静止轮盘作节径数为mnd的振动时，在整体坐标系中，两行波相对于轮盘以ω/mnd的速度向两侧传播(ω为此时轮盘振动的圆频率)。

对于旋转态的轮盘，行波的绝对速度应叠加上轮盘旋转的角速度Ω，此时两行波分别称为前行波(Forward Traveling Wave，FTW)和后行波(Backward Traveling Wave，BTW)。

【定义19前行波(FTW)】 顺着轮盘旋转方向转动的行波。

【定义20后行波(BTW)】 逆着轮盘旋转方向转动的行波。

在整体坐标系中，前行波的传播速度为Ω+ω/mnd，后行波的传播速度为Ω-ω/mnd。这使得旋转轮盘中两个行波的速度不再相等。

本研究团队将BD与机匣均看作弹性结构(elastic structure)，研究BD与机匣在具有相同节径数mnd的模态下振动接触碰摩问题。将BD与机匣的振型看作由正弦模态和余弦模态组成的节径数为mnd的模态。当发生振动时，其各自的振动位移的波动形式可以看作由正弦波和余弦波叠加后绕轴心沿着机匣轮廓(或叶片叶尖末端旋转圆周)传播，且振动能量在两结构发生相互接触时在彼此之间传递。

图25为3节径时机匣与叶尖之间发生接触碰摩的示意，点P为机匣上的任意一质点。当机匣与BD在节径数为3的模态下发生振动时，其时间历经过程见图25。从图25可以看到，两部件在振动过程中的变形可能会导致叶尖与机匣发生接触碰撞摩擦。

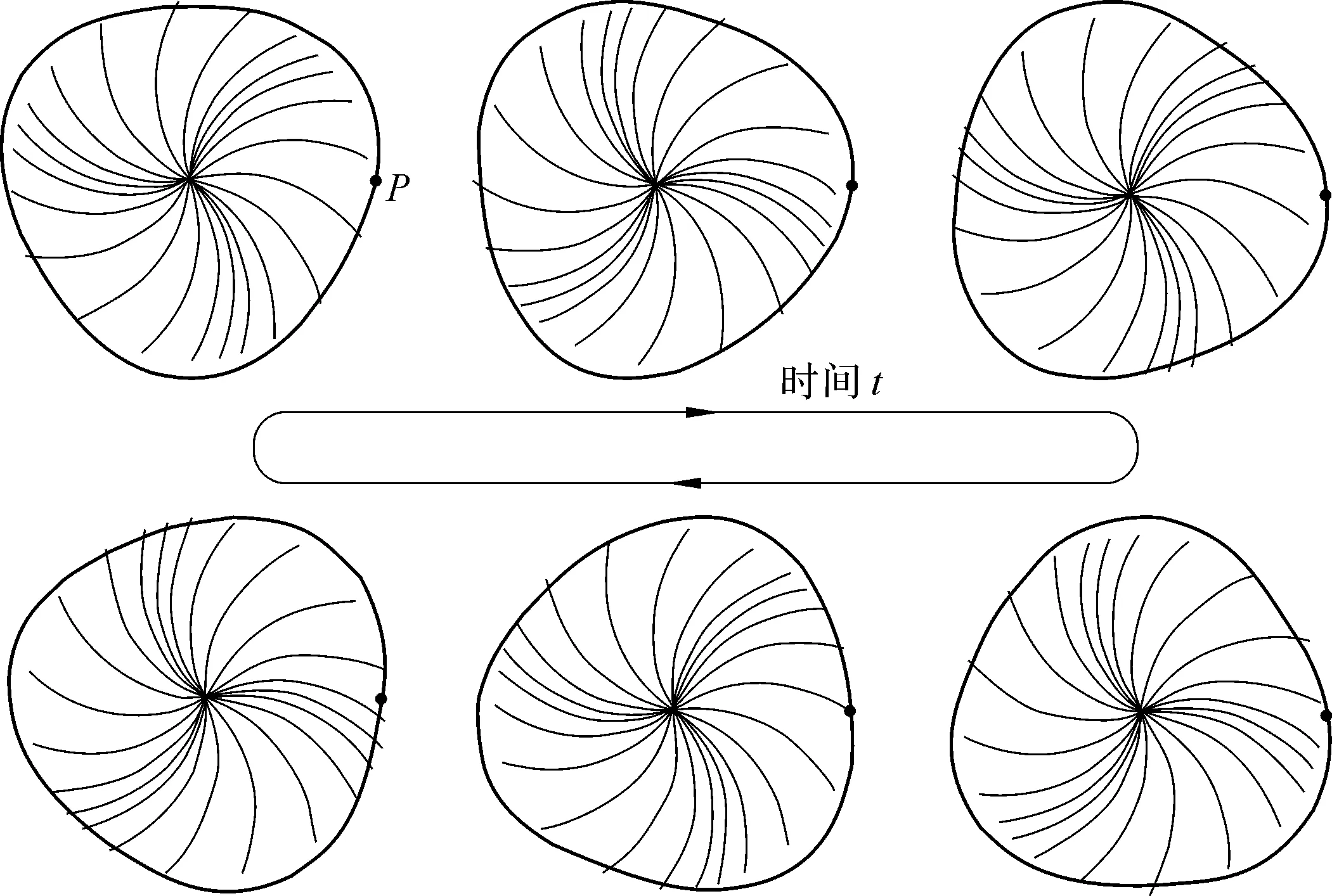
图25 节径数为3时BD与机匣接触碰摩的时间历程

本研究团队将BD与机匣分别离散简化为梁模型(beam model，BM)和质点模型(point-mass model，PMM)，在BD与机匣的节径数为3的模态振型下，计算其在各自振动时，叶尖与机匣之间间隙的变化规律。

4.2 叶片-盘组合结构与机匣的质点模型

4.2.1 叶片-盘组合结构的质点模型(Point-Mass Model of BD，BD-PMM)

为力求BD的结构模型简单，方便叶片与机匣的接触研究，提出如下假设[24]。

【假设1】 轮盘上安装有N个叶片，每一个经调谐装配好的叶片均为刚体，通过刚度为kb的线性弹簧连接于轮盘上，相邻叶片之间通过刚度为kbb的线性弹簧连接(见图26)。

【假设2】 简化后的叶片振动只发生在发动机旋转方向上，也就是说认为BD的径向振动位移为零。

【假设3】 忽略离心力、科氏力和陀螺效应的影响。

图26 叶片-盘组合结构(BD)示意

以轮盘的圆心为原点，轴向为Z轴，建立整体坐标系OXYZ(见图26)。

根据图26，对第i个叶片受力分析，由牛顿第二定律(Newton’s Second Law of Motion)，可得

(102)

式(102)可表示为如下形式。

(103)

考虑整体结构，则运动方程可表示为如下形式。

(104)

式中，Mbd为整体质量矩阵；Kbd为整体刚度矩阵；Fbd为叶片受到的外力矩阵。

整体刚度矩阵可以表达为如下形式。

Mbd=diagN(mb)

(105)

式中，N为叶片个数。

记k1=kb+2kbb，k2=-kbb，则整体刚度矩阵为循环刚度矩阵(Circulant Stiffness Matrix，CSM)，其形式如下。

Kbd=circN(k1,k2,0,…,0,k2)

(106a)

即

(106b)

叶片振动在整体坐标系下的角位移向量

α=[α1…αN]T

(107)

【假设4】 叶片叶尖处的振动模态由余弦和正弦模态组成。

根据“假设4”，叶片在整体坐标系OXYZ中的角位移与其模态坐标Pb之间的关系如下。

(108)

(109a)

(109b)

φi=2πi/N(i=1,2，…，N)

(109c)

式中，αc为叶片在模态坐标中角位移的余弦分量；αs为叶片在模态坐标中角位移的正弦分量；Pb为模态坐标；Pbc为模态坐标的余弦分量；Pbs为模态坐标的正弦分量；Abd为振动的幅值；mnd为节径数；φi为第i个叶片的初始角，i=1,2，…，N。

模态质量矩阵(Modal Mass Matrix，MMM)可以表现为如下形式。

(110a)

模态刚度矩阵(Modal Stiffness Matrix，MSM)可以表现为如下形式。

(110b)

模态力向量(Modal Force Vector，MFV)可以表现为如下形式。

(110c)

若叶片的个数为N=22，均匀分布在轮盘上。t=0时刻，第i个叶片自由状态时叶尖在整体坐标系OXYZ中的坐标可以表现为如下形式。

(111)

式中，Xti(t)为第i个叶片叶尖在整体坐标系OXYZ中的X坐标；Yti(t)为第i个叶片叶尖在整体坐标系OXYZ中的Y坐标值；l为叶片长度；R0为轮盘半径。

当叶片随叶盘以Ω的角速度绕盘轴旋转时，经过时间t后，每个叶片相应转过的角度β=Ωt。则叶片在整体坐标系下的角位移

(112)

考虑到在叶片发生振动后，其振动角位移为αi，此时叶尖处在整体坐标系OXYZ中坐标如下。

(113)

由叶片的角位移在整体坐标系OXYZ与其模态坐标之间的变换关系，可得余弦模态在整体坐标系OXYZ中的坐标。

(114a)

正弦模态在整体坐标系OXYZ中的坐标可以表述为如下形式。

(114b)

BD的余弦模态分量和正弦模态分量在BD节径数为3的模态中的贡献见图27。

图27 机匣和叶片-盘组合结构节径数为3的模态振型

4.3.2 机匣的质点模型(Point-Mass Model of Casing, C-PMM)

将机匣看作由围绕着机匣所在圆周的Nc个质点组成，整体坐标系OXYZ与BD的整体坐标系相同(见图28)。

图28 机匣质点模型

机匣自由静止状态时，第j个质点在OXYZ整体坐标系中的坐标值

(115)

式中，Rc为机匣的半径；θj为机匣离散后，以OX轴为起始位置的第j个质点的角位置。

第j个质点的角位置

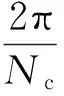
(116)

式中，Nc为机匣所在圆周质点的个数。

在模态坐标系中，每个质点的mnd节径模态位移

(117)

式中，Ac为振动幅值；θ0为初始相位角；uc为模态坐标变量的余弦分量；us为模态坐标变量的正弦分量。

令

u=[ucus]T=[cosωtsinωt]T

(118)

式中，u为模态坐标变量。

于是，可以得出机匣在发生振动后，第j个质点在整体坐标系OXYZ中的坐标如下。

(119)

将式(119)展开，可得

(120a)

(120b)

由式(120)可以推导出机匣每个质点的模态位移与整体坐标系下位移的关系。

(121)

按照式(121)，可以得出机匣的余弦模态在整体坐标系OXYZ中的坐标方程，以及机匣的正弦模态在整体坐标系OXYZ中的坐标方程。

(122a)

(122b)

令

(123)

式中，Pc为机匣每个质点的模态坐标与整体坐标之间的坐标变换矩阵。

若将机匣直接在模态坐标系下离散，其余弦分量和正弦分量在3节径模态中的贡献见图27。

机匣的振动方程可以表示为如下形式。

(124a)

Mc=diag2(mc)

(124b)

Kc=diag2(kc)

(124c)

4.3.3 叶尖与机匣的系统动力学方程

叶尖与机匣的接触属强非线性动力学问题，若考虑机匣与叶尖之间的相互接触作用，其动力学方程的求解将非常困难[24-25，30]。本研究团队在不考虑摩擦影响的前提下，分析机匣与叶尖之间的接触间隙。

基于变分原理，根据Hamilton定理，建立机匣和叶尖的统一方程。Hamilton变分原理可表示为如下形式。

(125)

∀(δu,δα)，有

δu|t1=δu|t2=δα|t1=δα|t2=0

(126)

式(125)所涉及的动能、势能与虚功的表达形式如下。

(127a)

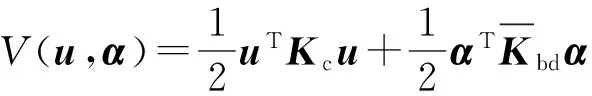
(127b)

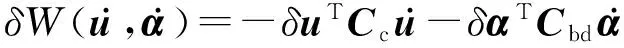
(127c)

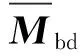
为了协调以上方程，提出Cc和Cbd的表达形式。

Cc=diag2(cc)

(128a)

Cbd=diag2(cbd)

(128b)

cc=2ωcζc

(128c)

cbd=2ωbdζbd

(128d)

式中，cc为机匣的阻尼系数；cbd为BD的阻尼系数；ωc为机匣的m节径模态下的固有频率；ωbd为BD的m节径模态下的固有频率；ζc为机匣的阻尼比；ζbd为BD的阻尼比。

将式(127)和式(128)带入式(125)，可得

(129a)

∀(δu,δα,δλ)，有δu|t1=δu|t2=δα|t1=δα|t2=0

(129b)

可得BD与机匣整体系统的运动微分方程。

(130)

式(130)中的质量矩阵、阻尼矩阵和刚度矩阵可表示为如下形式。

(131a)

(131b)

(131c)

xT=[uT,αT]

(131d)

对式(130)采用中心差分法(central difference method)在时间上离散，则速度和加速度向量可以离散化为如下形式。

(132a)

(132b)

式中，xn-1为第n-1步的速度值；xn为第n步的速度值；xn+1为第n+1步的速度值；h为积分步长。

中心差分法是一种显式积分方法，在计算时并非是无条件稳定的，其积分时间步长h不能大于临界值Δtcr，即

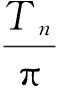
(133a)

(133b)

式中，Tn为离散系统的最小周期；ωmax为离散系统的最大固有频率。

4.3.4 数值算例

由于叶尖与机匣之间的间隙直接影响着叶尖与机匣的接触碰撞特性，因而需要讨论叶尖与机匣之间间隙的变化规律。

4.3.4.1 间隙函数

图29为第i个叶片与机匣之间的间隙示意。

图29 第i个叶片与机匣之间的间隙示意

(134a)

(134b)

lb=R0+l

(134c)

4.3.4.2 接触间隙计算步骤

本研究团队结合中心差分法计算叶尖与机匣之间的接触间隙。计算步骤如下。

【程序1初始计算】

[step1] 组构质量矩阵M，阻尼矩阵C和刚度矩阵K。

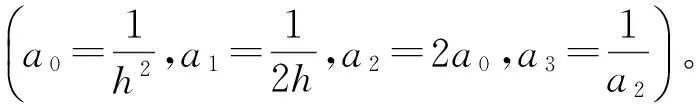
【程序2时间增量计算】

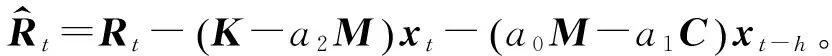
[step3] 计算机匣与叶尖之间的间隙函数值，储存在N×1向量g中，若间隙函数值为负，则意味着机匣与叶尖之间有侵入量。

[step4] 增加时间步长。

4.3.4.3 数值计算结果

【计算案例】 给定轮盘转速Ω=10 rad/s；在机匣的uc方向上施加一个周期变化的脉冲载荷以激发机匣发生振动；对每个叶片均施加周期气流激振力；不考虑转子的不平衡、不对中，以及轮盘的偏心等因素的影响。给定一组系统模型的物理参数及几何参数(见表7)，计算叶尖与机匣之间的间隙。

表7 模型的物理参数与几何参数

按照“接触间隙计算步骤”，分别计算具有22个叶片的叶盘与机匣之间的2节径模态的接触间隙，计算结果见图30和图31。

图30 余弦模态下叶尖与机匣之间的间隙

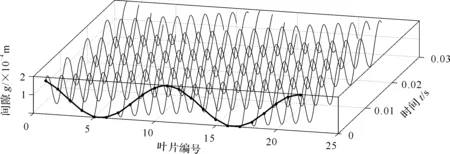
图31 余弦与正弦模态共同作用下叶尖与机匣之间的间隙

图30为叶盘上22个叶片在余弦模态下计算的与机匣之间的间隙结果。可以看出叶盘上不同叶片与机匣之间的间隙的变化规律并不相同，而且22个叶片的间隙波动也是由两个完整波绕叶盘转动的圆周传播。

图31为计算得到的BD在余弦与正弦模态共同作用下，叶尖与机匣之间的间隙变化结果。图31反映出在正弦与余弦模态共同作用下，轮盘上各个叶片与机匣之间的间隙变化规律基本一致，但初始相位并不相同，且仍可反映出间隙的波动波形为两个完整波。

图32给出了第1、4、9号叶片的间隙计算结果，从中可以清晰地看到，叶尖与机匣之间的间隙随着时间的变化呈现出规律性的变化。叶尖与机匣之间的间隙值在初始间隙值(0.1 mm)附近波动，当间隙值为负值时，说明叶尖与机匣已发生接触。图32中还可以看出BD在2节径模态下行波的波速传播方向v。

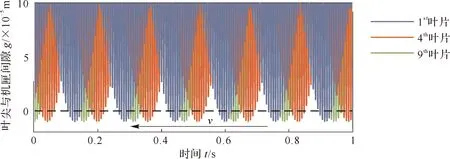
图32 第1，4，9号叶片叶尖与机匣之间的间隙变化

4.4 叶片-盘组合结构梁模型(BD-BM)与机匣梁模型(C-BM)

由于BD-PMM与C-PMM的自由度少，建立的动力学方程相对简单，BD-PMM与C-PMM的精确度或是逼近实际工况的程度均有不足。如果分别对BD与外部机匣进行直梁与曲梁模型的有限元离散，可以更加精确地研究BD与机匣的动力学特性。故而本研究团队拟在叶片-盘组合结构梁模型(Beam Model of BD，BD-BM)和机匣梁模型(Beam Model of Casing，C-BM)等方面做出探索。

4.4.1 建立模型

如图33所示，将机匣与BD的每个扇区分别离散为Nc段曲梁(curved beam)和Nbd个Euler-Bernoulli直梁(straight beam)。将简化后的轮盘中的每一段直梁单元均看作刚体，整体坐标系固定在转子的轴心位置[29]。

轮盘安装N个叶片；每个叶片的初始相角φi=(i-1)2π/N；叶片每段直梁的长度lbd=Lbd/Nbd(Lbd为叶片到轴心的总长)；每个叶片中，第k段直梁相对于第k-1段直梁的夹角为αk，它决定着相邻两直梁之间的相对位置关系。

将机匣离散为Nc段曲梁，则每段曲梁的长度lc=2πRc/Nc(Rc为机匣半径)。

叶片经离散后，在局部坐标系中，直梁单元的每一个节点具有ubl，vbl和γbl等3个自由度(见图33)。

图33 叶片-盘组合结构与机匣的梁模型

第k段直梁单元在vbl方向上的位移

(135)

式中，Nv(x)为梁单元的局部形函数；δe为节点位移向量。

局部形函数Nv(x)可以表述为如下形式。

(136a)

(136b)

(137a)

(137b)

ubl方向上的位移可以表述为如下形式。

(138)

其局部形函数可以表述为如下形式。

(139a)

(139b)

如同上述表述，可以将经离散后的机匣的第j个曲梁单元的位移场表述为如下形式。

(140a)

(140b)

式中，s为沿曲梁弧长方向的坐标。

4.4.2 叶片-盘组合结构与机匣梁模型的计算案例

假设N=22，Nc=44，基于matlab.平台进行仿真计算，同时采用实体建模后进行ANSYS有限元分析，得到BD的节径数为0～4的模态振型(见图34)，得到机匣节径数为1～4的模态振型(见图35)。

从图34可以看出，BD的节径模态特征是，1节径出现1个波峰1个波谷；2节径出现2个波峰2个波谷；3节径模态出现3个波峰3个波谷，依次类推。

从图34中还可以看出，每个节径下的模态对称轴。对比matlab.与ANSYS的计算结果，验证了叶片-盘组合结构梁模型(BD-BM)的可适用性，对BD这种轴对称和循环对称结构的节径模态概念的理解也更加清晰。

图34 叶片-盘组合结构节径数为0～4的模态振型

从图35可以看出，机匣梁模型(C-BM)与使用ANSYS进行有限元分析得到了相同的结果，这证明本研究团队建立的C-BM具有可适用性。

从图35还可以看出，由于机匣属于类似BD的轴循环对称结构，因此具有与BD类似的节径模态特征——1节径出现1个波峰1个波谷，2节径模态出现2个波峰2个波谷，依次类推。

需要指出的是，本研究团队虽然初步建立了BD-BM和C-BM，但未给出单元质量矩阵和刚度矩阵的详细表达式，没有采用BD-BM和C-BM对叶尖与机匣之间的碰撞摩擦特性进行分析，这部分工作还有待于进行。另外，由于机匣与叶片-盘组合结构梁模型的总体自由度过大，这对实际计算不利，故而需要对计算方法展开更深入的研究。

图35 机匣1～4节径的模态振型

5 考虑接触摩擦特性下叶片-轮盘组合结构(BD)的振动特性

叶片的动力学特性很大程度上受到轮盘刚度的影响，尤其当轮盘刚度较弱的情况下影响更大；反过来，轮盘的振动特性也同样受到叶片的影响。叶片与轮盘之间的互相影响，不仅改变了频率的数值，而且还改变了固有频率的阶数。近年来，随着涡轮技术的发展和计算机技术的应用，在围绕涡轮机转子叶片气动弹性研究中，许多学者进行了叶片-轮盘组合结构(BD)的振动分析。由于叶片和轮盘的几何形状复杂，载荷比较复杂[58]，使得BD的振动成为一个比较复杂的问题。

长期以来，航空发动机叶片与轮盘系统的动力学设计与分析，一直是将叶片和轮盘作为单独元件进行动力学设计，或者是将叶片与轮盘当成一个整体进行动力学设计，没有考虑到叶片与轮盘之间的装配结构及其配合关系，从而导致叶片和轮盘的预测频率失真，造成设计参数选择不佳[34]。

本研究团队在进行BD振动分析时，将叶片与轮盘当作一个具有接触摩擦特性(Contact Friction Characteristics，CFC)的动力耦合系统(dynamic coupling system)，在带有CFC的情况下，研究BD的整体振动特性。为此，本研究团队提出了考虑CFC的情况下BD的固有特性有限元计算分析方法，并对比分析了叶片榫头与轮盘榫槽在固支边界条件下和带有CFC的边界条件下对固有特性的影响，绘制出各自的Campbell图。

5.1 BD振动模式

BD振动是在轮盘和叶片刚性基本相近条件下形成的整体振动，有其特定的动力学特性。为了更好地描述BD的振动形式，本研究团队将BD振动模式分别用轮盘振动、叶片振动，以及BD整体振动(即叶片与轮盘之间的振动耦合形式)来描述。BD整体振动模式与轮盘振动类似。

轮盘振动包括节圆振动(Nodal Circle Vibration，NCV)和节径振动(Nodal Diameter Vibration，NDV)等两种基本振型。轮盘高阶振型均为这两种基本振型的复合。

【定义21节圆振动(NCV)】 在节圆上，各点静止不动，在节圆内外两侧各质点作相位相反的振动，同一半径圆上各质点振动幅值和相位相同。

若用nd表示轮盘的节圆数，nbd表示BD的节圆数。轮盘节圆数为1～3的节圆振动示意见图36。

图36 轮盘的节圆模态

对于BD的节圆振动，节圆有时会跑出轮盘，而存在于叶片处(见图37)。特别是带有长叶片的轮盘，极有可能产生这种情况[58]。

图37 节圆位于叶片处的BD的节圆振动(nbd=1，nd=0)

【定义22节径振动(NDV)】 具有一个或几个直径节线的振动。

虽然节圆振动(NCV)和节径振动(NDV)等两种振型都可能发生，但BD结构共振引起的种种破坏，绝大部分为NDV所产生[58]。用mbd表示BD的振型中的节径数，用md表示轮盘的振型中的节径数。

图38 轮盘的节径模态

发动机中的气体激振力(FIF)可以通过叶片传递到BD，机械激振力(Mechanical Excitation Force，MEF)也可以通过轴承等中介结构传递到BD。此外，稳定流中的畸变力(Distortion Force，DF)、均匀流中的自激振动(Self-Excited Vibration，SEV)也都能通过叶片传递到BD。这些因素都可能激发BD振动。BD的共振条件为[59]：BD的固有频率必须与激振频率相等；激振力的谐波数K必须与BD振动时的节径数mbd相等，即K=mbd。

在叶片振型中，用mb表征沿叶片长度方向(图中x方向)上的半波数，nb表征沿叶片宽度方向y上的半波数(见图39)。

图39 叶片的振型

5.2 BD有限元分析

5.2.1 有限元模型

设置整体坐标系(见图40)为：X向为BD的径向，Y向为周向，Z向为轴向。

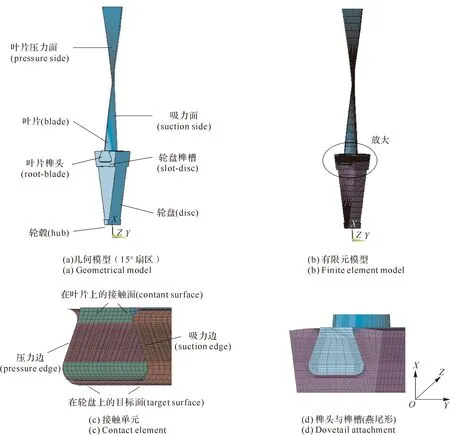
图40 叶片-盘组合结构有限元模型

图40(a)为BD的一个15°扇区。采用ANSYS中的ICEM模块对BD的结构实体模型进行网格划分，得到其六面体网格(见图40(b))。

在该模型中，两部分实体均选择Solid185单元，材料均为钛合金Ti-6A-4V[60]，其弹性模量E=110 GPa，泊松比为0.3，密度ρ=4 500 kg/m3。

在实际工作中，轮盘装配在旋转轴上进行旋转运动，因而对BD进行轴向和周向的固定约束，只允许其在径向有较小的位移。关于叶根榫头与轮盘榫槽之间的关系，分别采用以下两种方式进行分析。

(1) 固支边界条件 在叶片榫头两侧与轮盘榫槽之间的接触面进行节点自由度耦合，即将叶片与轮盘视为刚性连接。

(2) 带有CFC 在叶片榫头和轮盘榫槽之间可能会产生接触的表面上分别添加三维8节点的面-面接触单元CONTA174和三维目标单元TARGE170。其中，摩擦系数设置为0.3，接触刚度的默认值设置为1.0，创建非对称接触对(Asymmetric Contact Pair)。最终创建的接触对见图40(c)。

BD的主要载荷为轮盘和叶片由于转动而产生的离心力。对BD分别施加2 500 r/min，5 000 r/min，7 500 r/min和10 000 r/min等4种转速，求解不同转速下的BD的固有频率。

在计算过程中，施加循环对称边界条件，使其成为一个完整结构，能够更好地模拟BD的实际工作过程，使计算更加接近实际工况。对基本扇区进行循环扩展(cyclic expansion)，扩展后BD有限元模型中网格节点数为56 968，单元数为53 528，其中接触单元5 232个，接触区节点数为5 664个，接触区的压力边(吸力边)长度为12 mm。

5.3 结果分析

5.3.1 固有特性分析

对于BD的固有特性分析的主要流程见图41，分别计算BD在节径数mbd=0～10时的固有特性和振型。

图41 叶片-盘组合结构模态分析的求解过程

取某种转速下考虑CFC与叶片视为固支的情况下得到的固有频率和振型，观察CFC对BD固有特性的影响。表8为BD转速为10 000 r/min，节径数mbd=0，对应地，考虑CFC和不考虑CFC的固有频率和振型。

表8 节径数mbd=0对应的叶片-盘组合结构的固有特性

如表8和图42所示，以考虑接触摩擦特性的振型图为例，通过观察ANSYS中的动态图来对比说明考虑接触摩擦特性和不考虑接触摩擦特性的叶片-盘组合结构模态振型的特点。

(1) 当轮盘不发生振动(即BD的mbd=0，nbd=0和轮盘的md=0，nd=0时)，BD的振型图表现为叶片的振型。其中考虑接触摩擦特性和未考虑接触摩擦特性的振型图相符(见图42(a1)和图42(b1)，图42(a2)和图42(b2)，图42(a3)和图42(b3)，图42(a6)和图42(b5)，图42(a10)和图42(b9))。

(2) 当轮盘发生节圆振动(即BD的mbd=0，nbd=2时)，轮盘的振动可导致叶片发生复合振动。其中考虑接触摩擦特性和未考虑接触摩擦特性的振型图不相符(见图42(a8)和图42(b7)，图42(a9)和图42(b8))。图42(a8)，图42(b7)和图42(a9)是叶片的复合振动，图42b(8)是叶片的弯曲振动。对于BD结构的节圆振动，节圆有时会跑出轮盘，而存在于叶片处。特别是像具有长叶片的轮盘，极有可能产生这种情况。研究表明，伞形振动和具有节圆的振动只有在叶轮刚性不足的情况下才会发生。当轮盘较大、叶片较长、轮盘比较薄时，才可能发生节圆振动。具有节圆和节径的复合振动则更为少见。

考虑接触摩擦特性与不考虑接触摩擦特性的固有频率具有如下特点。

(1) 在BD振型图相符情况下对应的固有频率，不考虑接触摩擦特性的BD结构的固有频率要比考虑接触摩擦特性的固有频率高。图42(a1)和图42(b1)、图42(a2)和图42(b2)、图42(a3)和图42(b3)、图42(a6)和图42(b5)、图42(a10)和图42(b9)振型图对应的固有频率差值分别为13.14 Hz，11.07 Hz，68.71 Hz，11.73 Hz和8.19 Hz。

(2) 在BD振型图不相符情况下对应的固有频率，其中考虑接触摩擦特性的BD中(见图42(a5))振型对应的固有频率在不考虑接触摩擦特性中没有对应的振型存在，即没有相应的固有频率。图42(a4)和图42(b4)、图42(a7)和图42(b6)、图42(a8)和图42(b7)、图42(a9)和图42(b8)振型图对应的固有频率差值分别为160.96 Hz，-87.68 Hz，107.11 Hz和16.21 Hz。

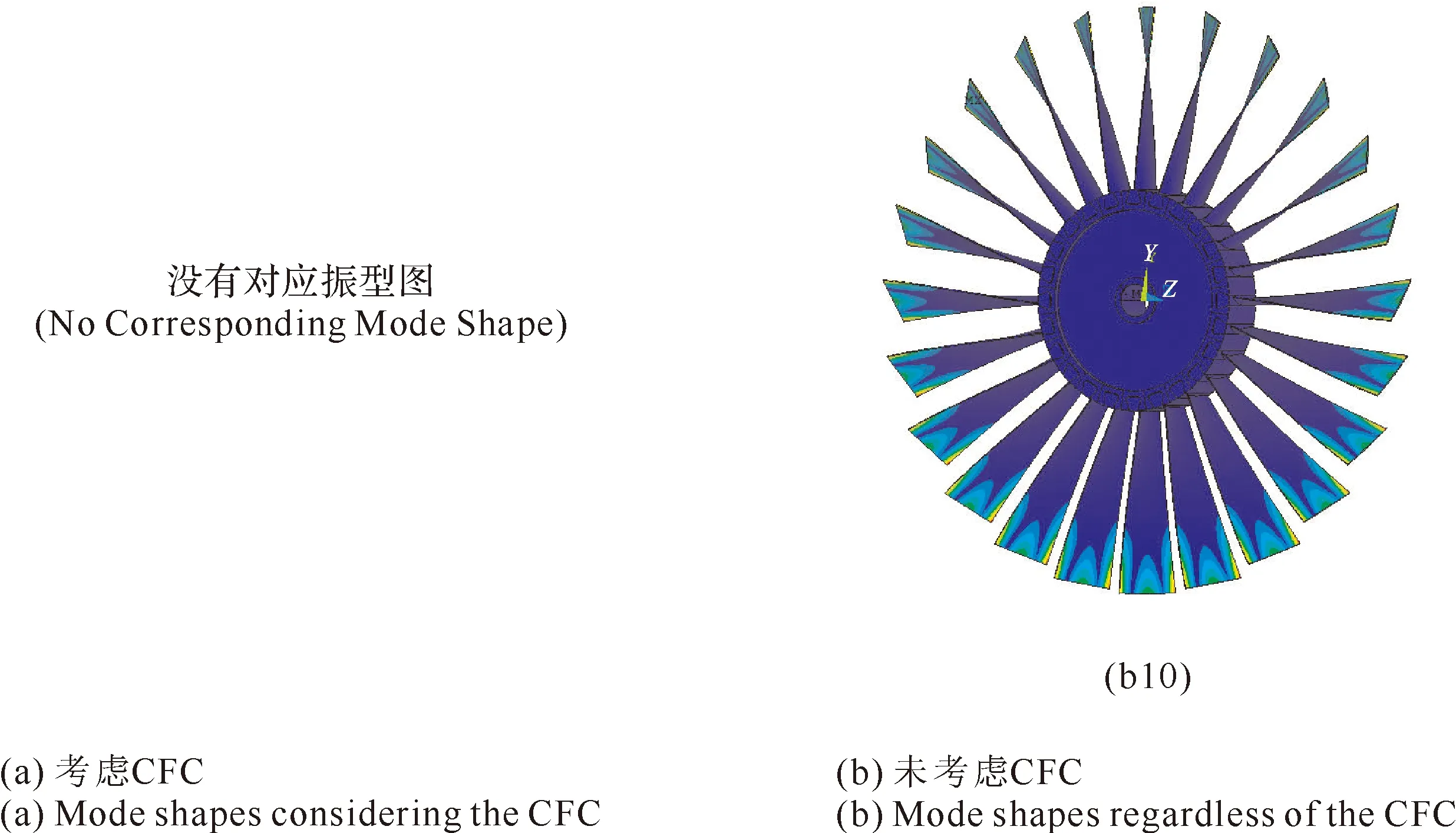
图42 节径数mbd=0对应的叶片-盘组合结构振型

当BD呈现节径振动时，由于组合结构的对称性，在非0节径下每一阶均有两个相同的固有频率出现，相对应的振型呈现正交形式。因此，文中只列出了相同频率下的一组振型，正交形式的振型未一一列出。

表9为BD转速在10 000 r/min，节径数mbd=4时，对应地考虑CFC与不考虑CFC的BD的固有频率和振型图。由表9，考虑CFC与未考虑CFC时BD的固有频率有所差异，其中最大差值为127.57 Hz，最小差值为7.13 Hz。考虑CFC与未考虑CFC的模态振型比较相符(见图43)。

其他节径数对应的BD的模态振型与节径数mbd=4时特点相似，BD的振型都主要表现为叶片的振动。这说明，BD在低节径振动时，轮盘对叶片的振动影响较大，随着节径数的增大，轮盘对叶片的振动影响逐渐减小，更多的表现为叶片的振动形式。

对比节径数mbd=0和mbd=4时BD的固有频率可以看出，节径数mbd=4对应的固有频率大于节径数mbd=0对应的固有频率，说明BD的固有频率随着节径数的增加而增大。

表9 节径数mbd=4对应的叶片-盘组合结构的固有特性

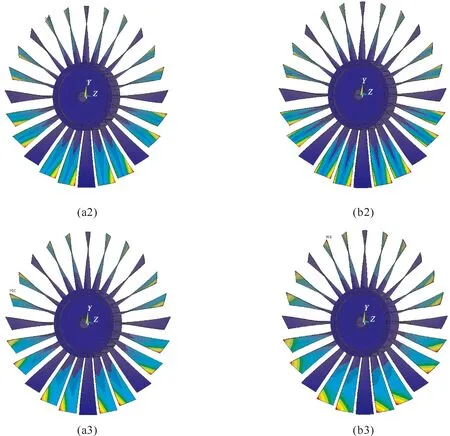
图43 节径数mbd=4对应的叶片-盘组合结构振型

5.3.2 共振分析

对于建立的BD有限元模型，在前述4种转速下，分别分析BD在考虑CFC和未考虑CFC，节径数mbd=0～10时的第1阶固有频率(即叶片发生1阶弯曲振动，轮盘不振动)，绘制Campbell图。图 44为考虑CFC时，BD振动的Campbell图，图45为未考虑CFC时，BD振动的Campbell图。

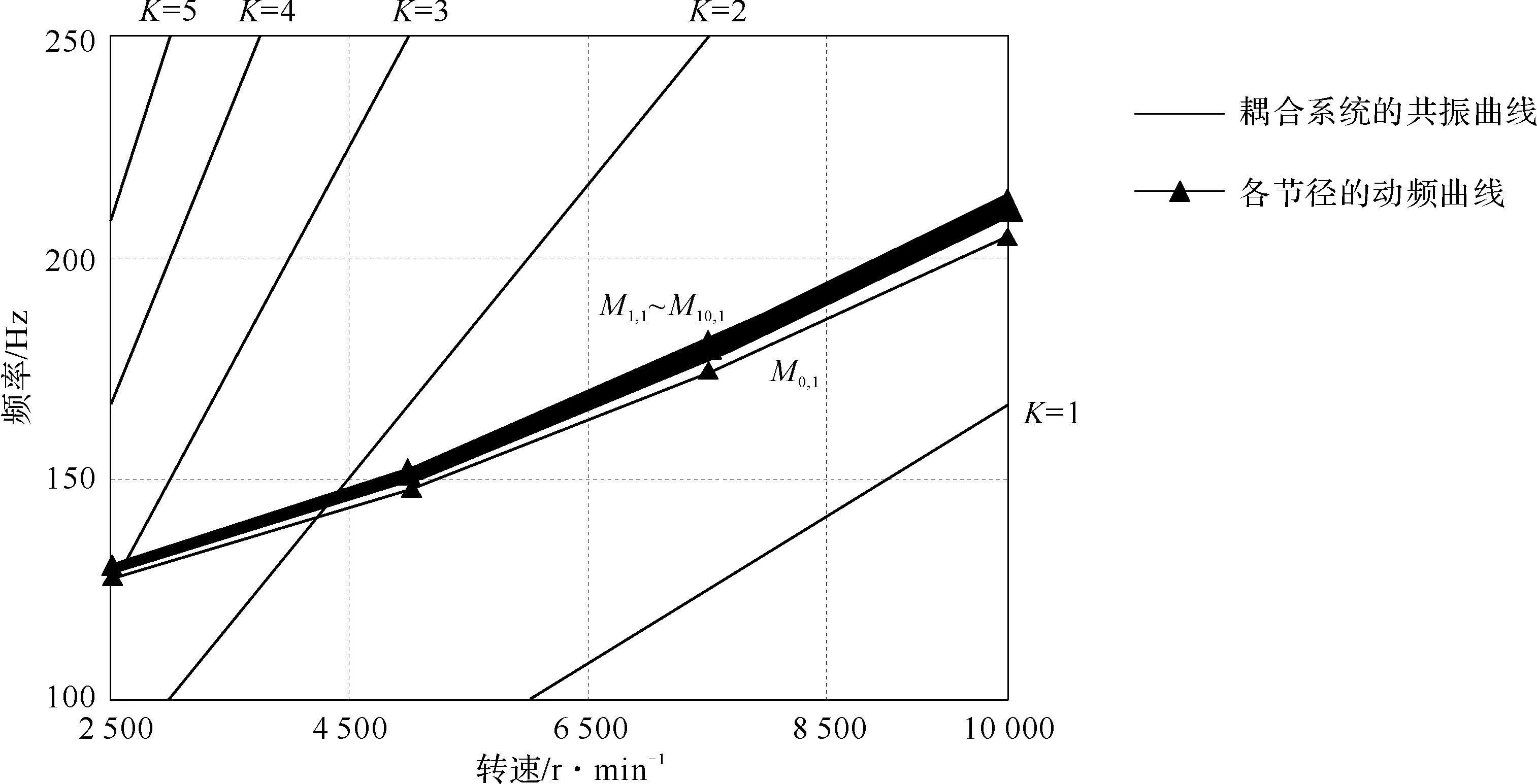
图44 考虑接触摩擦特性的叶片-盘组合结构的Campbell图

图45 未考虑接触摩擦特性的叶片-盘组合结构振动的Campbell图

从图44和图45均可以看出，从最低转速到最高转速，节径数mbd=1和节径数mbd=4～10的1阶频率线远离相应激振频率线，而节径数mbd=2～3对应的1阶频率与相应的激振频率线都有交点，因此很可能引起节径数mbd=2或mbd=3下的一阶振动。

在图44中，考虑CFC的各节径对应的1阶固有频率值，最大频率差值为节径数mbd=0和节径数mbd=10对应的固有频率，为9.83 Hz；最小频率差值为节径数mbd=9和节径数mbd=10对应的固有频率，为0.17 Hz。可以发现，随着节径数的增加，BD的固有频率差值越来越小，更加接近于叶片本身的固有频率。

在图45中，未考虑CFC的各节径对应的1阶固有频率值，最大频率差值为0.37 Hz；最小差值为0 Hz。这说明未考虑CFC时，节径数对第一阶固有频率的影响比考虑CFC时小。

6 自带冠叶片(ISB)结构中的叶冠碰撞摩擦特性分析

6.1 叶冠间碰撞摩擦的物理过程

叶冠碰撞摩擦过程(collision friction process of blade shrouds)基本上可以划分为分离(separation)和接触碰撞(contact collision)等两个阶段。在分离阶段，叶冠之间没有相互作用力；在接触碰撞阶段，叶冠之间相互碰撞，其作用力有两种形式，一是叶冠间的不同紧度提供的不同接触正压力(法向力)，二是粘滞、滑移运动导致的冠间摩擦(切向力)。由于碰撞力和摩擦力的联合作用，使得叶冠之间的接触情况非常复杂，具有典型的非线性特征，工程中一般只能进行分析研究和特例校核。

为了便于研究，叶片的接触碰撞常常需要做一定的简化。目前，许多学者提出了多种无润滑接触的干摩擦阻尼模型(Dry Friction Damping Model without Lubricated Contact，DFDMLC)[41-42]，目前常用的简化模型有宏观滑移模型(Macro-Slip Model，MaSM)和微观滑移模型(Micro-Slip Model，MiSP)。

宏观滑移模型(MaSM)属于单点接触模型，假设接触面内所有接触点的正压力都相等，即所有点同时滑动或粘滞，按照是否考虑接触面的刚度又分为Sgn宏观滑移模型和考虑接触刚度的宏观滑移模型等两种摩擦模型。

Sgn宏观滑移模型忽略了接触刚度，是一种最简单的摩擦模型，其接触点描述见图46。由于模型中忽略了接触刚度，两个接触物体之间不是总保持滑动状态就是总保持粘滞状态。Sgn宏观滑移模型描述的是理想状况下的干摩擦模型，很多情况下不能准确估计摩擦阻尼的减振效果。

N*为正压力，μ为摩擦系数；x为位移形式的外激励；u为阻尼器的位移。

Sgn宏观滑移模型建立在一种理想的干摩擦情况下，与实际情况不符。实际情况是干摩擦接触面两端的变形不是突然发生的，当外力小于干摩擦力时，接触面的两端仍然有变形，因为接触点本身具有一定的弹性，所以接触面上干摩擦力仍然不是常数，而是随着振幅的加大而缓慢上升的。

考虑接触刚度的宏观滑移模型考虑了在接触面产生相对滑动之前的变形问题(见图47)，即将一个弹簧与一个理想库仑阻尼器单元串联起来。

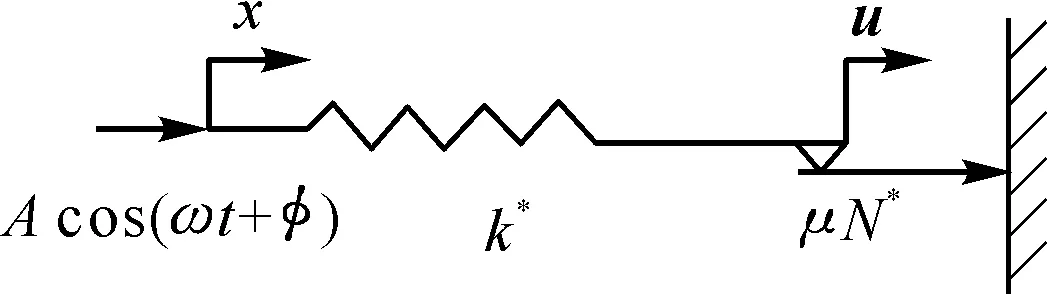
A为位移幅值；k*为弹簧刚度。

在假设位移x正弦变化时，该串联弹簧/阻尼器模型的力与位移的关系可表述为图48。由图48可以看出，该模型的轨迹为闭合的平行四边形。

图48 摩擦力与位移的关系

设系统受到简谐激励du=Bcosθ，θ=ωt-φ(B为摩擦面间稳态相对振动幅值；ω为激励频率；φ为相位差)。在周期性作用力下，两接触面间的力与位移的关系表现为一条迟滞回线(见图48)。其中，a点θ=0，由滑动转为粘滞；b点θ=θ*，由粘滞转为滑动；c点θ=π，由滑动转为粘滞；d点θ=π+θ*，由粘滞转为滑动。

微动滑移模型(MiSP)描述的接触面为多点接触，叶片的振动可能只会导致部分接触点发生滑移，而其他接触点仍保持粘滞状态。MiSP主要包括串联MiSP和并联MiSP等两种形式。并联MiSP比串联MiSP更加适合于进行动力分析，故而工程应用中往往选择并联MiSP作为研究工具。

MaSM假设接触面内所有接触点的正压力相等，即所有点同时滑移、粘着或分离。MiSP因其复杂性使得它目前只能停留在理想化的摩擦阻尼元素上作理论性的研究。本研究团队在叶片振动分析中采用基于Coulomb摩擦定律的MaSM——假设两个接触面值之间不是处于滑移状态，就是保持滑动状态，摩擦力等于一个常数乘以法向的正压力。

6.2 叶冠间接触碰撞弹性力与阻尼力模型

叶冠间的接触碰撞力是通过接触变形来传递的，碰撞力由变形过程中的非线性表面弹性力Fk和非线性表面阻尼力Fc组成[42]。

6.2.1 接触碰撞弹性力模型

【假设5】 自带冠叶片(ISB)叶冠间的接触碰撞过程中接触表面不发生塑性变形，将其视为弹性球(elastic ball)与弹性体(elastic body)的碰撞(见图49)。

P为外载荷；a为接触圆半径；R1为弹性球球面半径；R2为弹性体半径，R2→+∞；d为弹性变形。

根据弹性球与弹性体接触的弹塑性理论及文献[27]，可以得到弹性球与弹性体接触圆半径a与外载荷力P之间的关系。

(141)

式中，μ1为弹性球的泊松比；μ2为弹性体的泊松比；E1为弹性球的弹性模量；E2为弹性体的弹性模量；K1为弹性球的刚度；K2为弹性体的刚度。

图49为弹性变形d与接触圆半径a的几何关系，可以表示为如下形式。

(142)

因为R2→+∞，所以

(143)

将式(143)带入式(141)，可得

(144)

令k表示冠间接触碰撞过程中的弹性力系数,则有

(145)

于是

(146)

ISB发生冠间接触碰撞时，叶冠的弹性变形可表示为如下形式。

d=v-Δ

(147)

式中，v为叶冠处的位移；Δ为叶冠间的初始间隙。

ISB冠间双侧对称碰撞的接触弹性力(contact collision elastic force between ISB)Fk可表示为如下形式。

(148)

式(148)所揭示的冠间接触碰撞弹性力Fk与ISB叶冠位移v之间的关系见图50。

图50 冠间接触碰撞弹性力和叶冠位移的关系

6.2.2 接触碰撞阻尼力模型

在Coulomb摩擦模型(Coulomb Friction Law，CFL)中，力与速率的关系见图51[49]。

图51 Coulomb摩擦定律中力与速率的关系

在CFL中，摩擦力是不连续的，其力和速率的关系可表示为如下形式。

(149)

式中，Ff为摩擦力；μ为滑动摩擦系数或称动摩擦系数；FN为两个物体间的法向力；vrel为两个接触面间的相对滑动速率。

为简洁起见，可将CFL简写为如下形式。

Ff=-μFN·sgn(vrel)

(150)

式中，sgn为符号函数，在其参数为正数、负数和零时分别为1、-1和0[注]。

[注] sgn函数的概念只是在滑动状态时是正确的，而在界面处于粘着状态时，vrel在一定长度时间内为零，在这种情况下，Ff介于-μsN～μsN之间，μs为静摩擦系数。

由于摩擦力呈非线性，导致系统的运动方程也随之呈现为非线性，对此，工程上通常采用近似解法(approximate solution)。从工程应用的观点观察，如果摩擦力Ff较大，运动将出现间断，甚至停止，因此不会引起振动危害，不一定要研究它。在很多情况下，与激励力相比，摩擦力相对较小，这时可将响应近似为简谐运动(simple harmonic motion)来处理[49]。通常采用的方法是将摩擦力等效为粘性阻尼力(viscous damping force)，使两者所作的功相等，从而求得等效粘性阻尼系数(Equivalent Viscous Damping Ratio，EVDR)Ceq。

假定响应为简谐运动，则有

x=X0sin(ωt)

(151)

式中，x为振动位移；X0为振动振幅；ω为振动圆频率或称角频率；t为时间。

每一周期内消耗的功可表述为如下形式。

(152)

式中，ΔE为一个周期内消耗的功；T为简谐运动的周期。

根据粘性阻尼耗散能量的相关理论，粘性阻尼一周消耗的功可表述为如下形式[54]。

(153)

可得等效粘性阻尼系数(EVDR)

(154)

6.3 叶冠间碰撞的解析模型

一般来说，航空发动机叶片具有复杂的气动外形，要直接对其动力学特性进行细致分析并找出精确计算解，存在诸多困难。但是，如果对其进行合理简化(例如，将叶片简化为旋转态悬臂梁模型(RCBM))，就可以对其进行精确的动力学建模，通过数值计算做出定性及初步定量分析，从而对叶片的振动特性做出合理估算，进而解释叶片某些振动现象的本质。这类方法在实际的叶片设计及维修中，对于分析问题、解决问题有着十分便捷的实际作用[57]。

6.3.1 动力学微分方程的建立

航空发动机叶片是一种弹性结构(elastic structure)，以弯曲(bending)、扭转(torsion)及弯扭耦合(bending-torsion coupling)等振动形式为主。因此，可以将发动机叶片等效为旋转悬臂梁模型(RCBM)。考虑到ISB顶端装配有叶冠，且在叶片实际工作中相邻叶冠之间有碰撞与摩擦的作用，故将ISB叶冠间的接触碰撞简化为弹簧与带有间隙的干摩擦阻尼约束模型(Constraint Model of Spring and Day Friction Damping with Gaps，SDFDG-CM)[57]。ISB叶冠间碰撞的解析模型(Analytical Model of Collision between Shrouds，CS-AM)见图52。

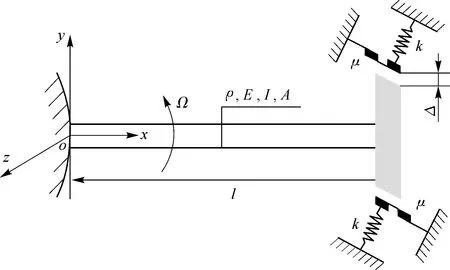
Ω为叶片的转速；ρ为密度；E为杨氏模量；I为惯性矩；A为横截面积；μ为摩擦系数。

在ISB的实际结构中，叶冠之间存在某一接触角度γ，即干摩擦阻尼接触角(contact angle of dry friction damping)(见图53)，叶片末端所受碰撞正压力FN和摩擦力Ff的受力分析见图54。

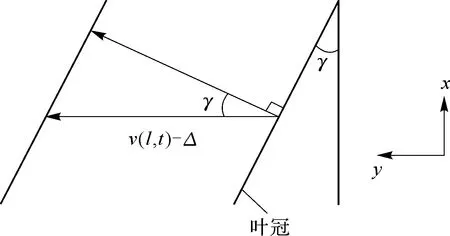
v(l,t)为叶冠沿y轴方向的位移；γ为干摩擦阻尼接触角；Δ为为叶冠初始间隙。

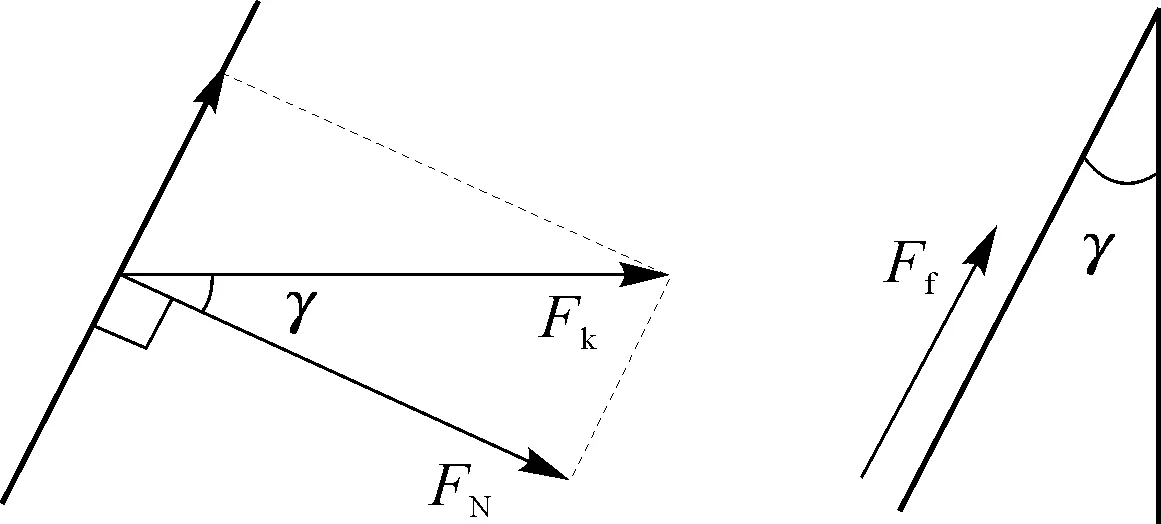
FN为正压力；Fk为自带冠叶片冠间接触碰撞弹性力；Ff为摩擦力。

由图54，可以得到如下结果。

(155)

(156)

式中，μs为静摩擦系数；μk为动摩擦系数。

由力与力矩平衡原理对旋转悬臂梁模型的微元体dx进行受力分析，并考虑叶冠之间的碰撞正压力FN和摩擦力Ff的影响，可以列出如下形式的旋转态悬臂梁叶片的非线性动力学微分方程(Nonlinear Dynamic Differential Equation of RCBM，NDDE-RCBM)。

(157)

式中，ρ为悬臂梁的密度；A为横截面积；EI为弯曲刚度(flexural rigidity)；f(x)为离心力；Q(t)为周期性气动激振力；δ(x)为脉冲函数。

规定δ(x)满足如下形式。

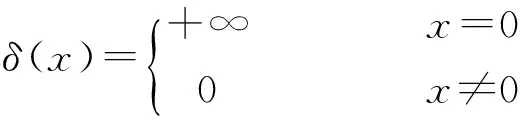
(158a)

(158b)

6.3.2 动力学方程的离散化

利用连续系统响应的振型叠加法(mode superposition method)将式(157)离散化，并取前三阶模态进行模态截断(modal truncation)。

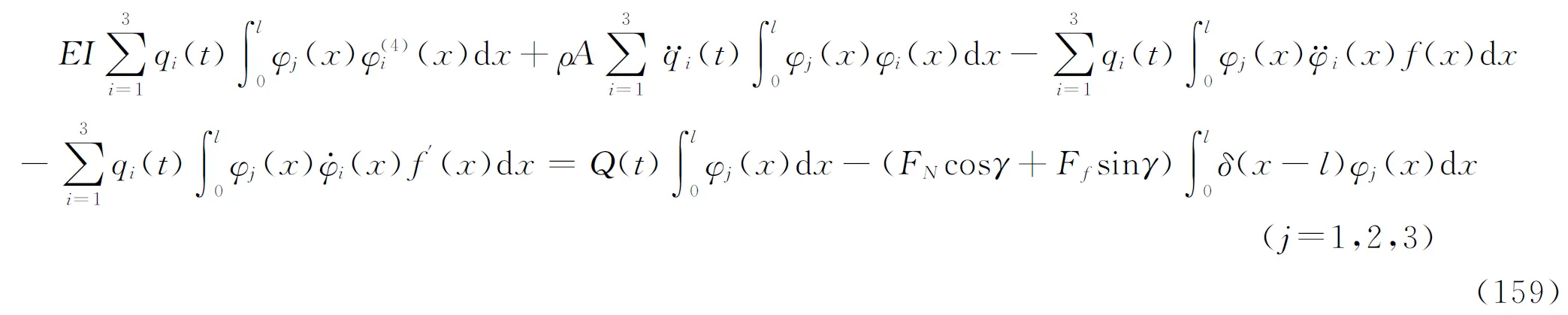
式中，qi(t)为广义坐标(正则坐标)；φi(x)为第i阶模态的模态函数；φj(x)为第j阶模态的模态函数。

为方便表达和计算，记

(160a)

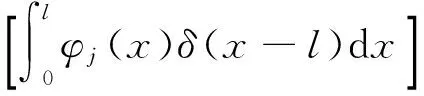
(160b)

根据δ(x)函数的性质

(161)

可得

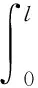
(162)

所以

A7=[φj(l)]3×1j=1,2,3

(163)

在实际计算中，为了在程序中更加方便地在叶冠处施加碰撞正压力FN和摩擦力Ff，其表达式采用如下3种函数形式[61]。

(1) 对称碰撞(symmetric collision)

(164)

(2) 单侧碰撞(unilateral collision)

(165)

(3) 双侧非对称碰撞(bilateral asymmetric collision)

(166)

式中，Δ1为y正方向上的间隙；Δ2为y负方向上的间隙；Δ1和Δ2均为正值。

6.4 叶冠间碰撞的有限元模型

基于Euler-Bernoulli梁单元理论，建立叶冠间碰撞的有限元模型(Finite Element Model of Collision between Shrouds，CS-FEM)(见图55)[40]。

图55 叶冠间接触碰撞的有限元模型

ISB根部采用固支形式，将叶片分为15段，即15个单元和16个节点。由于碰撞和摩擦发生在叶冠处，取第15节点为研究对象，计算观察叶冠之间发生碰撞后叶片的响应特性，并以f表示周期气流激振力的频率(Hz)，将叶冠之间的接触碰撞简化为叶冠与弹性限位之间的碰撞。

叶冠接触碰撞的动力学方程可以写为如下形式。

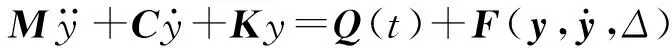
(167)

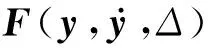
CS-FEM的结构阻尼采用瑞利阻尼(rayleigh damping)形式[60]，其表达形式如下。

C=αM+βK

(168a)

(168b)

(168c)

式中，α和β为比例系数(proportionality coefficient)；ξ1为第一阶模态阻尼比；ξ2为第二阶模态阻尼比；ω1为第一阶弯曲固有频率；ω2为叶片的第二阶弯曲固有频率。

运用数值计算方法对式(167)求解，可以得到叶片的振动响应。

6.5 叶冠间接触碰撞的数值算例

为了验证所建立的CS-AM和CS-FEM对模拟降低航空发动机ISB强迫振动响应问题的有效性和收敛性，以及ISB随转盘旋转速度Ω、相邻叶冠之间的初始间隙Δ，相邻叶冠之间的接触弹性系数k等参数对于ISB强迫振动特性的影响，需要通过算例进行验证，并根据得到的计算结果和结论给予分析。

若假设气流激振频率为转频的3倍，作用在叶片上的气动力为周期性气流激振力(periodic flow induced force)，将其进行三角级数(trigonometric series)展开，取第一周期项[41]，则有如下表述形式。

Q(t)=F0sin3Ωt

(169a)

Ω=2πn/60

(169b)

式中，Q(t)为气动力，N；F0为气流激振力幅值，N；Ω为叶片随轮盘转动的旋转频率，rad/s；n为转速，r/min。

将一组较为常见的航空发动机ISB的材料参数和几何参数作为算例参量(见表10)[57]。

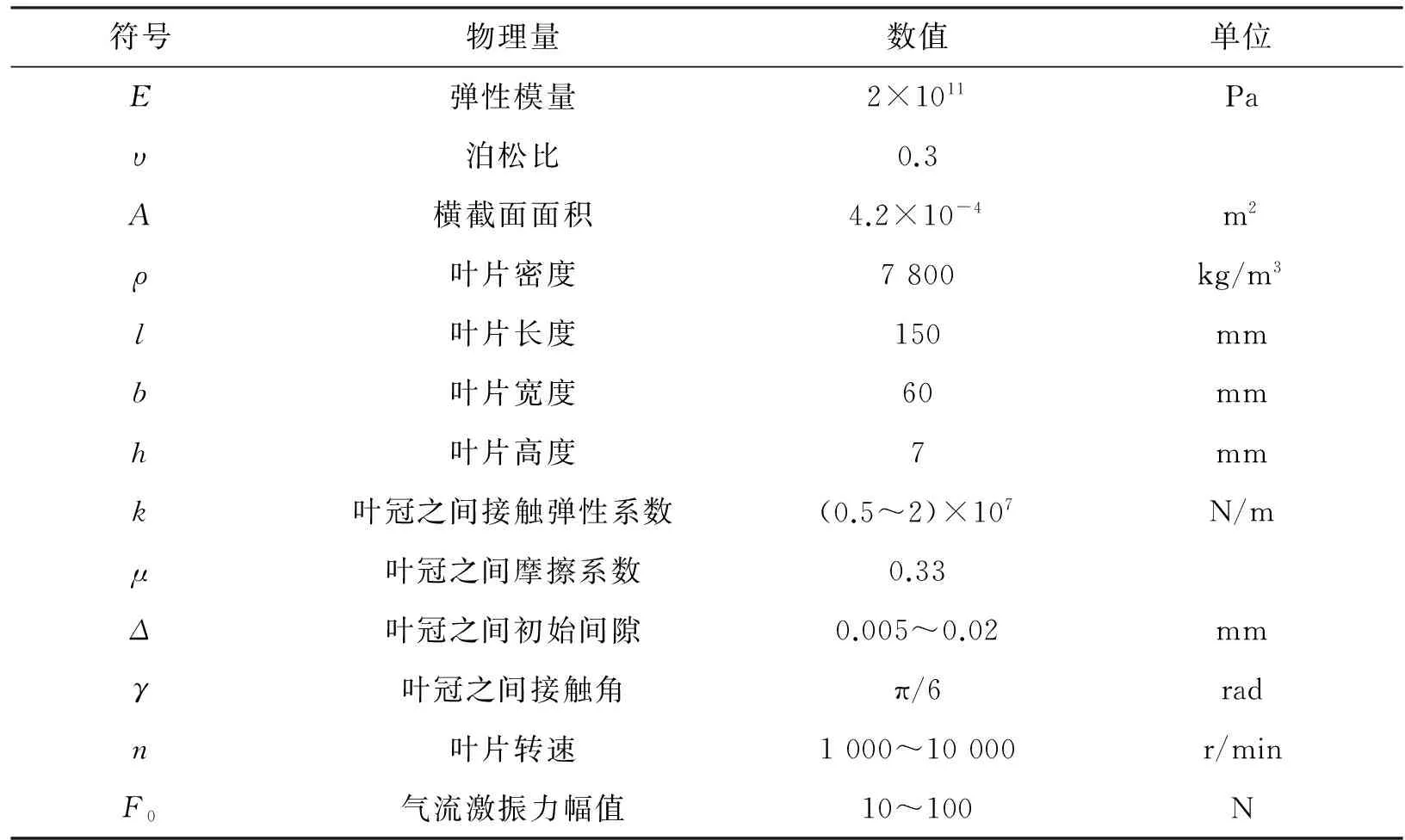
表10 系统的材料参数和几何尺寸参数

为了便于观察和分析叶片振动的现象，在不失计算准确性的前提下，采用少节点自由度以减小计算机的计算量。采用CS-AM计算时，取前三阶模态计算；采用CS-FEM计算时，设定节点的自由度为2自由度，即单元变形只有横向位移v和转角θ。

6.5.1 叶片转速对自带冠叶片振动的影响分析

为了分析叶片转速发生变化时，叶冠干摩擦阻尼对于叶片系统振动的影响，提出如下假设。

【假设6】 转子转速的变化范围为100～10 000 r/min，且转子的转速从低速向高速不断增加；叶片叶根距离转轴的轴心线为R0=l；叶冠之间的初始间隙为Δ=1.5×10-5m；叶冠接触碰撞刚度kc=1×107N/m。

基于matlab.对CS-AM和CS-FEM进行数值计算，得到转子转速与叶片振动的关系曲线(见图56)。为了保证数值算法绝对收敛，且将系统的瞬态响应尽快衰减，本算例中的阻尼系数取值为ξ1=0.4，ξ2=0.4。

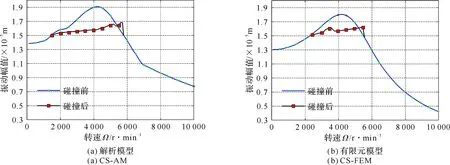
图56 转子转速与叶片振动幅值的关系曲线

从图56可以观察到，如果叶冠之间的初始间隙足够大，叶片叶冠处的振动位移将不足以达到与相邻叶冠相互接触，因此不能发生碰撞和摩擦。在这种情况下，叶片弯曲弹性振动的位移将伴随着转子转速的不断升高而逐渐增大，当转速达到4 100 r/min时，叶片发生共振，此时叶片的振动位移达到最大。随后，随着转速增大叶片的振动幅值将逐渐减小。可以预见，当达到叶片下一阶共振转速时，叶片的振动幅值又将增大至另一峰值。

由以上分析可知，当叶片转速达到共振转速时，叶冠之间最有可能发生碰撞或者说碰撞最为严重。

以CS-FEM的计算结果(见图56(b))为例，当转速低于2 100 r/min时，叶冠处弯曲振动位移小于叶冠间隙Δ，此时叶冠之间未发生碰撞。当转速继续升高，直至超过2 100 r/min时，此时叶冠处的振动位移大于冠间的初始间隙，从而在冠间发生碰撞摩擦，这时干摩擦阻尼(dry friction damping)将发挥作用。随着转速的继续升高，叶片振动幅值并没呈现出未发生碰撞前随转速振动幅值增大的现象，而是在一段转速区域内呈现幅值缓慢递增的态势。这是由于干摩擦阻尼相互碰撞摩擦消耗了振动产生的部分能量，从而起到了抑制叶片振动的作用。当转速继续升高直至超过了叶片的共振转速区时，叶片的振动位移也随之减小，当达到约6 000 r/min时，叶片的振动振幅低于叶冠之间的初始间隙值，所以不会再发生碰撞，直至到达下一个共振转速区才能再次发生碰撞。

6.5.2 叶冠间对称接触碰撞响应特性分析

6.5.2.1 叶冠碰撞响应特性

【假设7】 叶冠之间的干摩擦阻尼初始间隙Δ=1×10-5m，叶冠接触碰撞刚度kc=1×107N/m。

【工况一 转速n=2 000 r/min】

(1) 无碰撞摩擦 当叶片只受气流激振力的作用，而无叶冠之间的碰撞摩擦作用时，分别采用CS-AM和CS-FEM计算叶冠的振动响应，其时域图、相轨迹图和频谱图见图57。

图57 转速n=2 000 r/min且无碰撞时叶片的振动响应特性

从叶冠处的响应时域波形图可以看出其时域响应是正弦波形，其相轨迹图是一正椭圆，在频谱图中只反映出激振频率f=[(3×2 000)/60] Hz=100 Hz。这些响应特征都说明只在气流激振力的作用下，叶片的运动状态是简谐振动，而且叶片的强迫振动已经达到稳定状态。

(2) 有碰撞摩擦 当考虑叶片叶冠之间的碰撞摩擦作用时，按给定的初始间隙和接触刚度等条件，分别基于CS-AM和CS-FEM计算ISB叶冠振动响应(见图58)，获得其时域图、相轨迹图和频谱图，以及相邻叶冠之间的碰撞力时域波形及碰撞力的幅频特性等，同时也给出了其时域响应及碰撞力的局部放大图。

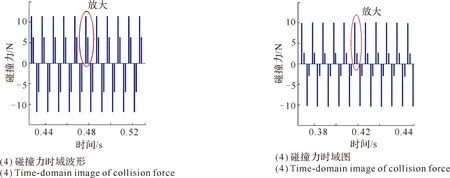
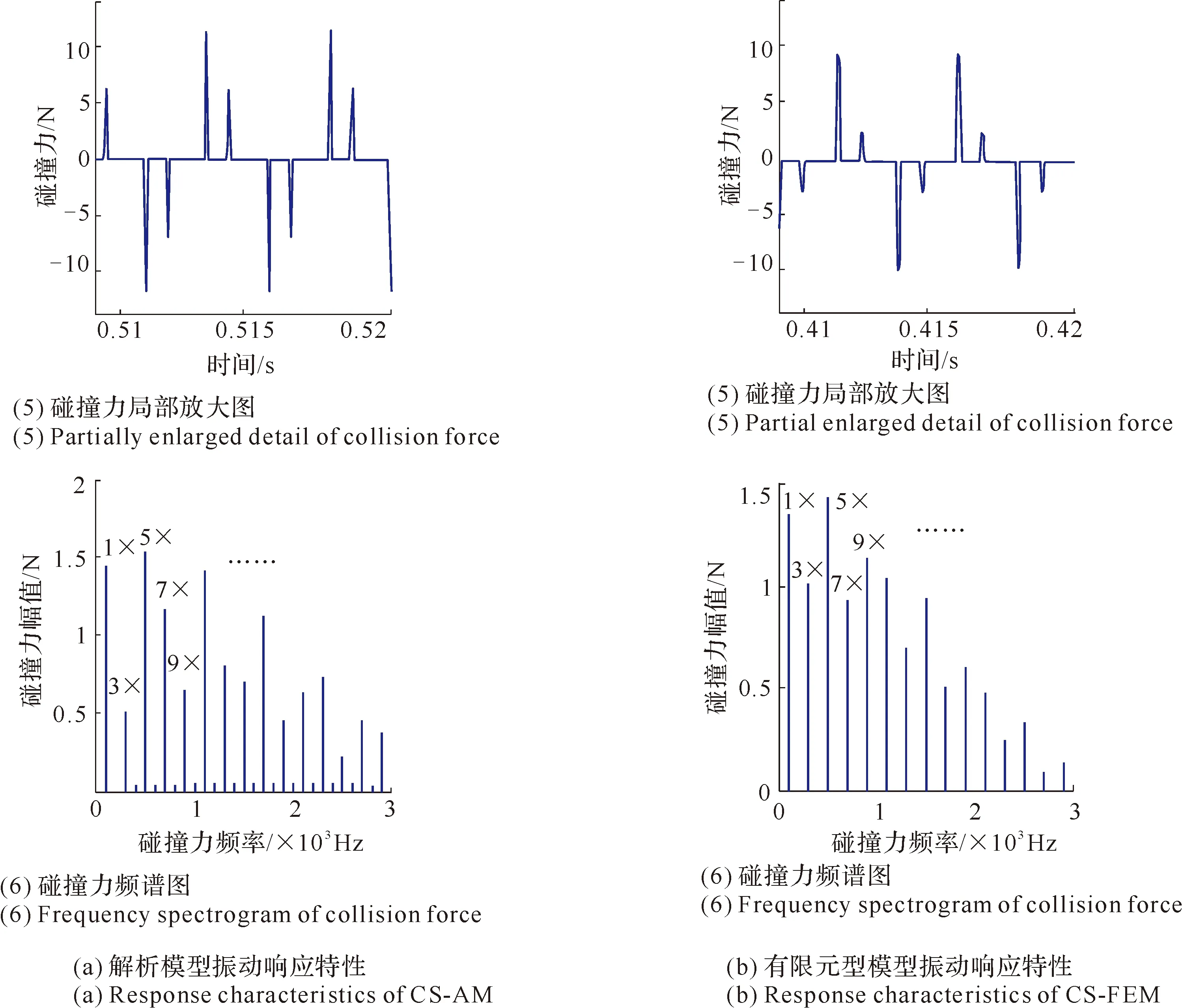
图58 转速n=2 000 r/min且有碰撞时叶片的振动响应特性

从叶冠处的时域响应，以及碰撞力响应的局部放大图中可以看出，叶片在气流激振力的频率为f=100 Hz时一个周期内发生了2次碰撞；而且从碰撞力的幅频特性图中可以看出，碰撞力的频率成分是由气流激振力频率的奇次倍频组成，从响应的幅频特性曲线中也可以看出，对应激起的响应的频率成分亦是由激振力频率的奇次倍频组成(这与前文做出的定性分析取得了一致性)，这也使得叶片的振动能量被分散在了这些高阶的奇次倍频上，而不是集中在气流激振力的频率下，因而起到了抑制叶片振动的作用。对比图57和图58还可以看出，碰撞后叶冠处的振动幅值比碰撞前已有减小，基本在设定的间隙值左右，这说明叶片的振动得到了很好的抑制。

【工况二 转速n=4 100 r/min】

(1)无碰撞摩擦与在转速n=2 000 r/min工况下类似，可得在转速n=4 100 r/min工况下的叶片振动响应(见图59)。

从图59中可以看出，在频谱图中只反映出激振频率f=[(3×4 100)/60] Hz=205 Hz。与在转速n=2 000 r/min工况下类比分析可知叶片的强迫振动已经达到稳定简谐振动状态。

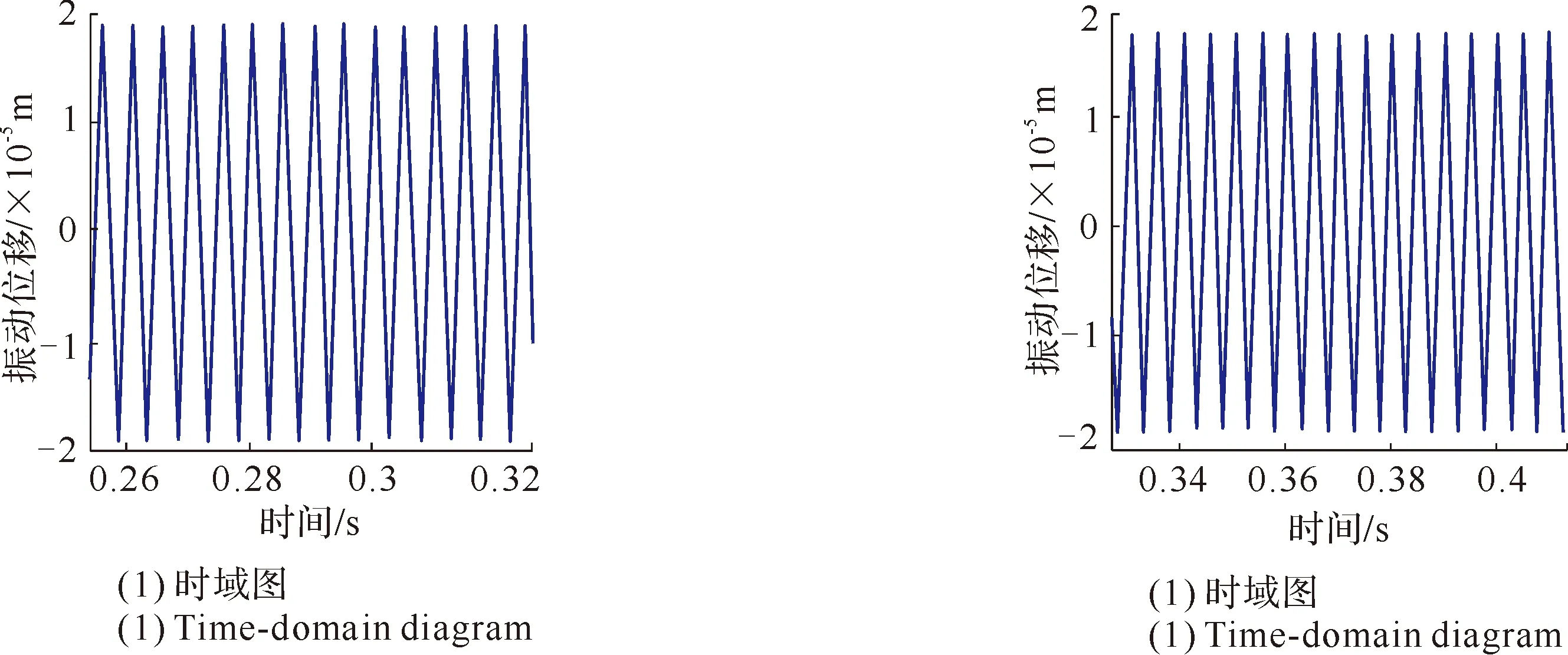
图59 转速n=4 100 r/min且无碰撞时叶片的振动响应特性

(2) 有碰撞摩擦 与在转速n=2 000 r/min工况下类似，考虑叶片叶冠之间的碰撞摩擦作用，按给定的初始间隙和接触刚度等条件计算，可得在转速n=4 000 r/min工况下的叶片振动响应等(见图60)。

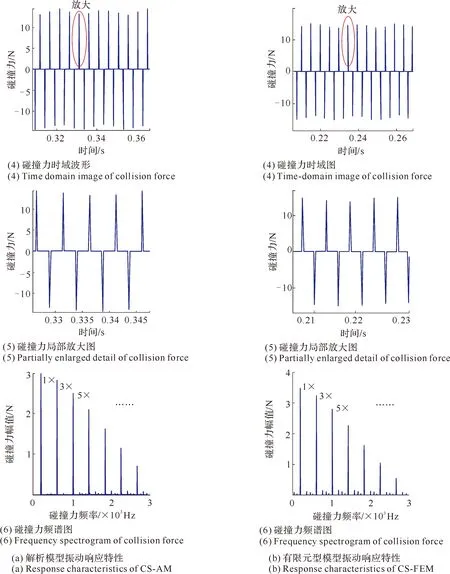
图60 转速n=2 000 r/min且有碰撞时叶片的振动响应特性

从叶冠处的时域响应以及碰撞力响应的局部放大图中可以看出，叶片在气流激振力的频率为f=205 Hz时一个周期内发生了1次碰撞。

图61为转子转速分别在1 000，2 000，3 000，4 100，6 000，7 000 r/min的相轨迹图，从相轨迹图的变化亦可以看出叶冠之间从发生接触碰撞到分离的整个过程。

图61 叶冠处相轨迹随转速的变化

6.5.2.2 叶冠间碰撞摩擦的三维谱振图分析

若叶冠之间的初始间隙为Δ=1×10-5m，叶冠接触碰撞刚度kc=1×107N/m。考察叶片叶冠处在转子转速从0 r/min到10 000 r/min升速过程中的三维谱振图(见图62)。

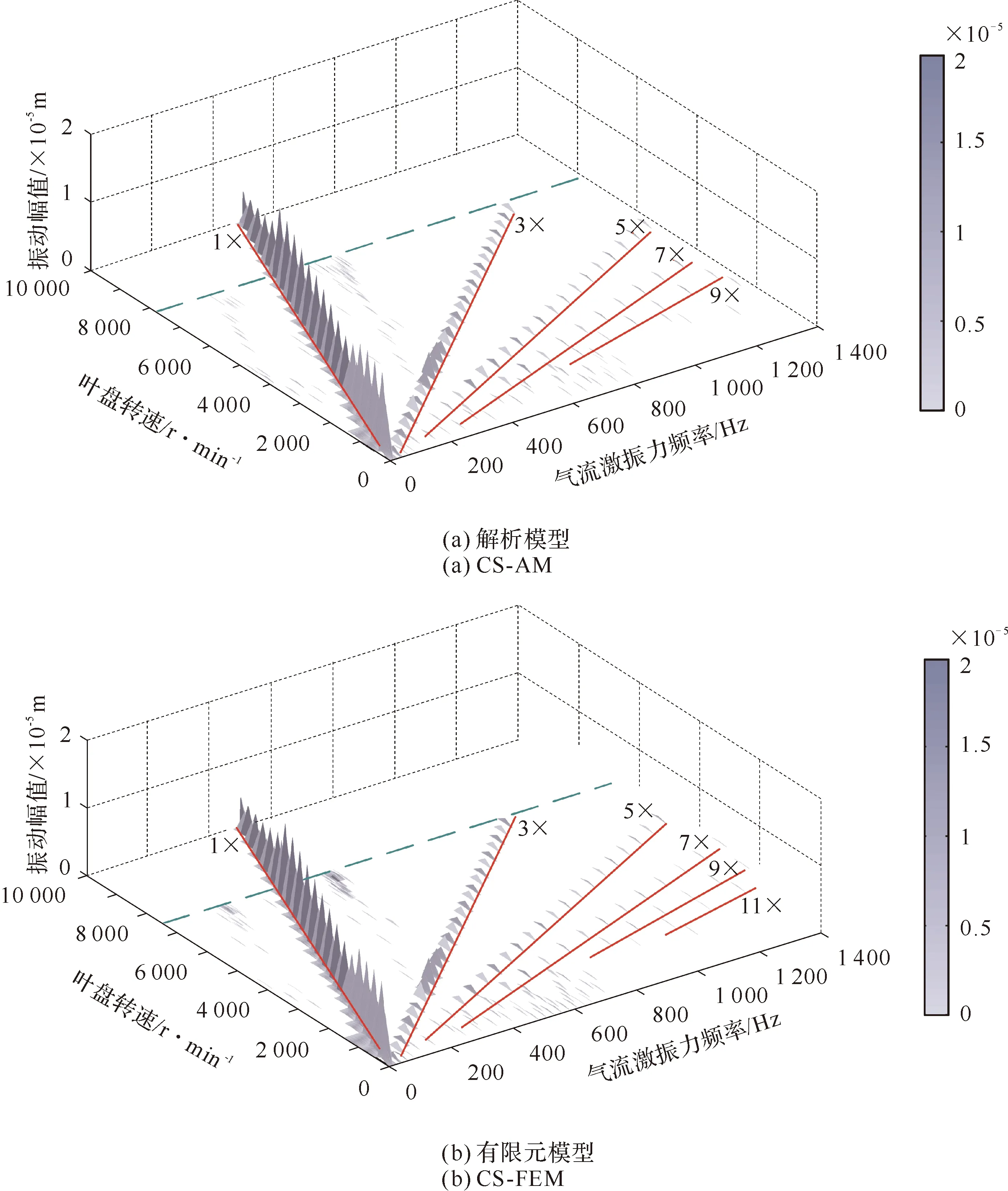
图62 叶冠间碰撞摩擦三维谱振

从图62可以清晰看出，ISB叶冠之间发生双侧对称碰撞摩擦后，叶冠处的响应具有丰富的谐波成分，且以1×，3×，5×等奇数倍频为主，随着谐波次数的逐渐升高，其幅值逐渐减小。在叶盘转速达到约7 000 r/min以后，由于叶片叶冠处的振动幅值小于冠间的初始间隙，以至相邻叶冠之间不能再发生碰撞摩擦。反映在三维谱振图上为转速在约7 000 r/min以后，其幅频特性均只含有气流激振力的频率成份，奇数高倍频成份消失。

6.5.2.3 叶冠间间隙对碰撞响应的影响

为分析航空发动机带冠叶片自由末端相邻叶冠之间的初始间隙Δ，以及转子转速对叶冠之间发生碰撞摩擦后叶冠处的动力学响应特性的影响，做如下假设：若相邻叶冠之间的间隙变化范围为0.01～0.02 mm，转子转速的变化范围为0～10 000 r/min，叶冠接触刚度kc=1×107N/m。通过计算得到转子转速及冠间初始间隙与叶冠处弯曲振动幅值变化的关系(见图63)。

图63 转子转速和冠间初始间隙与弯曲振动幅值的关系

从图63可以观察到，在给定相邻叶冠间隙的情况下，随着转子转速的升高，求解得到的响应幅值会逐渐增大，当振动位移达到冠间初始隙值时，由于干摩擦阻尼的存在，叶冠之间会发生接触碰撞，这时随着转速的增加叶冠处的振动位移幅值呈现出缓慢升高的态势，这说明干摩擦阻尼通过冠间的接触碰撞消耗了叶片振动的能量，起到了很好的振动抑制效果。

从图63还可以观察到，相同转速情况下，相邻叶冠间的间隙越小，振动响应的幅值越低，即能更好地抑制叶片的振动。这反映出当相邻叶冠间隙偏大时，叶片发生弯曲振动时的振幅未能达到促使两相邻叶冠间发生接触，此时干摩擦阻尼并不能很好地发挥作用，叶片的振动能量就不能得到有效的耗散，因此减振的效果并没有体现。因此，为了更好地抑制航空发动机叶片的振动，在设计、制造及安装方便可行的情况下，应该尽量地缩小叶冠之间的间隙。

6.5.2.4 叶冠间接触刚度对碰撞响应的影响

为分析ISB自由末端相邻叶冠间的接触刚度kc，以及转子转速对叶冠之间发生碰撞摩擦后叶冠处的动力学响应特性的影响，取相邻叶冠之间的接触刚度变化范围为0.5×107N/m～2×107N/m，转子转速的变化范围为0～10 000 r/min。设定冠间初始间隙Δ=1×10-5m。转子转速及叶冠间接触刚度与叶冠处弯曲振动幅值变化的关系(见图64)。

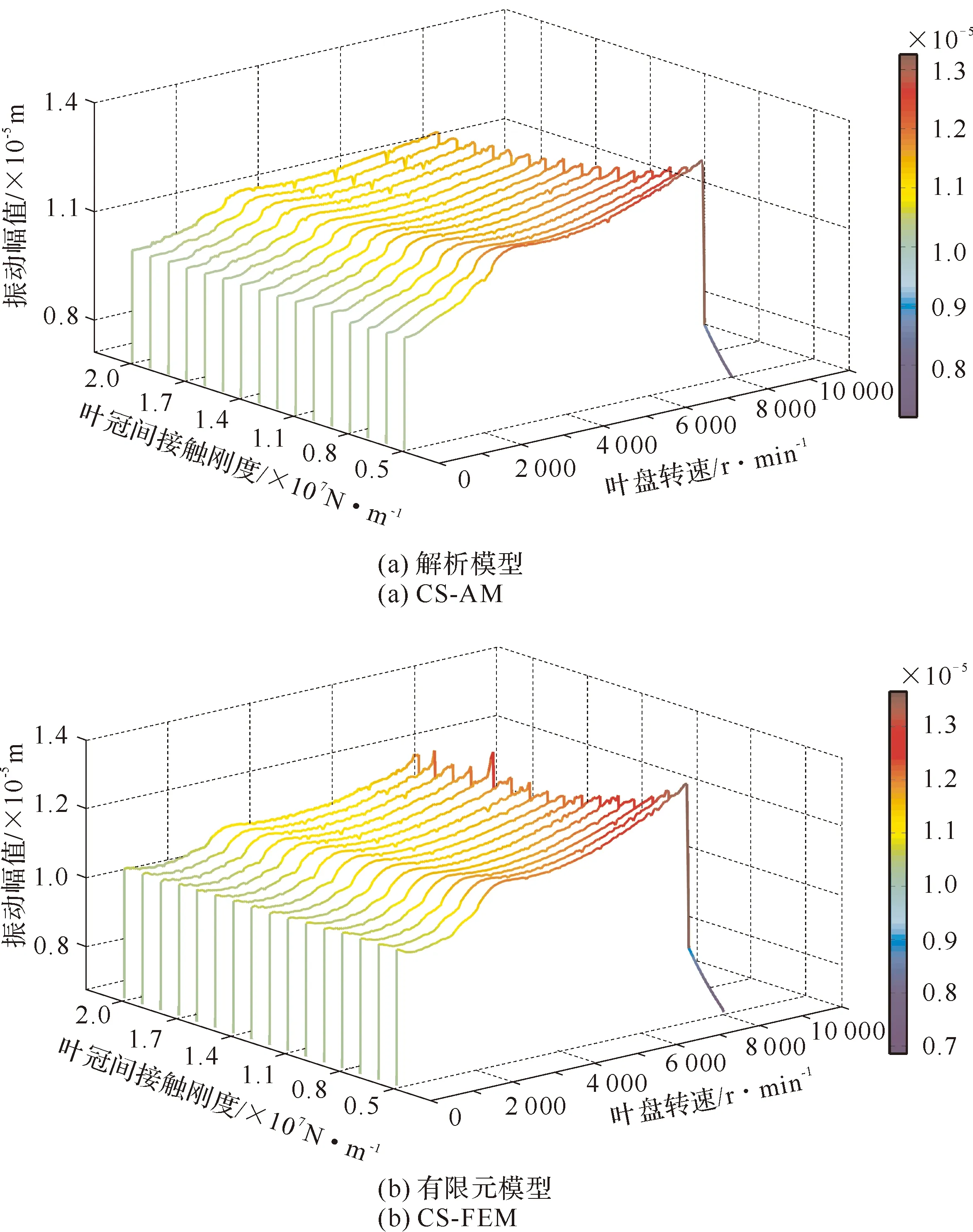
图64 转子转速和冠间弹性系数与弯曲振动位移幅值的关系

由图64中可以观察到，在给定相邻叶冠间的弹性系数的情况下，随着发动机转子转速的升高，求解得到的响应幅值会逐渐地增大，当振动的幅值达到相邻叶冠间隙值时，干摩擦阻尼会产生碰撞和摩擦的作用。此时，伴随着转速的升高，振动幅值并没有迅速地增大，而是呈现出缓慢升高的态势，这是干摩擦阻尼通过冠间的碰撞摩擦耗散了叶片振动的能量的结果。

在相同的转速下，加大弹性系数对叶片振动的影响并不是很显著，振动幅值会稍微减小。究其原因，当叶冠发生碰撞时，大的弹性系数会产生相对较大的正压力，摩擦力也会随之增大，以达到耗散叶片振动更多的能量，起到更好的振动抑制的效果。因此，为了更好地解决航空发动机转子叶片的振动抑制问题，使干摩擦阻尼的抑振效果更好，应该尽量选择弹性系数较高的材料作为叶冠干摩擦阻尼的表面材料。但是，过大的弹性系数会使叶冠碰撞时产生很大的碰撞力，这对叶片的使用寿命会造成不利的影响，加之弹性系数对减振效果的影响并不像冠间间隙那样显著，因此，设计叶片时须要根据实际情况慎重选择。

6.5.3 叶冠间非对称接触碰撞响应特性分析

由于叶片的制造及安装误差等因素，使得叶片叶冠之间的初始间隙不可能严格的相等。因此，在实际工况下，叶冠冠间可能会发生单侧碰撞摩擦和双侧非对称碰撞摩擦。在前面研究的基础上，以有限元模型为例，考察叶盘转速为2 000 r/min的情况来说明叶冠间非对称碰撞的响应特性。

6.5.3.1 叶冠碰撞响应特性

(1) 单侧碰撞 设叶冠y轴的正方向上的初始间隙Δ=1×10-5m，为了保证叶冠只发生单侧碰撞摩擦，y负方向上的间隙设置为1 m；叶冠接触碰撞刚度kc=1×107N/m。在这种情况下，可以计算得到叶片发生单侧碰撞的时域图、相轨迹图和频谱图(见图65)。

图65 叶冠单侧碰撞振动响应特性

从时域图中可以看到叶片只在y的正方向发生碰撞，且负向的位移有所增大。从相位图中也可清晰地看出叶片发生正向的单侧碰撞。从其频谱图中可以看到，出现了激振力频率的连续奇偶次倍频，也即是说，当叶冠发生单侧碰撞侧时，其振动的能量会分散在激振频率的整数倍频上，并且随着倍频的增大，其能量值减小。对比未发生碰撞时的时域波形(见图57(a))和单侧碰撞时域波形(见图65(a))还可以看到，未发生碰撞的一侧，其振动幅值相对于叶片自由振动时有所增大，这说明在叶冠发生碰撞后，受到的碰撞力与原激振力叠加，使得叶片向另一侧靠近。

(2) 双侧非对称碰撞 若叶冠在y的正方向上的初始间隙Δ1=1×10-5m，在y负方向上的的初始间隙设置为Δ2=1.2Δ1；叶冠接触碰撞刚度kc=1×107N/m。在这种情况下，可以计算得到叶片发生双侧非对称碰撞的时域图、相轨迹图和频谱图，以及相邻叶冠之间的碰撞力时域波形及碰撞力的幅频特性(见图66)。

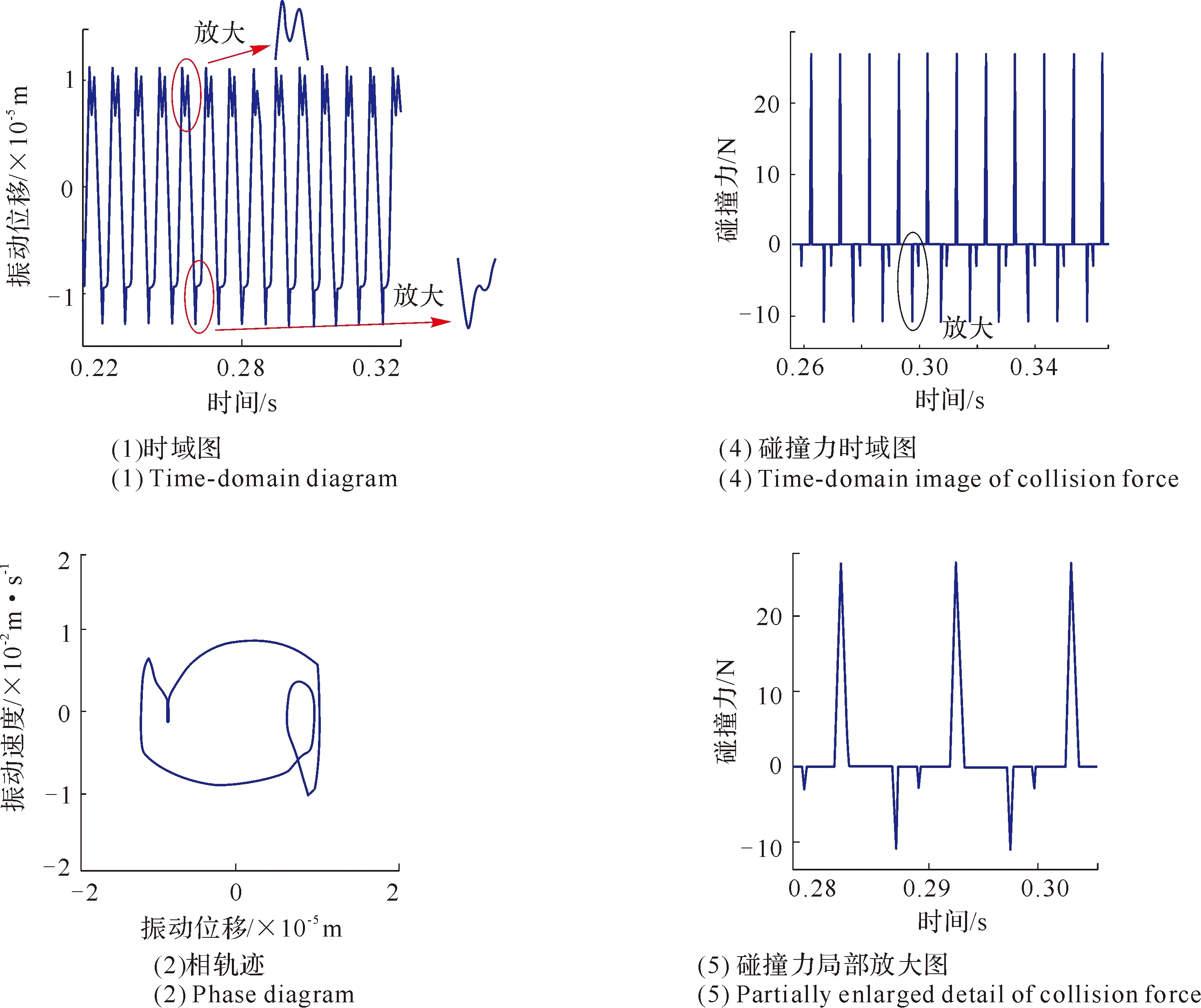
图66 叶冠双侧非对称碰撞振动响应特性

从其频谱图可以看到，叶冠发生双侧非对称碰撞后，其振动的能量会分散在激振力频率的整数倍频上，但是奇倍频的分量大于偶倍频的分量，并且随着倍频的增大，其能量值随之减小。结合前文所述，从叶片发生单侧碰撞摩擦、双侧非对称碰撞摩擦到双侧对称碰撞，这一过程中，其振动的能量从分散在激振频率的整数倍频带上，逐渐地向激振频率的奇倍频带过渡，其偶倍频逐渐地减弱，直至最后消失或是很小的分量。

6.5.3.2 叶冠间碰撞摩擦的三维谱振图分析

若叶片叶冠之间的干摩擦阻尼初始间隙为Δ=1×10-5m，叶冠接触碰撞刚度kc=1×107N/m，考察叶片叶冠处在转子转速从0 r/min到10 000 r/min升速过程中叶冠之间发生单侧碰撞和双侧非对称碰撞后的三维谱振图(见图67)。

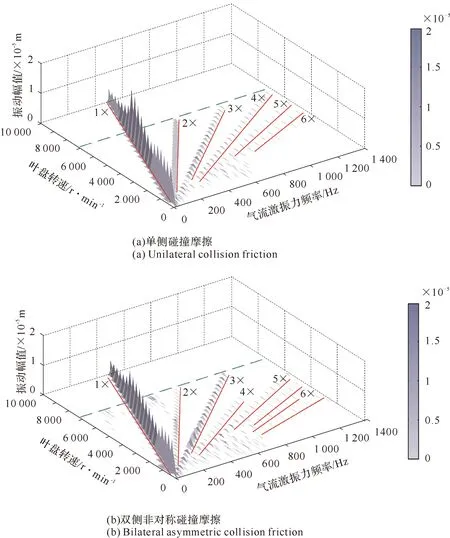
图67 叶冠间碰撞摩擦三维谱振

从三维谱振图中可以清晰看出，在叶片叶冠之间发生单侧碰撞摩擦后，叶冠处响应的谐波成分主要以1×，2×，3×等整数倍频为主，随着谐波次数的逐渐升高，其幅值逐渐减小。在叶冠发生双侧非对称碰撞后，偶倍频的分量明显地减弱，且奇倍频的分量相对较大，并且随着转速的增加，其偶倍频分量也是逐渐减小。当叶盘转速达到约7 000 r/min以后，由于叶片叶冠处的振动幅值小于冠间的初始间隙，以至相邻叶冠之间不能再发生碰撞摩擦。反映在三维谱振图上为转速在约7 000 r/min以后，其幅频特性均只含有气流激振力的频率成分，奇次和偶次高倍频成分均消失。

7 结论与展望

7.1 主要结论

本文讨论的是考虑振动、冲击和摩擦等因素对于航空发动机中的关键结构件——旋转叶片——动力学特性的影响。

本文的研究思路是建立关键结构件——叶片——的动力学与振动分析的多层次分析模型，包括解析模型和有限元模型，有效引入了接触、摩擦、碰撞等行为机制。

本文的研究过程是采用悬臂梁解析模型(CB-AM)及基于Euler-Bernoulli梁理论的有限元模型(EBB-FEM)，运用数值计算方法研究旋转态下叶片的固有频率；分别建立叶片-盘组合结构(BD)的梁模型(BD-BM)、机匣的梁模型(C-BM)，以及BD的质点模型(BD-PMM)和机匣的质点模型(C-PMM)，推导出叶片-机匣系统的动力学方程，利用中心差分法(central difference method)计算了叶尖与机匣之间的接触间隙；考虑叶根接触摩擦特性(CFC)，对BD的固有特性和共振特性进行分析；建立自带冠叶片(ISB)冠间碰撞摩擦的解析模型(CS-AM)与有限元模型(CS-FEM)，分析发生碰撞摩擦的叶片的振动特性。

在完成所设立的研究工作后，得到如下结论。

【研究之一】 通过对ISB的叶冠之间发生接触碰撞时的振动响应特征进行定性分析，以及对CS-AM和CS-FEM数值算例计算结果进行分析，获得以下发现。

【结论1】 叶冠之间发生单侧碰撞时，在频谱图中会出现激振力频率及其连续奇偶次倍频，且随着倍次的增加其幅值分量逐渐减小；发生双侧对称碰撞时在频谱图中会出现工频及其奇倍频，且随着奇次倍数的增加其幅值分量逐渐减小；发生双侧非对称碰撞后会出现工频及其连续奇偶次倍频，且偶次倍频分量的幅值小于相邻前一奇次倍频分量。

【Conclusion1】 Excitation frequency and its continuous odd and even multi-frequencies often appear in the spectrum of the unilateral collision between shrouds, and the amplitude component decreases gradually with the increase of time; odd multi-frequencies often appear inthe spectrum of the bilateral collision between shrouds, and the amplitude component decreases gradually with the odd time increases; continuous odd-even multi-frequencies often appear in the spectrum of the unilaterally unsymmetrical collision between shrouds, and the amplitude component of even multi-frequency is lower than that of the previously adjacent odd multi-frequency.

【研究之二】 基于CB-AM推导了考虑离心刚化效应的叶片动力学方程(Dynamic Equations Considering Centrifugal Stiffening Effect，DECCSE)，利用振型叠加法(mode superposition method)将方程离散，定性分析了叶片动频率、静频率与转频率之间数学上的平方关系，以及动频率系数的数学表达式形式；基于EBB-FEM，推导了考虑节点在y轴方向的位移和绕z轴的转角等两种自由度情况下的由离心刚化效应(CSE)导致的离心刚度矩阵(CSM)；采用CB-AM和EBB-FEM，以ANSYS为工具建立了基于Timoshenko梁理论的有限元模型(TB-FEM)，计算了一种特定形式叶片的固有频率并进行了对比。

【结论2】 叶片动频随转速的升高而增大，而且CB-AM，EBB-FEM和TB-FEM3种模型计算结果的总体变化趋势基本相同。

【Conclusion2】 Dynamic frequencies of blade increase with the increase of rotating speed, and the overall trends of results of CB-AM, EBB-FEM and TB-FEM are basically similar.

【研究之三】 建立了BD-PMM与C-PMM，并推导了PMM的质量矩阵、刚度矩阵和阻尼矩阵；给出了模态坐标与整体直角坐标下各系数矩阵之间的变换矩阵。利用Hamilton变分原理，建立了系统的统一动力学方程。通过数值算例仿真，得到了BD上每个叶片与机匣之间间隙的变化曲线。

【结论3】 在余弦模态下，轮盘上22个叶片与机匣之间的间隙是绕轮盘转动的圆周传播的两个完整波，而且不同叶片与机匣之间的间隙变化规律不相同；在余弦模态与正弦模态的共同作用下，叶尖与机匣之间的间隙变化规律基本一致，但初始相位并不相同，而且也可反映出间隙的波动波形为两个完整波。

【Conclusion3】 Under the cosine modes, varations of gaps between casing and the 22 blades are two full waves which transmit around the rotation direction of the disc, and the variational principle of each blade is distinct. Under the joint effect of cosine and sine modes, the variational principle of each blade is similar, but the initial phase is different; at the same time, the waveforms of gaps are also two full waves.

【结论4】 从第1，4，9号叶片的间隙计算结果可以看到，叶尖与机匣之间的间隙在初始间隙值附近波动，而且随着时间呈现规律性的变化，当计算出的间隙为负值时，说明叶尖与机匣已发生接触；从计算结果也可以看出行波的传播方向。

【Conclusion4】 Results of comprehensive analysis of the gap changes of the 1st, 4th, 9th blade show that the gaps between the blade-tip and the casing fluctuate in the vicinity of the initial gap value, and exhibit regularity with changes of the time. The negative gap values indicate the occurance of contact. Transmission directions of travelling waves can be observed at the same time.

【研究之四】 建立起BD-BM与C-BM，并给出了局部形函数的数学表达式。根据节径模态(nodal diameter modes)的概念，分别采用matlab对BD-BM和C-BM进行计算，同时以ANSYS为分析工具进行计算作为对比，对BD与机匣的前4节径模态进行了数值仿真。

【结论5】 通过BD-BM与C-BM得到了叶片-盘组合结构与机匣的前4节径模态， 并与ANSYS仿真得到的结果进行对比，验证了BD-BM与C-BM的可适用性。

【Conclusion5】 The first four Nodal diameter modes are obtained based on BD-BM and C-BM and compared with the result obtained by means of ANSYS，which verify the applicability of BD-BM and C-BM.

【研究之五】 考虑叶根的CFC，使用ANSYS中的面-面接触单元模拟叶根榫头与轮盘榫槽之间的接触摩擦关系，建立BD的有限元模型进行模态分析，并与将叶根视为固连的情况进行对比，分析了CFC对BD的固有特性和振动特性的影响。

【结论6】 考虑CFC与不考虑CFC时相比，可能会出现考虑CFC时得到固有频率值与振型在不考虑CFC时没有对应振型和固有频率出现等特殊情况(如表11中1 168.92Hz)。

【Conclusion6】 Natural frequencies and mode shapes obtained when considering the CFC may loss the corresponding when regardless of the CFC(such as the 1168.92Hz in Tab.11).

【结论7】 BD做节圆振动时，节圆有时会跑出轮盘，而存在于叶片处。特别是具有长叶片的轮盘，极有可能产生此种情况。

【Conclusion7】 Nodal circles of blade-disc sometimes exist at blades instead of the disc, especially when the blades are very long.

【结论8】 BD在低节径模态下振动时，轮盘对叶片的振动影响较大；随着节径数的增大，轮盘对叶片的振动影响逐渐减小，更多的表现为叶片的振动形式。

【Conclusion8】 When the number of nodal diameters is small, mode shapes of blades are susceptible to the vibration of the disc; as the number of nodal diameters increases, the influence of the disc to the blades decreases and the vibrations of blade-disc mostly occur at the blades.

【研究之六】 基于Coulomb摩擦定律和弹性体相关理论，将ISB叶冠之间的碰撞分别简化为CS-AM和CS-FEM，并分别对CS-AM和CS-FEM进行降维处理，通过数值计算方法计算了叶冠处的振动响应，利用动力学图谱分析方法阐释了ISB的振动特性。研究了叶冠间的干摩擦阻尼表面碰撞摩擦运动(surface collision friction movement of dry friction damping)的过程，应用数值仿真方法诠释了叶冠间通过碰撞摩擦耗散能量达到减振的机理。将影响叶冠振动特性的主要参数(如发动机的转速、冠间初始间隙及冠间接触弹性刚度等)引入模型，通过改变参数的数值，研究了这些参数对干摩擦阻尼减振效果的影响。

【结论9】 叶冠之间在共振转速区最容易发生接触碰撞；只有当叶片末端的弯曲振动位移大于相邻叶冠间的初始间隙时，干摩擦阻尼才能起到减振的作用。

【Conclusion9】 Contact collision between blade shrouds mostly occurs in the vicinity of resonance speed; the vibration reduction of dry friction damping is effective only when the flexural vibration displacement exceeds the initial gap between adjacent shrouds.

【结论10】 相邻叶冠间的间隙越小，振动响应的幅值越低，能更好地抑制ISB的振动。

【Conclusion10】 The smaller the gap between the adjacent shrouds, the lower the amplitude of the vibration response, i.e. the better effect of vibration reduction.

【结论11】 加大相邻叶冠间的弹性系数值，对叶片振动幅值的影响不明显。

【Conclusion11】 When elasticity coefficient values between adjacent shrouds are increased, no significant influence of blade vibration amplitude is observed.

7.2 展望

(1) 为了节省计算时间，仅采用连续型模型计算了叶片的前三阶动频，若要考察连续模型对叶片高阶动频的研究的适用性，还需对方程做高阶截断以进行更深入的计算研究。需要指出，本文建立的连续方程未能考虑叶片扭转振动对弯曲振动的影响。

(2) 基于EBB-FEM计算叶片动频时，只考虑了节点的y轴方向位移和绕z轴转动角位移等2个自由度，未考虑叶片的剪切变形。后续研究应该基于TB-FEM进行叶片分析，以考察叶片剪切变形对于叶片动频率的影响。应该指出，本文对于旋转态下叶片动频的考察，所采用的3种模型仅考虑了叶片所受离心力的影响，均未考虑科氏力和陀螺效应等因素的影响，因而需要进行更深入的工作[62]；是何问题导致3种模型计算的动频率结果有所差异，以及各个经验公式之间差异的原因，仍需做深入的探索。

(3) 对于本文所建立的CS-AM和CS-FEM，摩擦系数对叶冠之间的碰撞摩擦几乎没有影响。因而本文建立的CS-AM和CS-FEM能够很好地模拟叶冠之间的碰撞行为，而对于叶冠之间的摩擦行为，需要建立更精确的接触碰撞模型。

(4) 基于本文所采用叶片的几何尺寸和材料参数等因素，导致叶片在旋转态下的固有频率过大，如二阶动频在1 594.8～1 720 Hz，这意味着转速需达到95 688～103 200 r/min，叶片才能出现第二次共振(即在图30中，叶片振动的幅值出现第二个波峰)，这显然不现实，即使是仿真实验，在此转速下数值算法无法达到收敛。另外，本文在数值计算时，为了使计算结果更好地收敛，采用比例阻尼的阻尼系数较大，这在无意中可能丢失叶片在发生碰撞摩擦后的一些信息，因此，需要对这种强非线性动力学方程算法的适应性进行更深入的研究。

(5) 学者们针对叶冠之间的接触碰撞弹性力与阻尼力已经提出了很多模型，限于篇幅本文仅采用了其中的一种，为了比较研究各种模型的计算结果并分析其适用性，还需做进一步的研究。

(6) 本文虽然提出了叶片-盘组合结构与机匣的梁模型，但未详细提出单元质量矩阵和刚度矩阵的表达式；另外，叶尖与机匣之间的接触是强非线性接触动力学问题，叶尖与机匣间隙的计算是叶盘与机匣在各自振动节径模态下进行的，这仅是计算模型和计算方法的理论探索，具体到实际工程分析，还有待更深入地研究。

(7) 目前，国内外对先进阻尼材料在叶片减振方面的研究已经取得了一定进展，其中硬涂层用于发动机叶片的阻尼减振效果已经得到验证。涂层的施加势必会对叶片的固有特性和动力学响应特征造成一定影响，因而针对硬涂层-叶片复合结构的固有特性和动力学响应特性还需深入研究[63]。

[1] 陈予恕，张华彪．航空发动机整机动力学研究进展与展望．航空学报，2011，32(8)：1371-1391．

Chen Yushu，Zhang Huabiao．Review and Prospect on the Research of Dynamics of Complete Aero-engine Systems．Acta Aeronautica et Astronautica Sinica，2011，32(8)：1371-1391．

[2] 宋兆泓．航空发动机典型故障分析．北京：北京航空航天大学出版社，1993．

Song Zhaohong．Typical Failure Analysis of the Aero-Engine．Beijing：Beihang University Press， 1993．

[3] 华东电力试验研究所，江苏省电力试验研究所，南京工学院．汽轮机叶片的振动特性和调整．北京：电力工业出版社，1981．

East China Electric Power Test & Research Institute，Jiangsu Electric Power Test & Research Institute，Nanjing Institute of Technology．Vibration Characteristic and Adjustment of Steam Turbine Blade．Beijing：Electric Power Industry Press，1981．

[4] Murtagh P，Basu B，Broderick B．Along-Wind Response of a Wind Turbine Tower with Blade Coupling Subjected to Rotationally Sampled Wind Loading．Engineering Structures，2005，27(8)：1209-1219．

[5] Lee D，Hodges D H，Patil M J．Multi-Flexible-Body Dynamic Analysis of Horizontal Axis Wind Turbines．Wind Energy，2002，5(4)：281-300．

[6] Peters D A．An Approximate Solution for the free Vibrations of Rotating Cantilever Beams．NASA STI/Recon Technical Report，1973：1790-2011．

[7] Southwell R，Gough F．The free Transverse Vibrations of Airscrew Blades．British ARC Reports and Memoranda，1921，766：358-368．

[8] Schilhansl M．Bending Frequency of a Rotating Cantilever Beam．Journal of Applied Mechanics，1958(25)：28-30．

[9] Kuo Y H，Wu T H，Lee SY．Bending Vibrations of a Rotating non-Uniform Beam with Tip Mass and an Elastically Restrained Root．Computers & Structures，1992，42(2)：229-236．

[10] Wright A，Smith C，Thresher R，et al．Vibration Modes of Centrifugally Stiffened Beams．Journal of Applied Mechanics，1982，49(1)：197-203．

[11] Hoa S．Vibration of a Rotating Beam with Tip Mass．Journal of Sound and Vibration，1979，67(3)：369-381．

[12] Kane T，Ryan R，Banerjee A．Dynamics of a Cantilever Beam Attached to a Moving Base．Journal of Guidance，Control and Dynamics，1987，10(2)：139-151．

[13] Ho J．Direct Path Method for Flexible Multibody Spacecraft Dynamics．Journal of Spacecraft and Rockets，2012，14(2)：102-110．

[14] Hodges D H．Vibration and Response of non-Uniform Rotating Beams with Discontinuities．Journal of the American Helicopter Society，1979，24(4)：43-50．

[15] Yeh F H．Transverse Vibrations of non-Uniform Rotating Beams with Rotational and Translational Restraints．Journal of the Chinese Society of Mechanical Engineers, 1989(10)：393-400．

[16] Chung J，Yoo H．Dynamic Analysis of a Rotating Cantilever Beam by Using the Finite Element Method．Journal of Sound and Vibration，2002，249(1)：147-164．

[17] Ozgumus O O，Kaya M O．Energy Expressions and free Vibration Analysis of a Rotating Double Tapered Timoshenko Beam Featuring Bending-Torsion Coupling．International Journal of Engineering Science，2007，45(2)：562-586．

[18] Lee C，Al-Salem M，Woehrle T．Natural Frequency Measurements for Rotating Spanwise Uniform Cantilever Beams．Journal of Sound and Vibration，2001，240(5)：957-961．

[19] Banerjee J．Free Vibration of Centrifugally Stiffened Uniform and Tapered Beams Using the Dynamic Stiffness Method．Journal of Sound and Vibration，2000，233(5)：857-875．

[20] Hashemi S，Richard M．Natural Frequencies of Rotating Uniform Beams with Coriolis Effects．ASME Journal of Vibration and Acoustics，2001，123(4)：444-455．

[21] 姜广义，王德友．转子叶片和机匣的碰磨与叶片振动应力关系试验研究．航空发动机，2007(z1)：16-18．

Jiang Guangyi，Wang Deyou．Experimental Study on the Relationship Between Vibration Stress and Rub-Impact Located Among Rotor Blade and Casing．Aeroengine，2007(z1)：16-18．

[22] Muszynska A．Stability of Whirl and Whip in Rotor/Bearing Systems．Journal of Sound and Vibration，1988，127(1)：49-64．

[23] Ehrich F．Nonlinear Phenomena in Dynamic Response of Rotors in Anisotropic Mounting Systems．Journal of Mechanical Design，1995，117(B)：154-161．

[24] Legrand M, Pierre C， Peseux B. Structural Modal Interaction of a four Degree of Freedom Bladed Disk and Casing Model. Journal of Computational and Nonlinear Dynamics, 2010, 5(4): 13-41.

[25] Sinha S．Dynamic Characteristics of a Flexible Bladed-Rotor with Coulomb Damping due to Tip-Rub．Journal of Sound and Vibration，2004，273(4)：875-919．

[26] Sinha S K．Non-Linear Dynamic Response of a Rotating Radial Timoshenko Beam with Periodic Pulse Loading at the free-End．International Journal of non-Linear Mechanics，2005，40(1)：113-149．

[27] Lesaffre N, Sinou J J, Thouverez F. Contact Analysis of a Flexible Bladed-Rotor. European Journal of Mechanics-A/Solids, 2007,26(3):541-557.

[28] Lesaffre N，Sinou J J，Thouverez F．Stability Analysis of Rotating Beams Rubbing on an Elastic Circular Structure．Journal of Sound and Vibration，2007，299(4)：1005-1032．

[29] Batailly A，Legrand M，Cartraud P，et al．Assessment of Reduced Models for the Detection of Modal Interaction through Rotor Stator Contacts．Journal of Sound and Vibration，2010，329(26)：5546-5562．

[30] Legrand M，Pierre C．Numerical Investigation of Abradable Coating Wear through Plastic Constitutive Law：Application to Aircraft Engines//Proceedings of ASME IDETC/CIE 2009：1-15．

[31] Srinivasan A．Vibrations of Bladed-Disk Assemblies- a Selected Survey．ASME Journal of Vibration，Acoustics，Stress and Reliability in Design，1984，106(2)：165-168．

[32] Crawley E，Mokadam D．Stagger Angle Dependence of Inertial and Elastic Coupling in Bladed Disks．ASME Journal of Vibration，Acoustics，Stress，and Reliability in Design，1984，106(2)：181-188．

[33] Chun S B，Lee C W．Vibration Analysis of Shaft-Bladed Disk System by Using Substructure Synthesis and Assumed Modes Method．Journal of Sound and Vibration，1996，189(5)：587-608．

[34] 周传月，邹经湘．燃气轮机叶片—轮盘耦合系统振动特性计算．航空学报，2000，21(6)：545-547．

Zhou Chuanyue，Zou Jingxiang．Calculation of the Blade Disc Coupled Vibration Characteristics of a Gas Turbine．Acta Aeronautica et Astronautica Sinica，2000，21(6)：545-547．

[35] 秦 飞，陈立明．叶根尺寸误差对叶片固有频率的影响．机械工程学报，2006，42(6)：235-238．

Qin Fei，Chen Liming．Influence of Root Dimension Errors on Fundamental Frequencies of Turbine Blade．Chinese Journal of Mechanical Engineering，2006，42(6)：235-238．

[36] Gulyaev V，Khudolii S．Vibrations of Curved and Twisted Blades during Complex Rotation．International Applied Mechanics，2005，41(4)：449-454．

[37] 武新华，李卫军．自带冠叶片冠间接触碰撞减振研究．汽轮机技术，2005，47(1)：41-44．

Wu Xinhua，Li Weijun．Research on Damping of Contact or Impaction of Blades’ Tips．Turbine Technology，2005，47(1)：41-44．

[38] 徐大懋，李录平，须根发，等．自带冠叶片碰撞减振研究．电力科学与技术学报，2007，2(1)：1-6．

Xu Damao，Li Luping，Xu Genfa，et al．Research on Impact Damping of Integrally Shrouded Blades．Journal of Electric Power Science and Technology，2007，22(1)：1-6．

[39] Nagasawa S，Nagae S，Fukuzawa Y，et al．Effect of Surface Hardness of Counter Plate on Crushing of Blade Tip during Pushing Shear of Paperboard．Journal of Materials Processing Technology，2007，192(193)：265-275．

[40] 马晓峰，刘占生，侯宪科．叶片冠间接触碰撞数值模拟及实验研究．振动与冲击，2010，9(3)：34-38．

Ma Xiaofeng，Liu Zhansheng，Hou Xianke．Numerical Simulation and Experimental Research on Impact-contact Between Tips of Blades．Journal of Vibration and Shock，2010，29(3)：34-38．

[41] 李剑钊，张文平，李国镔．带冠叶片碰撞减振机理研究．热能动力工程，2009，23(6)：601-605．

Li Jianzhao，Zhang Wenping，Li Guobin．A Study of Collisional Vibration-Abatement Mechanism of Shrouded Blades．Journal of Engineering for Thermal Energy and Power，2009，23(6)：601-605．

[42] 南国防，任兴民，何尚文，等．航空发动机自带冠叶片减振特性研究．振动与冲击，2009，28(7)：135-138．

Nan Guofang，Ren Xingmin，He Shangwen，et al．Damped Vibration Characteristics of Blades with Tips of an Aero-Engine．Journal of Vibration and Shock，2009，28(7)：135-138．

[43] Pennacchi P，Chatterton S，Bachschmid N，et al．A Model to Study the Reduction of Turbine Blade Vibration Using the Snubbing Mechanism．Mechanical Systems and Signal Processing，2011，25(4)：1260-1275．

[44] Han Q，Zhai J．Multi-Level Modeling Method for Vibration Analysis of Compressor Rotating Blade//Proceedings of the 14th Asia Pacific Vibration Conference，Hong Kong Polytechnic University，2011：1314-1321．

[45] 韩清凯，于 涛，孙 伟．机械振动系统的现代动态设计与分析．北京：科学出版社，2010．

Han Qingkai，Yu Tao，Sun Wei．Modern Dynamic Design and Analysis of Mechanical Vibration System．Beijing：Science Press，2010．

[46] 韩清凯，于 涛，王德友，等．故障转子系统的非线性振动分析与诊断方法．北京：科学出版社，2010．

Han Qingkai，Yu Tao，Wang Deyou，et al．Nonlinear Vibration Analysis and Diagnosis Method of Fault Rotor System．Beijing：Science Press，2010．

[47] Wang B P，Wang J，Li X Z，et al．FE Analysis on Contact Properties between Root-Blade and Slot-Disc//Proceedings of the Advanced Engineering Forum，Trans. Tech. Publ.，2011：932-935．

[48] 《航空发动机设计手册》总编委员会．航空发动机设计手册．北京：航空工业出版社，2001．

Editor-in-Chief Committee of Aero Engine Design Manual．Aero Engine Design Manual．Beijing：Aerospace Industry Press，2001．

[49] 张 锦，刘晓平．叶轮机振动模态分析理论及数值方法．北京：国防工业出版社，2001．

Zhang Jin，Liu Xiaoping．Principle and Numerical Methods of Modal Analysis to Turbomachines．Beijing：National Defense Industry Press，2001．

[50] 任兴民，南国防，秦 洁，等．航空发动机叶片“频率转向”特性研究．西北工业大学学报，2009，27(2)：269-273．

Ren Xingmin，Nan Guofang，Qin Jie，et al．Studying Frequency Veering Characteristics of Aircraft Engine Blade with Beam Function Combination Method．Journal of Northwestern Polytechnical University，2009，27(2)：269-273．

[51] 杨文庆，孙 强，马 龙，等．某型航空发动机压气机叶片振动静频与动频的关系．空军工程大学学报，2006，6(5)：5-7．

Yang Wenqing，Sun Qiang，Ma Long，et al．The Relationship Between the Static Frequency and the Kinetic Frequency for a Certain Aero-engine Compressor Blades．Journal of Air Force Engineering University，2005，6(5)：5-7．

[52] 闻邦椿，顾家柳，夏松波，等．高等转子动力学：理论，技术与应用．北京：机械工业出版社，2000．

Wen Bangchun，Gu Jialiu，Xia Songbo，et al．Higher Rotor Dynamics—Theory，Technique and Application．Beijing：China Machine Press，2000．

[53] 刘尚明，孟繁娟．对叶片动频系数经验公式的评价．汽轮机技术，2001，43(1)：14-16．

Liu Shangming，Meng Fanjuan．The Evaluation on Empirical Formula of Blade Rotational Frequency Coefficient．Turbine Technology，2001，43(1)：14-16．

[54] Rao S S，Fah Y F．Mechanical Vibrations．London：Prentice Hall，2011．

[55] 颜云辉，谢里阳，韩清凯．结构分析中的有限单元法及其应用．沈阳：东北大学出版社，2000．

Yan Yunhui，Xie Liyang，Han Qingkai．Finite Element Method and its Application in Structure Analysis．Shenyang：Northeastern University Press，2000．

[56] 李东旭．高等结构动力学．北京：科学出版社，2010．

Li Dongxu．Advanced Structure Dynamics．Beijing：Science Press，2010．

[57] Cao D，Gong X，Wei D，et al．Nonlinear Vibration Characteristics of a Flexible Blade with Friction Damping due to Tip-Rub．Shock and Vibration，2011，18(1)：105-114．

[58] 晏砺堂，朱梓根．结构系统动力特性分析．北京：北京航空航天大学出版社，1989．

Yan Litang，Zhu Zigen．Dynamic Charateristics Analysis of Structures and Sysrems．Beijing：Beihang University Press，1989．

[59] 王春洁，宋顺广，宗 晓．压气机中叶片轮盘耦合结构振动分析．航空动力学报，2007，22(7)：1065-1068．

Wang Chunjie，Song Shunguang，Zong Xiao．Vibration Analysis of the Blade-Disc Coupled Structure of Compressor．Journal of Aerospace Power，2007，22(7)：1065-1068．

[60] Beisheim J，Sinclair G．On the three-Dimensional Finite Element Analysis of Dovetail Attachments．Journal of Turbomachinery，2003，125(2)：372-379．

[61] 胡茑庆．转子碰摩非线性行为与故障辨识的研究．长沙：国防科学技术大学出版社，2005．

Hu Niaoqing．Research on Identification of Nonlinear Behavior and Fault of Rub-impact in Rotors．Changsha：National University of Defense Technology Press，2005．

[62] Wang M L，Han Q K．The Gyroscopic Effect on Dynamic Characteristics of Dual-Disk Rotor System//Proceedings of the Advanced Engineering Forum，Trans. Tech. Publ.，2011：942-947．

[63] 王 娇，王伯平，韩清凯．压电和压磁材料硬涂层对叶片固有特性的影响．武汉理工大学学报，2011，33(8)：14-18．

Wang Jiao，Wang Boping，Han Qingkai．Contribution of Hard Coats with Piezoelectric and Piezomagnetic Effects on Natural Characteristics of Compressor Blades．Journal of Wuhan University of Technology，2011，33(8)：14-18．