基于分布式动态簇结构的WSN自适应目标跟踪算法

刘立阳，张金成，吴中林

(空军工程大学导弹学院，陕西三原713800)

在无线传感器网络的众多应用中，目标跟踪是一项基本功能。由于传感器节点体积小、价格低廉、采用无线通信方式，以及传感器网络部署随机，具有自组织性、鲁棒性和隐蔽性等特点，无线传感器网络非常适合于移动目标的跟踪。例如在战场上及时跟踪敌方车辆的行进路线和兵力的调动情况，将获取得战场信息及时发送回我方指挥中心。在多数情况下，目标跟踪系统是非线性的，粒子滤波算法由于其不受系统非线性非高斯条件的限制而被用来解决WSN的目标跟踪问题，文献［1－2］采用集中式粒子滤波的方法来解决无线传感器网络中的目标跟踪问题，取得了较高的精度。然而这种集中处理的方式由于计算复杂度较高往往难以在能量有限的单个节点上实现，所以许多学者采用分布式粒子滤波的方法来解决这一问题，文献［3－5］提出了几种采用分布式粒子滤波进行目标跟踪的方法，取得了很好的效果。

为了进一步降低算法复杂度和网络能耗，同时又要保证较高的目标跟踪精度，本文引入一种动态分簇分布式跟踪结构，提出了在目标跟踪过程中动态建簇的思想来优化目标在跟踪簇中的位置，并运用并行粒子滤波算法来提高跟踪精度，同时运用目标跟踪采样周期自适应的方式来降低网络能耗，从仿真结果来看，这种算法达到了很好的跟踪效果，同时也有效地降低了网络的能耗。

1 模型与假设

1．1 目标运动模型

目标运动模型是跟踪问题的基础，常速(constant velocity，CV)模型用于描述弱机动以及非机动的点目标状态，因此在本文的目标跟踪系统中采用CV模型作为目标的运动模型，假定目标运动基于固定速率运动，由CV模型组成的目标跟踪系统运动方程描述如下:

其中目标状态采用 CV 模型，Xk(CV)=［x，y，vx，vy］T，表示目标的状态向量，包含位置、速度，wk～N(0，Qk)表示过程噪声。Φk表示状态向量的增益矩阵，Gk表示过程噪声的增益矩阵，其中Φk以及Gk描述如下:

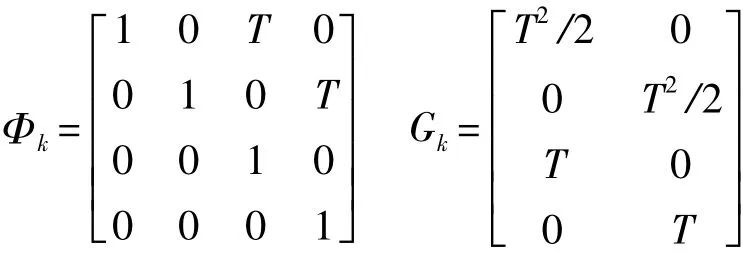
其中:T为跟踪采样周期。

1．2 传感器模型

本文假设传感器节点采集的是目标的声音信号能量，在k时刻第i个传感器节点接收到的声音能量表示如下:

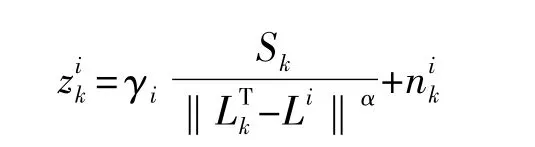
2 目标跟踪算法

2．1 分布式动态簇结构

分布式动态簇结构是由目标事件激发组建，可以根据目标事件的实时状态决定自身的位置和规模。其基本思想是:在目标跟踪过程的初始时刻，根据目标实时状态组织目标附近的一些传感器节点构成一个小规模的临时动态簇，该簇负责对目标进行状态估计，预测目标下一时刻出现的位置，当目标移动距离超过一定阈值时，由当前簇的簇头负责唤醒距离目标在下一时刻预测位置最近的节点作为新的簇头，它负责组建动态簇并进行下一时刻的目标状态估计。由于动态簇始终是由目标附近的一些传感器节点组成，因此基于动态簇的目标跟踪方法能够在维持跟踪精度的前提下降低整个网络能耗［6－7］。基于分布式动态簇结构的目标跟踪过程描述如下:

(1)当监测区域没有目标时，只有位于监测区域边缘的传感器节点处于工作状态，其它节点处于休眠状态。当有目标进入监测区域时，选取接收到目标信号能量最大的节点作为初始时刻的簇头，该簇头负责唤醒以它为中心一定范围内接收信号能量超过一定阈值的节点，被唤醒的节点接收到簇头当选信息后存储簇头的编号、坐标，调整本地时钟同步于簇头，从而构建出初始时刻的动态簇。

(2)簇头节点接收来自簇成员节点对目标的探测数据，通过粒子滤波算法估计目标在当前时刻的状态，当簇头节点到所估计的目标位置的距离超过一定的阈值(称为簇转换距离，记为D)时，进行簇的转换。此时，簇头节点通过目标运动的状态方程预测下一采样时刻的目标位置，判断目标是否离开监测区域，若离开，则停止跟踪，解散簇;否则，根据与预测位置最近且剩余能量较充足的原则，从原簇的成员节点中选择新的簇头节点。将需要传递的跟踪参数发送给新的簇头节点，同时使原簇节点进入休眠状态。

(3)当目标在下一时刻出现在预测的动态簇中时，以新簇头为融合中心，转步骤(2)。

从跟踪过程中可以看出，用于运行滤波算法的动态簇头是不断变化的，这样在不同簇头上运行的粒子滤波算法实际上是一种分布式的粒子滤波算法，在簇头转换时需要进行粒子及其权值的传递。由于直接传递粒子集会带来很大的通信代价，本文的算法中只传递通过粒子及其权值估计的均值和协方差，新的簇头节点通过近似高斯分布的采样获得粒子及其权值［8－10］。

2．2 并行粒子滤波算法

粒子滤波是基于蒙特卡罗采样的一种滤波算法，它是从后验概率分别采集带权重的粒子集，用粒子集表示后验分布，将积分转换为求和形式的一种算法［11－12］。并行粒子滤波算法的具体步骤如下:

(1)初始化。在初始时刻(k=0)，设动态分簇结构已经建立，当前簇内有M个CN(子节点)，第j个CN上分配了nj个粒子，根据先验概率p(x0|z0)进行采样，均匀分布初始粒子集，使每个粒子具有相等的权重。

(2)CN的粒子采样。在采样时刻k，已知前一采样时刻的粒子集{xi，jk－1}，通过状态方程 p(xk|xi，jk－1)预测目标状态，并采样新的粒子:

(3)CN的粒子更新和聚合。当各CN收到当前的观测量，计算粒子权重:

计算第j个CN的聚合数据:

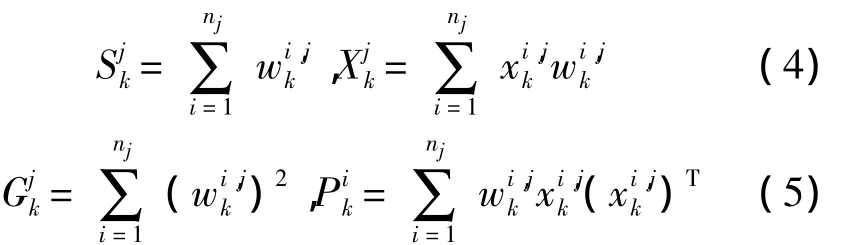
(5)在HN和CN同时进行状态估计。HN对来自CN的权重进行求和:

计算全局估计和方差，并传送到汇聚节点:

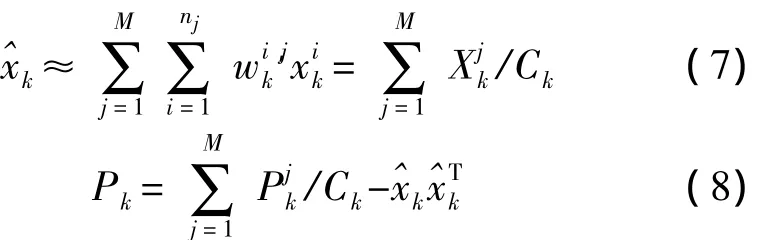
各CN接收HN的全局估计，并根据该估值计算当前目标状态:

(6)重采样。如果有效粒子数低于指定门限，则重采样粒子集。置位重采样标志f，并传送到各CN，各CN独立进行采样过程:

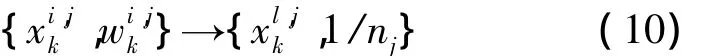
(7)粒子交换。当WSN跟踪达到分簇的临界条件，需要在新旧HN间进行粒子的传递。

2．3 跟踪采样周期自适应控制

跟踪采样周期与跟踪精度以及传感器网络能耗有着密切的关系，在传统的无线传感器网络目标跟踪算法中，跟踪采样周期往往被设定为固定值，这种方法存在着严重的弊端:如果跟踪采样周期设置过小，采样间隔变小，跟踪精度也会有所提高，但这样会造成网络能耗的增加，缩短网络寿命;如果跟踪采样周期设置过大，采样间隔变大，网络能耗大大降低，但跟踪精度也会随之下降。

由于设置跟踪采样周期为固定值会使跟踪算法的灵活性降低，所以在进行目标跟踪时，将跟踪采样周期设置为可以根据跟踪精度和网络能耗的平衡情况动态调整的参数，即在动态簇之间进行切换时，根据式(11)同时进行跟踪采样周期的调整，本文将这种方法称为ACPF(Adaptive Cycle Particle Filter)算法。

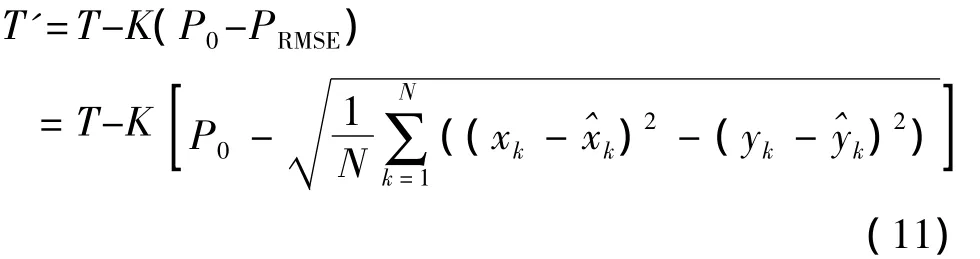
其中，T为上一动态簇采用的跟踪采样周期，T'为下一动态簇要采用的跟踪采样周期，K为增益常数，P0为预设的目标位置均方根误差允许值，PRMSE为动态簇从建立到解散过程中目标位置的均方根误差统计值。

3 仿真实验及结果分析

为了验证基于动态簇结构的分布式粒子滤波算法在在无线传感器网络中对目标的跟踪效果，本文进行了响应算法的仿真实验。仿真实验主要从跟踪精度和网络能耗两个方面来考察算法的性能，其中跟踪精度用目标位置估计得均方根误差(RMSE)来描述，网络能耗用每一时刻激活的节点数量来描述。仿真初始条件设置如下:①WSN仿真环境由20个传感器节点组成，传感器节点随机布置在坐标(0，0)和(500，500)之间。②每个传感器建模为被动传感器，通过预先建立的传感器模型观测目标的距离信息，有效观测距离R=200 m，节点间最大单跳通信距离为r=50 m。③仿真目标执行常加速和转弯机动运动，目标的初始运动参数 x0=［0，0，10，6］。④观测噪声为零均值的高斯白噪声，标准差选择为0．5m。⑤粒子数为N=100，仿真跟踪时间为100 s，观测量初始采样间隔T=1 s。

图1为采用PF算法以及本文所提出的ACPF算法所描述的轨迹与目标真实轨迹的对比图，由图1可以看出，PF算法与ACPF算法都有较好的跟踪效果，但ACPF算法由于采用了跟踪采样周期自适应的控制方式，能够根据跟踪的精度自适应地调整跟踪周期，使得跟踪精度始终保持在一个较小的范围内变化，所以其估计轨迹的起伏性比PF算法要小。

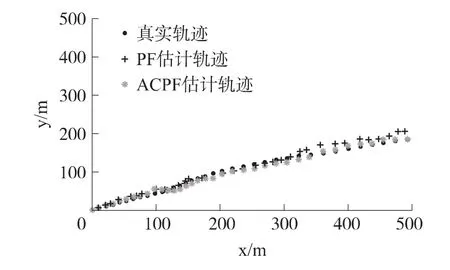
图1 轨迹跟踪对比图

图2为两种算法下的目标位置均方根误差(RMSE)的对比图，由图2可以看出，ACPF算法的RMSE明显小于PF算法的RMSE，说明ACPF的跟踪精度较高。

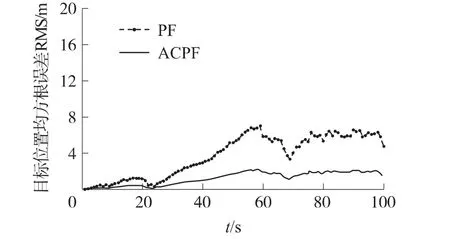
图2 目标位置RMSE对比图

图3比较了PF和ACPF算法所需的通信数据量，它可以反映不同算法下的网络能耗［13－14］，由图3可以看出，尽管簇头的选举和簇头间的粒子交换都产生了一定的通信消耗，但可以看到ACPF算法的平均通信量要低于PF算法，所以ACPF算法是更优的WSN分布式跟踪算法。

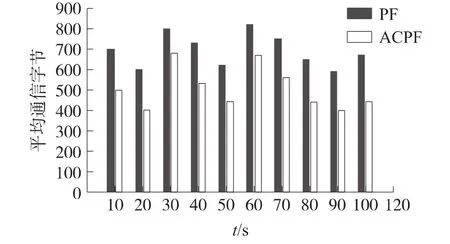
图3 平均通信数据量对比图

4 结论

在无线传感器网络中，由于传感器节点能量有限、且部署随机，要实现对目标较高精度的跟踪是非常有挑战性的任务。为了进一步提高目标跟踪精度，同时尽可能降低网络能耗，本文将并行粒子滤波算法与分布式动态簇结构相结合，提出了跟踪采样周期自适应的ACPF算法。仿真结果表明，本文提出的算法具有较好的跟踪效果，并且通过自适应地调整动态簇的跟踪采样周期，在保证跟踪精度的条件下降低了整个网络的能耗，对实际应用具有重要的指导意义。

［1］ Djuric P M，Vemula M，Bugallo M F．Signal Processing by Particle Filtering for Binary Sensor Networks［C］//Proc．of the IEEE 11th Digital Signal Processing Workshop＆IEEE Signal Processing Education Workshop，2004:263－267．

［2］ Djuric P M，Vemula M，Bugallo M F．Target Tracking by Particle Filtering in Binary Sensor Networks［J］．IEEE Trans．on Signal Processing，2008，56(6):2229－2237．

［3］ Chen W，Hou J C．Dynamic Clustering for Acoustic Target tracking in Wireless Sensor Networks［C］//Proc．of the I EEE 11th International Conference on Network Protocols，2003:284－294．

［4］ 邓克波，刘中．基于无线传感器网络动态簇的目标跟踪［J］．兵工学报，2008，29(10):1197－1202．

［5］ 薛锋，刘忠，曲毅．无线传感器网络中的分布式目标被动跟踪研究［J］．系统仿真学报，2007，19(15):3499－3502．

［6］ Djuric P M，Vemula M，Bugallo M F．Target Tracking by Particle Filtering in Binary Sensor Networks［J］．IEEE Trans．on Signal Processing，2008，56(6):2229－2237．

［7］ 黄艳，梁韦华，于海斌．基于粒子滤波的无线传感器网络目标跟踪算法［J］．控制与决策，2008，23(12):1389－1393．

［8］ Viani F．Object Tracking Through RSSI Measurements in Wireless Sensor Networks［J］．Elect ronics Letters，2008 44(10):653－654．

［9］ 章坚武，张潞，应瑛，等．基于ZigBee的RSSI测距研究［J］．传感技术学报，2009，22(2):285－288．

［10］ Oka A，Lampe L．Energy Efficient Distributed Filtering with Wireless SensorNetworks［J］．SignalProcessing，IEEE Transactionson Acoustics，Speech，and Signal Processing，2008，56(5):2062－2075．

［11］李迅，李洪峻．基于簇结构的无线传感器网络移动目标精确跟踪［J］．传感技术学报，2009，22(12):1813－1817．

［12］ Liu Juan，Chu Maurice，James E Reich．Multitarget Tracking in Distributed SensorNetworks［J］．IEEE SignalProcessing Magazine，2007:36－47．

［13］ CelebiM B，Kara A，Akar B．A New App Roach to Threat Tracking on ESM Systems by Using Kalman Filters［C］//Signal Processing and Communications Applications Conference，2009．SIU．2009．IEEE 17 th 9－11 April 2009:173－176．

［14］ Yang Weon Lee．Development of the Multi-Target Tracking Scheme Using Particle Filter［C］//ISNN 2007，PartⅢ，LNCS 4493:1192－1201．