基于多传感器数据融合的机器人里程计设计与实现

余 翀，高 翔，邱其文

(1．复旦大学信息科学与工程学院，上海200433;2．南京邮电大学自动化学院，南京210046)

在智能空间［1－2］中，机器人依据指令到达指定地点完成任务，需要一个精确的定位系统作为保证。在机器人定位技术［3］中有两类常用方法:航距推算法［4］和三角测量法［5］。其中航距推算法是一种直接进行移动机器人定位的方式，它不依赖外部参照，主要靠机器人自身携带的里程计完成到出发点的距离计量，故应用广泛。常用的里程计有光电编码器、加速度计等，但它们存在两个主要问题。一是里程计测量距离的准确程度与车体自身运动情况有关，是一种相对测量结果;二是受传感器自身精度、环境噪声和人为干扰等因素的影响，单一的里程计结果具有不确定性。

本文结合应用场景及实际需求，设计实现了一种基于FPGA和多光电鼠标的高精度机器人里程计，该里程计可以很好的解决以上两个缺陷。首先利用光电鼠标传感器自身特性［6］，使得里程计工作不依赖于车体自身运动情况，得到绝对测量结果。其次在研究多传感器数据融合算法［7］的基础上，用FPGA硬件实现，将来自多个光电鼠标里程计的信息进行综合处理［8］，得出比单一里程计更为准确可靠的结论。本文将详细介绍该里程计设计方案及实现。

1 光电里程计

1．1 PS/2光电鼠标传感器

PS/2协议与设备接口是由IBM公司开发、使用，并最早出现在IBM技术参考手册里。物理上，PS/2端口连接器有两种:一种是5脚的DIN，另一种是6脚的mini-DIN。本文设计实现的机器人里程计所选用光电鼠标PS/2接头是6脚的mini-DIN规格，表1给出了六脚标准的引脚定义，表2给出了PS/2协议通讯数据帧格式，图1为通讯时序图。

表1 6-pin Mini-DIN(PS/2)连接器引脚定义

表2 PS/2设备到主机的通讯过程中数据帧中各个位含义

图1 PS/2设备到主机的通讯时序

标准的PS/2鼠标支持如下的输入信号:X(左右)方向的位移大小，Y(上下)方向的位移大小，左键状态，中键状态和右键状态。鼠标以一个固定的频率读取这些输入信号，并更新各种计数器和标志位，以反映出位移大小和按键所处状态。表3给出了鼠标数据包格式。本文应用光电鼠标传感器做机器人里程计，故只用到其数据包中的Byte 2、Byte 3及Byte 1中相应的状态位。

表3 PS/2数据包格式

本论文所选用光电鼠标，其分辩率达800 DIP，数据刷新频率为100 Hz。所设计的机器人里程计由传感器支架和六个经改造过的光电鼠标传感器构成，六个光电鼠标数据同时按PS/2协议与FPAG通讯，并在FPGA中进行6个光电鼠标的数据融合操作，得到融合出的光电鼠标里程计最终结果。

1．2 FPGA处理单元

在本论文设计的光电鼠标里程计中，FPGA上电初始化光电鼠标，使其进行到默认的Stream模式，而不对鼠标进行控制和操作，所以在里程计工作过程中，FPGA只需被动的读取来自光电鼠标的数据包，并把数据包中的X、Y位移量提取出来便完成数据通讯，也就是说系统中只涉及PS/2设备到主机的通讯过程。

当PS/2设备上传数据给主机时，它们首先检查时钟信号，以确保时钟信号是高电平状态，否则表明主机抑制了数据通讯，那么设备须缓冲待上传数据。PS/2鼠标是在检测到位移量发生变化或发现有一个或多个鼠标键的状态发生变化时触发数据包传送动作。

在光电鼠标里程计系统中FPGA-EP2C8Q208C 8N负责解析PS/2协议并读取PS/2鼠标数据包，然后在芯片内完成六个光电鼠标数据融合操作。系统结构如图2所示。

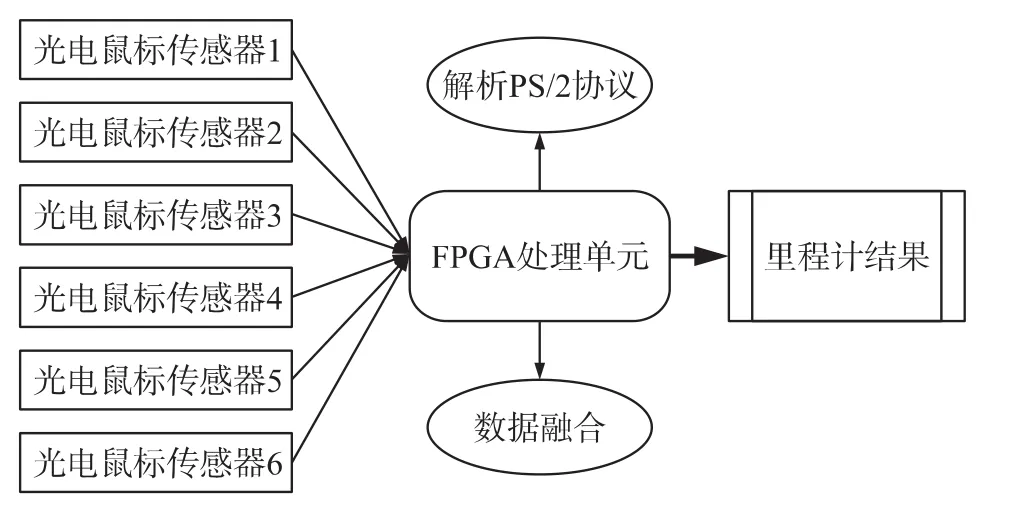
图2 光电里程计系统结构

2 多传感器数据融合算法

2．1 数据融合背景

实际控制系统为了与周围环境发生交互，必须有相应的系统去检测周围环境状态［9］。在机器人的控制系统中，检测系统还担负着机器人在环境中定位的任务，所以检测系统成为控制系统与周围环境交互沟通的桥梁。为了使检测到的数据更精确，更有参考价值，我们需要用多种传感器来构成检测系统［10］。

在实际环境中，多传感器检测系统受到各种传感器自身的精度、环境噪声和人为干扰等因素的影响，使得系统测得的数据具有不确定性，相当于在真值上叠加了随机噪声。我们希望通过一定的算法和硬件电路的实现，将各传感器实际测得的不确定数据综合处理，完成多传感器的数据融合，得出比单独一个传感器或是单独一类传感器更为准确、确定、可靠的信息和结论。

2．2 一致性数据融合算法

由n个传感器组成的检测系统，各传感器从不同位置相互独立地对某一目标参数μ进行测量，设第i个传感器测得的数据为xi，它服从正态分布。其中是对该传感器测量值偏离真值μ的一种度量，σi表示第i个传感器的测量精度，则传感器测量模型可用高斯概率密度函数表示为:

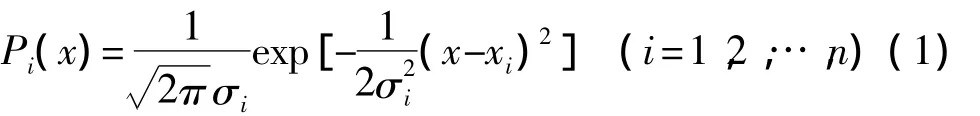
为了检验传感器测量的一致性，定义置信距离测度 dij和 dji:

当i≠j，且第i个传感器与第j个传感器的测量精度不同时，置信距离一般不等于，而通常置信距离的定义要求满足对称性，即，这是经典的Luo一致性数据融合方法［11］一个不足之处。为了克服因为各个传感器测量精度不同而导致的置信距离的不一致，现对置信距离做如下定义:

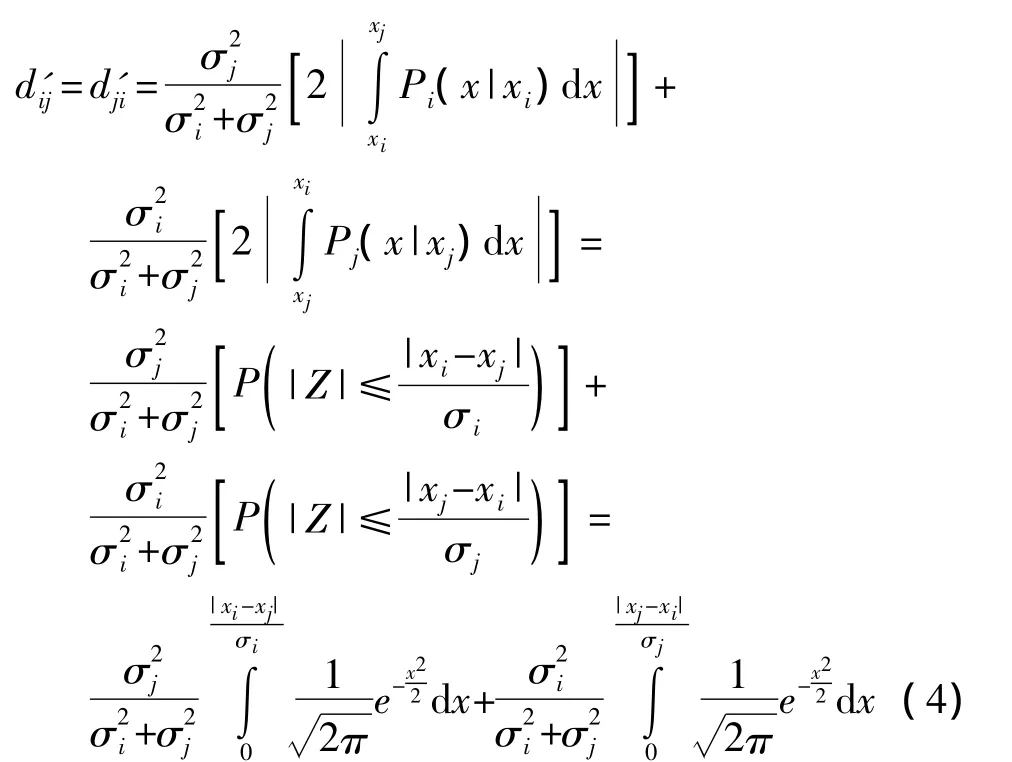
根据物理实际，测量精度低的传感器所测得的数据，其方差σ2较大，而测量精度高的传感器所测得的数据，其方差σ2较小。由式(4)可见，测量精度低的传感器所测得的数据被赋予了较小的权重，而测量精度高的传感器所测得的数据被赋予了较大的权重。因此，通过权重大小的不同来反映和补偿因各传感器测量精度的差异而对置信距离产生的影响，其物理意义明确。

当n个传感器同时测量某一物体特征时，各传感器之间的置信距离测度构成一个矩阵Dn，称为置信距离矩阵。

置信距离矩阵描述了各传感器间的一致性支持程度，根据该矩阵可以确定一个传感器对另一个传感器的支持关系。

在经典的Luo一致性数据融合方法中，第i个传感器对第j个传感器支持程度指标rij一般是由带有经验性的置信距离阈值εij决定的，具有很大的主观性，阈值选取不当，就可能会对结果产生很大的影响。并且rij要么取0，要么取1，当测量数据发生扰动时，可能会加大数据融合结果的误差［12］。作为改进，在本算法中rij应结合各个传感器的相互支持程度情况，取值是模糊而非绝对的。从实际物理意义上来说，置信距离dij越是接近于经验阈值εij，则此距离所涉及的第i个传感器对第j个传感器支持与否结论越为模糊;而只有置信距离dij越远离经验阈值εij，才能越清晰的说明第i个传感器对第j个传感器的支持程度。同时，置信距离dij在阀值εij附近存在模糊，但是随着置信距离dij增大，这种模糊性将很快消除，所以用二次曲线可以很好地表示这种模糊性。利用椭圆曲线将传感器测量数据之间的相互支持程度大小rij定义为:

在置信距离阈值εij的作用下，由置信距离矩阵Dn，可以得到传感器之间的关系矩阵(又称为支持矩阵)Rn

关系矩阵(支持矩阵)Rn可以量化出各个传感器的测量数据被其他传感器测量数据支持的程度。

2．3 多传感器数据融合

在支持矩阵Rn中，rij仅表示2个传感器的测量值xi和xj之间的相互支持程度，并不能反映第i个传感器测量值xi，被系统中所有传感器测量值的综合支持程度［13］。

设βi表示第i个传感器测量值xi被所有传感器测量值的综合支持程度，βi数值越大，表明xi被其他测量值支持的程度越高，即在数据融合中的重要程度越高。根据信息分享原理，最优融合估计的信息量之和可等效分解成若干信息量之和，或者说一个信息可被若干个子系统所分享，且各信息所具有的权系数应满足

根据概率源合并理论，存在一组非负数p1，p2，…，pn，使得

将式(9)写成矩阵形式，则有

式中:β=(β1，β2，…，βn)T，P=(p1，p2，…，pn)T。

支持矩阵Rn是一个非负对称矩阵，由Perron-Frobenius定理可知，Rn存在最大模特征值λ(λ＞0)，使得该特征值λ对应的特征向量

为正，并满足下式:

那么λY可以作为测量数据的综合支持程度的度量，则第k个传感器的综合支持程度可以通过矩阵展开得到:

比较式(9)和式(12)，可知P即为Y归一化后的结果，故令:

则αk为第k个传感器的综合支持程度，利用α1，α2，…，αn，可以给出多传感器的最终数据融合值为:

3 实验研究

由于实际应用场景中6个光电鼠标传感器两两夹角为60°，直接测量所得数据没有相互可比性，所以首先在直角坐标系中对每个光电鼠标测得的位移数据做预处理。取10组处理后的典型数据(其中有1个光电鼠标传感器测量值有较大误差)来测试传感器数据融合算法的效果，实验数据如表4所示。

表4 6个光电鼠标传感器预处理后的测量值和数据融合结果 单位:mm

为了便于比较，采用简单平均法对6个光电鼠标传感器测得数据进行处理，将10组目标真值、算术平均值和多传感器数据融合结果用图3表示。

图3 目标真值、算术平均值与多传感器数据融合结果比较

由于光电鼠标传感器精度高，所以当各光电鼠标传感器测量准确时，采用本文的多传感器数据融合算法得到的数据融合结果和简单算术平均数，都很接近于目标真值。而当某些个光电鼠标传感器测量含有较大误差或测量错误时，通过分析上图中三条折线可知:采用本文的多传感器数据融合算法得到的数据融合结果，比简单算术平均数更加接近于目标真值，可以大大降低这些异常数据的干扰。

根据常用的数据处理方法，在对测量结果取算术平均值时，应当先剔除有较大误差的数据结果，即通过设定一个阈值，将和其他数据传感器测量结果相差较大的结果去掉。但是作为应用在机器人定位系统上的里程计，其测量结果依赖于机器人的运动状态。因此在机器人运动状态快速变化的情况下，无法通过设定阈值的方式来剔除异常数据的干扰。此时采用本文的多传感器数据融合算法，在不剔除这些异常数据时，数据融合结果仍然能够达到较高的测量精度要求。

4 结论

机器人的精确定位是为实现智能空间中机器人提供相应服务的前提，而机器人里程计是实现机器人定位技术的核心。本文在前人研究基础上，改进了经典的Luo一致性数据融合算法，设计实现了多传感器数据融合算法。该算法计算步骤固定，方便在FPGA上实现，在此基础上，利用PS/2光电鼠标传感器，设计实现了一种高精度机器人里程计，可以应用于各种机器人系统中。

［1］ Reetz Eike S，Tonjes Ralf，Baker Nigel．Towards Global Smart Spaces:Merge Wireless Sensor Networks into Context-Aware Systems［C］//5th IEEE International Symposium on Wireless Pervasive Computing(ISWPC)，Modena，Italy:IEEE，2010:337－342．

［2］ Blum N，Yamada J，Fukayama A，et al．A Smart Information Sharing Architecture in a Multi-Access Network，Multi-Service Environment［C］//International Conference on Communications(ICC)，Kyoto，Japan:IEEE，2011:1－6．

［3］ Ruiz D，Urena J，Garcia J C，et al．Sim-Ultaneous Mobile Robot Positioning and LPS Self-Calibration in a Smart Space［C］//International Symposium on Industrial Electronics(ISIE)，Henares，Spain:IEEE，2010:2865－2870．

［4］ 白亮，秦永元，成研．基于序贯处理的航位推算组合导航算法研究［J］．传感技术学报，2010，23(5):687－690．

［5］ 王忠巍，曹其新，栾楠，等．基于多传感器数据融合的管道机器人精确定位技术［J］．机器人，2008，30(3):238－241．

［6］ Kim S，Lee S．Roubust Mobile Robot Velocity Estimation Using Redundant Number of Optical Mice［C］//Information and Automation，2008．ICIA 2008．International Conference on，June 2008，107－112．

［7］ Xu Shu-sheng，Lin Xiao-gong．Asynchronous Multi-Sensor Hierarchical Adaptive Data Fusion Algorithm［C］//International Conference on Complex Medical Engineering(CME)，Harbin，China:IEEE/ICME，2011:285－288．

［8］ 万树平．运用距离测度进行多传感器目标级信息融合［J］．计算机工程与与应用，2010，46(18):128－129．

［9］ 薛晗，李迅，马宏绪．基于无线传感器网络的移动机器人智能导航算法［J］．传感技术学报，2008，21(5):834－840．

［10］ Kermorgant Olivier，Chaumette Francois．Multi-Sensor Data Fusion in Sensor-Based Control:Application to Multi-Camera Visual Servoing［C］//International Conference on Robotics and Automation(ICRA)，Beaulieu，France:IEEE，2011:4518－4523．

［11］ Lou R C，Lin M，Scherp P S．Dynamic Multi-Sensor Data Fusion Systemfor Intelligent Robots［J］．IEEE Journal of Robotics and Automation，1988，4(4):386－396．

［12］ Jin Tae-Seok，Lee Jang Myung，Tso S K．A New Approach Using Sensor Data Fusion for Mobile Robot Navigation［J］．Robotica，2004，22:52－59．

［13］ George，Jemin，Kaplan，et al．Multi-Sensor Data Fusion:An Unscented Least Squares Approach［C］//Proceedings of the 14th International Conference on Information Fusion(FUSION)，Chicago，IL，USA:IEEE，2011:1－8．