断砖可为玉 点石能成金

　　摘 要：数学教学活动常常通过矛盾冲突来唤起学生的内在需求，激发学生的参与意识，推进新知的探究进程。教学中教师可以依据学情，恰当使用策略，在情境中用冲突点燃激情，在旧知铺垫中用冲突有效对接，在引导操作中用冲突感悟算理，在比较思辨中用冲突明确本质，在巩固练习中用冲突深挖内涵，以此来丰满学生认知建构的过程，点亮数学探究的旅程，让数学课堂焕发出迷人魅力。
　　关键词：小学数学；认知冲突；引发探究
　　中图分类号：G623.5 文献标识码：A 文章编号：1009-010X（2011）06-0046-03
　　
　　所谓认知冲突，是指学生已有的认知结构与当前学习情境之间存在的暂时性矛盾，通常表现为学生已有的知识和经验与新知之间存在某种差距而导致的心理失衡。这个矛盾如同拦在学生学习道路上的“砖头”和“石块”，会给学生一定的干扰。但这种失衡又能促进学生不断地追求新的平衡而完善认知。因此，教学中巧妙设置并科学处理这些“砖头”和“石块”尤为重要。戏剧是通过激烈的矛盾冲突来塑造人物形象、反映社会生活。教学可以通过矛盾冲突来唤起学生内在需求，激发参与意识，推进探究进程，使数学课堂起伏跌宕、摇曳多姿，呈现出迷人的艺术魅力。
　　
　　一、借用情境，诱发冲突，点燃激情
　　
　　教学中，教师可根据既定的教学目标创设合适情境，将学生生活实际或经验与新知进行联接，让情境能更好地为教学服务。因此，教师可以在情境中巧妙设伏，激发学生认知冲突，造成心理悬念，唤起探究欲望，使学习目标更明确。
　　如教学“圆的认识”时，教师先创设情境：有8位同学排成如下队形玩定点投篮游戏（如右图），你会选择什么位置？根据所站位置与篮筐的距离，学生会选择②④⑤⑦。教师接着问，为什么？您能设计一种对8位甚至更多的同学都比较公平的队形吗？
　　因学生不能用学过的长方形、正方形、三角形等知识来解决情境中所提出的问题，所以产生了认知冲突——现有队形对于游戏不公平，点燃了学生的探究激情，同时也为进一步的认识圆埋下伏笔：怎样才能使这8位同学站成圆形？篮筐的位置如何确定？人与篮筐的距离为什么是相等的？这样，从开始的情境创设再辐射到探究的整个过程，既诱发了学生的探究兴趣，又让学生带着更多的问题进行更深的探究，凸显了探究目标的明确性。
　　
　　二、旧知为媒，引发冲突，促进探究
　　
　　知识如同大树，新知乃是“新枝”。如在“新枝”生长点处引发冲突，学生对新知会掌握得更牢。教师可以通过分析学生已有的知识结构、经验和教材内容，利用新旧知识的差异，发掘“结合点”，引发认识冲突，促进学生探究。
　　
　　如教学“1格表示多个单位的条形统计图”，教师以学生已有的知识为媒介，有效地制造思维冲突，引领学生自己发现问题，提出解决问题的方案。首先用表格出示国际展览局投票确定2010年世博会举办地时其中3个申办城市的得票情况：波兰佛罗茨瓦夫2票，俄罗斯莫斯科12票，墨西哥克雷瓦罗6票，让学生在方格图上用直条表示，复习“1格表示1个单位”；接着继续添加韩国丽水28票、中国上海36票，让学生继续补充统计图，引发冲突——方格图上最多只有14格，丽水和上海得票数无法表示。教师及时引导学生讨论交流，得出：可以增加方格图的行数，也可以用1格表示2票或者更多的票数，并让学生对比，哪种表示方法更好一些。
　　学生是学习的主人，我们必须让他们面对认知冲突，为他们创设一个个探究阶梯，引领他们对旧知进行充分的思维加工、深化和发展，促进新知的形成。
　　
　　三、动手操作，酝酿冲突，感悟算理
　　
　　学习数学，学生通常是从感知具体事物中获得感性认识开始的。积极引导学生进行操作是获得感性认识的主要途径。在操作过程中产生一些认知冲突，让学生的操作显得更加有意义，增强学生操作的探究性和趣味性，促进学生动手动脑，开拓思维。
　　如教学“长方形的面积”，教师先让学生用12个边长为1cm的小正方形纸片摆出不同的长方形，并说出长方形的面积，得出：求一个长方形的面积，可以用边长为1cm的正方形摆一摆，能摆满多少个小正方形，面积就是多少平方厘米。教师接着让学生用手中的12个小正方形去量一量长为5cm，宽为4cm的长方形，从而产生冲突：小正方形不够，该怎么办？经过一番思考与操作，学生用了以下办法：
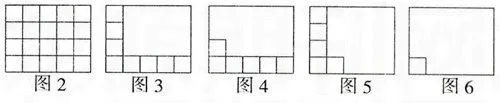
　　生1：可以用摆过的正方形再移一移，就行了（如图2）。
　　生2：我只要8个小正方形就可以量出来了（如图3）。
　　教师进一步引导：能不能再少一些正方形呢？课堂顿时再起波澜，学生兴趣盎然，积极动手。
　　生3：用6个小正方形就行了，用5个量出长，用1个去量宽（如图4）。
　　生4：用5个也行，先用4个量出宽，用1个去量长（如图5）。
　　生5：我只用1个小正方形就可以了，先用它去量长，量5次，再用它去量宽，量4次，说明摆20个小正方形。（如图6）。
　　
　　教师在关注学生探求知识过程和方法的同时，注重了从直观感知到初步尝试的运用，并适当设置冲突，放大困难，激励学生在正方形个数不够的条件下，充分激活学生的思维，完成了似乎看起来完成不了的操作任务，并悄然建立了长方形面积计算公式模型。小正方形个数从20到12、8、6、5，最后到1个，从数面积单位到用面积单位去量，从用面积单位去量到用长方形的长乘宽，使数学思维的抽象美、数学公式的凝练美、数学方法的简约美展现得淋漓尽致。
　　
　　四、巧破平衡，暗伏冲突，深化思维
　　
　　学生接受新知，应是一个不断完善、不断深化的过程。在学生还没有完全掌握新知时，往往会出现认知上的一些盲点。此时，如果适当设置陷阱，引诱学生落入其中，再将学生从中“救起”或引导学生进行“自救”，有助于学生对新知进行深度地反思和提炼，达到完美建构。
　　教学“三角形的稳定性”，许多教师通过拉三角形框架的演示加以说明。这样做，确实可以给学生展示“它是什么”，却忽视了“它为什么是这样的”。那么，三角形为什么具有稳定性呢？我先通过自行车架、空调支架等说明三角形稳定性的应用，再让学生拉一拉三角形和平行四边形的框架，得出结论，平行四边形容易变形，三角形不易变形。但教师并不就此收场，继续设疑：三角形为什么具有稳定性呢？首先出示了用塑料吸管围成的三角形，让学生试着拉一拉，发现有一些细微的变形。此时教室里出现了一些躁动，学生刚建立的认知顿时又失去了平衡。教师接着让学生用小棒摆出一个三角形，并问，还用这些小棒，能不能摆出不同的三角形呢？学生通过操作和观察发现，只能摆出一个三角形。教师继续引导，如果用4根小棒能摆出几个四边形？学生通过操作发现能摆出多个不同形状的四边形。此时，三角形的稳定性不说自明。
　　从认识三角形的稳定性到为什么具有稳定性，教师没有让学生“一跃而过”，而是通过拉动塑料吸管三角形，打破了认知平衡，产生了新的冲突，引发了学生的深度思考，由浅入深、由表及里地开展探究活动，让学生的认知更加深刻。
　　
　　五、比较思辨，开掘冲突，明确本质
　　
　　教育家乌申斯基指出：“比较是一切理解和思维的基础。”比较可让学生在识同辨异的过程中进行抽象和概括，深刻认识事物属性，明确把握事物本质。在新知初步形成之际，教师适当引入比较策略，形成认知冲突，再通过鲜明的启发，防止知识的混淆，提高辨别能力。
　　如“倍的认识”的教学，教师通过圈一圈的办法使学生初步形成“倍”的表象，再提供反例，让学生在比较思辨中加深理解：让学生观察下图（图7），这里的苹果的个数是梨的3倍还是2倍？
　　
　　
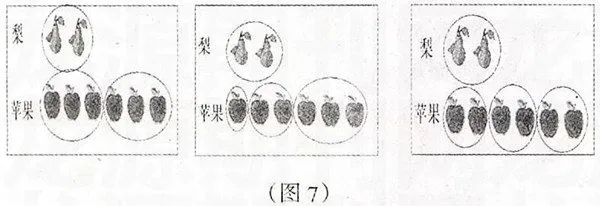
　　有的学生认为第一幅图圈得对，苹果数是梨的2倍，因为每一个圈内苹果一样多；有的认为第二幅图是对的，这里的苹果有2个为一圈的，梨的个数是苹果的3倍。面对学生的冲突和迷茫，教师明确引导：第一幅图中圈内梨的个数是2，而圈内的苹果数是3，第二幅图苹果虽然有2个为一份的，但也有1个和3个为一份的。学生经过讨论与交流达成共识：要根据梨子的数目来圈苹果，而且每一个圈内的苹果数要与梨子的数目相等，彼此之间也应该是相等的，所以正确的圈法应该是第三幅图。
　　上述教学，教师通过变换事物的本质属性来引发认知冲突，并在比较思辨中帮助学生从反省中引起对新学知识更为深刻的正面思考：圈内的苹果的数目并不是随意的，一是要根据梨的个数（每份数）来圈，二是要兼顾到每个圈内的数量是相同的。典型反例的恰当介入，认知冲突则立即形成，“倍”的内涵就是这样在思辨中得到强化。
　　
　　六、挖掘隐含，迸发冲突，再度拓展
　　
　　让学生进行适当的练习可以巩固新知，增强能力。虽然练习题中的已知条件对于解题思路具有鲜明性、导向性，其实显性的条件背后往往有着更为深刻的隐含，问题中会有新的问题。教师可以利用隐含条件，形成认知冲突，激发学生发现和探究新问题，让其穿越“山穷水复疑无路”的迷茫，享受“柳暗花明又一村”的畅快。
　　如在“圆的面积”巩固练习中，教师设计练习：物业管理处准备在小区一块长24米、宽18米的长方形花坛内任意修建一个直径为4米的圆形水池，水池外围的花坛平均分成两部分分别栽上两种不同的花卉。问每种花卉的占地面积是多少？
　　教师发现不少学生是借助平面图来帮助解题的，大都是在长方形内正中央画一个圆，通过对角线或对折线来对外围图形进行平均分。教师感觉圆的位置与题中“任意”二字不太相符，于是指出，这个圆一定要画在正中央吗？问题一抛出，学生再次尝试画图后都认为，圆如果不在中央就不能把圆外的部分平均分成两份，应该把题中“任意”改成“中间”更适合。教师不置可否，只是先让学生采取尽可能多的方法用直线把长方形平均分成两份（如图8），从中发现只要是经过长方形中心点的直线都可以把它平均分成两份，再用相同的方法把圆平均分成两份，得出只要是经过圆心的直线都可以把它平均分成两份的相同结论（如图9）。接着教师让学生分组探究，发现“能同时经过长方形和圆的中心点的直线就可以将这个图形平均分成两份，而且这样的直线只有一条”这一规律（如图10）。
　　
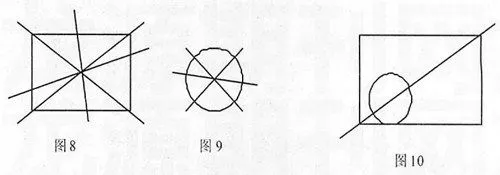
　　教师紧扣“任意”二字，极具慧眼地挖掘出练习题条件中隐含的内容，并适时设置冲突，引领学生把探究的眼光延伸到练习题本身以外，使其在经历图形的动态变换过程中，丰富数学思想，改进数学方法，拓宽数学视野，发展数学思维。
　　应该说，教学是一种矛盾冲突的艺术。制造冲突既是教学艺术的灵魂和精髓，又是提高学生思维能力的原动力。在以学生的自主探索为主旋律的数学课堂上，教师关注学生探究参与的程度，注重学生知识获取的过程，自然不能忽视认知上的冲突对促进学生有效学习起到的不可低估的作用。