在“做数学”的过程中学习数学

　　“听过了，就忘记了；看过了，就明白了；做过了，就理解了。” 课改以来，这三句话已成为广大教师进行教学方式改革的座右铭。为什么呢？是因为现代教育心理研究表明：人们在学习时，如果仅靠听和看最多能吸收30％的新知，如果动手做的话，可以达到90％以上。因此，在教学中根据学生实际、教学内容、现有教学条件营造一种有吸引力的学习背景，让学生协调多种感官（眼、耳、手、脑）“做”数学，经历数学知识的发生、发展和形成过程，逐步获得一般的数学思想方法，感受数学创造的乐趣，促进学生全面、持续、和谐地发展，已成为课程改革的主要目标。
　　一、让学生在“做数学”中掌握数学概念
　　1. 经历概念的形成过程
　　概念是思维的细胞，数学知识是以概念为基础的。一般的数学概念，都是通过对研究对象或某些具体的事例进行分析，经过抽象概括而导出的，它有一个形成过程。要使学生获得扎实稳固的基础知识和基本技能，就必须让其掌握清晰准确的数学概念。要达此目的，就要尽可能地创造条件，使学生在做数学的过程中经历概念的形成过程。
　　如，教学《分数的初步认识》时，为了让学生理解分数这个抽象的概念，我设计了一系列不同层次的折纸活动。
　　第一次我让学生在一个长方形中折出1/2，并把它的1/2涂上颜色。全班反馈，共有3种不同的折法（主要是横、竖对中折和对角线折）。在学生展示自己的折法后，我问：大家折法不同，为什么涂色的部分都是长方形的1/2呢？ 生1：因为我们折的都是一半。生2：都是把长方形平均分成2份，涂色的是其中的一份，表示1/2。通过比较和分析，学生发现折法不同没关系，只要折的是这个长方形的一半，则每一份都是它的1/2。
　　第二次我让学生在事先准备好的长方形、正方形、圆形中折出1/4。当学生展示折的结果，即长方形、正方形、圆形的1/4 后，我问：这些图形的形状不同，为什么涂色部分都是它的1/4？生：因为它们都平均分成了四份，涂色的是其中的一份，表示1/4。通过活动学生发现，不同的图形能用相同的分数表示。
　　第三次活动前，我先让学生想象一下用大小相同的圆，分别折出它的1/2 、1/4和1/8，比一比折出的三个图形，哪一个最大、哪一个最小呢？然后请学生通过操作验证自己的想法，从而得出分数大小的比较方法：平均分成的份数越多，每一份就越小。这节课上，学生在折纸的过程中，不仅仅完成了一系列的操作活动，更重要的是学生直观地理解了“分数”与“整体或单位1”之间的关系，以及如何比较几分之一的大小，分数知识的建立是在学生动手操作的基础上进行的。由于是人人动手折纸，人人动脑思考，使分数的含义建立得十分清晰和准确。
　　2.理解概念的本质特征
　　数学概念涉及两个方面：一是概念的“质”，也就是概念的内涵，即概念的本质属性；二是概念的“量”，也就是概念的外延，即概念中所有对象的和。只有从这两个方面指导学生学习概念，学生才能真正掌握概念的本质特征。
　　如，我在教学《圆的认识》时，重点抓了以下三个方面：①通过画圆认识圆心和半径。我给学生准备的工具是图钉、细绳和一枝铅笔，让学生独立画圆。画好后，引导学生小结，要想把圆画得标准，得注意两点，一是先固定一点，二是得把线拉直。在学生画的基础上，我利用课件重现了学生画圆的过程，使之在学生头脑中形成清晰的表象。这时就告诉学生这固定的一点叫圆心，这条拉直的线叫圆的半径。②认识圆的本质特征。由于学生经历了画圆的过程，看得到从圆心到圆上任意一点的线段的长（通过画圆的那根细绳）都相等，这就对圆的本质特征有了清晰的认识。③用圆规画半径不等的圆。我让每个学生用圆规画半径分别是2厘米、2.5厘米、3厘米的圆。通过画这些大小不等的圆，进一步理解圆的本质特征：不管是大圆还是小圆，都有“到定点的距离等于定长”的本质。在整个过程中，由于是学生亲力亲为，因此，学生真正领会到了概念的内涵。
　　二、让学生在“做数学”中获得基本的思想方法
　　使学生获得适应未来社会生活和进一步发展所必需的基本数学思想方法是《数学课程标准》提出的总体目标之一。数学思想方法是数学知识的精髓，是有效进行数学思考、解决社会生活问题和其他学科中诸多问题的有力武器。在小学数学中蕴含的数学思想方法主要有：演绎、归纳、类比、分类、转化、符号化、数形结合等。由于数学思想方法的习得是一个比较漫长的过程，它是伴随着基础知识与基本技能进行学习的，它和基础知识、基本技能的学习融为一体。因此，引导学生在“做数学”的过程中，我首先根据教学内容确定主要渗透的思想方法是什么，然后引导学生在不经意间应用该思想方法进行观察、尝试、分析、推理等活动，使学生在解决问题的过程中，感受思想方法的重要。
　　如去年11月在杭州举行的“千课万人”活动，我上了《分一分》这一课。这是六年级的一节综合应用课，要解决的问题是：
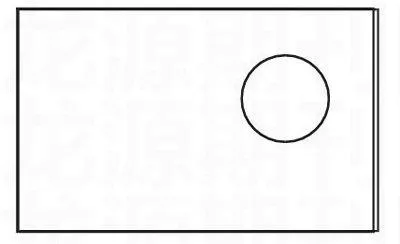
　　菜农张大伯家有一块长方形菜地，长100米，宽30米。菜地里有一口半径10米的圆形水池，张大伯要将这块菜地（水池除外）平均分成两份，分别交给他的两个儿子管理。你们能帮张大伯分一分吗？
　　在解决这个问题的过程中，我刻意进行了“转化与化归”思想方法的渗透。一是引导学生将实际问题转化为数学问题：“将菜地平均分成两份，就是寻找一条直线来等分右图，使两部分图形完全相同。”二是引导学生从已有的知识入手、从简单的问题入手，将复杂问题化为以下两个简单问题：①如果只有长方形（或只有圆），如何画一条直线将它分成两个完全相同的图形（过长方形的中心（或圆心）画一条直线）？②现在既有长方形又有圆（如上图），又如何画一条直线将它分成两个完全相同的图形呢？由于我为孩子们的思考心路铺设了拾级而上的台阶，提供了解决问题的思想方法，因此，多数学生很快找到了解决问题的结果：过长方形的中心和圆心，画一条直线，这条直线就是符合条件的直线了。
　　在这个过程中，学生获得的不仅仅是问题解决的最终结果，而是深深地体会到解决问题思想方法的重要，知道当遇到一个陌生问题时，应考虑如何将未知转化为已知，从陌生转化为熟悉，即如何学会用化归的方法来解决问题。这是数学教学的最终目的。
　　三、让学生在“做数学”中体验数学应用的价值
　　使学生“初步学会运用数学的思维方式去观察、分析现实社会，去解决日常生活中和其他学科中的问题，增强应用数学的意识”是《数学课程标准》提出的又一个目标。数学源于生活，生活中处处有数学。在教学中教师应经常让学生运用所学知识去解决现代生产、生活和其他学科学习中的实际问题，使学生在用数学的过程中一方面进一步巩固所学知识，另一方面深深感悟数学在社会生活中的地位和作用，体会数学的应用价值。
　　如，学习了一个因数是两位数的乘法和除数是两位数的除法后，我编拟了这样一个问题让学生解决。“据统计一个没有关紧的水龙头，每天大约滴18千克的水，这些水就这样白白流掉了。(1)照这样计算，一年(按365天计算)要浪费多少千克水？(2)把这些水分别装在饮水桶中(每桶约重15千克)，算算大约能装多少桶？(3)你家每月用几桶水？算算这些水够你家用几个月？大约合多少年？根据算出的这组数据，谈谈你的感想。”通过类似问题的解决，学生不但复习了所学的相关知识，而且发现了数据背后的大问题，体会到节约用水、爱护水资源的重要性。
　　总之，课堂教学中教师要充分调动学生的学习积极性，引导学生自主探索，把教学过程变成在教师指导下学生亲身经历、体验的参与学习过程，让学生充分体验参与、体验思维、体验创新、体验成功，让我们的学生在体验中自然和谐地发展。