基于理解性学习的教学设计——以“物质的量”（第一课时）为例

谢兆贵

（江苏省盐城中学 江苏 盐城 224005）

基于理解性学习的教学设计，把学生的理解视作重要的关注点。 “除非学生的知识是通过理解性学习而获得的，否则这些知识很可能一出校门就毫无用处。［1］”只有被学生理解了的知识，才能真正成为支撑学生今后发展的资源。 认知心理学的研究结果表明，建构有意义的联系是理解的心理实质， 是迁移和应用的心理基础；而就理解的过程而言，一定是学习者主动建构自己的知识经验的过程， 即通过新经验与原有知识经验反复的、双向的作用，不断地充实、丰富和改造知识经验。 但学习者建构对知识的理解并非是一种完全自发的心理机制，积极、自主、有意识的思维参与尤为重要，教学正是对这种建构过程的促进。

“物质的量”因其重要的认知价值和工具价值，一直是中学化学教学的重点；又因其本身的抽象性与学生认知水平欠缺间的矛盾，成为中学化学教学的难点。 而现行化学教材在编写上并未能弥补学生思维和认知上的不足［2］，也未能给教师的教学设计以恰当的引导，造成许多学生在学习该概念时，仍以机械接受为主，为整个高中阶段计算问题的解决埋下了隐患。 为了促进学生对“物质的量”概念的理解，进行了如下的教学设计。

一、设计先行组织者，联系学生的原有知识

意义学习是通过新信息与学生认知结构中已有的有关概念的相互作用才得以发生的。 “先行组织者”是先于学习任务本身呈现的一种引导性材料，能清晰地与认知结构中原有的观念和新的学习任务相联，为新的学习任务提供观念上的固定点。 为此，我们设计了如下的导入语作为“先行组织者”。

［师］同学们，我们已经知道，从宏观和微观两个角度认识物质是化学学科的重要特征，从定性和定量两个方面研究物质是化学学科的重要方法。 比如，对于我手上的这杯水而言，我们是如何认识它和研究它的？

上述导入语不仅为 “物质的量” 概念引入的意义——从微粒角度定量研究物质及其变化埋下了伏笔，而且以“水”及其变化“通电的条件下可生成氢气和氧气”为载体，通过师生的问答，理出如下可作为“物质的量”固定点的相关知识：①物质是由分子、原子、离子等微粒构成的；②物质化学变化的实质是微粒间的相互作用；③化学方程式中各物质的化学计量数之比实质上是它们的微粒个数比。 并在黑板上板书：

二、设计问题情境，激发学生有意义学习的心向

承接上述板书，教师设计以下的引语和问题情境：

［师］ 正是由于化学反应实质上是各物质以一定的微粒个数比进行的，所以，化学家们不仅要知道化学反应中的物质的质量，还需知道一定质量的物质中的微粒个数。比如，36g 水中究竟含有多少个水分子？36g 的水分解会生成多少个氢分子和氧分子呢？ 在日常生活中，我们常常通过数的方式来计量个数，那么对于分子的个数我们能否也通过数的方法获知呢？

［情境］ 一滴水中大约含有1.7 万亿亿个水分子，假设你一个一个地去数，每秒钟数240 个的话，请你计算大约需要多少年才能数完？

当学生运用已有经验不能解释新情境时，便引发认知冲突。 认知冲突在概念转变过程中具有关键意义，因为只有体验到认知冲突，个体才能感受到原有概念的不足，认识到替换或调整原有概念的必要性，激起有意义学习的心向。 上述问题情境的设计不仅让学生体会到分子之小以及数目之巨大，而且也让学生在“需要知道分子的数目”与“不能以个数去计量分子的数目”间产生冲突，激起探索“采用什么样的方法去计量微观粒子数目”的心向。

三、设计类比活动，联系学生的日常经验

学生难以理解“物质的量”概念的重要原因之一是概念本身抽象、远离学生的生活经验。 但其单位“摩尔”是具有集合思想的概念，是化学家基于研究和认识物质的需要而提出的。 这与日常生活中有时为了计数的需要运用“集合单位”的思想一致。 于是设计如下的活动：

［活动］ 张爷爷已收藏了65 年的硬币， 总共有40桶。 他决定将这些硬币存到银行，可是，他的财富对于银行工作人员来说，却意味着繁重的清点工作。 假如你是银行职员，你打算怎样清点这一笔数目巨大的硬币呢？［3］

这一活动的设计基于学生的日常经验，让学生在活动中理解，正如银行职员不会一个个地去数硬币数量一样，化学家也不会一个个地去数微粒数目，因为物质的微粒是如此之小而数量又如此巨大。并展示表1，以让学生实现从日常经验到科学认知的迁移。

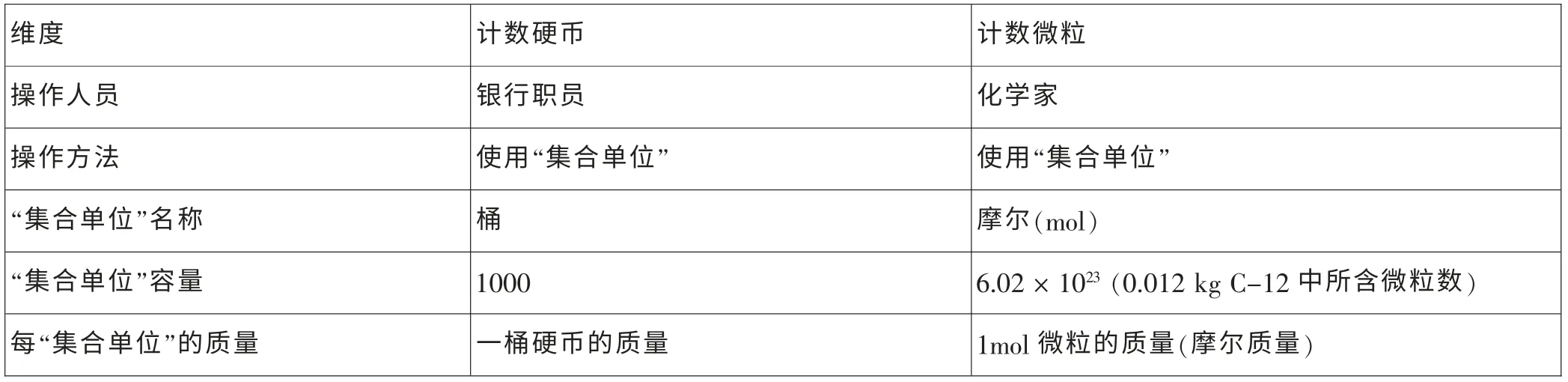
表1 银行职员和化学家的计数方法类比

四、揭示概念含义，联系学生已有认知结构

通过前面一系列教学活动的铺垫，学生已经明白了“为什么要计数微粒个数”、“如何计数微粒个数”， 此时再来揭示“物质的量”以及阿佛加德罗常数的概念就显得水到渠成， 且教师适时地将之与其它基本物理量比较，纳入学生已有认知结构中，如图1 所示。

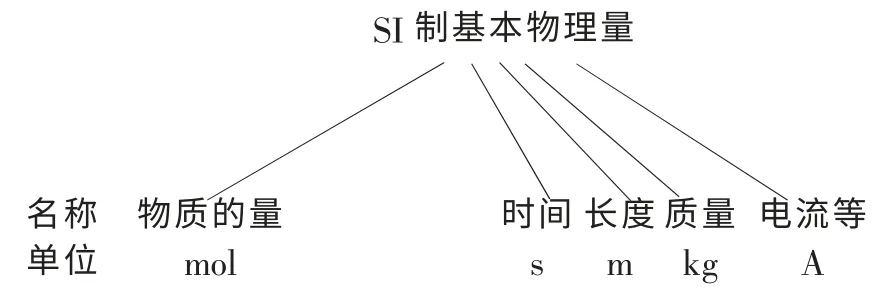
图1 基本物理量及其单位

该设计在概念呈现顺序上与教材有较大不同，教材中先有“物质的量”再引出“摩尔”。 但在教学实践中我们发现学生对“采用物质的量将一定数目的原子、离子或分子等微观粒子与可称量物质联系起来”这样的描述极为费解。 认知心理学认为，学习者对概念的心理认同感影响学生对概念的理解。 通过银行职员和化学家计数方法的类比学生已认同了摩尔这个概念， 再告诉学生“mol”是化学家为物理量“Amount of substance”所设计的单位，我们称之为“物质的量”。 并通过与其他并列概念的比较，学生就不难理解物质的量与时间、长度等一样都属基本物理量，只不过描述对象不一样而已。

五、设计推理活动，引导概念的纵深联系

前面的教学设计已让学生在新旧知识的相互作用中、与日常经验的联系中初步建立起物质的量及其单位摩尔概念的意义。 但对于为什么选取“0.012 kg C－12 中所含的碳原子数（阿伏加德罗常数）”而不用其它数作为1mol 的标准一定心存疑惑。 教师可顺势将此问题挑明：

［问题］为什么选取“0.012kg C－12 中所含的碳原子数（阿伏加德罗常数）”而不用其它的数作为1mol 的标准呢？

［引导性问题1］在以前的学习中，什么地方还用过C－12 作为标准？

［引导性问题2］那么这是巧合，还是化学家有意为之？

［活动］计算1mol 铝原子的质量

mc——1 个碳原子的质量；mAl——1 个铝原子的质量；Ar（Al）——铝原子的相对原子质量；NA——阿伏加德罗常数

推理：

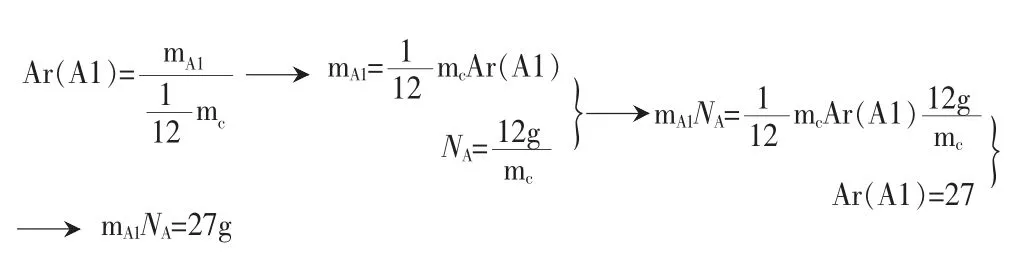
结论：1mol 铝原子的质量为27g， 在数值上等于Al的相对原子质量。

教材中只是通过简单呈现1mol 不同物质的质量从而引出摩尔质量。 当学生不知知识从何产生时，只能用“记住”去代替“理解”。 上述推导过程，不仅解除了学生对摩尔基准规定的疑惑，还让学生的逻辑思维有效参与到学习过程中来，对摩尔及摩尔质量的意义产生较为深刻的理解。

理解了摩尔质量的概念，前面所提出的36g 水中含有多少水分子的问题即可迎刃而解。 但对于36g 水分解能生成多少个氢分子和多少个氧分子，学生的思维还需经历化学方程式中的计量数之比即物质的量之比的跨跃。 于是设计以下的推理过程：

这一环节不仅是对前面问题的回应，也让学生深刻理解物质的量为何可用于根据化学方程式的计算，明白物质的量概念引入的意义所在。

六、设计整合环节，构建相互联系的结构化知识

要对知识形成深刻、真正的理解，学生所获得的知识就应是结构化的、整合的。 这种结构既能反映知识（概念或原理）之间的区别，又能反映知识之间的联系，以达到对概念的实质性理解；同时，这种结构又是开放的，随着后续的学习，将不断丰富和改造。

［师生共建结构图］

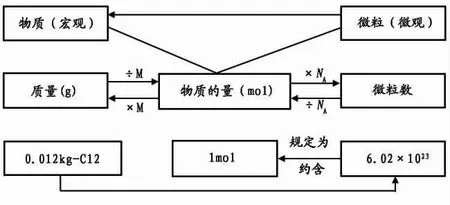
在日常教学中，我们常听到教师询问学生“你们听懂了吗？ ”“理解了吗？ ”但却不知如何做才能让学生理解。 上述教学设计以富于联系的理解性学习为设计的指导思想，概念形成和发展的线索清晰，且与学生的已有知识经验不断相互作用，运用问题情境不断调动学生思维的积极参与，让学生在问题解决过程中自主建构对知识的理解。 惟学生真正理解了概念，才能扫清后续学习及应用的障碍。

［1］ Thomas P.Carpenter，Richard Lehrer，Teaching and Learning Mathematics With Understanding，in：Mathematics Classrooms that Promote Understanding ［M］.Elizabeth Fenncma，Thomas A.Romberg，ed LEAPublisher，1999

［2］ 闫蒙钢，陈英.高中化学新教材（必修1）中“物质的量”内容的难度分析［J］.化学教育，2008，（5）：15－17

［3］ 改 编 自The McGraw－Hill Companies.Chemistry：Concepts and Applications ［M］. America： Columbus： Glencoe／McGraw－Hill， 2005