振动形成的单一尺寸硬球晶的结构表征及其动力学的离散元模拟
安希忠,李长兴,杨润宇,余艾冰,曲德毅
(1.东北大学 材料与冶金学院,沈阳 110004;2.新南威尔士大学 材料科学与工程学院颗粒系统模拟中心,澳大利亚 悉尼新南威尔士 2052;3.沈阳鼓风机集团股份有限公司,沈阳 110869)
振动形成的单一尺寸硬球晶的结构表征及其动力学的离散元模拟
安希忠1,李长兴1,杨润宇2,余艾冰2,曲德毅3
(1.东北大学 材料与冶金学院,沈阳 110004;2.新南威尔士大学 材料科学与工程学院颗粒系统模拟中心,澳大利亚 悉尼新南威尔士 2052;3.沈阳鼓风机集团股份有限公司,沈阳 110869)
采用离散元(DEM)数值方法结合物理实验,分别实现了单一尺寸硬球在三维(3D)间歇振动及批量加料条件下堆积的有序化(结晶),通过对晶体的结构表征、数值仿真中的微观性能如配位数(CN)、径向分布函数(RDF)、角分布函数(ADF)、Voronoi/Delaunay孔的尺寸分布、力的网络分析以及晶体形成过程中的动力学分析,得出如下结论:(1)数值仿真和物理实验中所获得的均为{111}取向FCC晶体,晶体中粒子的最大堆积密度可达0.74;(2)晶体中粒子的配位数分布在CN=12处出现峰值,表明每个粒子具有12个近邻;RDF和ADF分布表明堆积粒子之间分别在径向具有长程相关性及角度上具有相关性,这是晶态结构的典型特征;Voronoi/Delaunay孔的尺寸分布与非晶态相比表现为高且窄的曲线,且向左移,表明所获得的硬球晶中孔隙很小且分布均匀;粒子间力的网络更直观地表明了晶体的结构,同时还指出在FCC硬球晶中分别存在着面内的力和面间的力,其中后者小于前者;(3)晶体形成过程中的速度场和力场等动力学信息的变化表明粒子在堆积过程中一旦形成有序,它将作为一个整体运动,并为后续粒子的有序化提供模板,起到了结晶的晶核的作用.
颗粒堆积;致密化;振动;离散元模拟;硬球晶
无论是在工业生产还是在科学研究中,对硬球堆积致密化的研究一直是一个重要的课题[1,2].因为对于许多物理学家和材料学家而言,硬球的堆积可用于研究多种系统结构(直接研究这些系统的结构是相当困难的)的有效出发点.在过 去 的 几 十 年 里,从 Bernal[3],Scott[4]和Finney[5]等人首次利用硬球的堆积模拟简单液体结构取得成功以来,许多科学工作者又成功实现了硬球堆积非晶态(随机堆积)的转变[6~13],即从初始的松装密度约0.60转变为非晶态结构中硬球的最大堆积密度约0.64,在这个过程中,外部施加的振动起到了至关重要的作用.采用振动及合理地控制工艺参数也可以实现粒子的晶态堆积结构.这一点无论是从物理实验上还是从数值计算中都得到证实[14~23].但由于数值及物理实验中的特殊性,如现有的物理实验中对硬球结晶的动力学分析的难度,大多数数值仿真都是基于几何的模拟而忽略了动力学的范畴[21],从而导致所获得的结果很难再现实际的过程,故此对于完美硬球晶的形成过程及其动力学还有待于进一步的研究.
使用基于分子动力学的离散元(DEM)数值仿真,可以克服其他数值仿真方法的不足,从而从动力学的角度真实再现粒子堆积的致密化,DEM方法的有效性已经在许多科学研究中得到了证实[12,21,23~25].在以前的工作中[21],使用 DEM 模拟,我们已经成功实现了振动条件下完美硬球晶的获得.本文将在此基础上,对该硬球晶的宏观和微观性能及其形成过程的动力学进行分析,以期找出硬球振动堆积过程中有序化的规律,为实际完美硬球晶的获得提供参照.
1 模拟方法及条件
1.1 数值仿真方法
在DEM模拟中,每个粒子有两种运动形式,即平动和转动.根据牛顿第二定律,平动和转动方程可分别表示为

其中 mi,vi,ωi和 Ii分别表示粒子 i的质量、平动速度、角速度及转动惯量.Ri是由粒子i的中心指向接触点的矢量,其大小等于粒子i的半径Ri.法向接触力和切向接触力分别表示为

1.2 模拟条件
模拟由在一个长方体容器中随机产生一批无重叠的等同球形粒子开始,容器底面为边长为12 d(d表示粒子直径,模拟中所用的颗粒子直径d=1 cm)的正方形,为了避免容器壁的影响,在水平方向上采用了周期性的边界条件.初始时,随机产生的粒子在重力作用下自由下落,向下运动的过程中粒子与其近邻之间互相碰撞并来回弹跳跃.该动力学过程一直持续到所有粒子都达到稳定状态,此时由于能量完全耗散的结果,所有粒子的运动速度为零,这一过程在一秒钟内完成.一秒钟后,容器在相互垂直的3个方向上进行三维(3D)周期性正弦振动,每个方向上振动的控制方程为:Z(t)=Asin[ω(t-t0)],其中 Z 表示容器的位移,A和ω分别表示振动的振幅和频率.t0表示振动开始时间(本工作中t0=1.0 s),如果是1D振动,则只在竖直方向上施加周期性正弦振动.从位移方程很容易推导出振动的加速度方程:a(t)= -Aω2sin[ω(t-t0)].本研究中采用的是间歇振动、批量加料,即从1 s开始,粒子先振动1 s,此过程中以一定的批量加料,然后停止1 s使粒子达到稳定状态,接着再振动1 s,此时再加入下一批料,之后再停止1 s,……,这样的过程一直持续到振动结束.实验中所用的粒子为玻璃球,为了简化起见,取3D振动中3个方向上的振幅和频率分别相同.表1中列出了模拟中所用的参数及其所对应的取值,其中假定粒子与容器具有相同的性能.

表1 模拟中所用的参数Table 1 The parameters used in the simulation
2 研究结果及分析
2.1 硬球晶的实现
图1给出了硬球在3D间歇振动、批量加料的条件下,结晶过程中所对应的宏观性能如堆积密度ρ随振动时间t的演变及最终所获得的局部完美硬球晶体结构.图中的内插图是对密度变化曲线的局部放大,其中振幅A=0.1 d,振动频率ω=200 rad/s,每次加料的批量为Nb=98个粒子/批[21].可以看出在ρ-t曲线上存在着两个区域,第一个区域一直持续到28.0 s,在这期间堆积密度随时间增加.其中曲线上的起伏表示振动过程中对粒子堆积周期性压缩与松驰的结果.在第二个区域,振动使堆积密度沿着一个相对稳定的值变化.当振动停止时,球逐渐停下来形成稳定堆积,最终的堆积密度可达约0.74,结构表征发现其对应的是{111}取向的FCC晶体.图1中的DEM数值仿真结果由图2(其中的内插图为去除表面堆积粒子后所得到的内部有序结构)中的物理实验结果所验证[22].图2中的结果是在5个不同尺寸容器中展开的单一尺寸玻璃球在3D间歇振动(振幅A=0.4 d,振动频率ω=55 rad/s)及批量加料(Nb=1层/批)条件下得到的,为了消除容器壁的影响,我们对每种情况下不同容器中的实验结果进行了外推,结果得到在无限大容器中粒子的最大堆积密度可达约0.74,且对最终的堆积结构表征发现为{111}取向的FCC晶体,即在竖直的{111}方向上六方密排面的堆垛顺序为ABCABC……,体现了数值仿真结果和物理实验结果很好的一致性.

图1 3D间歇振动、批量加料时,晶态结构(内插图为原图的局部放大)的实现(左)及最终所对应的部分晶体(右),振动条件为:A=0.1 d,ω=200 rad/s,加料批量Nb=98粒子/批,图中A1为每一个振动周期内的振动开始点(在此处开始加料),A2为振动结束点[21]Fig.1 The realization of crystalline structure(left,the inset figure is the partial enlargement)and part of the final crystal(right)obtained under 3D interval vibration and batch-wised feeding,where the vibration condition is:A=0.1 d,ω =200 rad/s,batch of feeding Nb=98 particles/batch;A1represents the vibration starting point in each vibration period where the particles are fed at this moment,and A2is the end of vibration[21]
2.2 硬球晶的微观结构表征

图2 物理实验中,3D间歇振动、批量加料且A=0.4 d,ω=55 rad/s,Nb=1层/批时容器尺寸D(容器直径)对堆积密度的影响,内插图为去除表面粒子而得到的有序结构[22]Fig.2 The effects of container size on the packing density in physical experiments with 3D interval vibration and batch-wised feeding when A=0.4 d,ω =55 rad/s,and Nb=1 layer/batch,where the inset figures are the ordered structure obtained when the particles on the packing surface are removed[22]

图3 晶态结构的配位数分布Fig.3 Coordination number distribution of the crystalline structure
除了硬球晶宏观性能的演变外,我们也对所获得的硬球晶的微观性能进行了表征,这些微观性能包括:配位数(CN)、径向分布函数(RDF)、角分布函数(ADF)、Voronoi/Delaunay孔的尺寸分布以及晶体内力的网络结构,它们都是形成稳态的硬球晶后得到的.图3给出了硬球晶的配位数的分布,CN被定义为与给定粒子“接触”的粒子数,本工作中取临界距离为1.005 d,即如果两个粒子之间的距离小于该值,就被认为是接触.与非晶态结构CN分布的峰值为7不同地是[5,12,23,24],图3 中的 CN 分布的峰值对应于12,这是FCC晶体对应的配位数,表明我们所获得的结构是有序的.
与配位数CN相比,径向分布函数RDF和角分布函数ADF是表征晶体结构的更直接的方式.RDF定义为堆积中与特定粒子中心给定距离范围内发现一个粒子中心的概率,它包含了堆积粒子间径向相关性的有用信息;相对地,ADF定义为堆积中与特定粒子中心给定角度范围内发现一个粒子中心的概率,它包含了堆积粒子间角度相关性的有用信息.图4给出了我们所获得的最终硬球晶的RDF和ADF分布,与非晶态(随机密排)RDF 分布上的分叉第二峰不同[5,12,23,24],晶态结构的RDF分布还在r>2d的许多相关位置上出现了各种孤立的峰,这些在较远位置上的峰的存在表明了堆积体内粒子之间位置的长程相关性,这是晶态结构的典型特征[21].同样,我们所获得的晶态结构的ADF也与非晶态结构的ADF分布完全不同,后者在图上表现在角度在60(°)~180(°)之间的一条连续的曲线,而前者的ADF只在60(°)、90(°)、120(°)和180(°)的角度上存在明显的峰,这表明堆积体内粒子之间存在着角度的相关性,这进一步表明了我们所获得的硬球堆积结构为晶态而不是非晶态[23].
对所获得硬球晶局部结构更具体的分析来自于 Voronoi和 Delaunay 对空间的划分[29~33],它比图4中的一维RDF和ADF能够提供更丰富的信息[34].Voronoi空间划分是通过 Voronoi多面体来实现的,它定义为堆积体内垂直平分给定粒子中心与其他粒子中心之间线段的面所围成的最小封闭凸多面体[30],如果连接堆积体内每个粒子与其近邻粒子中心,则会构成一个空间网络,该网络则称为Delaunay的空间划分.网络中的四面体单体形成了对空间的完全填充.图5中给出了Voronoi(内插图为Delaunay)的孔的尺寸分布,我们将Voronoi或Delaunay单体内孔的体积V除以粒子的体积Vp而使其无量纲化.由图可见,无论是Voronoi还是Delaunay孔的尺寸分布,都呈现出高且窄的趋势,并且明显小于粒子的体积.这表明晶态结构中孔的尺寸很小且分布很均匀;这一点与非晶态结构中呈现右移的宽且矮的Voronoi/Delaunay孔的尺寸分布完全不同[12].
为了更直观的表征硬球晶的内部结构,我们也给出了最终部分硬球晶的力的网络结构,如图6所示.图中的“球”表示晶体中堆积的粒子,“棍”表示粒子之间的力,“棍”的粗细与力的大小成正比.从图中除了可以很清晰地看出所形成的是{111}取向FCC晶体以外,更重要地是我们可以得到力在晶体中传播的信息,即在晶体中存在着面内的力和面间的力.在堆积中的每个球都可以看作是一个“外部载荷”,在这些“外部载荷”的作用下,力可以沿着三角架的方向传递,从而形成面间的网络,这与Mueggenburg等人[35]的实验结果相一致,所不同的是,在我们的结果有存在着较大的面内的力.
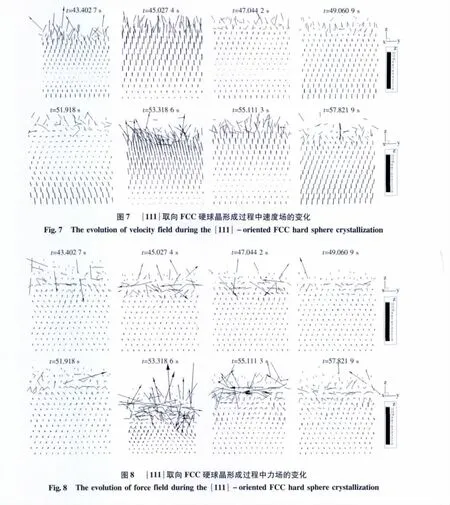
2.3 硬球晶形成的动力学分析
除了前面对最终硬球晶的宏观性能和微观性能进行表征外,我们还从动力学的角度研究了硬球晶的形成过程.硬球结晶过程中的速度场和力场的变化分别如图7和8所示.这两个图中显示地是三维矢量场中的二维视场,其中视角的方向为沿着X轴的方向.从这两个图中我们可以发现堆积过程中出现的几个特征.首先,是振动过程所带来的对粒子的激发及松驰过程,其中对粒子的激发发生在t=53.318 6s,在这个过程中粒子的运动速度和力都很大.而粒子的松驰发生在t=47.044 2 s,此时粒子的速度和力逐渐减弱,渐渐形成稳定结构.不管是激发还是松驰,粒子运动最剧烈地是在表面,这可以从速度和力的变化反映出来,这是因为表面粒子在振动堆积致密化过程中由于缺少约束而处于流化状态,随着外部输入能量的停止,它们将找到各自的稳定位置从而形成有序的结构.另一方面,在有序堆积过程中,先堆积的粒子的运动状态基本相同,也就是说在底层形成有序结构后,其中粒子的速度和力的变化不大,因此,在振动过程中其是作为一个整体运动的,它作为后续粒子有序化堆积的模板,起到了结晶的晶核的作用,这一点已经在我们的数值仿真[23]和物理实验[22]中得到了证实.

图4 晶态结构的径向分布函数(左)和角分布函数(右)Fig.4 Radial distribution function(left)and angular distribution function(Right)for the crystalline structure
3 结论
采用离散元(DEM)数值方法模拟了单一尺寸球形粒子在三维(3D)间歇振动及批量加料条件下堆积的有序化(结晶),并对所获得的硬球晶的宏观性能如堆积密度及微观性能如配位数CN、径向分布函数 RDF、角分布函数 ADF、Voronoi/Delaunay孔的尺寸分布及力的网络结构进行了表征,同时从动力学角度分析了硬球堆积有序化过程中的速度场和力场的变化,得出结论如下:
(1)对单一尺寸粒子在3D间歇振动及批量加料条件下堆积的DEM模拟可以获得最大堆积密度达0.74的硬球晶,同时,该过程已得到了物理实验的验证.
(2)硬球晶的配位数(CN)分布在CN=12处出现峰值,结构表征发现对应的为FCC晶体;径向分布函数(RDF)和角分布函数(ADF)的表征发现晶体中的粒子分别存在径向的长程相关性及角度的相关性,这是晶态结构区别于非晶态结构的典型特征;Voronoi/Delaunay孔的尺寸分布表现为左移的高且窄的峰,表明堆积结构中的孔的尺寸很小且分布均匀;力的网络直观的表现了晶体的结构,同时表明所形成的{111}取向FCC硬球晶中,在面内和面间均有力的存在,且面内的力大于面间的力.
(3)通过对粒子振动堆积有序化过程中的动力学信息如速度场和力场变化的分析,发现硬球在结晶的过程中,一旦有序结构形成,该有序结构中的粒子在后面的振动过程中保持相同的运动状态,即作为一个整体运动,它为后面有序化的继续提供了模板,起到了晶核的作用.
[1]German R M. Particle packing characteristics[M].Princeton,New Jersey:Metal Powder Industries,1989:1-18.
[2]Bideau D,Hansen A.Disorder and granular media,random materials and process[M].Edited by Stanley H E,Guyon E,North - Holland.Amsterdam:Elsevier Science Publishers,1993:1-25.
[3]Bernal J D.A geometrical approach to structure of liquids[J].Nature,1959,183(4655):141-147.
[4]Scott G D.Packing of spheres[J].Nature,1960,188(4754):908-909.
[5]Finney J L.Random packings and the structure of simple liquids:I the geometry of random close packing [J].Proc Roy Soc Lond A,1970,319:479-493.
[6]Woodcock L V.Glass transition in the hard-sphere mode[J].J Chem Soc Faraday II,1976,72:1667-1672.
[7]Finney J L.Modelling the structures of amorphous metals and alloys[J].Nature,1977,266:309 -314.
[8]Zallen R.The physics of amorphous solids[M].New York:Wiley,1983:1-15.
[9]Knight J B,Fandrich C G,Lau C N,et al.Density relaxation in a vibrated granular material[J].Phys Rev E,1995,51(5):3957-3963.
[10]Torquato S.Glass transition:hard knock for thermodynamics[J].Nature,2000,405:521 -523.
[11]Stachurski Z H.Definition and properties of ideal amorphous solids[J].Phys Rev Lett,2003,90(15):155502.
[12]An X Z,Yang R Y,Dong K J,et al.Micromechanical simulation and analysis of one-dimensional vibratory sphere packing[J].Phys Rev Lett,2005,95:205502 -1 -4.
[13]An X Z,Li C X,Yang R Y,et al.Experimental study of the packing of mono-sized spheres subjected to one-dimensional vibration[J].Powder Technol,2009,196:50 -55.
[14]Owe Berg T G,Mcdonald R L,Trainor R J.The packing of spheres[J].Powder Technol,1969/1970,3:183 -188.
[15]Pouliquen O,Nicolas M,Weidman P D.Crystallization of non-Brownian spheres under horizontal shaking[J].Phys Rev Lett,1997,79:3640 -3643.
[16]Van Blaaderen A,Ruel R,Wiltzius P.Template-directed colloidal crystallization[J].Nature,1997,385:321 -324.
[17]Blair D L,Mueggenburg N W,Marshall A H,et al.Force distributions in three-dimensional granular assemblies:effects of packing order and interparticle friction[J].Phys Rev E,2001,63:041304.
[18]Nahmad-Molinari Y,Ruiz-Suárez J C.Epitaxial growth of granular single crystals [J]. Phys Rev Lett, 2002,89:264302.
[19]Kansal A R,Torquato S,Stillinger F H.Diversity of order and densities in jammed hard - particle packings[J].Phys Rev E,2002,66:041109-1-8.
[20]Spannuth M J,Mueggenburg N W,Jaeger H M,et al.Stress transmission through three-dimensional granular crystals with stacking faults[J].Granular Matter,2004,6:215 -219.
[21]Yu A B,An X Z,Zou R P,et al.Self-assembly of particles for densest packing by mechanical vibration[J].Phys Rev Lett,2006,97:265501.
[22]Li C X,An X Z,Yang R Y,et al.Experimental study on the packing of uniform spheres under three-dimensional vibration[J].Powder Technol,2011,208(3):617 - 622.
[23]An X Z,Yang R Y,Dong K J,et al.DEM study of crystallization of monosized spheres under mechanical vibrations[J].Computer Physics Communications,2011,182:1989 -1994.
[24]Yang R Y,Zou R P,Yu A B.Computer simulation of the packing of fine particles[J].Phys Rev E,2000,62(3):3900-3908.
[25]An X Z,Yang R Y,Zou R P,et al.Effect of vibration condition and inter-particle frictions on the packing of uniform spheres[J].Powder Technol,2008,188(2):102-109.
[26]Martin C L, Bouvard D, Shima S. Studyofparticle rearrangement during powder compaction bythe discrete element method[J].J Mech Phys Solids,2003,51(4):667-693.
[27]Schwager T,Pöschel T.Coefficient of normal restitution of viscous particles and cooling rate of granular gases[J].Phys Rev E,1998,57(1):650-654.
[28]Langston P A,Tüzün U,Heyes D M.Discrete element simulation of granular flow in 2D and 3D hoppers:dependence of discharge rate and wall stress on particle interactions[J].Chem Eng Sci,1995,50(6):967 -987.
[29]Oger L,Gervois A,Troadec J P,et al.Voronoi tessellation of packing of spheres:topological correlation and statistics[J].Phil Mag B,1996,74:177-197.
[30]Yang R Y,Zou R P,Yu A B.Voronoi tessellation of the packing of fine uniform spheres[J].Phys Rev E,2002,65:041302.
[31]Aste T,Saadatfar M,Senden T J.Geometrical structure of disorderedspherepackings [J]. Phys Rev E,2005,71:061302.
[32]Yang R Y,Zou R P,Yu A B,et al.Pore structure of the packing of fine particles[J].J Colloid Interface Sci,2006,299:719-725.
[33]An X Z.Evolution of Voronoi/Delaunay characterized micro structure with transition from loose to dense sphere packing[J].Chin Phys Lett,2007,24(8):2327 -2330.
[34]Montoro J C G,Abascal J L F.The Voronoi polyhedra as tools for structure determination in simple disordered systems[J].J Phys Chem,1993,97:4211-4215.
[35]Mueggenburg N W,Jaeger H M,Nagel S R.Stress transmission through three-dimensional ordered granular arrays[J].Phys Rev E,2002,66:031304-1.
Structure characterization on the vibration induced mono-sized hard sphere crystal and its dynamics by DEM modeling
AN Xi-zhong1,LI Chang-xing1,YANG Run-yu2,YU Ai-bing2,QU De-yi3
(1.School of Materials and Metallurgy,Northeastern University,Shenyang 110004,China;2.Laboratory for Simulation and Modeling of Particulate System,School of Materials Science and Engineering,University of New South Wales,Sydney 2052,Australia;3.Shenyang Blower Works Group,Co.,Ltd.,Shenyang 110869,China)
In this paper,the ordering(Crystallization)of mono-sized sphere packing under three-dimensional(3D)interval vibration and batch-wised feeding was studied with numerical discrete element method(DEM)combined with the physical experiments.Through the characterization on the crystalline structure and the analysis on the micro-properties obtained numerically such as coordination number(CN),radial distribution function(RDF),angular distribution function(ADF),Voronoi/Delaunay void size distribution,force network and the dynamics formed during ordering,following conclusions can be drawn:(1)The crystalline obtained both numerically and physically all indicates{111} -oriented FCC structure,where the maximum packing density can reach 0.74;(2)There is a peak at CN=12 in the coordination number distribution curve,which implies that each particle in the hard sphere crystal has 12 neighbors in contact;the distributions for RDF and ADF show the long range correlation in radial distance and angle correlation among particles,which are the typical characteristics of the crystalline structure;the Voronoi/Delaunay void size distribution indicates the higher and narrower curve shifting to the left compared with non-crystal state,which means that the voids in crystalline structure are small and uniform;the force network among particles can identify the crystalline structure more intuitively,meanwhile,it’s also indicated that the in - plane forces and inter- plane forces coexist in the crystal,and the latter is smaller than the former;(3)The variation of dynamic information such as the velocity field and the force field all indicates that once the ordered structure formed during crystallization,it will move as a whole part,which served as the template for the other particles,i.e.as the nucleus inthe crystallization.
particle packing;densification;vibration;DEM simulation;hard sphere crystal
TF 122;TB 44;O 756
A
1671-6620(2011)04-0318-07
2011-09-20.
国家自然基金 (50974040),中央高校基本科研业务费 (N100402009),澳大利亚研究委员会基金 (DP0665276).
安希忠 (1973—),男,辽宁盖州人,东北大学副教授,E-mail:anxz@mail.neu.edu.cn

