K1,m□K1,n的均匀染色

黄大江,何文杰

(河北工业大学理学院应用数学研究所,天津 300130)

K1,m□K1,n的均匀染色

黄大江,何文杰

(河北工业大学理学院应用数学研究所,天津 300130)

一个图G可均匀k-染色,如果它的点集可分为k个独立集合,使得每两个不同集合中点的数目最多差1。使这种染色存在的最小数k称为图G的均匀染色数,记作x=(G)。在本文中,得到了关于图K1,m□K1,n的均匀染色结果,2≤x=(K1,m□K1,n)≤4。

星图;均匀染色;笛卡尔积

1 引言

令G=(V(G),E(G))是一个简单图,用V(G)和E(G)分别表示G的顶点集和边集。G中的一个元素是G的一个点或一条边。边{u,v}记作uv或vu。两个图G1=(V1,E1)和G2=(V2,E2)的笛卡尔积G1□G2是这样一个图,它的点集是V1×V2,点(a,b)与点(c,d)相邻接当且仅当a=c且b与d相邻接,或者b=d且a与c相邻接。一个图G被称作是均匀k-可染的,如果它的点集可分为k个类V1,V2,…, Vk,使得每一个V i都是独立集,且满足‖V i|-|V j‖≤1其中1≤i,j≤k。满足上述条件的最小的数k被称为图G的均匀染色数,记作x=(G)。

1973年,M eyer[5]提出了下面的猜想。

猜想1(均匀染色猜想)对于除了完全图和奇圈的任何一个连通图G,都有x=(G)≤Δ(G)。这里有关于一些图笛卡尔积的均匀染色结果:

定理1.1[2]如果G1和G2都是均匀k-可染的,那么G1□G2也是均匀k-可染的。

定理1.2[2]

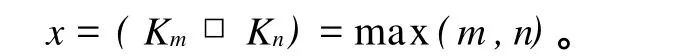
定理1.3[2]令G1(V1,V2,…,V r)和G2(V1′,V2′,…,V r′)是任意两个r-剖分图,使得|V1|′=|V2|′=…=|V r|′成立,那么有x=(G1□G2)≤r。

定理1.4[2]令k,m,n和r都是正整数。那么以下图的均匀染色数都等于2。G2m□G2n,Pm□Pn, Qr□G2n,Kk,m□G2n,K1,m□G2n,Pm□P2n,Qr□P2n,Kk,m□P2n,K1,m□P2n,QrQr,其中Pm是一条路长为|Pm|=m+1的路,Qd是一个超立方体,Kk,m是完全二分图。

定理1.5[1]令G1为具有n个点的图,G2是n-可染的。那么G1□G2是均匀n-可染的。

定理1.6[3]令G=G(X,Y)是一个连通二分图。如果G不同于任何一个完全二分图Kn,n,那么G可以被Δ(G)种颜色均匀染色。

定理1.7[4]假设pi是正整数且M是满足pi(modM)<「pi/M┒其中i=1,…,n的最大整数。那

2 K1,m□K1,n的均匀染色

现在令m,n都为正整数,不失一般性,可以假设m≤n,考虑星图G1=K1,m和G2=K1,n,我们用a0(b0)标记G1(G2)的中心点,用a1,a2,…,am(b1,b2,…,bn)标记G1(G2)的其他点,用a0b0,a0b1,…,a0bn, a1b0,a1b1,…,a1bn,…,am b0,…,am bn来标记K1,m□K1,n中的点.按照以下来排列这(m+1)(n+1)个点。

如果m=2k+1,n=2l+1,其中k,l均为正整数,那么把图K1,m□K1,n中的(m+1)(n+1)个点分成16个区域,其中每一个区域都是由相互独立的点组成的。

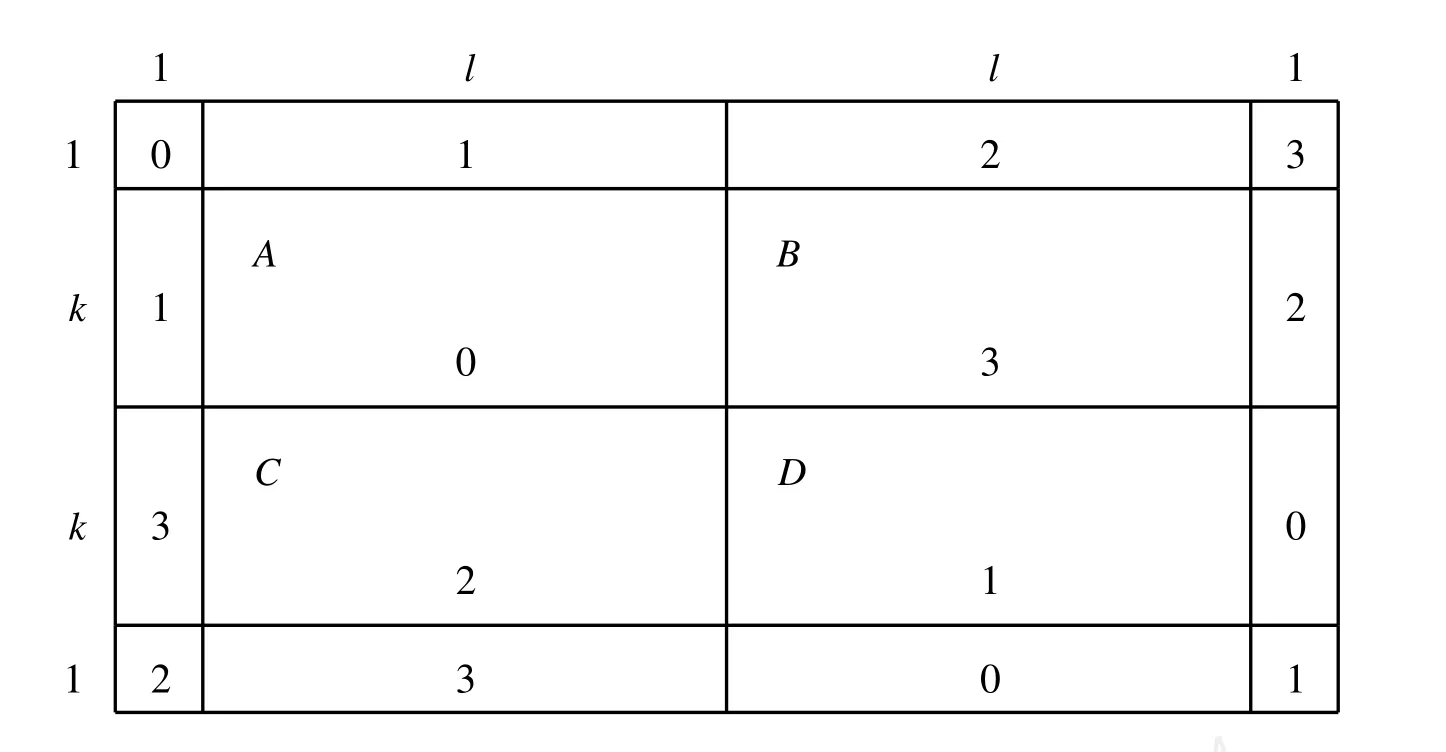
用0,1,2,3来染这些点并且把它们标记在相应的区域。易见这是一个正常染色,并且染了0,1,2,3的点的数目分别为:

那么,从区域D任选┖(k-1)/2」个点,把它们的颜色从1变为0;从区域B任选┖(k-1)/2」个点,把它们的颜色从3变为1;从区域A任选┖(k-1)/2」个点,把它们的颜色从0变为2;完成这些操作之后,染了同种颜色的点仍然都相互独立并且

接下来,从区域D任选┖(l+k)/2」个点,把它们的颜色从1变为0;从区域C任选┖(l-k)/2」个点,把它们的颜色从2变为0;从区域A任选┖(l-k)/2」个点,把它们的颜色从0变为3;完成这些操作之后,染了同种颜色的点仍然都相互独立并且

[1] Bor-Liang Chen,Ko-Wei Lih.Equitable Coloring of Interval Graphs and Products of Graphs,arX-iv:0903.1396v1[math. CO],2009.

[2] Hanna Furmańcyzk,EQU IT ABL E COLORING OF GRA PH PRODU CTS some,Opuscula M athe matica.Vol 26(2006)No.1.

[3] Peter Che Bo r Lam,Wai Chee Shiu,On the equitable chromatic number of com p lete n-partite graphs[J].Discrete App lied M athematics.2001,113:307-310.

[4] Ko-Wei Lih,Pou-Lin WuOn equitable coloring of bipartite graphs[J].Discrete Mathematics.1996,151:155-160.

[5] W.MeyerEquitable coloring,Amer.Math.Monthly.1973,80:920-922.

Equitable coloring of K1,m□K1,n

HUANGDa-jiang,HEWen-jie

(A pplied M athematics Institute,Hebei University of Technology,Tianjin300401,China)

A graph G is equitablyk-colorable if its vertices can be partitioned intokindependent sets in such a way that the number of vertices in any two sets differs by atmost one.The smallestkfor w hich such a colo ring exists is know n as the equitable chromatic num ber ofGand deno tedX=(G).In this paper,we obtain result on equitable coloring ofK1,m□K1,n.2≤x=(K1,m□K1,n)≤4.

Star graph;Equitable colo ring;Cartesian p roduct

O157

:A

1001-9383(2011)01-0001-05

2010-09-12

国家自然科学基金资助项目(10871058)

黄大江(1985-),男,河北邢台人,硕士研究生,从事图的染色问题的研究.