RSA算法硬件实现的几个关键技术
尹绪昆,黄世中
(河北省科学院应用数学研究所,河北石家庄 050081)
RSA算法硬件实现的几个关键技术
尹绪昆,黄世中
(河北省科学院应用数学研究所,河北石家庄 050081)
介绍了RSA算法硬件实现的关键技术的基本思想。通过这些技术,可以极大增加算法的运行效率。
RSA;中国剩余定理;Montgomery;进位保留加法器;超前进位加法器
RSA算法是当前世界首选的公钥加密算法。目前在美国和欧洲的商务和政务一直使用。著名密码学家Steve Burnett和Stephen Paine在《security official guide to cryp tography》指出:自1977年以来,尽管世界各国的研究人员发明了许多公钥算法,但排在第一位的是仍然是RSA,其次是DH,然后是ECC。
大数模幂乘运算是很多公钥密码体制例如RSA的核心运算,它由一系列的模乘运算组成,大数的位数往往多达1024 bit或更多,运算量极大,是提高加解密运算速度的瓶颈。开发一种高速、实时并且安全的RSA密码系统,仍然是一个挑战。采用超大规模集成电路来实现RSA算法的运算,这种实现方法比普通的PC机用软件进行1024位数字签名要快上百倍。
下面介绍一下RSA硬件实现的关键技术。
1 Montgomery模乘法算法
模乘幂运算是由一系列的模乘法运算完成。在实现大整数的模乘法运算的所有算法中,Montgomery模乘法算法不依赖于大整数的比较和除法,是一种便于硬件实现的算法。
1985年Montgomery提出了一种模乘的算法,其设计思想是借助一个新的特殊剩余系数,将普通模乘转化为易计算的模乘。Montgomery算法是基于以下结论:
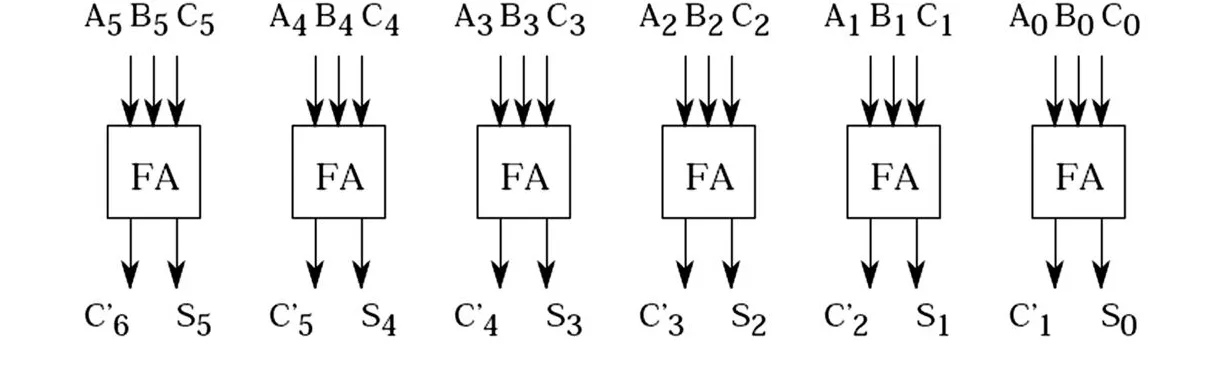
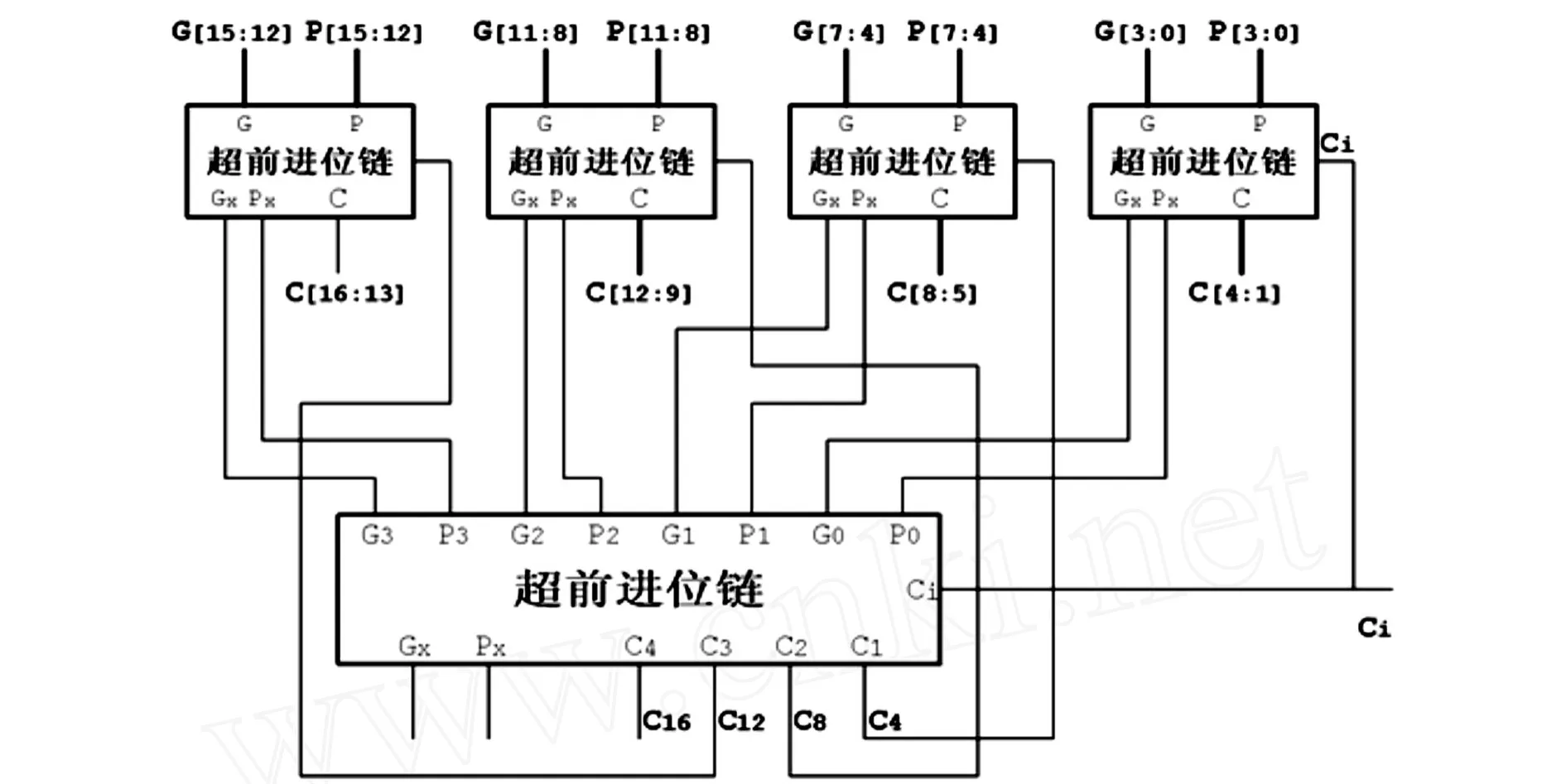
假设2n-1≤N≤2n,R=2n且N与R互素,A,B 这样算法中的整数模R约化和整数除以R运算只需要通过简单的截取或移位就能实现,从而避免了复杂耗时的除法运算。这就是Montgomery算法的根本精髓所在。 需要指出的是Montgomery模乘法算法对于单独的一次模乘运算并无什么优势,因为它要经历对剩余系数的映射、具体Montgomery乘积计算和反映射三个阶段。但对于模同一个数的连续的多个模乘运算,如模幂运算,具有很大的优势。 经过S.E.Eldrifge和C.D.Walter改进以后的Montgomery算法可以按如下的方法来实现: 基于2为基的Montgomery模乘算法 实际采用改进的基于2为基的Montgomery模乘法,即通过略微增加循环数量,减少中间步骤的复杂性(如可以去掉第7步的判断),从而利用流水线技术来提高整个系统的工作主频。 长的数据宽度,限制了许多原有的加法、乘法运算结构的使用,因为他们需要很大的面积;同时其引起的长进位链是个难以解决的问题,因为其极大地影响了系统主频的提高。因此可以采用进位保留加法器结构(CSA)实现,即输入输出采用普通表示,中间结果采用进位保留形式,最后采用一个32位的CLA(超前进位加法器)对乘法结果进行格式转换。这一方法即充分利用的硬件的并行性,减少了由于长进位链产生的逻辑延迟,提高了工作主频,也降低系统的面积。为了进一步利用CSA的并行性,还可以采用2个CSA的4:2结构或3个CSA的5:3结构。 进位保留加法器CSA结构如图1: 图1 进位保留加法器结构 CSA相当于k个并行的全加器(FA),输入3个k位整数A、B、C,产生2个整数C′和S,满足C′+S =A+B+C。CSA不存在长进位链的问题,利于实现硬件的并行处理。 超前进位加法器(CLA)克服了普通加法器不佳的时序特性,不单纯将前一级产生的进位信号以串接的方式传递到当前一级的全加器,而是利用了逻辑代入的方式来减少进位延迟时间。 可见,将迭代关系去掉,则各位彼此独立,进位传播不复存在。因此,总的延迟是两级门的延迟。其高速也就自不待言。 但是当加法器的位数增大时,如果仍采用上述的迭代公式,形成的电路将很不规则,并且需要长线驱动以及大驱动信号和大扇入门。可以对电路进行改进,用两个16位加法器来构成32位的加法器。 设Ci为开始输入的进位,对于16位CLA的超前进位链,考察第4、8、12、16位的进位,会得到: 于是对于16位加法器,按4位一组的形式对其分组,组内实行超前进位,组间也实行超前进位。结构如图2所示。第一级中每个4位的CLA模块分别计算各组内的G,P和组间的PX,GX,第二级根据各组的PX,GX计算出组间的进位。 图2 16位超前进位加法器原理图 由于RSA加密运算的公钥一般都取固定的小整数(如3或65537),而解密运算的私钥往往高达1024bit甚至更多,因此解密(签名)的速度明显低于加密(验证)的速度。为了进一步提高解密(签名)的速度,在自己知道生成RSA密钥的素数对的前提下,可采用中国剩余定理(CRT,Chinese Remainder Theorem)通过降低模乘幂运算的大整数的长度,达到提高运算速度的目的。 中国剩余定理(CRT)设m1,m2,…,mk是两两互素的正整数,则同余方程 1.取两个素数p和q(保密); 2.计算n=pq(公开),φ(n)=(p-1)(q-1)(保密); 3.随机选取整数e满足 (e,φ(n))=1(公开); 4.计算d,满足de≡1 modφ(n)(保密)。 综上所述,采用上述的关键算法,不管是用FPGA,还是用ASIC来实现,都可以明显提高算法芯片的运算速度。 [1] M c Ivor C,M cLoone M,McCanny J,et al.Fast Montgomery Modular M ultiplication and RSA Cryptographic Processor A rchitectures[C].Proceedings of the 37th Asilomar Conference on Signals,Systems,and Computers.New York:IEEE Press,2003. [2] Blum T,Paar C.Modular Exponentiation on Reconfigurable Hardware[C].Proceedingsof the 14th IEEE Symposium on Computer A rithmetic(ARITH-14).New York:IEEE Press,1999 Some key technologies of implementing RSA algorithm via hardware YIN Xu-kun,HUANG Shi-zhong (Institute of A pplied M athematics,Hebei Academ y of Sciences,Shijiazhuang Hebei,050081,China) In this paper,the basic thoughts of imp lementing RSA algorithm via hardware are introduced.These methods can increase run efficiency of the user’s p roducts greatly. RSA;Chinese Remainder Theorem;Montgomery;CSA;CLA TP319 :A 1001-9383(2011)01-0010-05 2010-11-20 尹绪昆(1979-),男,河北武安人,助理工程师,主要从事计算机技术应用与开发.

2 进位保留加法器结构CSA
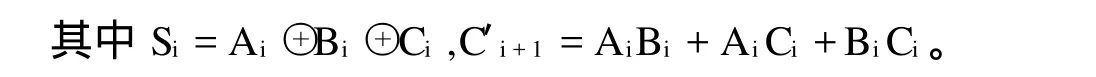
3 超前进位加法器CLA


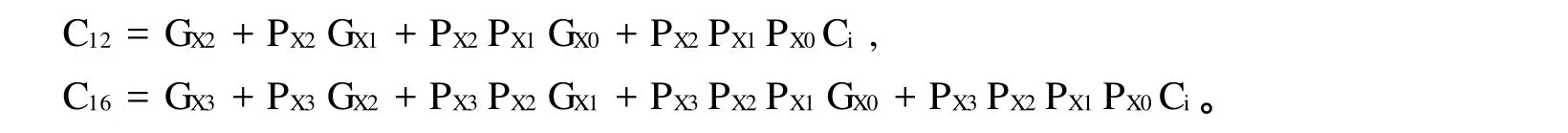
4 中国剩余定理
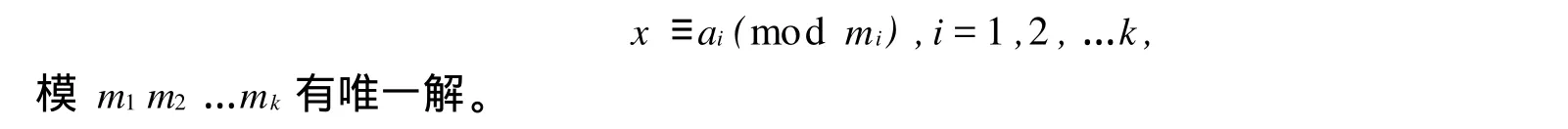
4.1 RSA加密算法的过程是
4.2 RSA密钥结构


4.3 RSA加密程序

4.4 RSA解密程序

4.5 RSA解密程序(带CRT)(速度提高4倍)

5 结束语

