二阶矩随机Hilbert边值问题

姚村，林峰

（华侨大学 数学科学学院，福建 泉州 362021）

二阶矩随机Hilbert边值问题

姚村，林峰

（华侨大学 数学科学学院，福建 泉州 362021）

通过对称扩张的方法，把二阶矩随机Hilbert边值问题转化为二阶矩随机Riemann边值问题，最终求解二阶矩随机Hilbert边值问题.

边值问题；Hilbert问题；Riemann问题；二阶矩；对称扩张；随机过程

设L是一简单光滑闭曲线，以反时针方向为正，它把复平面C分成内部区域S＋和外部区域S－，（Ω，F，P）是概率空间.文献［1］讨论了随机奇异积分的存在性，并且得到了随机Cauchy型积分的Plemelj公式；文献［2］讨论了随机Riemann边值问题的解.本文通过对称扩张的方法［3］，求解随机Hilbert边值问题.

1 预备知识

随机 Hilbert边值问题是指，求在S＋内均方解析的复随机过程Φ＋（ω，z）＝u（ω，z）＋i v（ω，z），均方连续到S＋＋L上，满足边值条件）

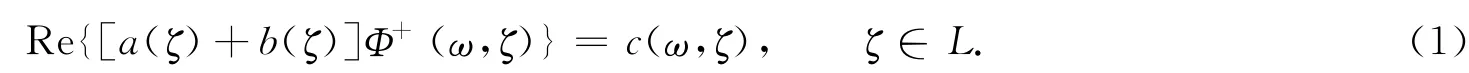
式（1）中：a（ζ），b（ζ）都是已给在L上∈H 的实函数；c（ω，ζ）是（Ω，F，P）上的一个实值随机过程，它依赖于参数ζ∈L，假定它是一个二阶矩过程，并且满足

式（1）也可改写为

由于经过保形映射，可以把S＋变为单位圆内部，而L变为其圆周，且仍以反时针方向为正向.这样，只考虑问题（1）在L为单位圆时的解，以下总假设S＋就是单位圆域｜z｜＜1，L是单位圆周｜ζ｜＝1.

2 随机函数在圆外的扩张

为了求解圆内随机Hilbert问题，应设法把它转化为随机Riemann问题 .把单位圆域S＋中的随机函数Φ（ω，z）按如下定义给出其在外域S－中的对称扩张或对称函数，有

定理1 若Φ（ω，z）在S＋内均方解析，则Φ＊（ω，z）在S－内均方解析.

证明 因Φ（ω，z）在S＋内均方解析，则存在随机过程η（ω，z），使得

由 Loeve准则［4］可知

又有

由 Loeve准则［4］可知

即知Φ＊（ω，z）在S－内均方解析.

如果Φ（ω，z）能从S＋内均方连续延拓到单位圆周L∶｜ζ｜＝1上，则Φ＊（ω，z）也能从S－内均方连续延拓到L上，且因为，故有

从而，若Φ（ω，z）在S＋内均方解析，均方连续于S＋＋L上，则有

这就是一分区均方解析函数，以L为跳跃曲线，它在L上的边值满足条件为

3 随机Hilbert边值问题的转化

假定a2＋b2≠0在L上.利用上段方法，把所求函数Φ＋（ω，z）＝Φ（ω，z）对称扩张到S－中，可得分区均方解析函数Ω（ω，z）（式（5）），则可把式（1）改写为（a（ζ）＋i b（ζ））Ω＋（ω，ζ）＋ （a （ζ）－i b（ζ））Ω－（ω，ζ）＝2c（ω，ζ）， ζ∈L. （7）

又因为a（ζ），b（ζ）∈H，因此可得

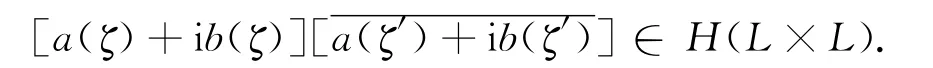
再由Rc（ζ，ζ′）∈H（L×L），可知

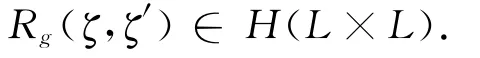
由此，问题（1）可转化为随机Riemann问题，即

满足条件式（6）的随机Riemann问题（8）的解，就是问题（1）的解.所以只需求出随机Riemann问题（8）的解Ω（ω，z），作出Ω＊（ω，z），再求出

便是原问题（1）的解Φ（ω，z）＝Ω0（ω，z），z∈S＋.

4 随机Hilbert边值问题的求解

设X（z）为G（ζ）的典则函数，问题（8）的指数为κ＝IndLG（ζ），是一偶数.

下面，对随机Hilbert边值问题进行求解.

（i）当κ≥0时，由文献［2］可知，随机Riemann问题（8）的解为

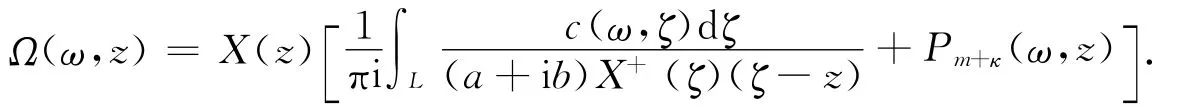
又因为

则可知，Ω（ω，z）在∞处以概率1有0阶极点（即m＝0）.从而可得

又因为

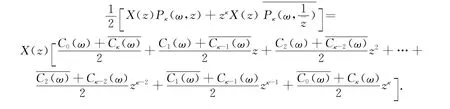
由此可得，随机Hilbert问题（1）的一般解为

（ii）当κ＜0时，由文献［2］可知，当且仅当满足条件

时，随机Riemann问题（8）有惟一解，所以可得

此时Pκ（ω，z）≡0，随机 Hilbert问题（1）有惟一解，即

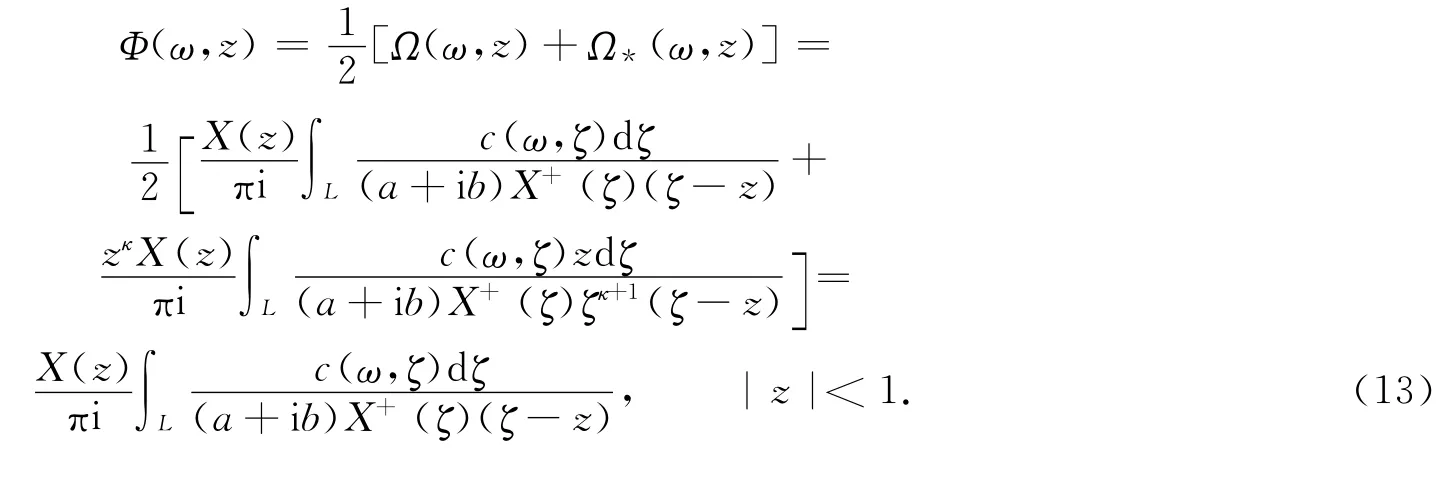
于是可得如下定理.

定理2 当κ≥0时，随机Hilbert问题（1）有一般解，即式（11）；而当κ＜0时，当且仅当满足条件（12）时，问题（1）有唯一解，即式（13）.

［1］WANG Chuan－rong.Random singular integral of random process with second order moment［J］.Acta Mathematical Scientia，2005，25B（2）：376－384.

［2］WANG Chuan－rong.Random singular integral and its application［M］.New Jersey：World Scientific Publishing Company，2000：191－197.

［3］林峰.Beurling－Ahlfors扩张的伸张函数的边界极限［J］.华侨大学学报：自然科学版，2004，25（4）：352－355.

［4］武宝亭，李庆生，杨跃武.随机过程与随机微分方程［M］.北京：电子科技出版社，1994.

［5］路见可.解析函数边值问题［M］.2版.武汉：武汉大学出版社，2004.

Random Hilbert Boundary Value Problem with Second Order Moment

YAO Cun，LIN Feng
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

In order to solve the random Hilbert boundary value problem of random process with second order moment，we convert it into randon Riemann boundary value problem by the method of symetrical expansion，and get its solution.

boundary value problem；Hilbert problem；Riemann problem；second order moment；symetrical expansion；random process

陈志贤 英文审校：张金顺，黄心中）

O 175.8

A

1000－5013（2011）06－0714－04

2010－07－12

林峰（1962－），男，副教授，主要从事函数论的研究.E－mail：lfeng＠hqu.edu.cn.

福建省自然科学基金资助项目（2007J0183）