在数学概念教学中提高学生的思维能力

朱益明

（大连市中山区青云小学,辽宁 大连 116001）

在数学概念教学中提高学生的思维能力

朱益明＊

（大连市中山区青云小学,辽宁 大连 116001）

指出了数学概念在小学数学中的重要地位,阐述了通过数学概念教学提高学生思维能力的具体策略。

小学;数学概念;思维能力

小学数学课程标准指出:“小学数学中的概念、公式、数量关系、解题方法等都是基础知识,必须使学生切实学好。”小学数学中包含大量的数学概念。数学概念是客观事物在数与形方面的抽象,是客观事物的数量关系和空间形式本质属性的反映,是学生理解知识、掌握知识、运用知识、培养能力的基础,是构建数学知识大厦的基石。数学概念在小学数学中占有极其重要的地位,因此,在小学数学教学中要加强概念教学,通过概念教学提高学生的思维能力。

一、丰富感知,理解概念,培养学生的抽象概括能力

小学生对事物的认识总是由感性发展到理性的,感官参与认识活动越多,所得到的感性材料越丰富,上升到理性认识就越全面、越深刻。教师只有把学生所有感官尽可能都调动起来,让学生用眼仔细看,用耳仔细听,独立思考,用手多做多练,才能使学生从不同的角度感知外界的各种信息。获得丰富的感知材料是建立正确概念的基础。

1.进行实验操作,抽象出概念

数学教学是数学活动的教学。实验操作过程是一个手、脑、口并用的过程,在学习中起着十分重要的作用,教师要充分借助直观的实验操作抽象出概念,使学生更好地理解概念的内涵。例如,体积是一个比较抽象的概念,小学生不容易掌握,在教学时教师可让学生动手做实验:（1）把一块石头放入有水的杯中,让学生观察水面会发生什么变化,并分析其原因。（2）把杯子装满大米,然后再把杯子里的米倒出放到一边,然后取2块大小不等的木块分2次放入杯中,再把倒出的大米装回杯子,让学生观察会出现什么情况,并思考其原因。学生经过操作实验、思考、讨论、交流,会发现木块、石头等物体都占有一定的空间。这时教师可因势利导,引导学生明确物体所占空间大小不同,有大有小,从而抽象出体积概念,即“物体所占空间的大小叫做物体的体积。”进行这样的直观性操作实验,不仅能使学生记忆深刻,而且有利于培养学生的抽象概括能力和探索问题的能力。

2.利用直观教学,理解概念

新课程标准明确指出:“数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。”在教学中教师要通过实物教具或实例引导学生正确理解所讲的概念。小学生年龄小,形象思维占主导地位,而直观教具具体、形象、生动、鲜明,容易感知,所以,讲授抽象的概念宜于运用直观教学。如“分数与除法的关系”内容中有这样一道练习题,要求学生比较“1吨的3/5”和“3吨的 1/5”的大小,学生感到难度很大,特别是思维能力较差的学生更觉吃力,教师可充分利用直观线段图帮助学生解决这个问题。（见图1和图2）

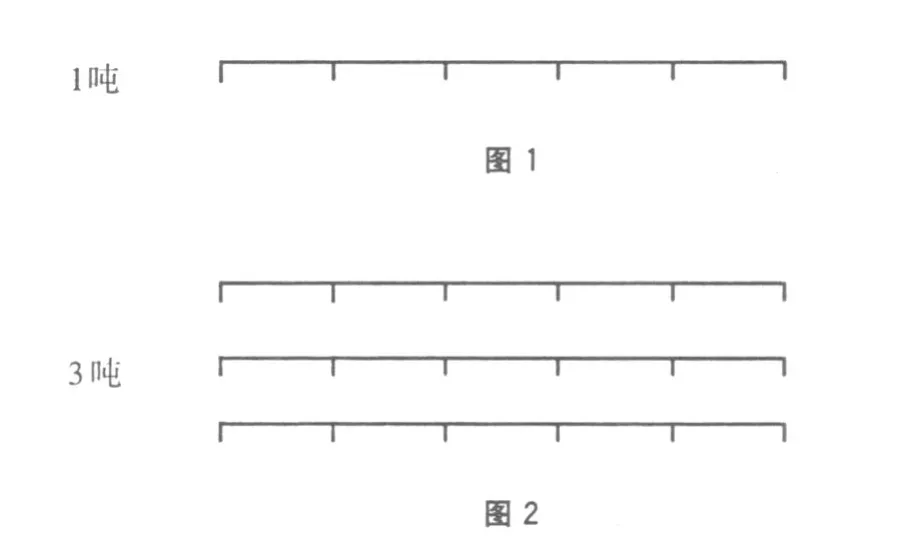
由此说明1吨的3/5就是1个3/5,即3/5吨,而3吨的1/5就是3个1/5,也是3/5吨,从而可以得出“1吨的3/5”和“3吨的1/5”是相等的。

直观教学是数学概念性知识教学的必要手段,不仅能帮助学生形成内容的表象,还可以调动学生学习的积极性。但也要明确,直观教学仅仅是一种手段而不是目的,所以使用时要适时、适度。

二、加强比较,鉴别概念,培养学生的分析和比较能力

数学概念之间既有密切联系又有严格区别,讲授新的概念时一定要重视和已有概念进行比较,使学生在探讨概念之间的联系和区别中掌握概念的本质,正确理解概念。

1.弄清差异,明确概念

明确概念就是对概念的内涵和外延都有一个清楚的了解。所谓概念的内涵就是概念所反映的事物的本质属性,而概念的外延是概念所指的对象的全体。只有弄清概念的差异,对概念的外延掌握全面,对概念内涵掌握准确,才能真正理解概念。有比较才有鉴别,比较是数学教学中的重要方法。在学习质数、互质数时,为了使学生深刻理解质数、互质数的概念并区分它们,可以提出这样的问题:在1至10这几个自然数中,哪几个数是质数?哪几对数是互质数?把它们一一列出,并进行比较。学生通过思考、交流会发现,质数本身是一个数,它可以独立存在,而互质数是成对出现且是互相依存的,这是内涵的区别。再进一步比较可以发现,两个不同的质数一定是互质数,但互质的两个数不一定都是质数,这是外延的区别。

2.新旧对比,讲解概念

讲授空间与图形这一部分新的概念时,要和有关的旧概念进行比较,弄清它们的区别和联系。如学习梯形时,教师可以将其与学过的平行四边形进行比较,找出它们的相同点和不同点。通过观察、讨论,学生会发现:两个图形都是四边形,两组对边分别平行且相等的是平行四边形;只有一组对边平行的是梯形。通过新旧之间基本图形的比较、判断等练习,既能巩固平行四边形的概念,又可建立“梯形”这个新概念,而且能提高学生的观察比较能力和分析鉴别能力。

三、反复实践,巩固概念,提高学生解决综合问题的能力

有数学专家曾说过,我们看一个少年儿童的数学才能,不是看他学过多少甚至背过多少数学知识,而是要看他在掌握的知识范围内解决问题的能力如何。学生学习了概念之后,必须通过实践,综合运用学习的知识去分析解决生活中的实际问题,这样概念才能被学生深刻理解和牢固掌握。所以在教学时教师要循序渐进,为学生设置问题情境,让学生先进行基本练习,即简单训练,以明确概念,理解概念,掌握概念;然后再进行综合训练,运用所学知识去解决较复杂的综合性问题。这类练习思维难度较大,但它既能使学生深刻理解概念,又能举一反三,进而培养学生解决综合问题的能力。如在讲完“长方体表面积”这一概念之后,首先进行基本练习,求长方体六个面的总面积（长方体的表面积）;其次进行变化练习,让学生观察没有盖的长方体纸盒并思考、讨论它的表面积的算法;再次进行解决实际问题的练习,如求一个没有盖的长方体形状的铁皮水桶需要用的铁皮;最后再进行较为复杂的问题的练习,如计算粉刷教室顶棚和四周墙壁（扣除门窗）的面积。通过这样层层递进式的练习,学生能够进一步加深对概念的理解和掌握。

Enhancing Mathematical Concepts Teaching and Improving Students’Thinking Ability

ZHU Yi-ming

（Qingyun Primary School of Zhongshan District,Dalian 116001,China）

The importance of mathematical concepts in primary mathematics is pointed out;specific strategies for imp roving students’thinking ability through teaching mathematical concepts are expounded.

primary school;mathematical concept;thinking ability

G632.3

A

1008-388X（2011）02-0055-02

2011-01-07

朱益明（1968-）,女（满族）,辽宁大连人,小学高级教师。

阅力]