复合平面曲线位置公差等效变换算法

闫 冠，侯 磊，邹飞舟，庄宇华

（1.吉林大学机械学院，吉林长春 130022；2.长春奥普光电技术股份有限公司，吉林长春 130033；3.长春市热力（集团）有限责任公司，吉林长春 130031）

复合平面曲线位置公差等效变换算法

闫 冠1，侯 磊1，邹飞舟2，庄宇华3

（1.吉林大学机械学院，吉林长春 130022；2.长春奥普光电技术股份有限公司，吉林长春 130033；3.长春市热力（集团）有限责任公司，吉林长春 130031）

根据公差原则的基本思想，以误差控制功能的等效性和公差带边界曲线的连续性为准则，建立了复合平面曲线图样尺寸公差与曲线位置公差的变换算法，从而为复合型廓形曲线的位置误差检测奠定了基础.

复合平面曲线；位置公差；等效变换；算法

轿车车身覆盖件、车轮轮辋、成形模具等有许多零件，具有较为复杂的表面形状，在生产图样中常以视图、剖视图的方式予以表达［1］，再基于尺规制图中所提出的要求，用样板进行检测［2］.对于制图中的剖面与曲面的截交线即所谓廓形曲线通常是由多段圆弧和直线首尾相切组合而成的复合平面曲线，在图样中通过标注一组结构尺寸和尺寸公差的方式来控制廓形曲线的实际形状和位置［3－7］.随着工业检测技术的进步，人们希望能够把坐标值测量原理和微机数据处理技术应用于廓形曲线的检测，以代替样板检测法.其技术关键在于寻找一种有效的变换算法，将图样中的尺寸公差集变换成廓形误差评定的依据.本文着重探讨复合平面曲线位置公差等效变换的变换算法以及相关技术问题.

1 基本概念与变换准则

根据在生产图样中廓形曲线的标注方式，各组成线段适合以参数方程形式描述.

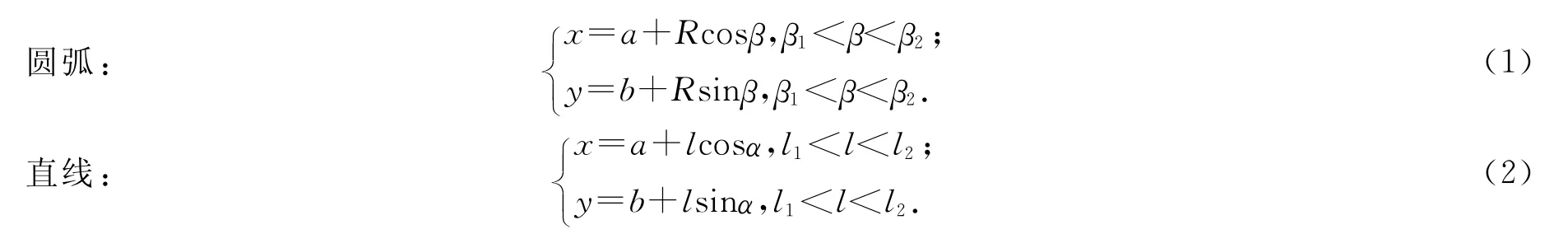
式中：a，b为给定点的定位尺寸；R为圆弧半径；α为直线倾斜角（逆时针为正）.相应的尺寸公差分别为2δa，2δb，2δR和2δα；β为动点相位角（逆时针为正）；l为动点到给定点的距离.依据几何关系，容易求出线段的端点参数β1，β2，l1和l2，在图样中通常按尺寸公差s和上、下偏差e1与e2的方式标注尺寸，可按（3）式将尺寸项改变成对称偏差的形式即t±δ，并将t称为理论正确尺寸.

虽然生产图样中对廓形曲线只标注尺寸公差，这种标注形式应理解为它的几何即形位误差是以尺寸公差集的形式控制的，所谓公差变换就是将图样尺寸公差集变换为曲线几何公差带.首先，将由理论正确尺寸决定的廓形曲线称为理论正确曲线，将理论正确曲线视为一动点M（x，y）在坐标平面xoy中的轨迹，将动点M的法向位置度定义为曲线位置度.廓形误差主要是指被测要素各个测点｛x i，y i｝至理论正确曲线的法向偏移量，廓形曲线的检测主要是测量实际曲线的坐标值并检验其是否超出了曲线位置度公差带.

公差变换的基本思想源于尺寸公差与几何公差的相关原则.然而，实践表明，直接按包容原则构造出的曲线位置度公差带是超宽的，会明显增加产品的误收率.因此，本文提出等效变换准则，强调变换前后2种公差形式对廓形误差的控制功能等效.其等效性的含义是设X，Y和Z为3个彼此独立且服从0均值随机正态分布的尺寸误差X－N（0，σ2x），Y－N（0，σ2y），Z－N（0，σ2z）.根据随机误差理论可知，变量U＝X＋Y＋Z服从N（0，σ2u）的正态分布且有σ2u＝σ2x＋σ2y＋σ2z.设2δx，2δy和2δz是三项尺寸公差，并假定它们是按拉依达准则制定的，即δx＝3σx，δy＝3σy，δz＝3σz.那么，它们的合成公差就满足δu＝3σu＝于是，变量U的公差带边界与尺寸误差X，Y和Z公差带边界所控制的误差概率相一致，都等于99.73%.

如前所述，廓形的理论正确曲线是光滑的.从目前实际产品的成形工艺看，实际廓形曲线也应该是平顺的.因此，本文提出公差变换的连续性准则，要求通过公差变换求得曲线位置度公差带的内外边界是连续曲线，也就是说，相邻线段的切点法向位置度相等.

2 圆弧位置度公差的变换结果

2.1 已知圆弧位置度公差的变换

这类圆弧可称之为独立圆弧，如图1所示.设M是理论正确圆弧上的任意一点，其相位角等于β.在径向线上取一点E（a＋Δa，b＋Δb）.Δa和Δb为尺寸误差.则E点对中心点A的偏移量为ΔE＝ Δacosβ＋Δbsinβ.对M点而言，β为常量，Δa和Δb为相互独立的随机变量.设2δe是圆弧中心点的位置度.按上述等效性准则有

由（4）式可知，2个中心定位尺寸的矩形公差带按等效性准则变换为一个与之内切的椭圆形点位置度公差带.做2条垂直于径向线的直线与椭圆相切.将两切点所在的椭圆通径定义为中心点A在径向线方向上的位置度，记为2δe.显然，当圆弧半径为理论正确尺寸时，M点的法向位置度等于2δe.若圆弧半径的尺寸公差为2δr，此时M点的法向位置度记为2δc，按上述等效性准则有

图1 圆弧位置度计算用图

2.2 连接圆弧位置度公差的变换

这类圆弧通过与两侧相邻线段相切而定位，其R，δr，β1和β2为已知.其端点法向位置度2δc（β1）和2δc（β2）等于相邻线段在切点处的位置度，假设已求出.设未知的中心点尺寸公差为2δa和2δb，由（5）式可知：

导出δ2a和δ2b的表达式后，再代入（5）式可得

由（6）式可知，连接类圆弧的位置度与其自身的半径公差无关.完全取决于两侧相切线段切点的位置度.可见，图样标注的半径公差只用于确定其形状公差即所谓圆弧曲度.

2.3 中间圆弧位置度公差的变换

这类圆弧通过与一侧相邻线段相切而定位，也可称之为半独立圆弧.实际上，（6）式中的δc（β1）和δc（β2）可理解为圆弧上任意两点的法向位置度，设β2为切点相位角，图样中给出圆弧上离y轴最远点x坐标和它的法向位置度2δcx，该点相位角βx＝0.代入（6）式得

同理，若已知δc（β1）和δcy（βy＝90°），（6）式变为

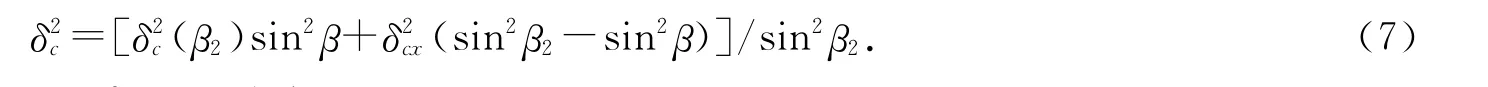
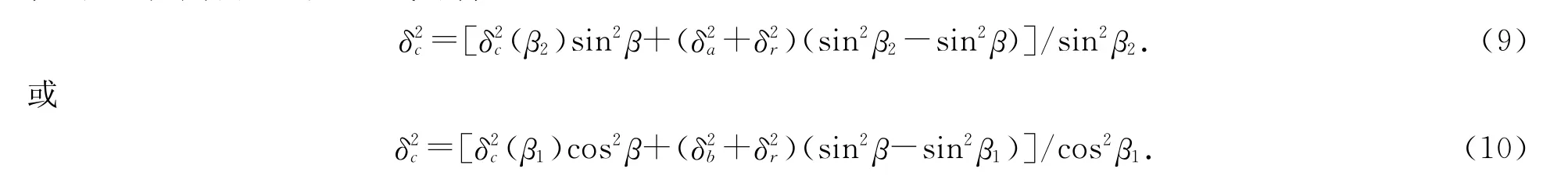
若圆弧除借助于一个切点定位外，图样中还给出一个中心定位尺寸和尺寸公差以及圆弧半径和半径公差时，则由（7）和（8）式可得

3 直线段位置度公差的变换结果

3.1 已知线段位置度公差的变换

这类直线段3个尺寸均为已知，称之为独立直线.如图2所示，首先将给定点2个定位尺寸的矩形公差带等效变换为椭圆公差带，做直线的2条平行线与椭圆相切.两切点所在椭圆通径定义为倾角0公差时的直线法向位置度2δe1.显然有

图2 直线位置度计算用图

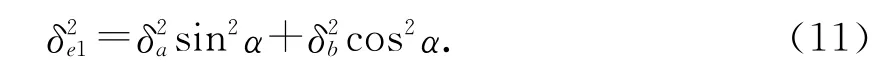
定位尺寸a与b为0公差时，单纯由倾角α的公差变换得到的直线位置度2δe2为

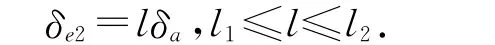
依据等效性准则，直线段的位置度2δl可由（12）式表示

3.2 连接线段位置度公差的变换

这类线段通过与两侧相邻圆弧相切而定位，是2条已定位圆弧的公切线，称之为连接线段.其理论正确曲线的端点参数l1和l2可由相切关系求出.两端点法向位置度2δl（l1）和2δl（l2）已知.任意点M的法向位置度2δl按线性插值法求出

3.3 中间线段位置度公差的变换

中间线段通过与一个相邻圆弧相切而定位，因为切点在直线上，作为给定点且l1＝0，其法向位置度2δe为已知.类比（12）式可得

4 关于复合平面线位置度概念的进一步讨论

一段圆弧或直线在坐标平面中的位置，不仅取决于给定点A的定位尺寸，也取决于半径或倾角.那么，从理论的严密性考虑就没有理由不把半径和倾角作为曲线的定位尺寸.在曲线位置度的变换式中，理应引入半径公差和倾角公差.然而，曲线位置度的内涵并不是单纯的理论问题，更重要的是它还取决于产品的设计规范、制造工艺、检测方法和使用效果.因此，本文将在公差变换式中不计入半径公差和倾角公差的位置度称为复合平面曲线的Ⅰ型位置度.而将计入两项公差的位置度称为复合平面曲线的Ⅱ型位置度.到目前为止，没有关于复合平面曲线变换的文献报道.现行产品的技术文献通常是建立在尺寸公差与样板检测的基础之上的.我们认为，Ⅰ型位置度大体上与应用光滑极限量规定对重点标注尺寸逐项进行检测的技术规范相一致.而Ⅱ型位置度大体上与应用整体式标准样板（充分接近理论正确曲线的样板）进行综合检测的技术规范相一致.例如，汽车轮辋以按Ⅰ型位置度检测为宜，而轿车轮辐以按Ⅱ型位置度检测为宜.

5 实例研究

汽车轮辋的轮缘曲线是一条很有代表性的复合平面曲线.如图3所示，它由胎圈座直线、胎圈座圆弧、轮缘侧直线和轮缘圆弧等4条线组成.取标注尺寸及尺寸偏差：轮辋半宽度w＝（70±1）mm，槽深h＝（18±0.1）mm，轮缘高度g＝（19.5±0.5）mm，胎圈座角度θ1（5±1）°，轮缘侧直线倾角θ2＝（90±2）°，胎圈座圆弧半径R2＝（6.5±1）mm，轮缘圆弧半径R4＝（9±0.5）mm，端点尺寸p＝20 mm，q＝12 mm.廓形检测时以轮辋对称线y轴和槽底直线x轴为测量基准.首先，将各线理论正确尺寸及端点参数计算出来并列于表1.根据各线类型，将轮缘曲线的Ⅱ型位置度计算结果列入表1.

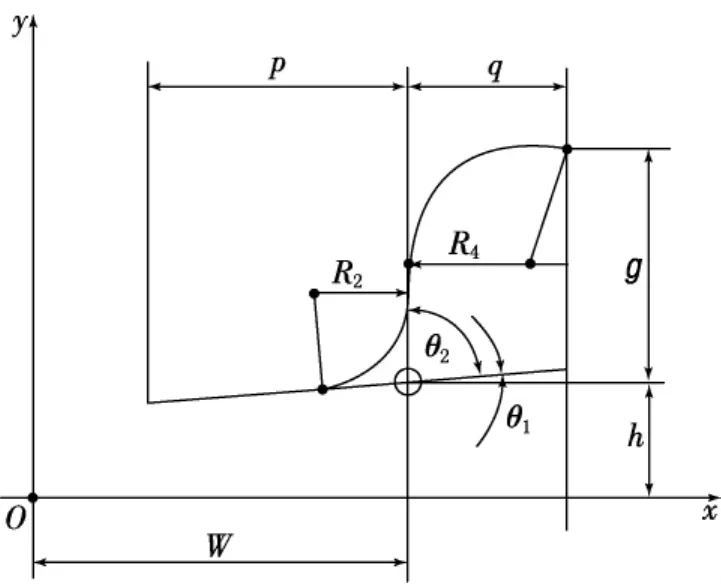
图3 汽车轮辋轮缘曲线

表1 计算的理论正确尺寸、尺寸公差、端点参数、端点法向位置度

［1］侯洪生.机械工程图学［M］.北京：科学出版社，2008：196－212.

［2］国家技术监督局.GB／T9769－2005轮廓轮辋检测［S］.北京：中国标准出版社，2005：1－11.

［3］甘永立.形状和位置误差检测［M］.北京：国防工业出版社，1995：27－49.

［4］梁晋文.误差理论与数据处理［M］.北京：中国计量出版社，1989：1－11.

［5］甘永立.几何量公差与检测［M］.上海：上海科学技术出版社，2010：30－115.

［6］陈于萍.互换性与测量技术基础［M］.北京：机械工业出版社，2006：6－92.

［7］齐新丹.互换性与测量技术［M］.北京：中国电力出版社，2008：7－117.

Transformation algorithm between the size tolerances and the position tolerance on the plane compound contour

YAN Guan1，HOU Lei1，ZOU Fei－zhou2，ZHUANG Yu－hua3
（1.College of Mechanical Science and Engineering，Jilin University，Changchun 130022，China；2.Changchun UP Optotech Company Limited，Changchun 130033，China；3.Changchun Thermal Group Company Limited，Changchun 130031，China）

According to the tolerance principle，by means of the equivalent criterion of the controlling function and the continuity of the tolerance margin，a transformation algorithm between the size tolerances and the position tolerance on the contour is advanced in this paper.Therefore the mathematical basis is provided for data processing of the coordinate values measured of the plane compound contour.

plane compound contour；position tolerance；transformation；algorithm

TG801

460·2030

A

1000－1832（2011）04－0054－05

2011－06－05

吉林省科技发展计划项目（20090202）.

闫冠（1965—），女，副教授，主要从事画法几何、工程图学及测量学研究；通讯作者：侯磊（1965—），男，硕士，副教授，主要从事材料表面精加工及精密测量研究.

石绍庆）