万向接轴损伤的灰色识别与预测分析

张松鹤，包 耳

(大连民族学院a.土木建筑工程学院;b.机电信息工程学院，辽宁 大连 116605)

万向接轴损伤的灰色识别与预测分析

张松鹤a，包 耳b

(大连民族学院a.土木建筑工程学院;b.机电信息工程学院，辽宁 大连 116605)

以反映结构损伤程度的固有频率作为损伤识别的特征参数，应用可以同时反映多种特征参数影响的灰色GM(1，n)模型对万向接轴的损伤问题进行了识别和预测分析。为提高预测精度和准确性，根据结构的固有频率随损伤程度的变化规律，采用了对原始数据进行归一化和二次累加处理的方法。通过识别实例表明，采用此方法对工程结构进行损伤特征识别分析能够取得较好的效果，为结构损伤识别和预测提供了新方法。

灰色GM(1，n)模型;万向接轴;固有频率;损伤识别;预测

灰色系统理论是由邓聚龙教授于1982年提出［1］，经过几十年的发展，灰色系统理论在系统分析、系统建模、灰色预测、灰色决策和灰色控制等方面都取得了长足的进步，同时在工业、农业、经济、气象、商业、医学、故障诊断等众多领域也得到了广泛的应用。在结构损伤领域，结构一旦出现损伤，会影响到结构的各种静动态参数，比如静态位移曲率、固有频率和损伤系数等［2－4］，而且对这些参数的影响规律也表现出复杂的非线性关系。已有一些学者利用灰色预测理论对结构损伤和剩余寿命问题进行了识别和预测分析研究［5－7］，但都是基于灰色GM(1，1)模型。GM(1，1)模型只能针对一种特征参数或特征参数中的某一组因素进行预测，并不能反映出各种(多组)因素的相互影响。本文提出以结构损伤的各阶固有频率作为特征参数，利用可以同时反映多种特征参数影响的GM(1，n)模型对结构损伤识别和预测问题进行分析和研究，取得了较好的效果。

1 GM(1，n)模型

GM(1，n)模型是系统协调模型，是解决系统的各因素之间动态协调的工具，可利用它来观察系统的各项敏感因素的变化对系统状态的影响程度，分析系统各敏感因素的区域敏感势态与各变量间的关系，进而确定系统在未来发展中各因素的状态，并对因素的不协调进行调整［8］。

设有各因素的原始序列为

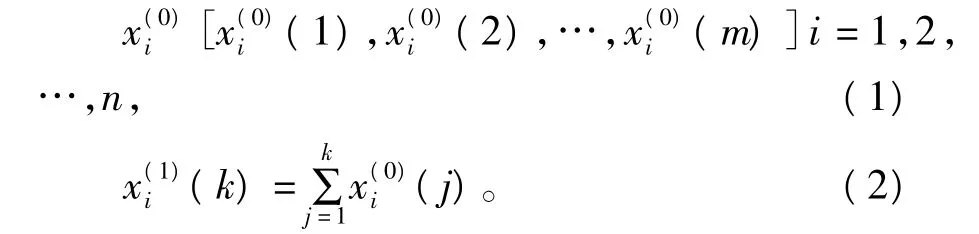
式中，b2，b3，…，bn反映了系统各因素与主因素之间的动态关联程度;bi＞0表示该因素i对主因素有促进作用，bi＜0表示该因素i对主因素有阻碍作用;a值则反映主因素和各因素之间的协调程度，a＞0表示不太协调，a越大，则不协调程度越大。

微分方程的参数 a，b2，b3，…，bn可用最小二乘法求解:+－为

2 损伤识别实例

这里采用文献［9］中小型轧机万向接轴裂纹损伤的实测数据，以万向接轴损伤的前4阶固有频率为特征参数进行损伤的灰色预测分析。首先为保证样本数据的等间隔性，对数据进行了间隔插值处理;其次对损伤程度值和特征参数进行了

由此得结果见表1。由于结构的固有频率随损伤程度的增加总体上呈现出下降的趋势，为保证数据的递增规律，提高预测精度，在此提出对特征参数进行二次累加处理，即

由式(13)得到累加生成灰色模块，见表2。

表1 万向接轴损伤程度与其前4阶固有频率的关系

表2 累加生成结果

确定数据矩阵X和Y:

由式(14)结果可见，a=1.9230，说明各阶固有频率的协调性尚可。b2和b3均小于零，说明第1和2阶固有频率对结构损伤有阻碍作用，即其敏感性要弱一些;b4和b5均大于零，说明第3和4阶固有频率对结构损伤有促进作用，即其敏感性要更强一些，这也再一次验证了结构损伤与其固有频率的关系，即高阶固有频率比低阶固有频率对损伤更为敏感［9］。

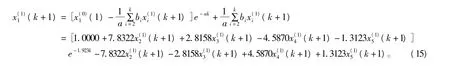
由此得GM(1，n)模型的微分方程为

由式(15)得到预测值，见表3。

表3 模型还原值与误差

进行后验差检验，利用式(9)求得e和x的方差为

根据 p＞0.95 和 C ＜0.35 的标准［8］，表明所得的预测结果较好。

3 结论

(1)结构出现损伤对结构的各阶固有频率都会产生影响，应用GM(1，n)模型可以分析各种因素(各阶频率)对损伤的影响程度，确定损伤预测中各因素(各阶频率)的状态，从损伤识别实例可见，采用此方法对工程结构进行损伤特征识别分析能够取得较好的效果。

(2)损伤识别和预测中最大误差是12.91%，从灰色理论角度，误差偏大的原因可能是由于其属于识别预测中早期的数据，数据越早，对灰色模型的影响就越弱，识别的结果的误差也会更大，因此建模时应及时去掉老数据，补充新数据。从结构损伤特征角度，其对低阶固有频率敏感性差。因此还原结果误差也偏大。识别和预测结果中整体的平均误差为3.92%，完全满足精度和准确度的要求。

(3)鉴于结构的各阶固有频率随损伤程度的变化规律，应对原始数据进行必要的处理，如均值化、归一化及多次累加生成等进行处理，以保证识别和预测的精度和准确性。

［1］邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1990.

［2］陈孝珍，朱宏平，陈传尧.灰色相关性分析在结构静力损伤识别中的应用［J］.力学与实践，2005，27(3):60－64.

［3］薛松涛，钱宇音，陈镕，等.应用灰色关联度分析检测结构损伤的位置和程度［J］.振动与冲击，2005，24(1):66－69.

［4］李建民，孟庆霞.灰色系统理论在舰船装备剩余寿命预测中的应用［J］.兵工自动化，2009，28(5):29－33.

［5］商怀帅，宋玉普，程万鹏，等.混凝土结构寿命的灰色预测［J］.黑龙江工程学院学报，2005，19(1):17－24.

［6］王技，钟海辉.灰色理论在桥梁剩余寿命预测中的应用研究［J］.现代交通技术，2006(3):36－38.

［7］田峻山，张帆，俞奇勇.混凝土结构寿命灰色的模型及预测［J］.华北科技学院学报，2007，4(2):57－59.

［8］严智渊，戴玉生.灰色系统预测与应用［M］.南京:江苏科学技术出版社，1989.

［9］虞和济，陈长征，张省，等.基于神经网络的智能诊断［M］.北京:冶金工业出版社，2000.

Analysis on Grey Identification and Forecast of Universal－shaft with Damages

ZHANG Song－hea，BAO Erb
(a.College of Civil and Architecture Engineering，Dalian Nationalities University;
b.College of Electromechanical and Information Engineering，Dalian Nationalities University，Dalian Liaoning 116605，China)

Taking the inherent frequencies as characteristic parameters of damage identifications，the identification and forecast of universal－shaft with damage have been analysed with grey GM(1，n)model.The GM(1，n)model can reflect the influences of manifolds characteristic parameters.For increasing the forecast precisions and veracities，the methods of normalization and accumulativeness has been adopted in the originality data processing based on the changing rules of the inherent frequencies with damage degree.The results show that it obtains perfect results on damage identification in engineering structures by the method.The new method is provided for identification and forecast of damage in structures.

grey GM(1，n)model;universal－ shaft;inherent frequency;damage identification;forecast

TU323.5

A

1009－315X(2011)05－0486－04

2011－06－27;最后

2011－07－10

张松鹤(1964－)，女，辽宁沈阳人，工程师，主要从事结构与设备故障的智能诊断、结构强度计算等。

(责任编辑 邹永红)