基于MODIS地表参数产品和地理数据的近地层气温估算方法评价——以安徽省为例

曲培青，施润和，刘朝顺，钟洪麟

(1.华东师范大学地理信息科学教育部重点实验室，上海 200062;2.华东师范大学，中国科学院对地观测与数字地球科学中心环境遥感与数据同化联合实验室，上海 200062)

基于MODIS地表参数产品和地理数据的近地层气温估算方法评价
——以安徽省为例

曲培青1，2，施润和1，2，刘朝顺1，2，钟洪麟1，2

(1.华东师范大学地理信息科学教育部重点实验室，上海 200062;2.华东师范大学，中国科学院对地观测与数字地球科学中心环境遥感与数据同化联合实验室，上海 200062)

为研究应用MODIS地表参数产品估算近地层气温的可行性，对MODIS地表温度(LST)、反照率(ALBEDO)、植被指数(NDVI)等产品数据和高程(ALT)、纬度(LAT)等地理数据进行主成分分析，并以主成分累积方差较大的前若干个主成分作为自变量，建立自变量与各气象台站气温之间的多元线性关系。结果显示:所建立的多元线性回归模型的均方根误差(RMSE)均在0.5～2.4之间，其中，与月平均最高气温(Tmax)和14时气温(T14)回归得到的RMSE整体较大，与月平均最低气温(Tmin)回归得到的RMSE整体较小;RMSE的波动呈现出冬季大、夏季小的季节特征;利用Terra/MODIS数据得到的结果优于利用Aqua/MODIS数据得到的结果，且其夜间数据对Tmin的估算精度较高，日间数据对Tmax和T14的估算精度较高;各参数对气温回归权值影响从大到小依次为LST、ALT、LAT、NDVI和ALBEDO。因此，利用MODIS地表参数产品可以监测不同时刻的近地层气温空间分布，但对不同时刻的气温回归分析，最优数据选择有所不同。

气象台站;气温;MODIS产品;精度评价

0 引言

近地层气温是全球气候变化研究的关键指标之一，对其进行精确的定量反演具有重要的科学价值。目前，大量近地层气温资料均由气象台站实测获得。但由于气象台站呈点状分布，所以只有对其获得的数据进行插值等处理才能获得空间连续的气温信息。而插值处理往往会带来一些不确定性，这便影响和限制了区域气温信息的准确获取和利用，该问题在气象台站分布稀疏的地区尤为突出。

利用卫星遥感的热红外波段数据反演气温一般采用“两步走”的方式，即首先利用遥感数据反演地表温度(LST)，然后再由LST数据推导出气温值。由LST数据推导气温的方法一般分为模型法和经验法两种，前者须获取作物水分胁迫指数和空气动力阻力等参数［1］，而这些参数通常难以直接获得，因此限制了该方法的应用范围;后者是通过建立气温与相关遥感或地理参数之间的函数关系来实现的，常见的有温度植被指数法和统计学方法。温度植被指数法假设在一定植被覆盖度下的植被辐射温度与周围空气温度相当，利用植被指数和地表温度的负相关性获得研究区内的气温［2－4］，但不同地区、不同季节以及不同传感器获得的植被辐射温度与周围空气温度相当的植被指数并不同［3，5］，且该方法在植被稀疏区不适用;统计学方法则直接建立气温与LST的函数关系(多为线性关系)。Vogt等［6］建立了日最高气温和LST的线性回归关系，得出平均误差在2～2.5 K之间;Yan等［7］通过建立不同纬度的校正方程对回归结果进行校正，使估算精度有一定提高;Cristobal等［8］建立了遥感数据和气象台站地理数据与气温的多元线性关系，认为这两类数据的应用可以有效改善回归模型的精度;Vancutsem等［9］通过分析MODIS的LST产品与气温的线性关系，认为MODIS夜间数据可较好地估算最低气温，而白天数据与最高气温的关系不稳定。

为了进一步研究利用MODIS地表参数产品估算近地层气温的可行性和适用性，本文以安徽省2003—2005年数据为例，以月平均气温、月平均最高气温、月平均最低气温以及每天2时、8时、14时、20时这4个瞬时气温为研究对象，利用多元线性回归方法评价和分析MODIS地表温度(LST)、反照率(ALBEDO)、植被指数(NDVI)等地表参数产品和高程(ALT)、纬度(LAT)两种地理数据对上述气温估算的精度及其规律。

1 数据源

1.1 气象站点数据

本文所使用的安徽省80个气象站点(图1)数据包括气象站的纬度、高程等地理数据和2003—2005年间的常规气温数据。气温数据包括月平均气温、月平均最高气温、月平均最低气温以及每天4个时刻(2时、8时、14时和20时)的观测气温数据。

图1 安徽省气象站点分布Fig.1 Location of meteorological stations in Anhui province

1.2 遥感数据

本文采用的MODIS产品数据包括Aqua和Terra星每8 d合成的LST产品、每16 d合成的ALBEDO产品以及每月合成的NDVI产品，这些产品均从NASA 相关数据发布网站(https://wist.echo.nasa.gov/)获得。

2 研究方法

2.1 数据预处理

2.1.1 气象站点数据的预处理

首先计算2003—2005年间每天4个时刻的月平均气温数据，即2时月平均气温(T02)、8时月平均气温(T08)、14时月平均气温(T14)和20时月平均气温(T20);然后将这4个时次的气温与月平均气温(Tmean)、月平均最高气温(Tmax)、月平均最低气温(Tmin)的时间尺度进行统一。

2.1.2 遥感数据的预处理

首先对研究区的遥感数据进行投影转换和拼接，提取出气象站点处的遥感地表参数数据，即LST、NDVI和 ALBEDO，并根据文献［9］把连续两个8d内LST差值超过6℃的异常值删除，最后将8d合成的LST产品和16d合成的ALBEDO产品均处理成月产品。

2.2 回归分析

利用多元线性回归方法建立气温与遥感地表参数产品、气象台站地理数据之间的关系，从而分析和评价MODIS地表参数产品对气温的反演精度。自变量选取需考虑那些与气温密切相关的若干因子，包括各个气象站点的 LAT、ALT、LST、NDVI和ALBEDO; 因变量选取 Tmean、Tmax、Tmin、T02、T08、T14和T20。

由于Aqua和Terra卫星过境时刻不同，其反演的LST值存在较大差异。通过对LST进行细分，产生了不同自变量组合(表1)。

表1 自变量分组情况Tab.1 Groups of independent variables

为了消除自变量之间共线性的影响，在回归分析之前先进行主成分分析，选取主成分累积方差大于80%的前若干个主成分作为自变量进行回归分析，并采用逐步回归的方法自动选择自变量。对2003—2005年同一月份的样本数据逐月建立每个因变量的回归方程，共7组自变量、7类气温指标、12个月的样本数据。因此，最后生成的方程有7×7×12个，所有方程及其偏回归系数都通过0.05水平的显著性检验。

3 结果与分析

3.1 回归精度分析

以 2003—2005 年逐月 Tmean、Tmax、Tmin、T02、T08、T14和T20作为因变量，采用不同的自变量组合对近地层气温分别进行回归精度分析，其结果如表2所示。

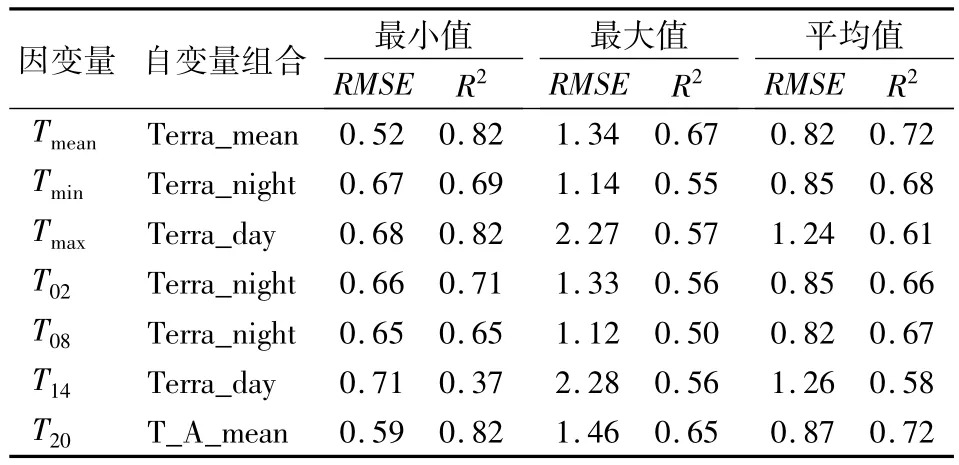
表2 2003—2005年气温回归模型精度统计Tab.2 Statistics of accuracy measurements of temperature regression model from 2003 to 2005

从表2可以看出，因变量 Tmean和 T08的平均RMSE最小，为0.82;而Tmax和 T14的平均 RMSE较大，均超过了1.20。日低温时段(如T02)的气温估算精度之所以优于高温时段(如T14)，主要是由于白天太阳辐射对地表能量平衡产生影响，使得对高温时段的气温估算精度降低。研究还发现，与Aqua/MODIS LST相比，Terra/MODIS LST对各因变量气温指标的估算精度略优，故表2中未列出与Aqua/MODIS LST相关的自变量组合及其统计结果。此外，Terra/MODIS晚上的LST对Tmin和T02的估算精度较高，而白天的LST对Tmax和T14的估算精度相对较高。

从以上分析还可以得出，近地层气温的估算精度受卫星过境时间的影响，即白天过境的卫星数据对Tmax和T14具有较高的估算精度，晚上过境的卫星数据对Tmin和T02等具有较高的估算精度。但研究发现，虽然Aqua白天过境地方时接近14时，晚上过境地方时接近02时，但其对T14和T02的估算精度均不是最高的，这可能与影响气温的因素众多以及LST反演精度等有关，有待进一步研究。

3.2 估算精度的月变化分析

分别选择对各气温类型逐月估算精度最佳的回归模型，分析其RMSE的月变化特征。从图2可以看出，所有气温类型的RMSE在0.5～2.4之间，各类气温指标在不同月份的RMSE变化特征不尽相同。多数类型的RMSE在冬春季各月中波动较大，如反映日高温状况的Tmax和T14，而在夏季较平稳，如反映日低温状况的Tmin。

图2 2003—2005年间气温回归模型的RMSE月变化Fig.2 Monthly RMSE variation of the temperatureregression model from 2003 to 2005

3.3 权值影响分析

为了研究各变量对气温估算精度的影响，本文对回归系数和载荷矩阵进行了分析。结果表明，标准化回归系数的绝对值越大，所对应的自变量对因变量的相对影响也就越大。也就是说，各个主成分的系数大小反映了自变量对因变量的影响程度，而主成分载荷矩阵则影响了原始变量的贡献大小。因此，载荷矩阵与标准化回归系数的乘积反映了原始变量对因变量的作用。选取各个气温类型回归精度高的模型，分析原始变量对气温的影响作用，如图3所示。

图3 2003—2005年气温回归模型中各自变量的权值Fig.3 Weights of different variables in air temperature regression model from 2003 to 2005

在所有月份、所有类型的气温回归分析中，气象台站的纬度和高程对气温有“负”的影响，平均大小分别在0.2和0.4附近。纬度(或高程)越高，气温就越低;纬度(或高程)越低，气温就越高。植被指数和反照率对近地层气温的影响较小，平均小于0.2。

LST与近地层气温的正相关性较为明显，相关系数在0.6附近波动。如果地表温度高，通过热量传输便可以把更多的热量输入大气，使近地层气温升高，反之，则使近地层气温降低。在Tmin和Tmean的回归分析中，LST的权值相对较大，大于0.6;在Tmax和接近最高气温(T14)的回归分析中，LST的权值相对较小，小于0.6，说明最高气温的影响因素比较复杂，更难估算。

在影响近地层气温的所有变量中，LST的影响作用最大，其次是 ALT、LAT、NDVI和 ALBEDO。这与Cristobal等［8］在加泰罗尼亚地区对136个气象站点进行月回归分析的研究结论基本相似，但各个变量对近地层气温的影响程度稍有不同。

4 结论

为了评价MODIS不同类型产品数据对近地层气温反演结果的影响，本文利用2003—2005年白天和晚上的LST、NDVI、ALBEDO遥感数据，并结合气象台站ALT、LAT地理数据，建立与气象台站地表观测气温的多元线性关系模型。通过7组数据对7种气温类型在12个月内的共588个回归方程的分析，得出如下结论:

(1)将MODIS白天和晚上4个时刻的遥感数据与气象台站地理数据相结合，可以监测不同类型近地层气温的空间分布，这对各种生态环境模型具有重要的应用价值。

(2)在不同类型的近地层气温回归分析中，所选择的最优数据有所不同。本研究为不同气温类型的反演提供了数据选择依据:反演平均气温时采用Terra白天和晚上的平均数据较好;反演最低气温、2时和8时气温时采用Terra晚上的数据较好;反演最高气温和14时气温时采用Terra白天的数据较好。

(3)从Terra数据对最高/最低气温的反演精度优于Aqua数据看出，最高和最低气温的反演精度受卫星过境时间的影响并不明显，但实时的气温反演需要时间效应。因此，对卫星过境时间对实时气温的回归模型影响还需进一步研究。

总体上，月平均气温回归获得的RMSE最小，月平均最高气温和14时月平均气温的RMSE较高。RMSE在时间上的变化表现为夏季月份波动小，冬季月份波动大。各个原始变量对气温的权值影响，表现为LST的影响最大，其次是ALT、LAT、NDVI和ALBEDO。但由于近地层气温受到多种因素的影响(如下垫面用地类型)，如何评估这种影响以及如何把这种影响加入到经验统计模型当中，将对近地面气温反演具有重要意义。

［1］Sun Y J，Wang J F，Zhang R H，et al.Air Temperature Retrieval from Remote Sensing Data Based on Thermodynamics［J］.Theoretical and Applied Climatology，2005，80(1):37 －48.

［2］Prince S D，Goward S N.Global Primary Production:A Remote Sensing Approach［J］.Journal of Biogeography，1995，22(4):815－835.

［3］Stisen S，Sandholt I，Nørgaard A，et al.Estimation of Diurnal Air Temperature Using MSG SEVIRI Data in West Africa［J］.Remote Sensing of Environment，2007，110(2):262 －274.

［4］Riddering J P，Queen L P.Estimating Near－ surface Air Temperature with NOAA AVHRR［J］.Canada Journal of Remote Sensing，2006，32(1):33 －43.

［5］Goward S N，Xue Y K，Czajkowski K P.Evaluating Land Surface Moisture Conditions from the Remotely Sensed Temperature/Vegetation Index Measurements:An Exploration with the Simplified Simple Biosphere Model［J］.Remote Sensing of Environment，2002，79(2):225 －242.

［6］Vogt J V，Viau A A，Paquet F.Mapping Regional Air Temperature Fields Using Satellite － derived Surface Skin Temperatures［J］.International Journal of Climatology，1998，17(14):1559 －1579.

［7］Yan H，Zhang J H，Hou Y Y，et al.Estimation of Air Temperature from MODIS Data in East China［J］.International Journal of Remote Sensing，2009，30(23):6261 －6275.

［8］Cristòbal J，Ninyerola M，Pons X.Modeling Air Temperature Through a Combination of Remote Sensing and GIS Data［J］.Journal of Geophysical Research，2008，113(D13):D13106.

［9］Vancutsem C，Ceccato P，Dinku T，et al.Evaluation of MODIS Land Surface Temperature Data to Estimate Air Temperature in DifferentEcosystemsoverAfrica［J］.Remote Sensing of Environment，2010，114(2):449 －465.

The Evaluation of MODIS Data and Geographic Data for Estimating Near Surface Air Temperature

QU Pei－ qing1，2，SHI Run － he1，2，LIU Chao － shun1，2，ZHONG Hong － lin1，2
(1.Key Laboratory of Geographic Information Science，Ministry of Education，East China Normal University，Shanghai 200062，China;2.Joint Laboratory for Environmental Remote Sensing and Data Assimilation，ECNU and CEODE，Shanghai 200062，China)

The main objective of this study is to discuss the feasibility of predicting near－surface air temperature using MODIS products.Principal component analysis of land surface temperature(LST)，ALBEDO，vegetation index(NDVI)，altitude(ALT)and latitude(LAT)was employed，with some principal components of the cumulative variance in the front of these principal components as independent variables.Multiple linear relationships between independent variables and meteorological observation temperatures were established.The results show that the range of RMSE is between 0.5 and 2.3.Most of RMSE vary greatly in winter months but are relatively stable in summer months.Compared with Aqua/MODIS，Terra/MODIS can get better results.RMSE of Tminmodeled by Terra nighttime MODIS is lower，and so are Tmaxand T14modeled by Terra daytime MODIS.LST is the most powerful predictor，followed by ALT，LAT，NDVI and ALBEDO.The MODIS products can therefore monitor the spatial distribution of near－ surface air temperature at different times，with the optimal products selections being different.

Meteorological station;Air temperature;MODIS products;Accuracy assessment

TP 79

A

1001－070X(2011)04－0078－05

2011－03－14;

2011－05－09

国家重点基础研究发展计划(编号:2010CB951603)和上海市科技支撑计划项目(编号:2010DZ0581600)共同资助。

曲培青(1984－)，女，主要研究方向为遥感应用和GIS应用。

施润和(1979－)，男，主要从事定量遥感研究。E－mail:rhshi@geo.ecnu.edu.cn

(责任编辑:刁淑娟)