利用局部集聚特性的聚类算法的研究

牛习现，赵立川

（1.河北青年管理干部学院信息技术与传播系，河北石家庄 050031；2.河北科技大学后勤集团，河北石家庄 050018）

利用局部集聚特性的聚类算法的研究

牛习现1，赵立川2

（1.河北青年管理干部学院信息技术与传播系，河北石家庄 050031；2.河北科技大学后勤集团，河北石家庄 050018）

基于SNN相似性和密度的聚类算法是当前主要的无监督聚类方法之一，该类算法在发现不同大小形状簇的聚类过程中都取得了较好的结果。但是该类算法也存在局限性，如Jarvis-Patrick算法通过单连结的方式发现簇，可能分割真正的簇或者合并应该保持分离的簇，而SNN密度类算法的Eps，MinPts参数的确定对用户来说是比较困难的。针对该类问题，本文对聚类过程中的局部集聚特征进行了分析和定义，提出了利用数据的局部集聚特征来控制聚类过程的的聚类算法。通过验证，该算法对发现不同密度以及任意形状的数据集合的聚类分析问题是有效的，突出了数据分析的局部集聚特征，改进了数据聚类的质量。

数据挖掘；聚类分析；局部集聚特性；SNN密度

聚类分析是人类的基本概念性活动之一，而人类自发的聚类分析过程通常是基于相对较少的选择属性进行的，并且不能排除人的偏见。因此当分析的对象集合是由相当数量的定量属性来修饰定义，并且想要获得无人为偏见干扰的分析结果时，就不可避免地使用了数学工具。但是数学工具的使用也具有局限性，因为数学工具的选择和解决方案都是由人选择和决定的，有特定的倾向性［1］。聚类分析是数据挖掘的方法之一，用来在无标识的数据集合中发现其内在结构和联系，将对象按照某方面的相似性进行组织分组的过程，因此每个聚类都是对象的集合，并且他们之间具有相对强的相似性，而不同聚类之间对象则具有相对较弱的相似性或者不具有相似性［2］。针对不同的数据类型、数据集合的大小、对象的属性个数以及想要发现聚类的类型等，相关研究人员设计实现了很多卓有成效的分析算法，其主要算法如下：K均值法、Chameleon法、STING法、SOM 法、SNN Density Based Methods法、Jarvis-Patrick法等聚类分析的方法［2－3］。本文的研究以 SNN密度和SNN相似性分析方法过程中数据局部集聚特征为基础，旨在通过对已有相关算法的研究分析，找出解决其局限性的途径，设计新的聚类算法，增强算法的适应性以及改进聚类分析的质量。

1 SNN相似性与SNN密度分析

通常将聚类分析定义成应用技术手段将对象集合分割成不同的分组，在同一分组中的对象比不属于同一分组中的对象具有更强的相似性，因此在这个意义上聚类是发现相互之间具有相似性的对象的分组过程。然而聚类的这种定义并不是通用的，在很多情况下让属于同一分组的对象相互之间具有较强的相似性并不是必须的，取而代之的是，这些对象之间表现出来较高的连接特性，它可以被认为是相互近邻的对象之间的关联属性，以相互连接或序列模式体现。因此一些并不具备直接相似性的对象被不间断的邻近的对象连接起来形成完整的集聚簇。进而可以得到更为一般化的聚类分析的定义，即它是一种通过给定的模型或相似性度量方法对异构不统一的项目集合进行确认同质子集的数据分析的技术。而这样的数据子集的特征定义可以通过SNN密度和SNN相似性来体现［1］。

在一些情况下，依赖于标准相似性和密度度量方法的聚类分析技术不能够产生合适的聚类结果，因此应该分析原因找到其他相似性的度量方法，通常可以认为，如果2个数据对象同时与许多共同的数据对象具有较高相似性，即使是通过直接的度量方法不能体现出它们之间具有相似性，那么它们之间也会具有较高的相似性，是因为对象之间的关系具有传递性。这正是SNN相似性度量的基础依据。SNN度量方法可以解决低相似性数据对象（如文档类对象集合）和密度分布不均匀数据集合的聚类分析问题［3］。SNN相似性计算的描述算法如下。

1）发现所有数据对象的k个最近邻居。

2）如果2个数据对象x和y不存在于对方的k个最近邻居列表中，则有：

similarity（x，y）＝＝0；否则similarity（x，y）＝＝共享邻居数。

由于SNN相似性度量方法反应了数据空间中局部数据对象的分布特性，并且该方法相对于数据空间中密度的变化以及维度的变化不敏感，使得它成为基于密度的度量方法的新选择。SNN密度方法给出了数据对象被相似对象包围的程度，因此数据对象所处区域的密度的高低变化是和SNN密度一致的。该类方法可以很好地适应具有较大范围密度变化的数据集合，同时仍然可以发现低密度的簇。依据SNN密度确定对象类别的方法描述如下。

核心对象：如果1个数据对象的邻居数在SNN相似性定义以及用户提供的参数Eps的条件下超出了另一个提供参数MinPts阈值，则标记该对象为核心对象。

边界对象：如果1个数据对象周围没有足够的邻居使它成为核心对象，但是却是某一个核心对象的近邻，这样的对象称为边界对象。

噪音对象：既不是核心对象也不是边界对象的其他数据对象［3］。

2 现有相关算法分析

2.1 基于SNN相似性的Jarvis-Patrick算法

基于SNN相似性算法的基本思想是：如果2个数据对象与其他许多相同的数据对象具有相似性，尽管直接的相似性度量方法可能确定不了这种相似性，但是这2个数据对象之间的相似性是成立的。SNN相似性定义为具有低密度或者密度变化较大特征的数据集合的聚类分析提供了可行的思路。JP（Jarvis-Patrick）算法通过最近共享邻居方法进行对象聚类，该算法的执行需要确定数据对象之间距离的度量方法以及2个参数J和K，J是最近邻居列表的大小，K是共享邻居的个数。该算法的描述如下：

1）对聚类分析的数据集合中的每一个对象确定它的J个最近的邻居。

2）把符合条件的对象分配到同一个簇中，它们相互包含在对方的最近邻居列表中，并且至少拥有K个共享的邻居对象。

因为JP聚类算法是基于SNN相似性概念的，所以它能够处理带有噪声、边界的数据集合的数据分析任务并且能够发现不同大小、形状和密度的数据对象簇；该算法对于高维数据的分析处理、特别是对于具有强关联性的结合紧密的簇的发现也是非常有效的。然而，JP算法把簇定义为在SNN相似图中相连接的对象集合，通过对单连结的判定来决定是否对一个对象集合进行分割或保留为一个簇，因此JP聚类算法在一定意义上是脆弱的，它可能分割真正的簇或者合并应该保持分离的簇。另外，JP算法不能实现对象的完全聚类，最佳参数的选择也较困难［2－3，5］。

2.2 基于SNN密度的聚类算法分析

因为SNN相似性反映了数据对象在数据空间中的局部分布特征，它对数据空间中密度和维度的变化具有相对较好的适应性，因此选择它作为新的密度度量的方法是非常有意义的。SNN密度方法通过数据对象周围的相似对象的个数来确定数据空间的密度，则一个局部对象空间的密度的高低可以通过它的SNN密度来反映，这样的方法对于具有较大范围密度变化的数据空间具有较好的适应性，并且对低密度的簇仍然具有较好的反应能力。将SNN密度方法和DBSCAN（density-based spatial clustering of application with noise）结合可以生成新的聚类算法，新算法跟JP算法一样以SNN相似图开始，通过阈值来完成SNN相似图的疏化并且把相连接的对象分配到相同的簇。基于SNN密度的算法描述如下：

a）计算数据空间的SNN相似图；

b）根据用户选定的Eps和MinPts参数应用DBSCAN算法进行聚类运算。

该算法可以自动的确定数据集合中簇的个数，在聚类过程中会抛弃掉噪音、边界以及非强连接的数据对象，适合于处理与文档相关的聚类问题，比如WEB数据挖掘问题等。SNN密度和核心对象的定义增强了算法的适应能力和灵活性。该算法的局限性与JP算法类似，另外让用户选定合适的Eps以及MinPts参数是较困难的［2－3］。

3 基于局部集聚特征的聚类算法

SNN相似性度量方法以及SNN密度度量方法，都是基于数据空间中对象的局部分布特性来考虑的，主要考虑算法对数据空间中簇的密度、形状等问题的适应能力。而基于局部集聚特征的聚类算法主要关注于数据空间中数据对象的局部集聚特征的分析和应用，分析数据对象周围的共享邻居的形状、大小、密度等局部集聚特征，并以此重新定义数据对象的相似性和密度等度量方法，进而提高算法的适应能力和优化的效率。数据对象之间的共享邻居本身就是一个局部的数据对象簇，相对于周围其他的数据对象而言具有较强的集聚特性，研究它的数据分布特征，对于确定数据对象的相似性和密度是非常有意义的工作。

3.1 基于局部集聚特性的相似性分析

由于JP算法采用输入参数k作为数据对象相似性计算的阈值条件，对于具有较强集聚特性的局部小的数据集合的发现是不利的，如图1a）所示，当参数k设定为6时，尽管它们之间局部分布是较为疏远的，数据对象A和B将被分配到同一簇中。另外基于SNN密度的算法采用输入参数Eps作为限定参数去度量数据对象的相似性，所以数据集合局部配置的形状大小等特性的考虑对于发现具有较强集聚特性的局部簇也是非常有用的，如图1b）所示，对象A和B在局部配置上是较为松散的，但是却在Eps的限定范围内，而数据对象C相较于对象A而言与对象B具有更强的连接性，尽管这种连接不是直接的。

为了更好的利用数据分布的局部特性实现对数据对象相似性度量，被SNN评估的两个对象之间的相似性可以通过以下几个方面来体现，比如被评估对象之间的局部共享邻居是否拥有相对较高的密度、相对于共享邻居的分布形状来说是否具有相对较近距离等，如果上述指标达到了用户预期，则可以认为在局部范围内被评估对象之间具有较高的相似性。

图1 数据对象局部分布特性Fig.1 Local characteristics of data object

3.2 局部集聚特征定义和度量方法

局部共享邻居中所有的数据对象相对于其他数据对象而言可以看作一个具有较强集聚特性的完整的簇。因此可以把它的局部集聚特性作为衡量2个具有相同共享邻居的数据对象是否具有较高相似性的依据。简单的来考虑，在局部数据区域，如果2个数据对象具有相对近的距离，则可以认为它们具有较高的相似性。因为数据对象的分布可能存在较大的变化，为了动态确定什么是相对于局部区域比较近的距离，需要对局部数据的分布特性进行分析，如局部簇分布形状、大小和密度等特征。共享邻居簇的大小作为参数由用户根据分析处理的数据类型设定，因此局部数据集聚特征可以简化为局部形状和局部密度的表示，其中密度可以由所有共享邻居簇的成员的平均距离LAD（local average distance）来衡量。由于局部数据分布的任意性，其分布形状的度量方法可以简化为2个主要的方面，局部最大距离LMD（local maximum distance）和局部径向距离LRD（local radial distance）（如图2所示）。局部数据特征的定义如下：

其中：CSNN是共享邻居的集合；n是CSNN中数据对象的个数；Line X定义为穿过具有最大距离的2个对象点的直线。

3.3 基于局部集聚特征的聚类算法

通过对不同基于密度的聚类算法的分析研究，为了更好地适应不同类型的数据对象集合，结合对数据对象局部集聚特征的定义，在JP算法和基于SNN密度算法的基础上，提出了新的聚类算法，即基于局部集聚特征的聚类分析算法，该算法在主要步骤上与JP算法相似，但是把数据集合的局部分布特性作为参考，使用LMD和LAD作为动态阈值去控制SNN相似性的计算。基于局部集聚特性的聚类算法的实现步骤描述如下。

第1步：通过LAD阈值的控制计算数据对象的相似矩阵。对于每一对数据对象，扫描数据集合建立它们的共享邻居集合，则可以把共享邻居的K个对象看作是一个具有较强集聚特性的局

部簇，然后计算K个数据对象的平均距离作为局部的动态阈值去控制相似图的生成。

第2步：应用相似性阈值去发现相互连接的对象集合，并同时动态的调整簇的成员对象的隶属关系。应用相似性阈值疏化簇连接关系图能够简化相似性计算和改进算法发现簇的效率。在完成簇的疏化工作后，需要相应的方法去发现和展示对象连接关系图中存在的簇，连接对象集合的发现方法的描述性伪代码如下：

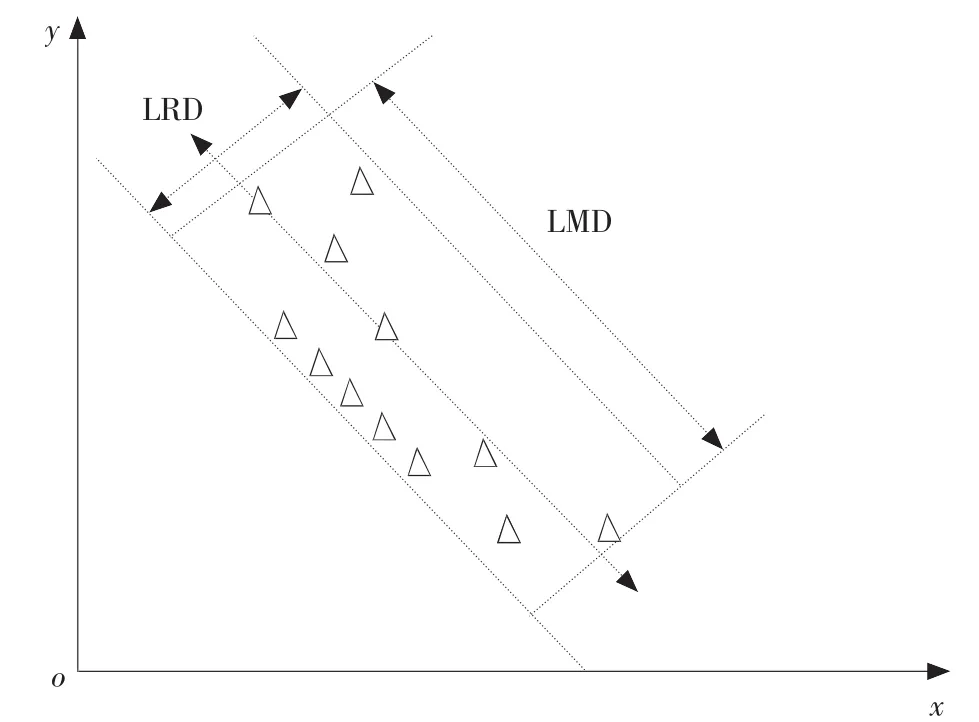
图2 共享邻居簇局部特征分析图Fig.2 Map of local characteristics analysis

3.4 算法的实验结果与评估

在聚类分析中，几乎所有的聚类算法都会在数据对象集合中发现簇，不管相关数据集合中的对象是否存在自然的簇结构，因此对聚类结果的评估是一项非常重要的工作。每一种聚类算法都会定义它自己的适合目标数据集合的发现簇的类型，所以对于不同的聚类分析算法需要定义相应合适的发现簇的评价的方法。基于距离的相似定义的优势是容易理解和计算，对于基础类聚类算法的研究评价，采用该类相似性定义是很好的选择，两个簇相似性定义方式可以有以下方式［6］：

本文设计的聚类算法由于采取了与JP方法以及SNN密度算法相似的数据处理步骤和数据存储结构，因此它的实现在时间和空间复杂度上与它们相同，不会额外增加系统开销。为了测试该算法的聚类效果以及准确性，采用随机分布和合成的数据对象集合作为测试数据集合，部分数据对象如表1所示。设定相同的初始条件，对同一组数据对象分别应用JP，SNN密度以及基于局部特征的聚类算法，其实验结果如表2所示，通过对不同聚类算法的在同一数据对象集合上的聚类结果进行比较，发现该算法在分析处理具有自然分布的数据对象集合时能够得到更好集聚的簇，因此改善了聚类的质量。

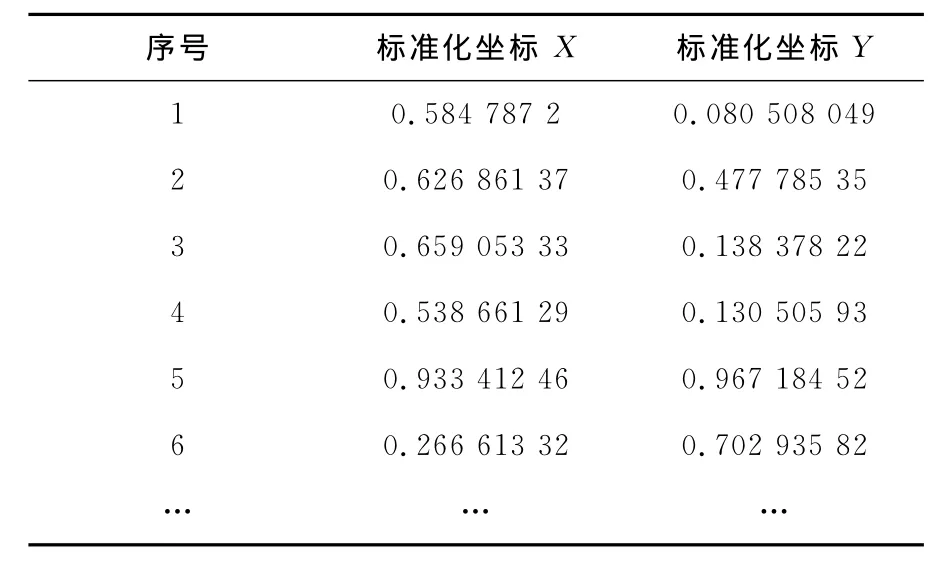
表1 部分实验数据Tab.1 Part of experimental data set

表2 实验结果Tab.2 Experimental result

4 结 论

在对相关领域已有的算法进行综合研究的基础上，为了能够更好地提取和表达数据对象的局部集聚特征，笔者对聚类分析中数据的局部集聚特征进行了详尽的分析和定义，分析了其应用依据，并提出了基于局部集聚特征的改进的聚类分析算法，该算法对于不同密度以及形状的目标数据集合均有很好的适应性。将该算法应用到随机分布和合成的数据对象集合上进行聚类分析，能够准确地发现自然分布的簇以及在局部有较强集聚特性的较小的簇。相较于其他相关算法而言，该算法的实现没有提高时间和空间复杂度，由于强化了数据对象局部分布特征的应用，进而改善了聚类的质量。

［1］ ALMEIDA J A S，BARBOSA L M S，PAIS A A C C，et al.Improving hierarchical cluster analysis：A new method with outlier detection and automatic clustering［J］.Chemometrics and Intelligent Laboratory Systems，2007，87：208-217.

［2］ HAN Jia-wei，KAMBER M.数据挖掘概念与技术［M］.第2版.北京：机械工业出版社，2007.251-299.

［3］ TAN Pang-ning，STEINBACH M，KUMAR V.数据挖掘导论［M］.北京：人民邮电出版社，2006.

［4］ TONNY J O.A new-fangled FES-k-means clustering algorithm for disease discovery and visual analytics［J］.Eurasip Journal on Bioinformatics and Systems Biology，2010（4）：1-14.

［5］ FERNANDO C，RICHARD W.A methodology for dynamic data mining based on fuzzy dustering［J］.Fuzzy sets and System，2005，150：267-284.

［6］ QIAN Wei-ning，ZHUO Ao-ying.Analyzing popular clustering algorithms from different viewpoints［J］.Journal of Software，2002，13（8）：1 382-1 394.

Research in clustering algorithm based on local agglomerative characteristics

NIU Xi-xian1，ZHAO Li-chuan2
（1.Faculty of Information Technology and Propagation，Hebei Youth Administrative Cadres College，Shijiazhuang Hebei 050031，China；2.Logistics Group，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

The SNN similarity and density based clustering，as one of the most important unsupervised clustering method，has been proved to produce good results in finding clusters of various sizes and shapes.But these algorithms still have some limitations.For example，Jarvis-Patrick scheme of finding clusters by single link，may separate real clusters or merge clusters which should be kept separated in certain situations，and the determination of Eps and MinPts，the parameters of SNN density method，is hard for users.To deal with these problems，the paper gives analysis and definition of local agglomerative characteristics presented in clustering procedure；then proposes a new clustering algorithm which use local gathering features to control clustering progress.The algorithm can work well in finding different size and density clusters，highlighting the local features of data analysis and improving the quality of data clusters.

data mining；clustering；local agglomerative characteristics；SNN density

TP301

A

1008-1542（2011）05-0466-05

2011-04-02；

2011-08-28；责任编辑:张 军

牛习现（1972-），男，河北赞皇人，讲师，硕士，主要从事数据挖掘、网络管理方面的研究。