基于邻域粗糙集和蚁群优化的属性约简算法

张冬雯，王 鹏，仇计清

（1.河北科技大学理学院，河北石家庄 050018；2.河北科技大学信息科学与工程学院，河北石家庄050018）

基于邻域粗糙集和蚁群优化的属性约简算法

张冬雯1，王 鹏2，仇计清1

（1.河北科技大学理学院，河北石家庄 050018；2.河北科技大学信息科学与工程学院，河北石家庄050018）

在分析单一、给定的邻域大小设定方法弊端的基础上，提出了基于属性数据标准差的阈值设定方法，并将蚁群优化算法引入到属性约简中，以属性重要度为启发信息，构造了基于邻域粗糙集和蚁群优化的属性约简算法，使用了4个UCI数据集进行约简。实验结果表明，提出的算法在约简的分类精度和约简中属性个数方面具有更好的性能。

邻域粗糙集；蚁群优化；属性约简；标准差

属性约简的目的是在不降低预测分类精度的前提下对数据的属性集合进行约简，摒弃冗余的属性，从而降低对数据处理时的时间和空间复杂度［1］。所有的属性约简算法都包括2个重要的部分：评价函数和子集生成器。评价函数是对属性子集的分辨能力的一种量度，它能够对属性子集的预测分类精度进行评估；子集生成器是使用评价函数对属性集合进行约简，得到最优属性子集的过程。作为一个重要的粒度计算工具，粗糙集理论（RST）［2］被广泛应用于属性约简的算法中［3－5］。然而，粗糙集理论使用等价关系和等价类的概念对整个论域进行划分，这只适用于处理离散型属性的数据。对于现实应用中的大量数据，往往同时存在离散型和连续型2种属性。对于连续型属性，应用粗糙集理论就必须首先对这些属性进行离散化，显然，对连续型属性进行离散化必然会带来数据信息的丢失。文献［6］提出了基于邻域的粗糙集（NRS）模型来对连续型属性进行约简的算法。该算法使用邻域关系对论域进行划分，然后使用这种由邻域关系形成的粒子族来对决策属性进行逼近，从而提出了邻域决策表模型，并基于此模型构造了连续型属性的属性约简算法。作为该模型的一个重要参数，邻域的大小对属性约简的结果有着重要的影响，但是在文献［6］中并没有对这一参数进行分析。在上面提到的属性约简的算法中，都使用了贪心算法作为属性约简的子集生成器。然而，由于贪心算法往往只能够找到较优的约简结果而不是最优的约简结果，所以，许多研究者采用了基于群的算法作为子集生成器来构造最优约简。例如：遗传算法（GA）［7］，粒子群优化算法（PSO）［8］和蚁群优化算法（ACO）［2，9-11］。

笔者对文献［6］中的方法进行改进，提出了一个基于邻域粗糙集模型和蚁群优化的属性约简算法。在本算法中，笔者使用基于属性数据分布特征的参数作为邻域的大小，并将基于邻域粗糙集的属性重要度作为蚁群算法的启发信息，使用蚁群算法作为子集生成器，得到属性的最优约简。

1 预备知识

1.1 邻域粗糙集

定义1 给定样本集合U＝｛x1，x2，…，xn｝，U 称为论域，C是条件属性集，D是决策属性集，如果C中所有属性能够产生论域U上的一簇邻域关系N，则称NDT＝〈U，C∪D，N〉为一邻域决策系统。

定义2 给定一邻域决策系统NDT＝〈U，C∪D，N〉，决策属性D将U划分为M 个等价类：X1，X2，…，XM，δB（xi）是由B⊆C对xi生成的邻域信息粒子，则决策属性D关于B的上下近似定义为

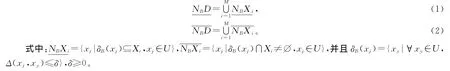
1.2 蚁群优化算法

蚁群优化算法是一种基于蚂蚁的社会行为模型的算法，它能够将复杂的组合优化问题简化为在图中寻找最短路径。它的主要思想是生产一定数量的蚂蚁，通过蚂蚁搜索路径建立可行解。先将蚂蚁随机放置在若干结点上，每只蚂蚁从初始结点出发，根据路径上的启发信息和信息素浓度以某种概率策略选择下一结点，直到建立可行解。每只蚂蚁根据解的优劣对路径上的信息素浓度进行更新。如此周而复始，直到最终找到最优解。

1）选择概率公式 1只蚂蚁从结点i选择结点j的概率为

定义3 给定一邻域决策系统NDT＝〈U，C∪D，N〉，条件属性子集B⊆C，则决策属性D关于B的依赖度定义为

式中：τij是在给定的边（i，j）上的信息素；α是控制信息素对概率影响的参数；ηij是结点j对结点i的启发信息；β是控制启发信息对概率影响的参数。

2）信息素更新公式 每条边上的信息素会因为蚂蚁的走过而增强，同时会随时间而蒸发，其更新的公式为

式中：τij是在给定的边（i，j）上的信息素；ρ是信息素蒸发的速率；Δτij是信息素增强值。

2 主要研究成果

2.1 邻域大小的设定

在邻域粗糙集中，邻域的大小是一个关键的参数，如何设定一个合适的阈值将直接影响属性约简的结果。邻域信息粒度是由邻域大小决定的，这个阈值过大时，对某一条件属性集合，几乎所有的样本会被划分到同一个邻域关系里，这时，决策属性对该属性的依赖度将变得非常小，从而使得约简后的属性变得太少。相反，这个阈值为0时，邻域粗糙集将会等价于经典的粗糙集理论。为了说明阈值的大小对决策属性依赖度的影响，现举例如下。

例1 在表1中，F1和F2是2个条件属性，首先设定邻域大小的阈值δ＝0.6，则可以通过式（3）计算出γF1（D）＝0。同理，设定δ＝0.04，可以得到γF1（D）＝1。可见，邻域大小的设定对属性的依赖度有着重要的影响。

例2 邻域大小对属性依赖度有一定的影响，图1显示了不同的阈值对属性依赖度的影响。笔者选用UCI数据集中的Wine数据集作为源数据，选取第8，9，10，11，12，13属性作为属性集合，阈值从0到0.5以0.1为步长分别计算该属性集合的依赖度。从图1中可以发现，当阈值为0时，属性集合的依赖度为1.0；而当阈值接近0.5时，依赖度变为0。而且，随着阈值的变大，依赖度逐渐变小。

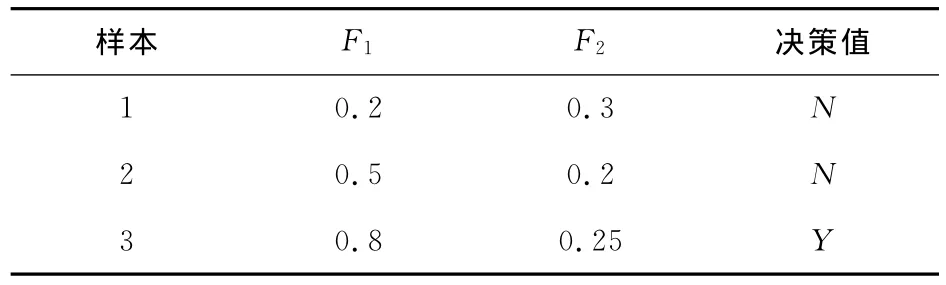
表1 阈值分析实例Tab.1 An example of threshold analysis

由以上2例可以看出，阈值的设置对属性约简有重要的影响，如果为邻域设定一个特定的值，往往不能够得到正确的属性约简。而且每一属性的值，即使将它们都规范化到［0，1］，其数据的分布特征也是不相同的，以例1中的数据为例，通过对属性F1和F2中数据的标准差进行计算可以发现，F1的标准差SDF1远大于F2的标准差SDF2，所以，当为属性F1和F2设置相同的阈值时，必然会为属性约简带来更大的误差。

为了减小这些误差，笔者一方面采用一个阈值集合取代单一的阈值来设置邻域的大小，这些阈值对应于每一个属性；另一方面采用基于属性值的分布特征的参数作为阈值。作为一个统计量，标准差显示了数据在平均值的平均波动大小。当标准差小时，所有的数据都接近于平均值，这时需要为邻域设定一个较小的阈值；相反，当标准差较大时，这个阈值也要变大。正是由于阈值与标准差之间的线性关系，笔者选择SD／n作为邻域大小的阈值，这里n是控制这种线性关系的参数，可以针对不同的数据在实验中进行设置。

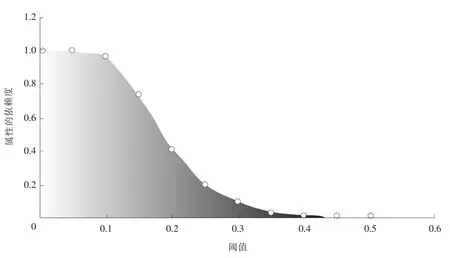
图1 邻域大小对属性依赖度的影响Fig.1 Influence of neighborhood on feature dependability

定义6 给定一邻域决策系统NDT＝〈U，C∪D，N〉，SD＝｛SD1，SD2，…，SDm｝是包含每个属性的数据的标准差的集合，m是属性的个数，s是U中的样本总个数，对属性i（1≤i≤m）在U上的邻域关系Ni的关系矩阵为

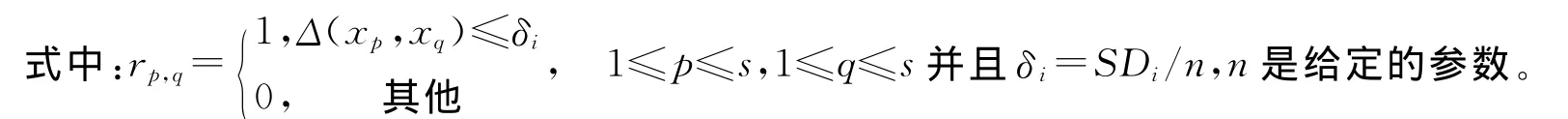
2.2 基于NRS和ACO的属性约简算法

属性约简的目的是在保持较高分类精度的前提下，找出初始属性集合的最小属性子集。笔者采用ACO算法作为属性约简算法的子集生成器。首先，将属性约简问题转化成1个可以使用ACO算法的模型。如图2所示，1个结点代表了1个属性，连接2个结点的边代表从一属性对下一属性的选择。蚂蚁在图2中对所有节点进行递增的移动，当满足终止条件时停止移动，就得到一条路径，这样属性约简的问题就转化为在图2中找出最短路径的问题。

1）基于ACO的属性约简算法的启发信息

在以往的研究中，很多的量度方法被作为启发信息应用到ACO算法中，如基于信息熵的方法［11］、基于粗糙集的方法［2］。笔者使用基于邻域粗糙集的量度方法作为ACO算法的启发信息。

定义7 给定一只蚂蚁走过的属性的集合B，p为蚂蚁当前所在的属性结点，r为蚂蚁可能选择的下一属性结点，则r对p的启发信息定义为

其中SIG是在定义5中给出的属性重要度函数。

2）基于ACO的属性约简算法的信息素更新

在每只蚂蚁构建出一个解后，在每条边上的信息素将按式（6）进行更新，每一条边都会进行信息素的挥发，而只有构建出较优解时，蚂蚁才会在这个较优解中的各属性结点之间的边上对信息素进行加强。在时间t，信息素加强的数量为

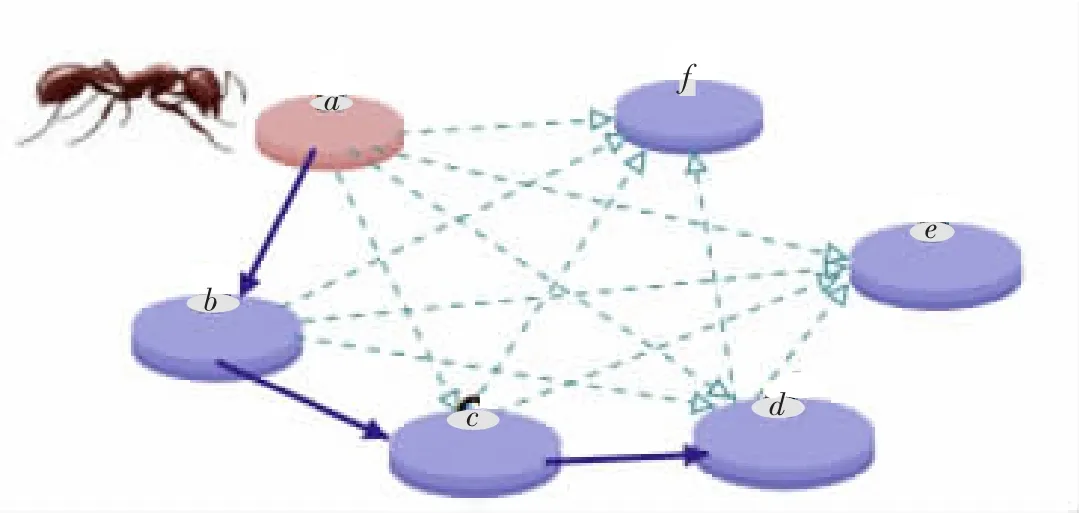
图2 属性约简转化成ACO问题的模型Fig.2 Model of feature selection reformulated as ACO

式中：q为一个给定的参数；R（t）为在时间t的最优解。

3）基于ACO的属性约简算法的终止条件

每只蚂蚁独立进行解的生成，当达到终止条件时，解的生成过程将结束。终止条件有2个：1）根据定义3判断当前构筑的解是否为所有属性的一个约简；2）当前的解中属性的个数是否小于临时最优解。

第1个条件表明蚂蚁找到了1个新的约简，第2个条件将新得到的约简与临时最优解进行比较，如果当前的约简优于临时解，则用当前约简替换临时解。

在时间t达到最大值时，整个算法将结束，然后输出最终的解。算法的主要步骤如下。

Step1 初始化

1）Rmin＝C，C为条件属性集合；

2）设置Tτ，Tτ为每个条件属性的信息素数量的集合；

3）定义最大的时间和蚂蚁个数；

4）定义参数α，β，p，q的大小。

Step2 计算每1个条件属性的邻域关系

对C中每个属性，通过式（7）计算其领域关系矩阵。

Step3 解的生成

1）每只蚂蚁都随机选择第1个属性，然后独立进行解的生成；

2）通过式（5）和式（8）计算出每个待选属性的选择概率，蚂蚁选择概率最大的属性作为下一属性；

3）当达到终止条件1）时，生成解的过程将结束；

4）构筑的解即为C的一个约简。

Step4 更新Rmin

当达到终止条件2）时，即当前的约简中属性的个数小于Rmin中属性的个数，则将当前的约简赋值给Rmin，否则继续。

Step5 更新信息素

1）当Rmin发生更新时，在Rmin中每个属性的信息素通过式（6）进行加强；

2）对每个时间t，每个属性的信息素都通过式（9）进行蒸发。

Step6 判断终止条件

当迭代次数达到最大迭代数时，算法将结束，并输出Rmin，否则继续。

Step7 转到Step3，然后继续。

3 实验和结果

为了验证笔者提出的算法性能，使用4个UCI数据集进行实验，并与文献［7］中提供的算法（FSNMA）进行比较，使用C4.5和Navie Bayes（NB）机器学习的算法，评估和FSNMA算法在约简检测精度上的差异。所有的实验是在3.0 GHz CPU，1 GB内存的计算机上完成的，使用Matlab实现。

3.1 数据集

从UCI数据集中选取4个数据集作为实验的数据，即Ionosphere数据集、Sonar数据集、S-soybean数据集和Wine数据集。表2详细给出了4个数据集的样本个数、属性个数以及各自的类别种类。

3.2 参数设置

在笔者提供的方法中，用于子集生成器的参数进行如下的设置：α＝1，β＝0.1，ρ＝0.2，q＝1，蚂蚁的个数为条件属性的个数，最大迭代数为50。参数n是控制邻域大小的关键参数，为了得到最佳的参数设置，以0.1为步长，从2到3为n进行赋值，以评估不同的参数值对分类精度的影响，从而确定最佳的参数值。以Ionosphere数据集为例，图3显示了参数n的不同取值对分类精度的影响。

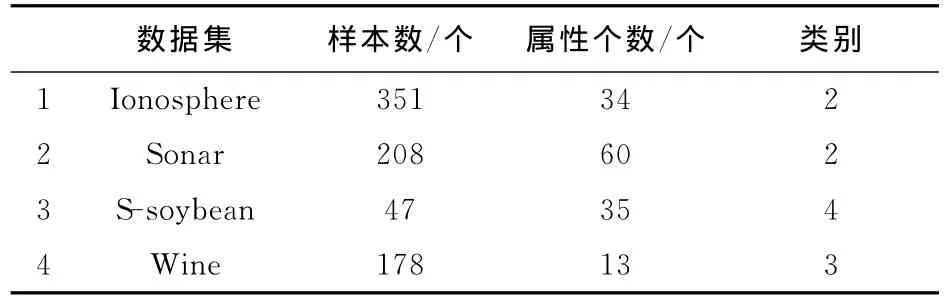
表2 4个UCI数据集Tab.2 Detail of the four UCI datasets

从图3中可发现，当n的取值为2.8时，C4.5算法和NB算法都能达到较高准确性，虽然当n为2.2时C4.5算法拥有最高的准确性，但此时NB算法的准确性却很低，所以，弃用n＝2.2。同理，n＝2.6也不会被选择。用以上的评估方法，分别为Sonar，S-soybean，Wine数据集设置参数n为2.2，2.0，2.0。

3.3 实验结果

表3显示了使用该算法和FSNMA算法得到的约简中的属性个数。从表3可以看出，2种属性约简算法都能有效降低数据的属性个数。FSNMA算法将属性的平均个数从35.5个约简到7.25个，而本文算法能够约简到5.75个。具体到4个数据集，在Sonar，S-soybean，Wine数据集2种算法的约简在属性个数上相同，但具体属性不同，而在Ionosphere数据集上本文算法得到约简中的属性个数明显比FSNMA算法少。从表3结果可以看出，本文算法在约简的属性个数上具有一定优势。表4中给出了本文算法所得到约简的具体属性。

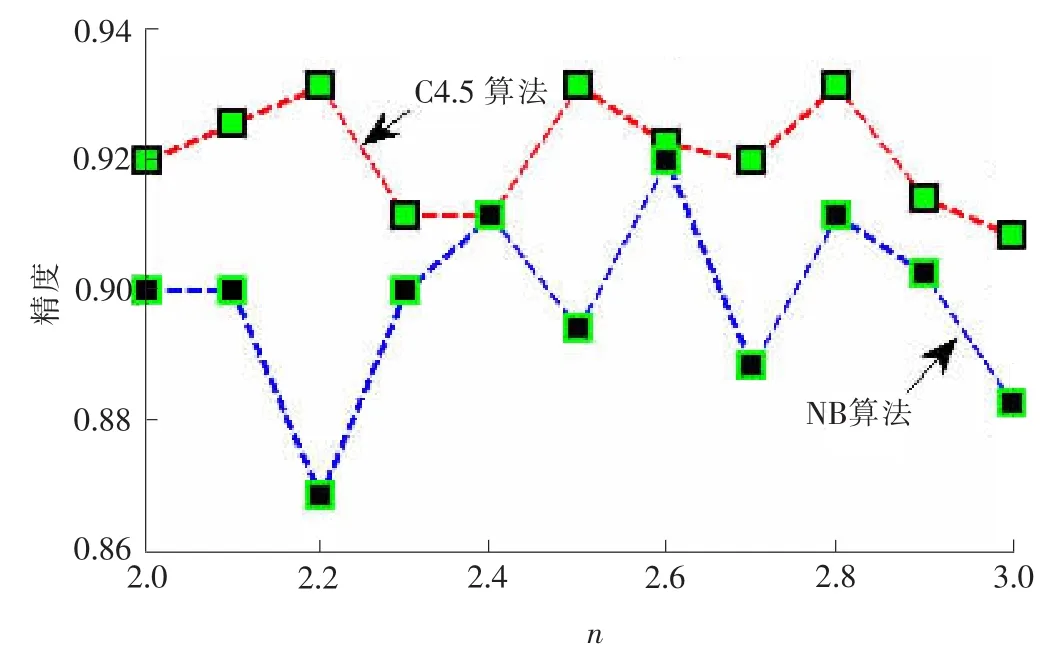
图3 参数n对分类精度的影响Fig.3 Influence of n on classification accuracy

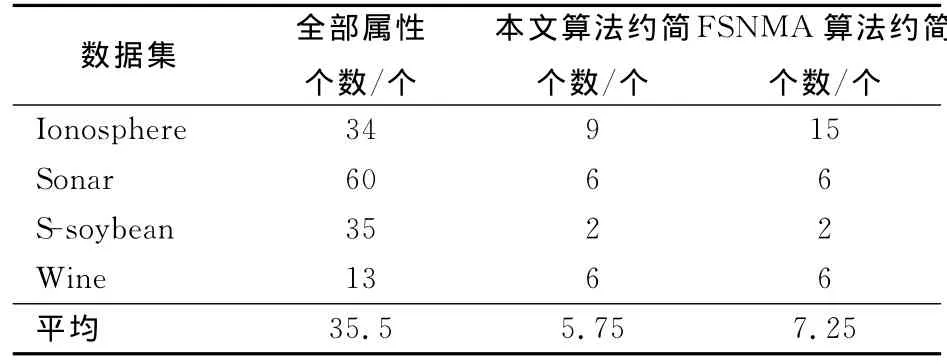
表3 属性约简中属性的个数Tab.3 Number of features selected

表4 4个数据集的属性约简Tab.4 Feature selection of the four datasets

为了评估本文算法在分类精度上的性能，笔者采用C4.5和NB分类算法对全部属性、本文算法和FSNMA算法的约简结果进行分类精度的计算，并将结果汇总到表5中。

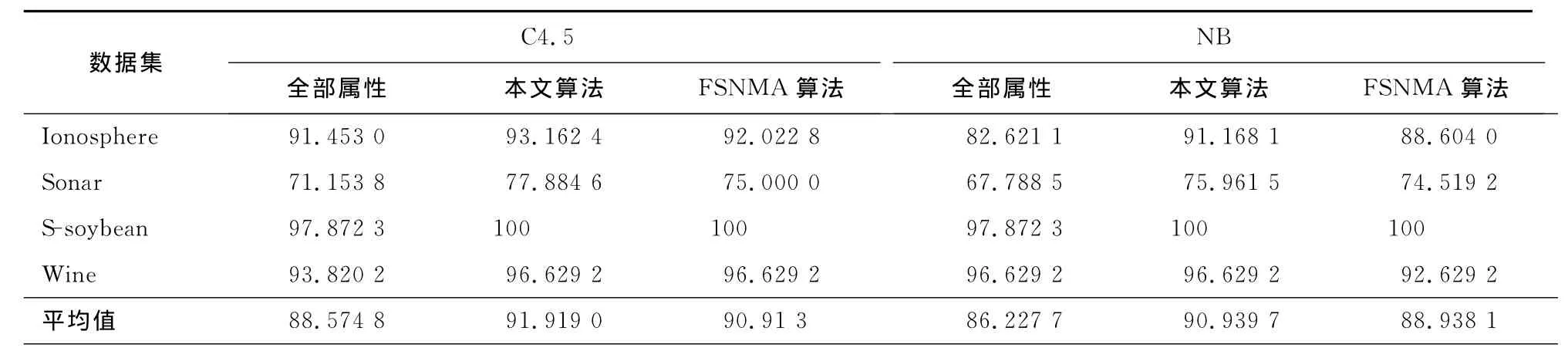
表5 分类精度Tab.5 Classification accuracy

从表5中可以看出，2种约简算法得到的约简在分类精度上都要优于全部属性，同时由于属性个数的降低，从而减少了分类算法进行分类精度计算时的时间。特别是对S-soybean数据集，约简后的分类精度能够达到100%。对比本文算法和FSNMA算法，除在S-soybean数据集上两者都达到100%的分类精度外，本文算法都表现了更好的分类精度。

综合表3、表5可以看出，相比于全部属性，本文算法能够有效找到属性约简，而且约简的分类精度更高。相比于FSNMA算法，本文算法得到的约简不仅属性个数更小，同时在分类精度上具有更好的性能。

4 结 语

提出了一种基于邻域粗糙集和蚁群优化的属性约简算法。在仔细分析了邻域大小的阈值对属性依赖度的影响后，提出了依赖于属性数据本身标准差的参数作为邻域大小的阈值。通过使用C4.5和NB算法对属性约简的结果进行分类精度比较，实验结果表明本文算法能够得到较好的性能。

［1］ RICHARD J，QIANG S.Computational and Feature Selection：Rough and Fuzzy Approaches［M］.Hoboken：Whiey-IEEE Press，2008.

［2］ 苗奇谦，李道国.粗糙集理论、算法与应用［M］.北京：清华大学出版社，2008.

［3］ SWINIARSKI R W，SKOWRON A.Rough set methods in feature selection and recognition［J］.Pattern Recognition Letters，2003，24（6）：833-849.

［4］ ZHAI Lian-yi，KHOO L P.Feature extraction using rough set theory and genetic algorithms-an application for the simplification of product quality evaluation［J］.Computers ＆Industrial Engineering，2002，43（4）：661-676.

［5］ ZHONG N，DONG J.Using rough sets with heuristics for feature selection［J］.Journal of Intelligent Information Systems，2004，16（3）：199-214.

［6］ 胡清华，于达仁.基于邻域粒化和粗糙逼近的数值属性约简［J］.软件学报（Journal of Software），2008，19（3）：640-649.

［7］ 蒙祖强，黄柏雄.不一致不完备决策系统中属性约简的比较研究［J］.控制与决策（Contrd and Decision），2011，26（6）：867-872.

［8］ 胡 峰，王国胤.属性序下的快速约简算法［J］.计算机学报（Chinese Journal of Computers），2007，30（8）：1 429-1 435.

［9］ KE L L，FENG Z R.An efficient ant colony optimization approach to attribute reduction in rough set theory［J］.Pattern Recognition Letters，2008，29（9）：1 351-1 357.

［10］ CHEN Y M，MIAO D Q.A rough set approach to feature selection based on ant colony optimization［J］.Pattern Recognition Letters，2010，31（3）：226-233.

［11］ DORIGO M.Ant Colony Optimization［M］.Cambridge：MIT Press，2004.

Approach to feature selection based on neighborhood rough set and ant colony optimization

ZHANG Dong-wen1，WANG Peng2，QIU Ji-qing1
（1.College of Sciences，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China；2.College of Information Science and Engineering，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

This paper analyses the weakness of setting a single，specified threshold for the size of neighborhood，and then puts forward a new neighborhood setting method based on the standard deviation of feature data.The paper introduces ant colong opbimization（ACO）into feature selection and proposes an approved feature selection algorithm based on NRS and ACO，in which the feature importance is taken as the heuristic information.In order to evaluate the performance of the proposed algorithm，four datasets from UCI are used and the experimental results show that the proposed algorithm has a better performance in classification accuracy of reduct and feature number in reduct.

neighborhood rough set；ant colony optimization；feature selection；standard deviation

O231

A

1008-1542（2011）05-0403-06

2010-12-26；

2011-06-08；责任编辑:张 军

国家自然科学基金资助项目（60874003）

张冬雯（1964-），女，河北石家庄人，教授，博士，主要从事优化、预测控制方面的研究。