四电极外流式电磁流量计仿真与实验研究
张广玉,刘宝龙,李隆球
(哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)
四电极外流式电磁流量计仿真与实验研究
张广玉,刘宝龙,李隆球
(哈尔滨工业大学机电工程学院,黑龙江哈尔滨 150001)
四电极外流式电磁流量计是一种新型的测量注入剖面流量的测井理想仪器,广泛应用于油田注水井、注聚井的流量测量。目前四电极外流式电磁流量计的研究主要在实际环境中开展,实验效率低、成本高。建立了四电极外流式电磁流量计的准确的有限元模型,将强耦合的方法应用在电磁-结构-流体耦合上,并在不同流速下开展了模型的响应及误差分析。研究表明,该有限元模型在一定程度上可用于电磁流量计的流场仿真分析。流速较小时,有限元仿真结果与实验误差较大;流速较大时,流场趋近于匀速场,仿真结果与实验结果误差较小。
电磁流量计;有限元;强耦合;多物理场
在油田三次采油中,注聚合物驱油是提高原油采收率的重要手段之一[1],它比水驱效果提高了20%左右;现场实验表明,过去常用的注入剖面测井仪器已经不适合注聚合物测井的剖面测试的要求。电磁流量计是一种新型的测量注入剖面的仪器,较好地解决了聚合物注入剖面的测井问题[2]。
四电极外流式电磁流量计是针对油田应用开发的一种特殊电磁流量计,其不仅具有普通工业电磁流量计无节流阻流,不易堵塞,耐腐蚀性好,测量精度不受被测介质温度、黏度、密度、压力等物理参数的影响且其示值在一定的电导率范围内与被标定的液体种类无关等特点,还具有体积小、耐高温高压、流场不对称对测量精度影响较小的优点,可以作为独立设备进行井下测量,也可以作为复杂智能测调系统的数据采集终端。其基本原理是基于法拉第电磁感应定律,即当导电液体流过磁场作切割磁力线运动时,则在垂直于流速向量和磁场向量的方向上会产生一个与流量大小成正比的感应电动势,其表达式为

式中:εab为感应电动势;a为电极1的位置坐标;b为电极2的位置坐标;B为流体微元处的磁场强度;V为流体微元的速度;d l为流体微元的长度。
因此可知,通过测得感应电动势的大小,即可测得流量大小。
目前,在电磁流量计方面的有限元建模研究较少。1996年,MICHALSKI等基于有限元建立的不同形状和尺寸的流体管道数值模型对励磁线圈的横截面形状进行寻优,以获得均匀的矢量积[3];2002年,MICHALSKI等用有限元方法建立了电磁流量计励磁线圈的3D混合数学模型[4];2009年,金宁德等用Ansys对四电极外流式电磁流量计建立了二维有限元模型,得出了数值模拟结果,提出了四电极外流式电磁流量计的理论分析方法[5](但这个模型无法进行仿真实验);邬惠峰等建立了普通工业内流式电磁流量计的二维仿真模型[6](内流式和外流式因其应用的场合不同,整个流量计的结构也不同);2010年,张志刚利用Matlab对四电极外流式电磁流量计权重函数分布情况进行了理论推导和仿真计算,为进一步开展四电极外流式电磁流量计的研究和开发设计奠定了理论基础[7]。大量研究表明,有限元方法是一种研究电磁流量计的有效手段。由于四电极外流式电磁流量计系统本身受结构参数和电气参数等众多参数的影响,影响规律复杂,改变某一个参数就需要变换硬件,实验效率低而且成本高。因此采用有限元方法建立能反映其特性的多物理场仿真模型,开展电磁流量计励磁规律和三维尺度下磁场分布规律及影响因素研究,可优化磁场设计参数,指导传感器的实验与设计,显著降低成本,提高开发准确率及效率。
1 流量计场路耦合有限元模型的建立
1.1 三维实体模型的建立与简化
电磁流量计实体模型中不仅包括线圈、线圈架、电极、测量管、绝缘套、空气域、流场域等主要部件,还包括平衡柱体、平衡柱套、电缆插头、过线塞座、过线塞套等辅助零件。由于辅件对磁场和电极的感应电动势没有影响,同时各个主要部件上都加工有装配特征,且这些特征都对磁场和信号也没有影响,因此为了提高计算效率,可对传感器模
型进行简化。简化后的模型包括:1)线圈,如图1a);2)线圈架,如图1b);3)电极,如图1c);4)空气域,如图1d);5)流体域,如图1e);6)测量管域,如图1f)。
笔者在Solidworks中建立了简化的传感器实体模型,然后将其导入强大的网格划分软件Hyper Mesh中进行布尔运算和网格划分,由于实体模型导入后会丢失体信息,因此模型导入后要重新利用各个实体的面重新生成体。
1.2 有限元模型的前处理及设置
Ansys在工程领域强大的求解能力众所周知[8],故采用Ansys软件作为电磁场求解软件。由于整个有限元模型中的各个部件都是三维实体,模型尺寸颇大,在进行网格划分时会有大量网格产生,增大计算量,而该模型中除了流体域和电极是计算域外,其他部分都不需要参与计算,因此将线圈、线圈架、电极的网格大小设置为2 mm,空气域的网格大小设置为3 mm,流体域的网格大小设置为1 mm。
有限元网格的质量直接影响计算精度,采用自动网格划分,单元形状为四面体,粗网格和细网格之间过渡并不光滑,因此将流体域和空气域之间的测量管域的网格单元大小设置为2 mm。网格划分后,导入Ansys中进行单元类型、材料、实常数、载荷、边界条件和场路耦合单元设置。线圈用铜线实现,匝数共6 500匝,其截面积为2.72×10-4mm2,体积为1.49×10-5mm3;线圈坐标系单独定义为局部柱坐标系,轴向为正Y方向,其余部件的坐标系使用全局笛卡尔坐标系,轴向为正Y方向。各个部件的材料参数设置见表1。
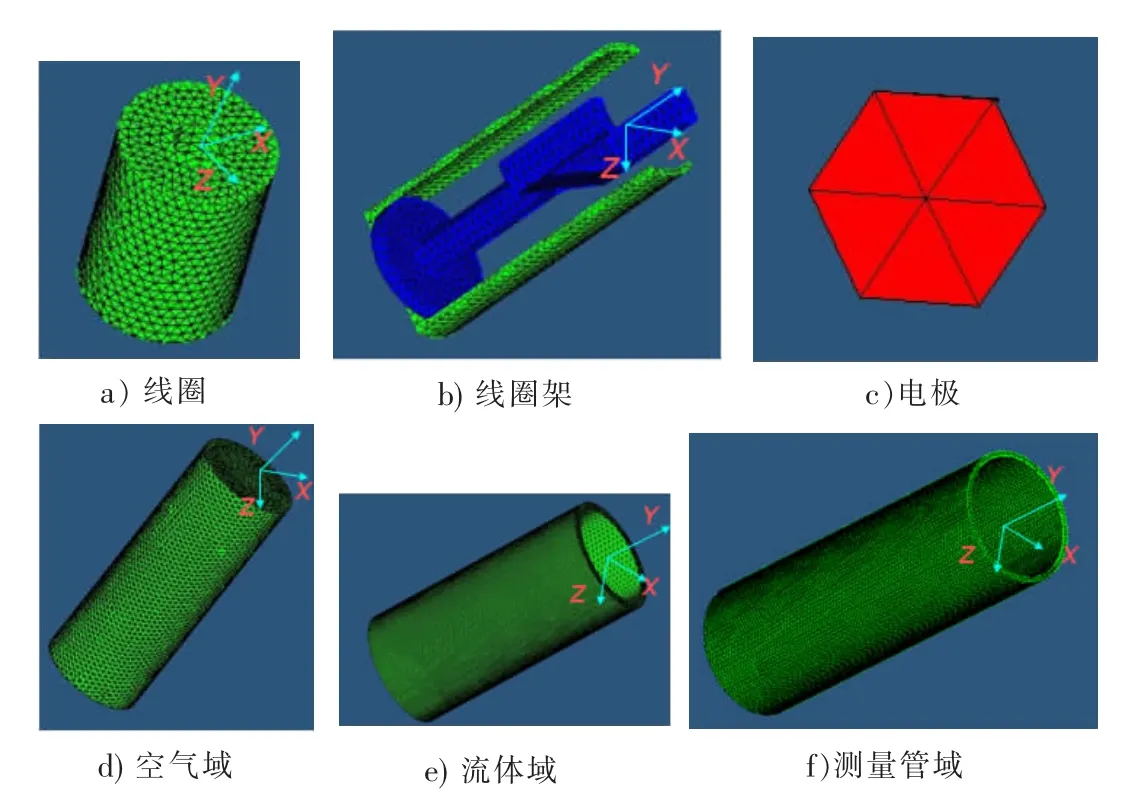
图1 四电极外流式电磁流量计有限元模型Fig.1 Finite element model of four electrodes outflow electromagnetic flowmeter
为了实现励磁方式的可编程,需要把线圈单元耦合到电路,因此建立2个Circu124分别实现独立电压源单元和耦合单元,Vj节点的电位定义为0,然后将线圈单元的任意一个节点定义为耦合单元的K节点以实现耦合,具体如图2所示。
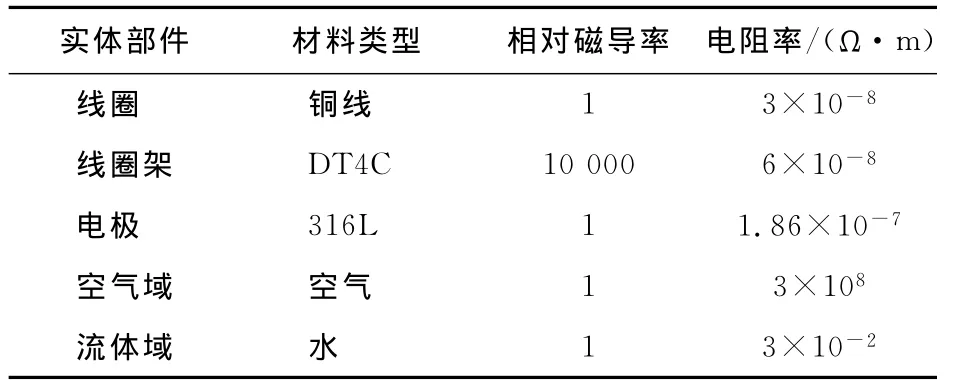
表1 各个部件材料参数Tab.1 Material parameters of the various components
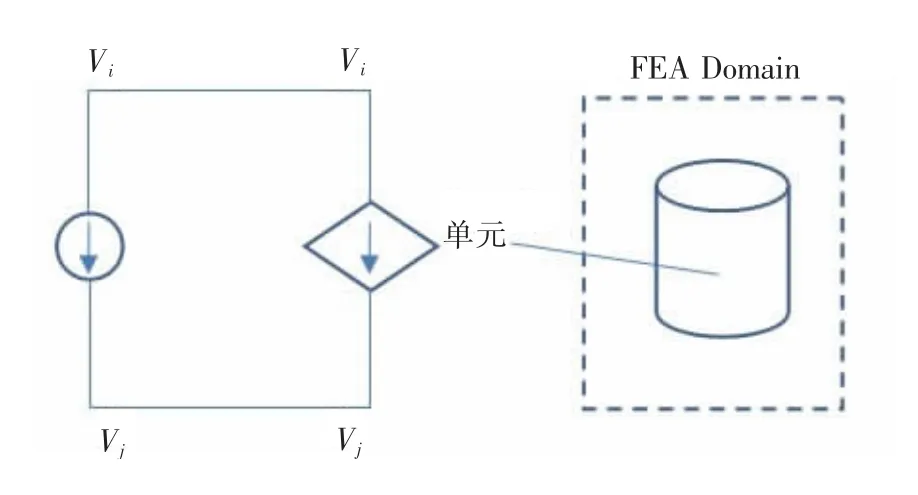
图2 场路耦合电路图Fig.2 Field-circuit coupling circuit
2 模型校验
为了保证模型的准确性,对建立的四电极外流式电磁流量传感器的三维有限元模型,从2个方面进行了校验:首先,给有限元模型施加恒值电流激励,选用静态求解类型,将模型最外圈节点的Ax,Ay,Az自由度均设为0,选择所有单元后进行求解,然后在后处理器中读入结果,画出电极附近的磁场分布,如图3所示,磁场分布符合金宁德等数值分析的结果[5],如图4所示;其次,在现有模型基础上加密网格单元,所得感应电动势大小前后误差小于5%,从而保证有限元计算结果不受网格质量变化的影响。综上所述,该有限元模型是准确的,可用来进行仿真研究。
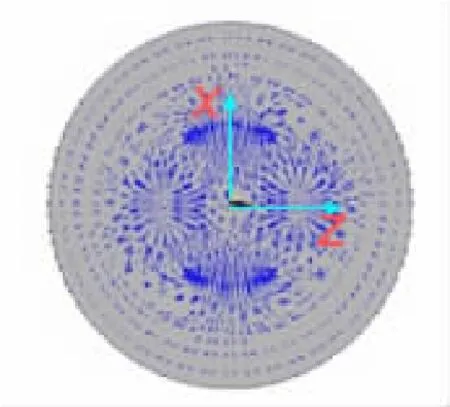
图3 电极附近磁场分布Fig.3 Magnetic field distribution around the electrodes
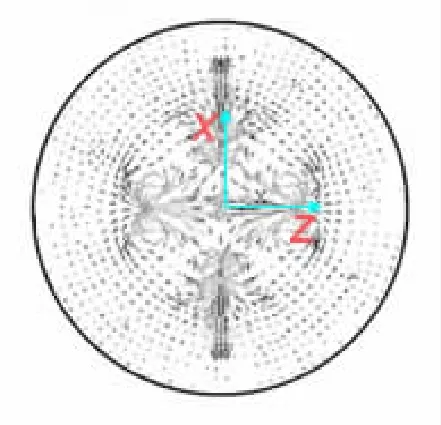
图4 二维模型电极附近磁场分布 Fig.4 Two-dimensional model of the magnetic field distribution around the electrodes
3 不同流速下模型的响应及误差分析
耦合分析分2种方法:强耦合(或称紧耦合)和弱耦合(或称松耦合)。强耦合通过单元矩阵或荷载向量把耦合作用构造到控制方程中,然后对控制方程直接求解,其缺点是在构造控制方程过程中常常不得不对问题进行某些简化,有时候计算准确程度较难保证。弱耦合是在每一步内分别对每一种场方程进行一次求解,通过把第1个物理场的结果作为外荷载加于第2个物理场来实现2个场的耦合。其优点是可以利用现有的通用流场和电磁场软件,并且可以分别对每一个软件单独地制定合适的求解方法;缺点是计算过程比较复杂。强耦合通常适合于对耦合场的理论分析,弱耦合适用于对耦合场的数值计算[9]。
仿真对象的外径尺寸是38 mm,其工作的管道内径为46 mm,根据截面积相等的原则,其等效管径为26 mm。当雷诺数Re<2 000时,管道内流动状态为层流;当4 000>Re>2 000时,管道内流动状态不确定;当Re>4 000时,管道内流动状态为湍流。当流动状态为湍流时,由可计算出紊流流动对应的最小平均流速V=0.092 m/s。
式中:V 为平均流速;D 为圆管直径,取26 mm;υ为运动黏度,取0.6×10-6m2/s。
因此,当管道内平均流速V>0.092 m/s时,管道内的流动状态为紊流;事实上,四电极外流式电磁流量计在工作的时候,管道内大多数的流动速度都大于这个值。当管道内的流动状态为紊流时,用CFD软件进行流场分析、计算,通过CFD模拟,可以分析并且显示流体流动过程中发生的现象,及时预测流体在模拟区域的流动性能[10],用有限元软件Ansys中的FLOTRAN CFD模块对其流场进行仿真分析,计算结果如图5所示。
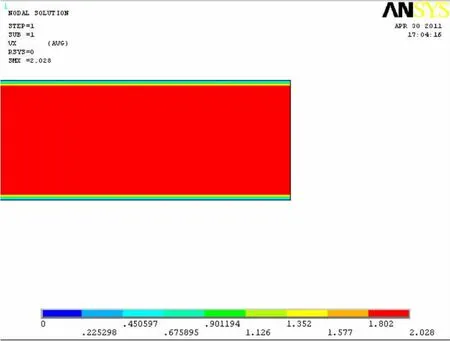
图5 实际管道在平均流速为2 m/s时的流场分布Fig.5 Flow field distribution of the average flow rate at 2 m/s
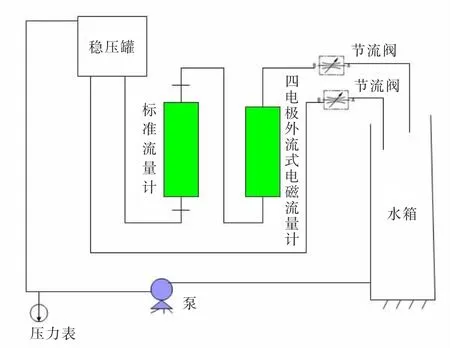
图6 电磁流量计实验台原理图Fig.6 Schematic of electromagnetic flowmeter bench
在近壁0.2 mm处速度较小,其余位置都接近平均速度。基于此,可以将流体等效为一个匀速导体,用强耦合的方法进行电磁-流场耦合的分析。
笔者在紊流场共选定了10个不同的流量值,独立电压源编程为两值矩形波,幅值为15 V,频率为1 Hz,对流量数据进行了仿真计算,并在实验台上得出了实验数据,实验台采用精度为0.5%的电磁流量计读取流量值,用信号处理电路采集四电极外流式电磁流量计的感应电动势信号,通过串口输入到计算机显示,实验台原理图如图6所示,最后对这2种数据进行了误差分析,结果见表2。
从实验结果和仿真结果的误差来看,流速较小的时候误差非常大,随着流速的加快,误差逐渐减小。这是因为流速越大,流场就越趋近于匀速场,仿真计算的方法越接近真实情况。误差一方面是由仿真模型的简化引起的,另一方面是由信号处理电路引起的,仿真模型反映了实际的情况,可以用于励磁技术实验等的理论分析。
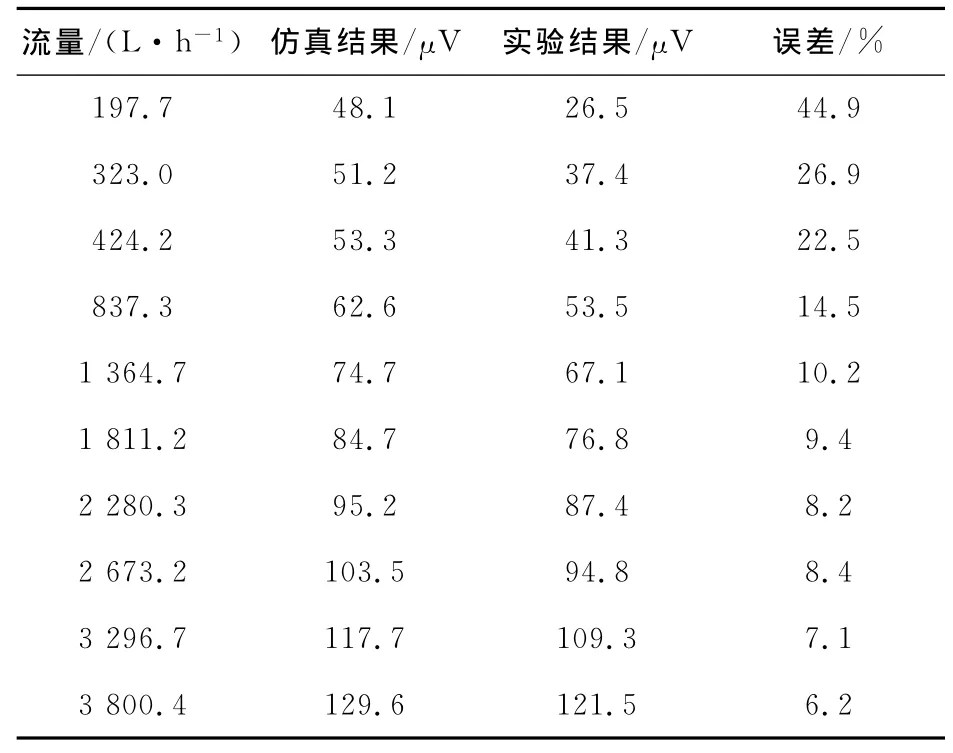
表2 仿真数据与实验数据对比Tab.2 Comparison between the simulation data and the test data
4 结 语
通过有限元方法建立了四电极电磁流量计的仿真模型,从2个方面对模型进行了校验,验证了模型的准确性。在不同平均流速下,用强耦合的方法仿真计算了模型的响应,并计算了误差。研究表明,该有限元模型在一定程度上可用于电磁-结构-流场的仿真分析,流速较小时,有限元仿真结果与实验误差较大;流速较大时,流场趋近于匀速场,仿真结果与实验结果误差较小。
[1] 吕殿龙,魏云飞,韦 旺,等.电磁流量计及其在聚驱测井中的应用[J].石油仪器(Petroleum Instrument),2001,15(3):34-36.
[2] 张文军.外流式电磁流量计在大庆油田聚驱注入剖面测井中的应用[J].国外油田工程(Foreign Oilfield Engineering),2004,20(8):35-37.
[3] MICHALSKI A,WINCENCIAK S.Method of optimization of primary transducer for electromagnetic flow meter[J].IEEE Instrumentation and Measurement Technology,1996,2:1 350-1 353.
[4] MICHALSKI A,STAEZYNSKI J,WINCENCIAK S.3 D approach to designing the excitation coil of an electromagnetic flowmeter[J].IEEE Transactions on Instrumentation and Measurement,2002,51(4):833-839.
[5] 金宁德,宗艳波,张玉辉,等.四电极电磁流量计磁场分布特性数值模拟[J].工业计量(Industrial Measurement),2009,19(2):2-6.
[6] 邬惠峰,严 义,吴红娉,等.基于 Ansys的电磁流量计建模研究[J].仪器仪表学报(Chinese Journal of Scientific Instrument),2008,29(2):372-376.
[7] 张志刚.外流式电磁流量计权重函数分布的仿真研究[J].石油仪器(Petroleum Instrument),2010,24(1):12-14.
[8] 班怀国,吴兰鹰,王令刚.关于ANSYS谱分析的二次开发[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2007,28(1):41-48.
[9] 王 彬,杨庆山.弱耦合算法的实现及其应用[J].工程力学(Engineering Mechanics),2008,25(12):48-59.
[10] 翟建华.计算流体力学(CFD)的通用软件[J].河北科技大学学报(Journal of Hebei University of Science and Technology),2005,26(2):160-165.
Simulation and experimental study on four-electrode outflow electromagnetic flowmeter
ZHANG Guang-yu,LIU Bao-long,LI Long-qiu
(School of Mechatronics Engineering,Harbin University of Technology,Harbin Heilongjiang 150001,China)
Four-electrode outflow electromagnetic flowmeter is a new logging equipment that can ideally measure the injection profile flow and is widely applied to the measurement of oilfield injection wells and polymer injection wells.At present,the study on electromagnetic flowmeter is only conducted in actual environments,which has a low efficiency and a high cost.A finite element model of a four-electrode outflow electromagnetic flowmeter is built in this work by using strong coupling method.The response and error analysis are performed at different flow velocities.The results show that the finite element model can be used for simulating the magnetic field in a four-electrode outflow electromagnetic flowmeter partly.It is also found that the error between the simulation and the experiment is larger at a low flow velocity than at high flow velocity.
electromagnetic flowmeter;finite element;strong coupling;multi-physics field
TH814+.93
A
1008-1542(2011)05-0441-05
2011-05-23;
2011-06-29;责任编辑:王士忠
张广玉(1962-),男,黑龙江哈尔滨人,教授,主要从事光机电一体化、空间机电系统技术方面的研究。

