一个含特殊函数的Hardy-Hilbert型不等式

黄裕建

(广东轻工职业技术学院教务处，广东广州 510300)

一个含特殊函数的Hardy-Hilbert型不等式

黄裕建

(广东轻工职业技术学院教务处，广东广州 510300)

通过引进一个0次齐次核并估算权函数，获得一个含Polygamma函数的具有最佳常数因子的Hardy-Hilbert型不等式.

Hardy-Hilbert型不等式;权函数;Hölder不等式;最佳常数因子;特殊函数

0 引言

19世纪初期，经过德国数学家HILBERT D、英国数学家HARDY G H和REISZ M等人的努力，建立了著名的Hardy-Hilbert不等式［1］:

Hardy-Hilbert不等式自创立100年来，吸引了不少数学家的关注及研究，对其做了大量的改进和推广等工作［2-5］.自1991年，沿用权系数方法和参量化方法，Hardy-Hilbert型不等式的发展经历了从-1齐次核到负数齐次核，再推广到实数齐次核与非齐次核［6-10］.

本文应用权函数的方法，建立了一个0次齐次的用特殊函数表示其最佳常数因子的Hardy-Hilbert不等式，并给出相应的等价形式.

1 引理

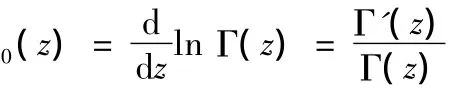
更进一步，Polygamma函数也可以定义为［12］，则有

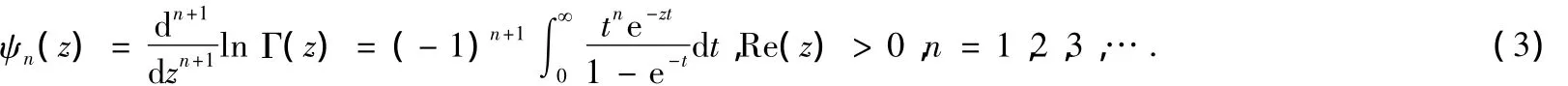
引理1设－1＜λ＜1，分别定义权函数φ(λ，x)与ψ(λ，y)为

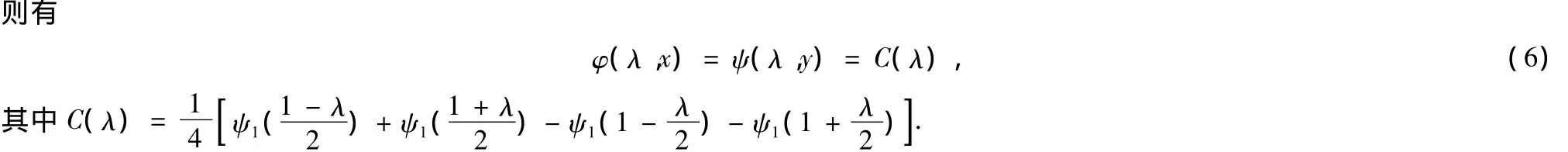
证明 配方，由带权的Hölder不等式［5］，对y∈(0，∞)，结合引理1，得

2 主要结果

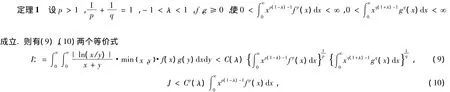
这里，常数因子C(λ)与Cp(λ)均为最佳值.

证明 若式(8)对某个y＞0取等号，则有不全为0的常数A，B，使

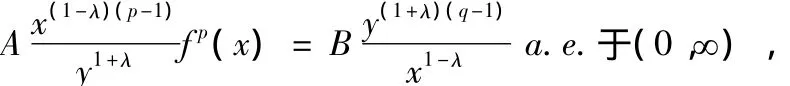
配方并由Hölder不等式［4］，得

由式(10)，得式(9).反之，设式(9)成立.令

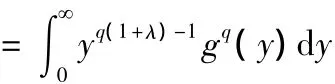
因此式(10)成立并与式(9)等价.

下证式(9)常数因子C(λ)是最佳的.事实上，任给ε＞0，令fε(x)=gε(x)=0，x∈(0，1);).若存在常数0＜k≤C(λ)，取代C(λ)后式(9)仍成立，代入fε(x)，gε(x)，则

由式(12)与(13)得C(λ)+ο(1)＜k，即C(λ)≤k(ε→0+).从而k=C(λ)为式(9)的最佳值.另外，式(10)的常数因子亦为最佳，否则由式(10)将得到式(9)的常数因子亦非最佳值，矛盾.证毕.

［1］ HARDY G H，LITTLEWOOD J E，POLYA G.Inequalities［M］.Cambridge:Cambridge University Press，1952.

［2］ MINTRINOVIC D S，PECARIC J E，FINK A M.Inequalities involving functions and their integrals and derivatives［M］.Boston:Kluwer Academic Publishers，1991.

［3］ 杨必成.算子范数与Hilbert型不等式［M］.北京:科学出版社，2009.

［4］ 胡克.解析不等式的若干问题［M］.2版.武汉:武汉大学出版社，2007.

［5］ 匡继昌.常用不等式［M］.济南:山东科学技术出版社，2004.

［6］ XU Lizhi，GUO Yongkang.Note on Hardy-Riesz’s extension of Hilbert’s inequality［J］.Chin Quart J Math，1991，6(1):75-77.

［7］ GAO Mingzhe，HSU L C.A survey of various refinements and generalizations of Hilbert’s inequalities［J］.J Math Res Exposition，2005，25(2): 227-243.

［8］ 杨必成.一个Hilbert型积分不等式［J］.浙江大学学报:理学版，2007，34(2):121-124.

［9］ YANG Bicheng.On Hilbert’s integral inequality［J］.J Math Anal Appl，1998(220):778-785.

［10］和炳，杨必成.一个核带超几何函数的0次齐次的Hilbert型积分不等式［J］.数学的实践与认识，2010，40(18):203-211.

［11］王竹溪，郭敦仁.特殊函数论［M］.北京:科学出版社，1979.

［12］RAINVILLE E D.Special Functions［M］.New York:Chelsea Publishing Company，1971.

A Hardy-Hilbert Type Inequality with a Special Function

HUANG Yu-jian

(Teaching Affairs Office，Guangdong Industry Technical College，Guangzhou510300，China)

By introducing a 0-homogeneous kernel and estimating the weight function，a Hardy-Hilbert type inequality with a Polygamma function and the best constant factor is obtained.

Hardy-Hilbert type inequality;weight function;Hölder’s inequality;best constant factor;special function

O178

A

1007-0834(2011)04-0010-03

10.3969/j.issn.1007-0834.2011.04.004

2011-09-05

广东省教育科学“十一五”规划资助项目(2010TJK137)

黄裕建(1969—)，女，广东河源人，广东轻工职业技术学院教务处副教授，主要研究方向:不等式及数学教育.