大学物理实验数据处理中不确定度的计算

盛 虹

(渭南师范学院,陕西渭南 714000)

大学物理实验数据处理中不确定度的计算

盛 虹

(渭南师范学院,陕西渭南 714000)

讨论了不确定度的概念与分类,针对物理实验数据处理过程中不确定度计算的难点进行分析讨论,提出了在大学物理实验数据处理中正确计算不确定度的方法.并以测钢丝杨氏模量为例介绍不确定度引入数据评定的具体做法。

不确定度;数据处理;测量结果

实验误差和数据处理是大学物理实验课程的重要学习内容之一。传统的误差理论是用“测量误差”的概念来评价测量结果的可信程度,真值一般不可知,测量误差(测量值N与真值之差)也不可知。应使用不确定度来评价测量结果。

1 不确定度的概念及分类

测量不确定度是说明测量结果的一个参数,表征合理赋予被测量值的分散性,它表示由于测量误差的存在而对被测量值不能确定的程度。不确定度的大小反映出测量结果的优劣。不确定度越小,则表示测量结果越接近真实值,其使用价值越高。在物理实验中,没有不确定度说明的实验结果是不完整的,甚至可以说是没有意义的。不确定度是概率意义上的误差范围,即随机误差分量和未定系统误差分量的联合分布范围。它可理解为一定概率的误差限值,即与一定置信概率相联系的误差分布基本宽度的一半。我们进行实验数据处理,计算和表达的通常是“不确定度分量”,而不是“误差”。不确定度一般含有多个分量,但按其数值的评定方法可归并成两类:A类和B类。A类分量:对同一物理量多次重复测量时用统计学方法计算的分量,称A类标准不确定度,用符号“S”或符号“ΔA”表示。B类分量:用非统计学的其他方法评定的分量,称B类标准不确定度,用符号“u”或“ΔB”表示。例如,仪器误差是一种未定系统误差,以估算方法评定的仪器误差是我们在物理实验中经常遇到的不确定度的B类分量[1]。

2 直接测量结果的不确定度

对某一物理量作多次等精度独立测量得x1、x2、……xn为测量值的算术平均值,直接把平均值的标准差Sx作为A类标准不确定度ΔA

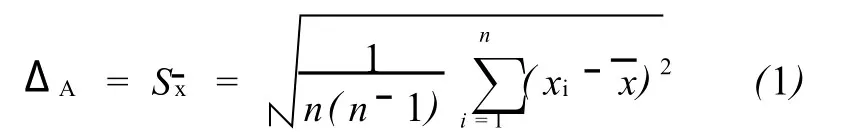
B类标准不确定度ΔB的数值主要来自以前的测量数据、有关的材料及仪器的特点、性能等,一般由仪器校准、制造说明书或其他证书以及手册等提供数据。与仪器不准对应的B类标准不确定度为[2]:

Δ仪表示仪器的最大误差限,C为置信系数。其取值为:仪器的误差服从均匀分布,C=;仪器的误差服从正态分布,C=3。在缺乏信息难以分清分布的情况下,以不确定度偏大的假设为准,一律按均匀分布来处理。

用符号“Δ”表示总不确定度,则有

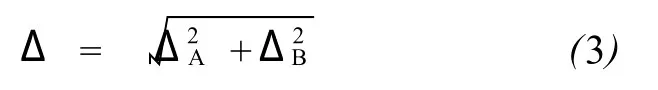
总不确定度Δ只取1至2位有效位数。由总不确定度决定测量结果的有效数字的位数。对单次测量的不确定度可以认为Δ=ΔB。

3 间接测量结果的不确定度

设被测量y可写成直接测量量的函数:

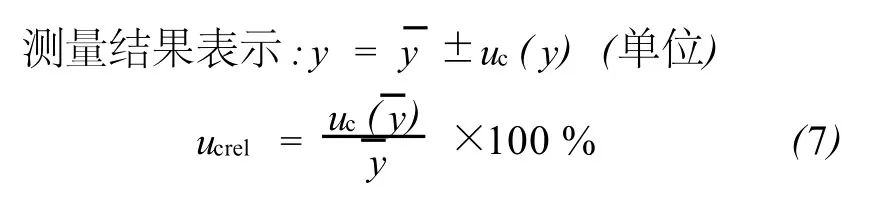
4 不确定度在普通物理实验数据处理中的应用

以“伸长法测钢丝杨氏模量”实验的数据处理为例,介绍测量不确定度的评定方法。

表1 金属丝直径的测量(零点读数:0.02mm,Δ仪=0.22mm)

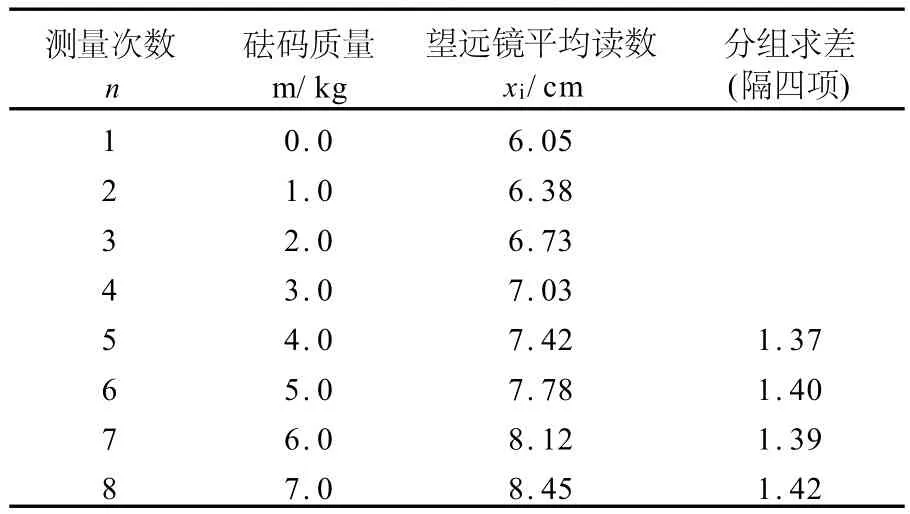
表2 金属丝微小伸长量的测量(Δ仪=0.5mm)

钢丝长度L=86.20 cm,截面积为S,光杠杆前后足尖距离d1=7.548cm,镜面到直横尺的距离d2=88.50 cm由分组逐差法求得:

[1]赵丽华,倪涌舟.大学物理实验[M].杭州:浙江大学出版社,2007.

[2]李慎安.测量结果与不确定度表示[J].中国计量,2002(12):37-38.

[3]贾翠红,赖恒,雷晋萍.测量不确定度及其估算[J].福建大学学报:自然版,2007(1):96-99.[4]刘丽群,曹文,王宏波.大学物理实验中误差理论教学的几点考虑[J].大学物理实验,2010,23(2):77-79.

Measure Uncertainty Counting and Applying in Normal Physics Experiment

SHENG Hong

(Weinan Teachers University,Shan’xi,Weinan 714000)

It discusses some conceptions and the classification about uncertainty.And analysed the difficult points in the process of dealing with data about uncertainty.Based on them,some methods of introducing and applying the uncertainty during the process of dealing with test data in normal physics experiment are alsOgiven here.Finally,Young modulus measuring method of metal wire is used tOillustrate the design methodology.

uncertainty;test result;handling of data

O241.1

A

1007-2934(2011)03-0092-03

2010-12-15