用Matlab软件模拟振动实验

喻力华,陈昌胜,刘书龙,项林川

(华中科技大学,湖北武汉 430074)

用Matlab软件模拟振动实验

喻力华,陈昌胜,刘书龙,项林川

(华中科技大学,湖北武汉 430074)

采用Matlab软件求解简谐振动、阻尼振动与受迫振动的微分方程,通过得到的位移-时间关系,来分析不同振动方式的物理特征。

Matlab软件;简谐振动;阻尼振动;受迫振动

振动是“大学物理”课程中的一个重要教学内容,在实际的课堂教学中通常采用一些演示实验来说明所涉及的物理概念,例如用关联单摆来演示共振现象,但某些重要的振动特性却较难通过实验来清晰地演示,如阻尼力对共振条件的影响等。由于振动的许多特征是由运动微分方程的解在不同参数的情况下表现出来的,而在“大学物理”课程中通常直接给出物体振动的位移表达式,因此,为了较清晰地演示和说明振动的特点,本文采用Matlab数学软件中的符号数学工具箱(SymbolicMathToolbox)求解振动微分方程,并且利用软件的作图功能直观地将振动的位移-时间关系显示出来,从而清晰地展示了许多振动的物理特征,这种方法是课堂演示实验的一种很好的补充。

1 振动微分方程的求解

以机械振动为例,物体振动微分方程的一般形式为[1]:

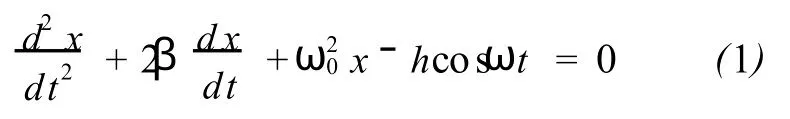
式中:x为物体的位移,t为时间,ω0为振动的固有圆频率,β为阻尼因子,反映阻尼力的大小(由阻尼系数和振子质量决定),h反映外强迫力的大小(由外强迫力振幅和振子质量决定),ω为周期性外强迫力的圆频率。若h=0,则为阻尼振动;若h=0,β=0,则为简谐振动;若h≠0,β≠0,则为受迫振动。

利用Matlab软件求解上述微分方程的语句如下[2]:

2 简谐振动与阻尼振动

当h=0时,β2＜ω20为弱阻尼振动;β2＞ω20为过阻尼振动,β2=ω20为临界阻尼振动,β=0为简谐振动。如图1所示,(a)为简谐振动,其他为弱阻尼振动。可以看出,简谐振动的振幅不变,而当阻尼因子增大时,弱阻尼振动的振幅随时间衰减得更快,并且从图中还可看出阻尼力的增大导致振动周期增大,这一特征很难通过实验演示。图2为弱阻尼、临界阻尼和过阻尼振动的比较,可以看出,临界阻尼和过阻尼振动由于阻尼力太大,使振子无法完成一次振动,只能逐渐趋近平衡位置。从图中可以清楚地看出,临界阻尼使振子最快回到平衡位置,因此在需要使振动尽快停止的实验装置中(如天平、电表表头),应该采用临界阻尼。

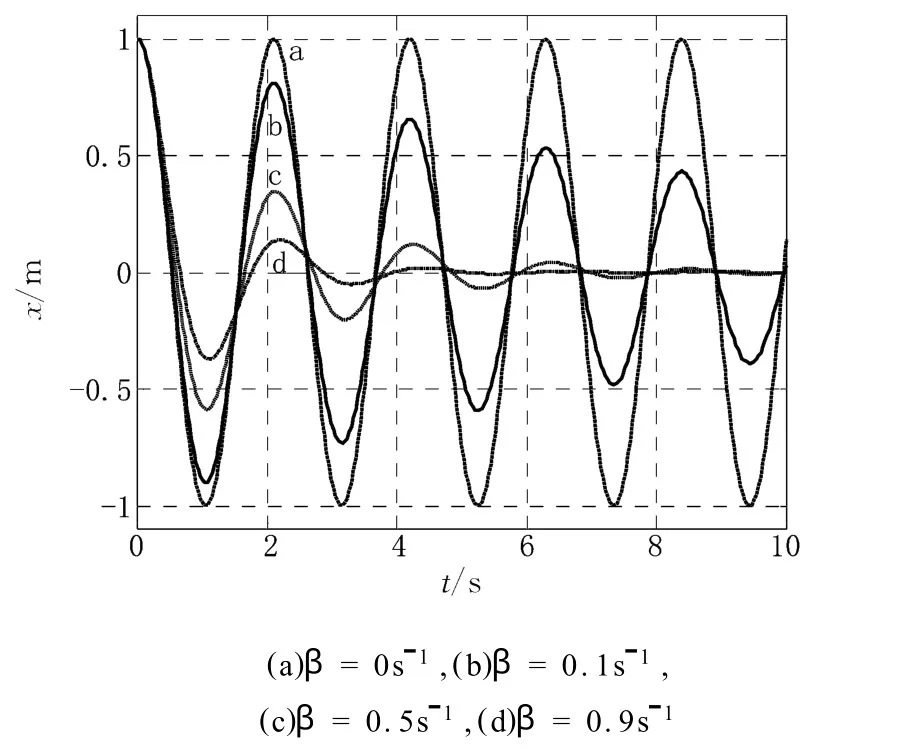
图1 简谐振动与弱阻尼振动

3 受迫振动

图3、图4分别为外强迫力频率小于和大于固有振动频率时的受迫振动。由于受迫振动的解由两项组成[1],其中一项振幅随时间指数衰减,在阻尼力很小的情况下,其频率主要由固有振动频率决定,另一项为振幅不变的简谐振动形式,其频率为外强迫力频率。可以看出,在两种外强迫力频率的情况下,经过一段时间,振动均逐渐趋近于外强迫力频率的简谐振动形式。图5为外强迫力频率等于固有振动频率的情况,由于阻尼力较小(β=0.1s1),根据振幅共振外强迫力频率需满足的条件[1]:

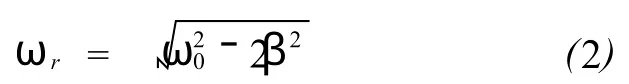
因此出现了明显的共振现象,其稳定振动的振幅明显大于图3、图4的情况。

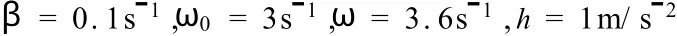
图3 受迫振动

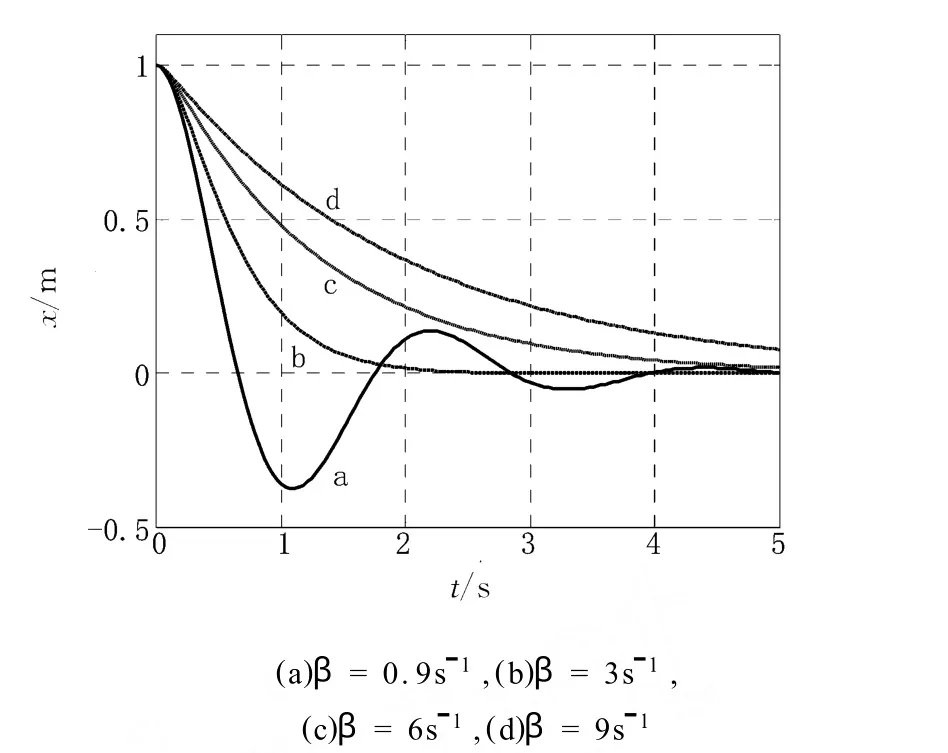
图2弱阻尼、临界阻尼和过阻尼振动

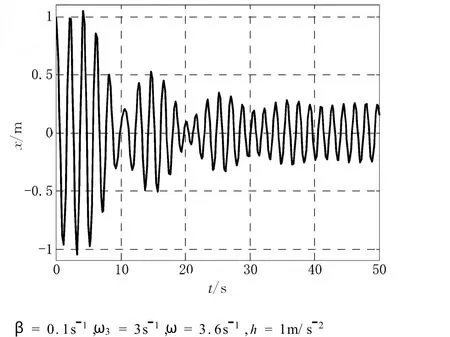
图4 受迫振动

图5 弱阻尼情况下的共振

图6为阻尼力较强情况下的共振。显然,由于阻尼因子较大,指数衰减项很快趋近于零,因此振动很快过渡为简谐振动的形式。根据(2)式,外强迫力圆频率ω=1s-1时满足振幅共振条件,这时的稳定振动振幅明显大于外强迫力圆频率等于固有振动频率的情况。

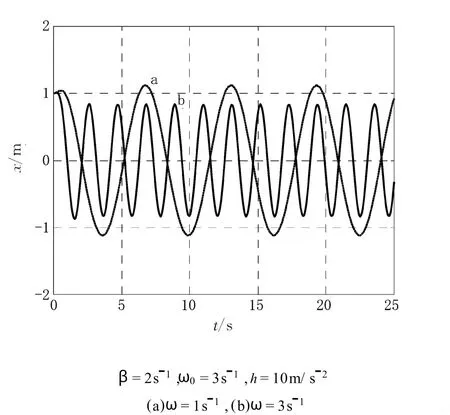
图6 强阻尼情况下的共振

4 总 结

通过以上讨论可以看出,利用Matlab软件求解振动微分方程,可以很容易地获得振动的一些基本特征,并可方便地修改相关参数来观察振动的变化,因此这种方法特别适合用于教学演示。

[1]张三慧.大学物理学[M].北京:清华大学出版社,1999.

[2]D.Hanselman,B.Littlefield.精通Matlab综合辅导与指南[M].李人厚,张平安,译.西安:西安交通大学出版社,1998.

Simulate the Oscillation Experiment by Matlab Soft ware

YU Li-hua ,CHEN Chang-sheng ,LIU Shu-long ,XIANG Lin-chuan

( Huazhong University of Science and Technology , Hubei ,Wuhan 430074)

:Using Matlab softw are the differential equations of simp le harmonic oscillation、damped os-cillation and forced oscillation are solved,the physical charactersof different oscillation modes are ana-lysed by the obtained relations betw een the disp lacement and time.

Matlab software;simple harmonic oscillation;damped oscillation;forced oscillation

O411.3

A

1007-2934(2011)03-0079-03

2010-10-17