圣安德烈斯断层南段大地震发生的准周期性＊

Katherine M Scharer,Glenn PBiasi,Ray JWeldon II,Tom E Fumal

1)Department of Geology,Appalachian State University,Boone,North Carolina 28608,USA

2)Seismological Labo rato ry,University of Nevada-Reno,Reno,Nevada 89557,USA

3)Department of Geological Sciences,University of Oregon,Eugene,Oregon 97405,USA

4)U.S.Geological Survey,M enlo Park,Califo rnia 94025,USA

圣安德烈斯断层南段大地震发生的准周期性＊

Katherine M Scharer1),Glenn PBiasi2),Ray JWeldon II3),Tom E Fumal4)

1)Department of Geology,Appalachian State University,Boone,North Carolina 28608,USA

2)Seismological Labo rato ry,University of Nevada-Reno,Reno,Nevada 89557,USA

3)Department of Geological Sciences,University of Oregon,Eugene,Oregon 97405,USA

4)U.S.Geological Survey,M enlo Park,Califo rnia 94025,USA

圣安德烈斯断层(美国加州)南段最后一次大地震距今已有153年了,而其平均震间间隔却仅为～100年。如果大地震的复发具有周期性,而并非随机发生或群集发生,则这个时间长度是很值得关注的,而且通常意味着概率意义上的地震危险性增大。遗憾的是,多数地震记录都很简单,这就限制了对单条断层上地震复发的分布特征的描述。本文利用加州W rightwood 3000年中29次有地面破裂的地震的综合记录进行统计检验。结果表明此处地震的复发远比依据泊松分布预测的结果更具规律性,而且也不呈群集分布,由此,我们推断地震的复发具有准周期性。基于观测的敏感性分析对可供选择的地质记录解释进行严格检验,结果揭示出持续的单峰时间依从特征。这一结果为利用更新模型来正式预测圣安德烈斯断层南段未来地震概率提供了有力的支持。根据记录,仅有4个间隔(15%)长于目前的开放间隔,由此凸显了该断层当前地震形势的严峻性。

引言

地震灾害预测对地震减灾经费的分配、保险费率和建筑规范等都起到影响作用。这种预测在很大程度上受控于大地震的平均间隔以及描述地震复发特征的分布形态[1-6],而目前根据仪器或历史记录对地震的复发特征了解得还很少。例如在南加州,圣安德烈斯断层上震级大于7级的历史记录就包含两次间隔仅大于44年的地震(分别发生在1812年和1857年),而随后便是至今153年的空白。圣安德烈斯断层上在短时间内地震密集发生与长时间间隔共存的现象,是全球范围内断层地震活动的典型特征,由此引发了人们研究史前地震(古地震)的兴趣,这样才能延长地震年表的时间跨度(如文献[7-9])。地震记录的时间越长,对地震复发分布的估算便会更加稳健,而且可以将非时间依从的复发分布和时间依从的复发分布区别开来。

非时间依从特征通常可以用泊松分布模型描述,该模型所描述的事件在时间上具有随机性和独立性特征[10]。泊松分布得出的是未来地震的条件概率,这种概率几乎是不随时间而变的。相对于单个地震引起的应力松弛而言,如果断层的应力范围很大,那么地震的复发就是随机的[11],且时间的测定受控于多种随机或瞬变过程,如地震触发或断层间应力相互作用等[2,12,4,13]。相比之下,单峰时间依从复发模型的典型特征为,震后即刻出现的条件概率很低,但随着平均时间间隔的逼近,条件概率迅速增大。常见的例子包括对数正态分布和布朗过程时间(B row nian Passage Time)分布[14-15,3]。这些分布已经被用于弹性回跳理论模型,该理论认为弹性能量通过邻近地块的持续远场运动而不断积累,直至应力水平达到临界状态,能量在一次地震中得以释放。利用古地震记录对时间依从特征进行的探讨主要集中在对平均复发时间周围间隔离散度的研究上[16,1,14,17-19]。通常情况下可以观测到某种单峰时间依从的复发特征,但克服古地震记录所固有的不确定性仍然是一种挑战,这主要是由于大多数记录资料还过于简单[18-19]。

1 方法

本研究中,我们基于一种现有的方法,将年代测定的不确定因素正式纳入每个时间间隔的概率分布函数(PDF)(图1;文献[16]),并将该方法应用于发表时间最长的古地震记录中。W rightwood记录包含了两个时段(即公元前3000—1500年和公元500年至今,分别被称为老时段和新时段)发生的28次古地震的详细证据(图1;文献[20-23,11])。现在已经知道在这2000年期间发生了哪些地震,但该时段的野外调查研究和年代测定尚未完成。我们结合新、老时间段的平均间隔,建立了一个地震主年表。

我们还考虑了一个现有研究中未曾关注的问题,即与古地震证据解释相关的不确定因素(图2)。复杂的断裂模式和沉积模式所产生的地质结构可能酷似古地震证据,也可能掩盖古地震证据,从而导致了某些真正的地震事件被遗漏,而另一些不是地震的迹象又被错误地归于地震证据(图2;文献[24,22])。为检验统计结果对各种解释的敏感性,我们为主年表建立了35个可选序列,其中证据不充分的地震被剔除,相反,一些假定缺失的地震事件被添加到分辨率较低的时段(图1)(有关各年表中地震的采纳情况及参数的详细资料见美国地质学会(GSA)数据库①GSA数据库2010155条可通过下列渠道获取:(1)www.geosociety.org/pubs/ft2010.htm;(2)editing@geosociety.org;(3)Documents Secretary,GSA,P.O.Box 9140,Boulder,CO 80301,USA。该条目包含每一年表中平均间隔的比较,对不同置信度的KS测试结果的检验,以及每一年表中地震的采纳情况、复发参数和统计结果等。DR1数据列表)。

基于对地震质量的评定[22],主年表中证据模糊的地震(图1中绿色PDF)被相继删除,这就使其余地震的间隔变长。因为其中两次地震距观测资料有限的老时段的基点较近,所以我们也对年代较轻的11次地震进行了研究,由此提供连续的较高质量地震序列。为了对可能遗漏的地震的影响进行评估,5次假定地震被依次添加至因沉积速率低而不能识别地震破裂的地层中。例如,从公元前1300年到1475年这一时间段,在W rightwood没有碎屑沉积的记录。而这段时间内,在邻近的古地震地点却出现破裂记录(图1;文献[25-26,11])。我们认为[11]该破裂贯穿所有3个地点,但却没有在W rightwood留下能与随后的一次地震明确区分的证据,因此,我们将Pallet Creek T事件(PCT)作为第29次W rightwood地震考虑在内(图1中的PCT)。同样,某些W rightwood史前地震的证据以生长地层的形式出现。如果地震使得地面凹陷加深,而地槽又充满了薄薄的沉积,则很有可能分辨不出地震事件[22]。鉴于此,我们在只有薄沉积层存在的一些时段依次加入了4次假设地震(采用的概率分布函数PDF的格式为W 410),并检验其对地震序列的影响(图1)。

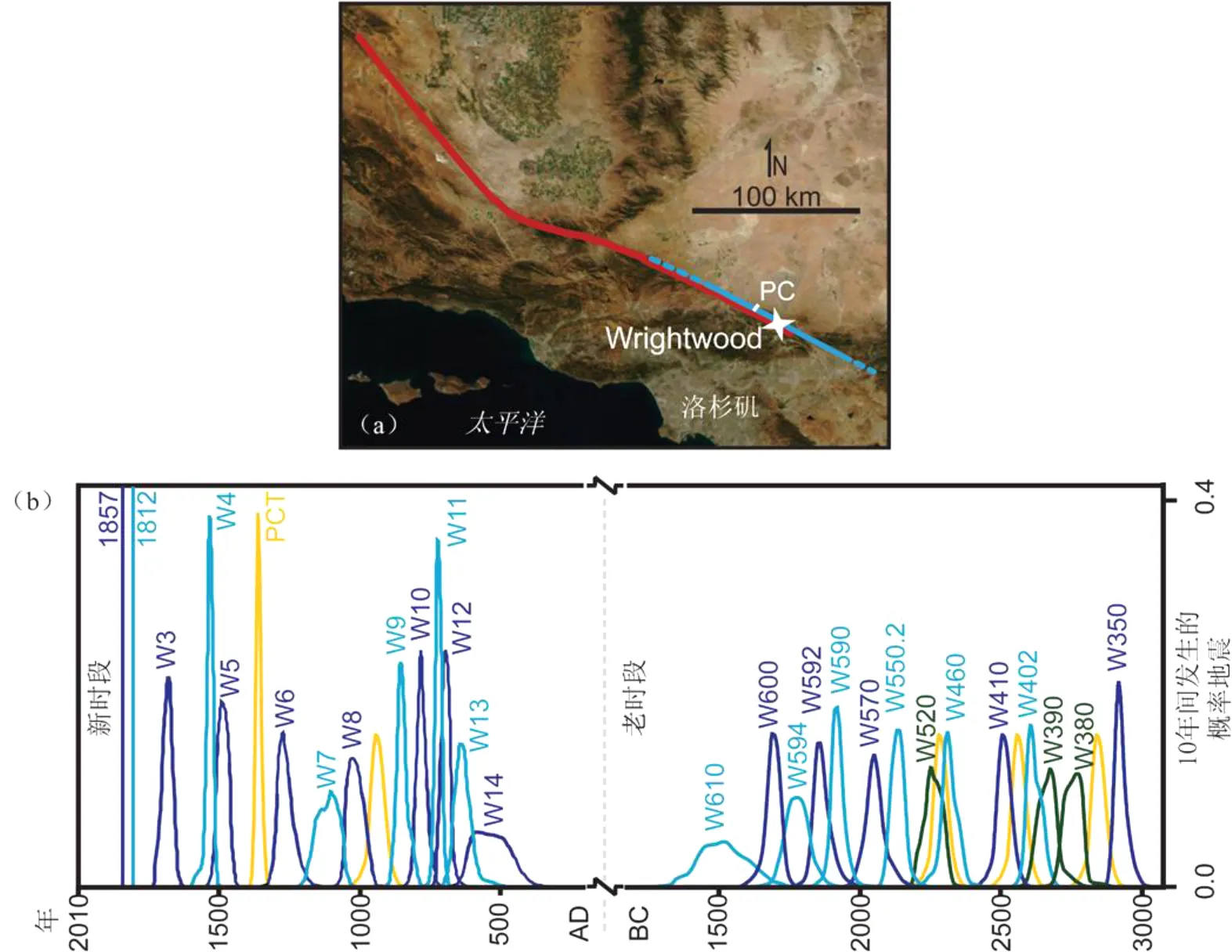
图1 Wrightwood古地震遗址的位置及古地震。(a)南加州卫星图像,显示出1812年地震(蓝线)和1857年地震(红线)相对于Wrightwood古地震遗址(星号)的范围。PC—Pallett Creek。(这是通过美国农业部林业局遥感应用中心获得的美国国家航空航天局卫星图像)。(b)Wrightwood古地震年代的概率分布函数(PDF);在Wrightwood记载的史前地震均以W开头;历史地震直接标注年代。PDF用相间的蓝色表示;绿色PDF表示可能的地震[22]。黄色PDF是假设的地震。PDF源自贝叶斯定理对可以划定地震界限的放射性碳年代测定与地层年代测定中不确定性的处理[16]。由于年代测定的局限性,PDF出现部分重叠现象;但清晰的地层学证据表明每次地震都是一个独立事件

通过从每一地震PDF中随机抽取的方式,将地震日期的不确定性考虑在内,以生成地震年表中每一间隔的PDF(PDF间隔范围示于图3;文献[16])。每个年表中的复发参数通过对地震PDF进行1000次取样来确定,由此,地震事件年代测定的不确定性被直接纳入参数估算中。当新、老时段被分别评估时,排除某些特定地震事件会使平均间隔值发生几十年尺度的变化,从而影响对于地震危险性的评估。这些结果突出显示了评估地震数据质量的重要性,以及将评级体制纳入地震危险性评估逻辑树的潜在价值。根据综合记录得出的重要结论是,如果序列很长,单个地震是否被考虑在内并不十分重要:只有当分别剔除或添加多达5个地震时,平均间隔才会稍稍增大或减小(≤15年)(图DR1)。

为了检验随机分布模型和时间依从分布模型究竟哪一个能更好地描述W rightwood年表,我们采用了Kolmogorov-Smirnov(KS)拟合优度检验。这些非参数统计检验将经验数据比作已知分布的累积分布函数。KS统计数值是两个函数之间的最大差值。

图2 Wrightwood古地震的高质量证据与低质量证据的对比。(a)终止于开放裂隙处的断层线尺度和形状都类似于现代裂隙,极有可能由同震地面形变引起。被破裂错断(箭头)的最年轻地层上方的砾石沉积物填满了裂隙,也提供了地震时的地表证据。(b)简单的断层线显示出模糊破裂证据。引起下部单元大规模错位的横向滑移明确显示出地震证据,但朝断层线顶部很小的错位则可能缘于向上位移减小,也可能缘于该断层线上滑动量很小的后续地震,由此导致地震界限模糊不清。每张照片的高度是1.5 m

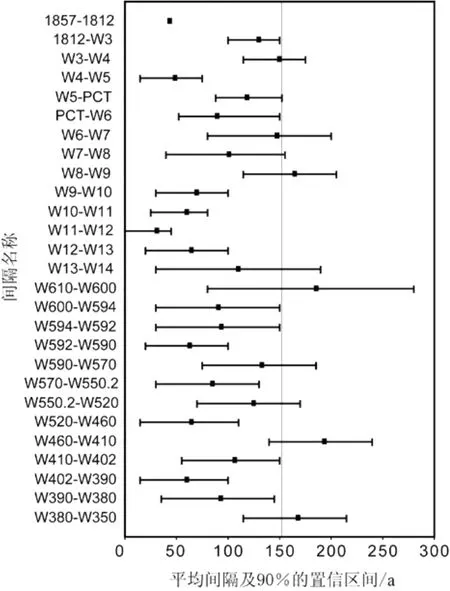
图3 主年表中每一间隔与目前153年开放间隔(灰色线段)的比较。平均间隔长度大都为＞～70年,只有4个间隔长于目前的间隔

我们利用由Biasi等[16]提供的两个独立的KS检测,将泊松分布作为零假设,因为它对应于随机时间的地震复发,而且以单一参数(即平均间隔)为特点。我们用蒙特卡罗(Monte Carlo)方法对每个年表进行200次抽样,以保持地震年代PDF的不确定性,并报告出各年表中在各种置信水平下均不符合泊松分布的采样百分比(图DR2)。

2 结果与讨论

第一个KS检验利用了从非时间依从序列中随机选取的间隔长度会呈指数分布的特征(图4a)。与之相反,从单峰时间依从分布中随机选取的间隔则主要集中在该分布模式附近。这种检验显示,在置信水平很高的情况下,主年表呈现出单峰时间依从的有力证据(图4d),且所有综合年表都不大可能满足泊松过程。具体而言,在置信度为80%时,＞90%的检验都是失败的(图4d;图DR2)。这些结果的说服力得益于综合序列的长度,而如果分别对其进行研究,则新、老时段的长度较短,也就没有如此强的说服力(图4D;表DR2)。

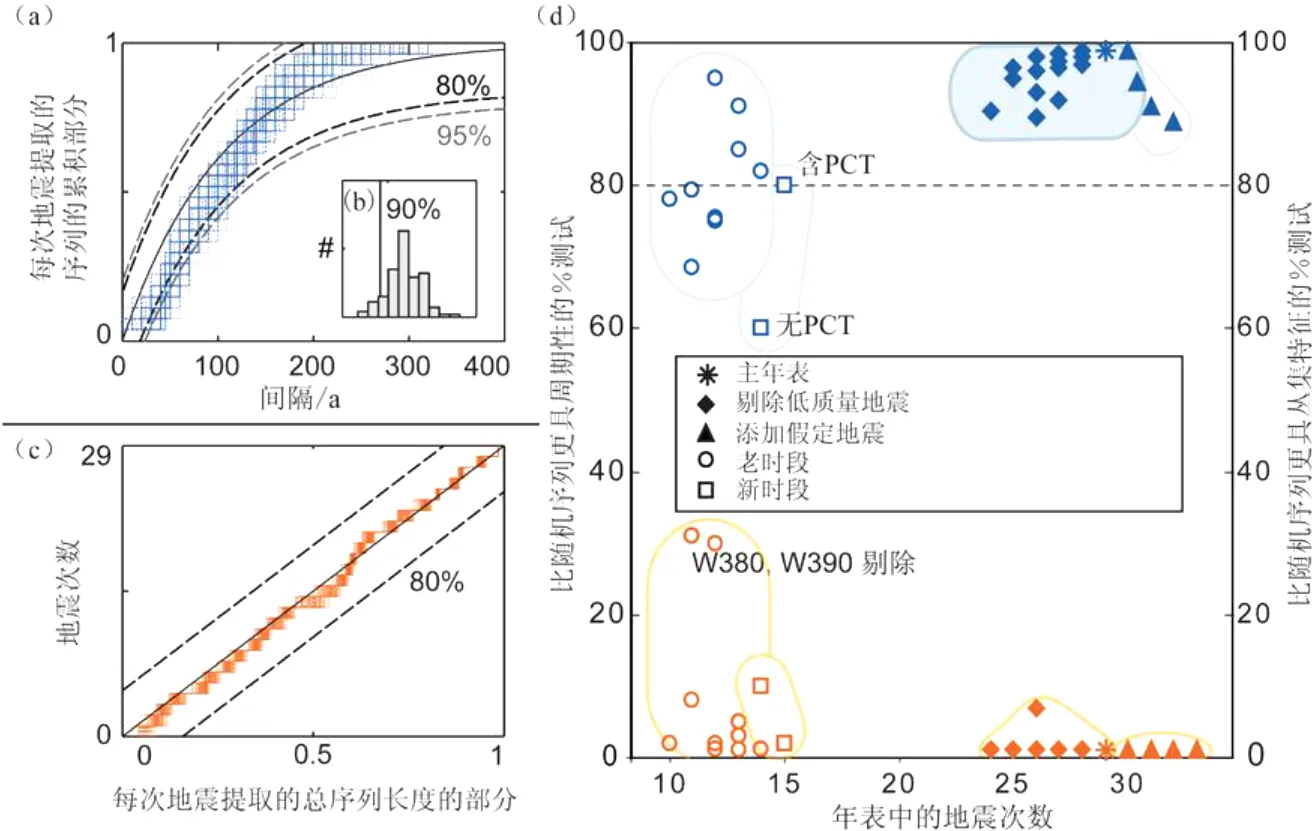
图4 统计结果。(a)主年表周期性行为的检验,将序列中200个结果(蓝线)与指数分布(黑色实线)进行比较;置信区间之外的实现值(虚线)不符合这一水平的泊松分布。由于平均值(～100年)附近的间隔数量超过了根据相应指数分布预期的数量,所以对该序列的检验多次失败。(b)置信度柱状图,200个样本实现值中没有一个通过这一置信度的检验。这些样本实现值中,95%的在置信度为90%时未通过检验(黑线)。(c)KS丛集性检验显示从主年表中顺次选取的200个样本(橘黄线)。如果连续数个间隔远远短于或长于平均值,则每个实现值都有可能超过置信区间(虚线),因而通不过检验。(d)KS测试结果汇总,显示周期性(蓝色)或丛集性(橘黄色)太强,不可能源自80%置信度随机分布的测试百分比。对综合古地震记录(表DR2)所有可供选择的合理解释得出的共同结论是,Wrightwood复发间隔含有显著的单峰时间依从特征,而没有明显的丛集特征的证据。PCT—Pallet Creek T事件

第二个KS检验的目的是探测时间变化特征,在古地震研究中通常被描述为“丛集”特征,此时可以观测到很短或很长的复发间隔(如文献[26])。与丛集序列相比,取自泊松分布的样本不会产生大量类似的连续抽取的短间隔或长间隔(图4c)。从区别于序列平均值的持续的时间变化意义上讲,在所有的综合年表中均未观测到丛集特征(图4d;表DR2)。

对单峰时间依从特征的另一个支持证据源于方差系数(COV)的测试。对数正态分布的COV与对数均值的标准差有关(表DR2;文献[1])。具有完全周期特征的序列其COV是零,但随着序列的规则性变差,COV逐渐增大。综合序列的对数正态COV约为0.7(表DR2),表明其时间依从特征很弱,但这一数值还是略高于先前对圣安德烈斯断层该段的评估结果[14,19]。由于放射性碳测年结果的不确定性,COV在一定程度上会升高,这是因为放射性碳的不确定性会导致每一间隔PDF的不确定性,由此,标准差也就大于纯粹源自事件发生年代的固有变化。

我们分析了[11]W rightwood年代较轻的区段内位错量与地震发生时间的关系。这项工作得出的一个有趣的结果是,公元600—900年间的视滑动速率提高了3倍,这是由于在复发间隔较短的地震期间发生了一系列大于平均位错的滑动。对于较长的综合记录,这一系列事件并非与序列的自然变化不符。相反,我们发现该系列事件符合单峰时间依从复发特征。我们认为地震复发的间隔尺度是有适度变化的,但也有一个集中趋势,表明断层基本受控于一个更新过程。平均间隔的可变性缘于断层的特征,或缘于该断层与其他断层的相互作用[27-28],但某种最小应变积累也具有典型意义(约50年;图3)。滑移量的变化不仅会使间隔尺度发生变化,而且还会使地震震级有所不同(根据文献[29]的平均位移关系,这些地震的震级为M 6.8～7.9)。然而,鉴于沿破裂迹线的可变性(如文献[30]),我们认为要对断层习性有更好的认识,就必须整合整条断层上的多处古地震观测数据,以重建完整的断层破裂史。

主年表的对数正态平均间隔为86年(间隔68～109年的占95%)(图DR1;表DR1)。考虑到未来的地震危险,目前的开放间隔长度极不寻常。虽然主年表中4个间隔的平均值较长,但153年在南加州地区没有发生一次大地震,这一时间段使其超出了以往许多间隔(66%)的90%的置信限度(图3)。时间依从模型对于未来地震的条件概率意义重大。利用对数正态分布模型估算,一次大地震的30年条件概率比随机时间的假设得到的估算值高出35%(95%的范围是20%～47%),或75%(表DR2)。这些结果为利用单峰时间依从分布正式预测圣安德烈斯断层地震危险性提供了有力的支持[2,6]。

(注:①原图除图3外,其余均为彩图;②图DR1、DR2、表DR1、DR2见网上资料:ftp:∥rock.geosociety.org/pub/reposit/2010/2010155.pdf)

译自:Geology,June 2010,555-558

原题:Quasi-periodic recurrence of large earthquakes on the southern San Andreas fault

(山东省地震局 梁凯利, 赵菡姿 译;陈时军,左玉玲 校)

(译者电子信箱,梁凯利:kaili568@sohu.com)

[1] Cramer C H,Petersen M D,Cao T,et al.A time-dependent p robabilistic seismic-hazard model for California.Bull.Seis.Soc.Am.,2000,90(1):1-21

[2] Field E H.A summary of p revious wo rking groups on California earthquake p robabilities.Bull.Seis.Soc.Am.,2007,97(4):1033-1053

[3] Nishenko S P,Buland R.A generic recurrence interval distribution for earthquake fo recasting.Bull.Seis.Soc.Am.,1987,77(4):1382-1399

[4] Parsons T,Toda S,Stein R S,et al.Heightened odds of large earthquakes near Istanbul:An interaction-based p robability calculation.Science,2000,288(5466):661-665

[5] Petersen M D,Frankel A D,Harmsen S C,et al.Documentation for the 2008 update of the United States national seismic hazard maps.U.S.Geological Survey Open-File Report 2008-1128,2008,61 p

[6] 2007 Working Group on Califo rnia Earthquake Probabilities.The unifo rm California earthquake rup ture fo recast,version 2(UCERF 2).U.S.Geological Survey Open-File Repo rt 2007-1437,2008,104 p

[7] Begin ZB,Steinberg D M,Ichinose GA,et al.A 40000 year unchanging seism ic regime in the Dead Sea rift.Geology,2005,33(4):257-260

[8] Weldon R J,Fumal T E,Biasi G P,et al.Past and future earthquakes on the San Andreas fault.Science,2005,308(5724):966-967

[9] Wells A,Goff J.Coastal dunes in Westland,New Zealand,p rovide a record of paleoseismic activity on the A lpine fault.Geology,2007,35(8):731-734

[10] Larson H J.Introduction to p robability theory and statistical inference.New Yo rk,John Wiley and Sons,1982,637 p

[11]Weldon R J,Scharer K M,Fumal T E,et al.W rightwood and the earthquake cycle:W hat a long recurrence reco rd tells us about how faults work.GSA Today,2004,14:4-10

[12] Harris R A.Stress triggers,stress shadow s,and seismic hazard.In:Lee W,Kanamo ri H,Jennings P,et al(eds.),International Handbook of Earthquake and Engineering Seismology,Part B.San Diego,Academic Press,2002:1217-1232

[13] Wyss M,Wiemer S.Change in the p robability fo r earthquakes in southern Califo rnia due to the Landers magnitude 7.3 earthquake.Science,2000,290(5495):1334-1338

[14] Ellswo rth W L,M atthews M V,Nadeau R M,et al.A physically based earthquake recurrence model for estimation of long-term earthquake probabilities.U.S.Geological Survey Open-File Report 99-522,1999,22 p

[15] Matthew s M V,Ellswo rth W L,Reasenberg P A.A brow nian model for recurrent earthquakes.Bull.Seis.Soc.Am.,2002,92(6):2233-2250

[16] Biasi G P,Weldon R J,Fumal T E,et al.Paleoseismic event dating and the conditional probability of large earthquakes on the southern San Andreas fault,California.Bull.Seis.Soc.Am.,2002,92(7):2 761-2781

[17] Ogata Y.Estimating the hazard of rup ture using uncertain times of paleoearthquakes.Journal of Geophysical Research,1999,104(B8):17995-18014

[18] Parsons T.Earthquake recurrence on the south Hayward fault ismost consistent w ith a time dependent,renewal p rocess.Geophysical Research Letters,2008,35:L21301,doi:10.1029/2008GL035887

[19] Sykes L R,Menke W.Repeat times of large earthquakes:Implications for earthquake mechanics and long-term p rediction.Bull.Seis.Soc.Am.,2006,96(5):1569-1596

[20] Fumal T E,Schwartz D P,Pezzopane S K,et al.A 100-year average recurrence interval for the San Andreas fault at Wrightwood,California.Science,1993,259(5092):199-203

[21] Fumal T E,Weldon R J,Biasi G P,et al.Evidence for large earthquakeson the San Andreas fault at the Wrightwood,Califo rnia,paleoseismic site:AD 500 to p resent.Bull.Seis.Soc.Am.,2002,92(7):2726-2760

[22] Scharer K M,Weldon R J,Fumal T E,et al.Paleoearthquakes on the southern San Andreas fault,Wrightwood,CA 3000 to 1500 B.C.:A new method fo r evaluating paleoseismic evidence and earthquake ho rizons.Bull.Seis.Soc.Am.,2007,97(4):1054-1093

[23] Weldon R J,Fumal T E,Powers T J,et al.Structure and earthquake offsetson the San Andreas fault at the Wrightwood,California,paleoseismic site.Bull.Seis.Soc.Am.,2002,92(7):2704-2725

[24] Bonilla M G,Lienkaemper J J.Facto rs affecting the recognition of faults exposed in exploratory trenches.U.S.Geological Survey Bulletin 1947,54 p

[25] Seitz G,Biasi G P,Weldon R W.An imp roved paleoseismic reco rd of the San Andreas fault at Pitman Canyon.In:Noller J S,Sowers JM,LettisW R(eds.),Quaternary Geochronology:Methods and Applications.American Geophysical Union Reference Shelf 4,2000:563-566

[26] Sieh K,Stuiver M,Brillinger D.A more p recise chronology of earthquakes p roduced by the San Andreas fault in southern Califo rnia.Journal of Geophysical Research,1989,94(B1):603-623

[27] Palmer R,Weldon RW,Humphreys E,et al.Earthquake recurrence on the southern San Andreas modulated by fault-normal stress.Geophysical Research Letters,1995,22(5):535-538

[28] Tentho rey E,Cox S F,Todd H F.Evolution of strength recovery and permeability during fluid-rock reaction in experimental fault zones.Earth and Planetary Science Letters,2003,206(1-2):161-172

[29] Biasi G P,Weldon R J.Estimating surface rupture length and magnitude of paleoearthquakes from point measurements of rupture displacement.Bull.Seis.Soc.Am.,2006,96(5):1612-1623

[30] Wesnousky.Displacement and geometrical characteristics of earthquake surface ruptures:Issues and implications for seismic-hazard analysis and the process of earthquake rupture.Bull.Seis.Soc.Am.,2008,98(4):1609-1632

P315.08;

A;

10.3969/j.issn.0235-4975.2011.08.004

2010-09-14。