再论粗粒土剪胀性模型

程展林，陈 鸥，2，左永振，丁红顺

再论粗粒土剪胀性模型

程展林1，陈 鸥1，2，左永振1，丁红顺1

（1.长江科学院水利部岩土力学与工程重点实验室，武汉 430010；2.河海大学水利水电工程学院，南京 210098）

介绍了2种堆石料大型三轴试验和平面应变试验的试验成果。假设土的应变分为弹性应变和剪胀应变，弹性应变与应力间服从广义虎克定律，剪胀应变服从Rowe剪胀方程，弹性泊松比为常数，完整地建立3参量Kp，Kq，G与应力关系式，初步提出了一种新的非线性剪胀模型，给出了模型参数的整理方法，论证了一般非线性弹性模型中泊松比的力学意义。试验表明，剪胀性模型能够很好地模拟堆石料的应力应变曲线，对于同一种堆石料，由三轴试验和平面应变试验得到的模型参数除强度指标外，其它参数有很好的一致性，并给出了2种堆石料的模型参数。该模型是一种力学概念明确，简单实用的非线性剪胀模型。

应力应变关系；本构模型；平面应变试验；剪胀性；粗粒土；土石坝

1 概 述

建立一种能突出土的主要特性，力学概念简单，参数物理意义明确且不同土体间参数具有可比性的本构模型是本文作者长期追求的目标，笔者在文献［1］中给出的剪胀性模型基本达到了这一要求。该剪胀性模型实际上是一个非线性3参量（体变模量Kp、剪胀模量Kq、剪切模量G）模型，类似的模型早在上世纪70－80年代已被提出并用于工程数值分析［2，3］。1993年，清华大学高莲士等人根据堆石料不同应力路径下三轴试验结果，提出一种非线性解耦K-G模型，并用在西北口面板坝应力变形计算上［4］。毫无疑问，要建立一个新的非线性3参量模型，关键问题是在3参量模型的基本框架下建立更加合理的Kp，Kq，G与应力状态的关系。

笔者近期针对2种堆石料，同时进行了大型三轴和平面应变试验，对本文作者以往提出的剪胀性模型［1］进行了深入分析，并进行了少量修正。研究发现，剪胀性模型不仅能很好地模拟粗粒土三轴和平面应变试验的应力应变关系曲线，而且，同一种粗粒土不同试验的模型参数有很好的一致性。本文将介绍有关试验成果及修正后的剪胀性模型。

2 试验及试验成果

2.1 试样的物理性质

试验用料为2个堆石坝工程的堆石料，为叙述方便简称为MS堆石料和QP堆石料，其试验级配曲线如图1。MS堆石料为辉石角闪岩料，最大干密度为2.445 t／m3，试验干密度为2.274 t／m3；QP堆石料为斑晶花岗片麻岩料，最大干密度为2.118 t／m3，试验干密度为1.927 t／m3。

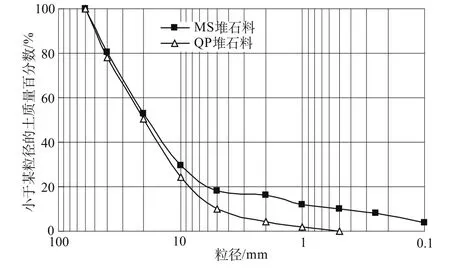
图1 堆石料试验级配Fig.1 Gradation of coarse-grained soils

三轴试验的试样尺寸为Φ300×H600 mm，本次试验的小主应力最大值为2.4 MPa。平面应变试验的试样为方样，尺寸为300 mm×600 mm×600 mm，本次试验的小主应力最大值为1.8 MPa。平面应变试验的试验程序是先在3个方向加小主应力，变形稳定后，在小主应力恒定条件下，按一定加荷速率施加大主应力至剪切破坏，在不同时刻测读轴向变形、体变、大主应力、中主应力。的堆石料不具剪胀性，大量的类似于文献［2］中的等静水压力剪切试验成果能证明这一点。

2.2 试验成果及分析

4组试验成果如图2、图3所示，同时给出了剪胀性模型的拟合曲线。关于模型拟合问题下文再谈，这里仅简单分析堆石料应力应变实测成果。从图2、图3可以看出：对于密度较高的MS堆石料，在σ3较小时，剪切过程中具有体胀特征，偏应力曲线具有应变软化现象，平面应变试验表现得更加明显；对于密度较小的QP堆石料，剪切过程中偏应力曲线为应变硬化，普遍表现为体缩，当应力达到强度值后，试样表现为等体积变形。值得一提的是，这不能说明密度较小

3 非线性剪胀模型

本文作者在长期的堆石料试验过程中，发现堆石料具有明显的剪胀性，且堆石料的剪胀应变较好地服从Rowe剪胀方程，因此，提出了粗粒土剪胀性模型［1］，近期研究发现该模型不尽合理，故重新推导如下。

3.1 剪胀模型的应力应变关系

为考虑剪应力对体变的影响，应力应变关系增量形式为：

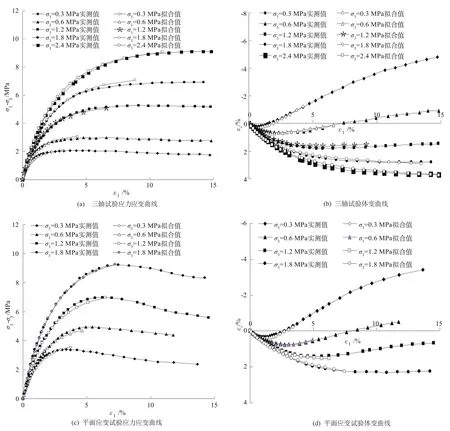
图2 MS堆石料三轴和平面应变试验成果Fig.2 Results of MStriaxial and plane strain test

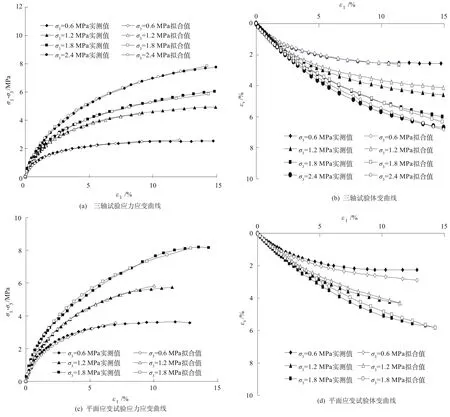
图3 QP堆石料三轴和平面应变试验成果Fig.3 Results of QP triaxial and plane strain test

式中：Kp，Kq，G分别为体变模量、剪胀模量、剪切模量；p，q为平均应力和广义剪应力；εv，εs为体应变和广义剪应变。

三轴压缩试验时，有下列换算关系：

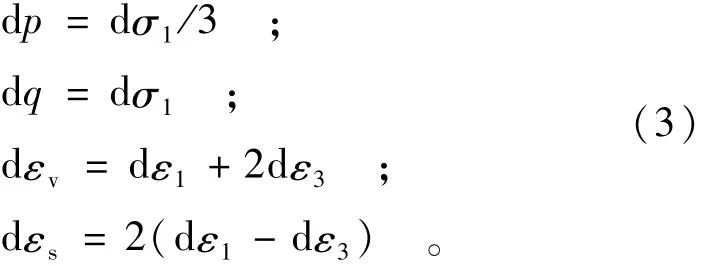
为确定Kp，Kq，G与应力状态的关系，假设土体应变分为弹性应变和剪胀应变，并用上标e和q表示。

弹性应变与应力间服从广义虎克定律，剪胀应变服从 Rowe剪胀方程［1］：

假定弹性泊松比μ为常数［1］。基于常规三轴压缩试验，模量Kp，Kq，G与应力状态的关系式推导见下节（3.2～3.4）。

3.2 体变模量Kp

体变模量Kp反映弹性体应变与应力p的关系，由虎克定律有如下关系：

式中μ为弹性泊松比，Eur为土的弹性模量，可由邓肯-张模型按下式计算：

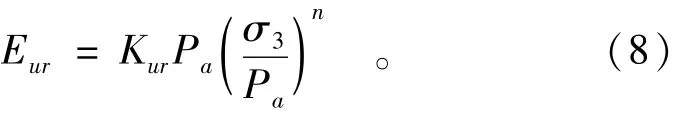
式中Kur和n为退荷再加荷试验确定的模型参数。

3.3 剪胀模量Kq

由Rowe剪胀方程，在三轴试验应力条件下，剪胀应变有如下关系：

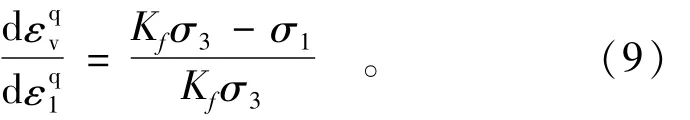
式中Kf为土体的最小能比值，为试验确定的模型参数。大量的粗粒土三轴试验表明，同一种材料的Kf为一常数，不随应力状态改变而变化［1］。

同样，三轴试验竖向应变可分为竖向弹性应变和竖向剪胀应变，即：

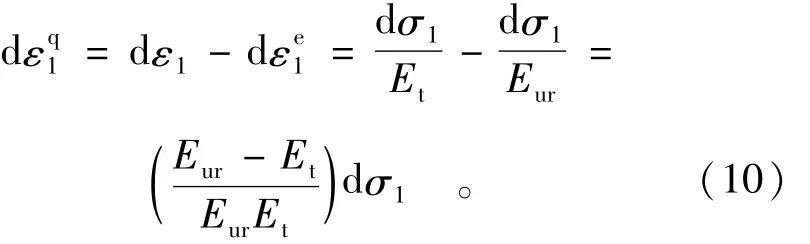
式中 Et切线模量，可采用邓肯-张模型的表达式［5］，本文认为，对于粗粒土，有必要对邓肯-张模型Et表达式进行修正（见3.5节）。在三轴试验应力条件下，有如下关系：

联立式（9）、（10）、（11），可得剪胀模量 Kq表达式：

3.4 剪切模量G

在三轴试验应力条件下，有如下关系：

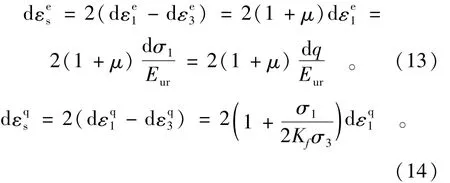
联立式（2）、（5）、（10）、（11）、（13）、（14），可得剪切模量G表达式：

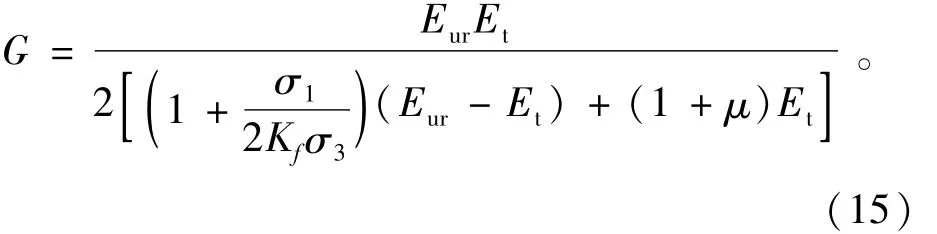
3.5 切线模量E t

在剪胀模量表达式（12）和剪切模量表达式（15）中都包括有切线模量Et，Et可采用邓肯-张模型的表达式：

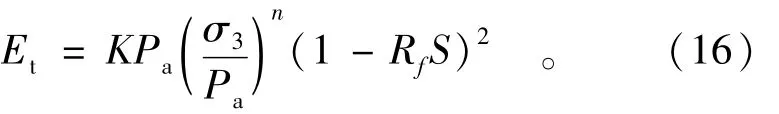
式中S为应力水平，表达式如下：

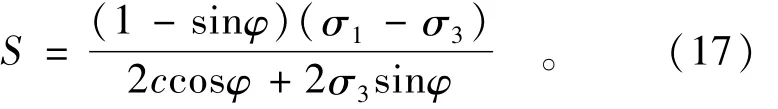
但大量试验表明，对于粗粒土，上式有必要修正。

图4为QP堆石料的切线模量Et与应力水平关系曲线。可以看出，式（16）反映的与实测的Et-S曲线形态差异较大，建议作如下修正：

式中包含7个参数，c，φ，K，n，Rf，α，β为试验确定的模型参数，邓肯-张模型作为其特例，α＝1，β＝2。不同的堆石料，α和β应该不同。

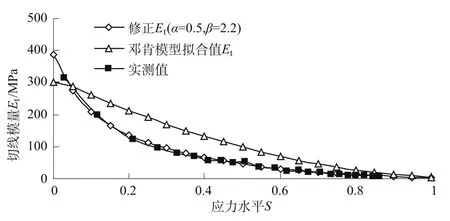
图4 QP堆石料切线模量E t比较（三轴σ3＝0.6 MPa）Fig.4 Comparison of tangent modulus E t of QP（triaxialσ3＝0.6 MPa）

3.6 模型参数和整理

在剪胀性模型的关系式（1）、（2）、（7）、（8）、（12）、（15）、（17）、（18）中共有 10个参数，c，φ，K，n，Rf，α，β，Kur，Kf，μ，其中 c和 φ为土的强度指标，由一组试验的不同围压下的峰值强度拟合确定。

K，n，Rf，α，β为切线模量参数，其中 K和 n由一组试验的初始切线模量拟合确定，Rf，α，β由切线模量Et与应力水平实测曲线（如图4）试算法确定，α和β体现曲线的形态，Rf反映高应力水平时Et的大小。

Kur与n联合确定土的弹性模量，可由一组退荷再加荷试验得到的弹性模量拟合确定，当未进行退荷再加荷试验时，也可由三轴体变曲线试算法确定。

Kf为土的剪胀性指标，先根据弹性模量计算试验应力条件下的弹性应变，由总应变扣除弹性应变得到剪胀应变，从而由式9计算Kf，也可由体变曲线试算法确定，Kf大小反映一组体变曲线的张开程度和体变曲线的形态。

μ为土的弹性泊松比，是虎克定律参数，反映土的弹性应变与应力间的关系。可由平面应变试验的中主应力σ2与σ1按下式确定：

模型中取其平均值作为其参数。

4 模型的试验验证

4.1 应力应变曲线计算

对于一个新的本构模型，最关心的问题是该模型对复杂应力条件的适用性，即所谓的模型合理性验证。本文采用的验证方式是：先采用常规三轴试验成果确定某一粗粒土的模型参数，再计算该粗粒土在平面应变试验条件下的应力应变曲线，并与平面应变试验结果进行比较。虽然该验证方式不够完善，但在一定程度上仍然能反映模型的合理性。

在平面应变状态下，应力和应变增量有下列换算关系：

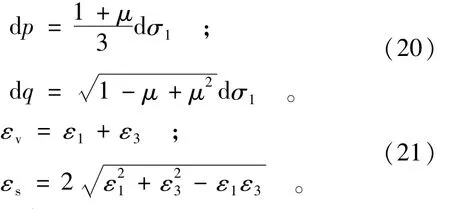
平面应变试验条件下的应力应变计算过程如下：

（1）对一小主应力σ3，循环增加大主应力dσ1；

（2）由式（7）、（8）、（12）、（15）、（17）、（18）计算应力状态为σ3和σ1时的变形模量Kp，Kq，G；

（3）由式（20）计算 d p和 d q；

（4）由式（1）、（2）计算应变增量 dεv和 dεs，及应变 εv和 εs；

（5）由式（21）计算应变 ε1；

（6）对不同小主应力σ3，重复上述过程，即可求得一组平面应变试验拟合曲线。

4.2 应力应变关系比较

2种堆石料的剪胀性模型拟合曲线如图2、图3所示，模型参数如表1。在平面应变试验曲线拟合中，为考虑中主应力影响，宜由下式等效应力σ0代替式（9）中的小主应力σ3：

其中 σ2由式（19）计算，对于三轴试验，σ0＝σ3。

从图2、图3和表1可以看出，剪胀性模型能够很好地模拟堆石料不同加载过程的应力应变关系，对于同一种堆石料，三轴试验和平面应变试验的模型参数除强度指标外，其它参数完全一致。

平面应变试验得到的堆石料强度比三轴试验高，在不少关于平面应变试验的文献中均可以看到同样结论，应该说这个结论具有普遍性。这种差别是由试样形状不同引起的，还是由中主应力引起的，需要试验进一步证明，可能2种因素都影响平面应变试验与三轴试验强度的差异。

初步研究表明，本文提出的剪胀性模型是一个具有实用性的本构模型。因此，可以认为，由三轴试验得到的3参量表达式（7）、（12）、（15）可推广到复杂应力状态中计算。

4.3 泊松比的讨论

假定土体应变分为弹性应变和剪胀应变，泊松比作为虎克定律的参数，反映土的弹性应变与应力间的关系，因此，泊松比可由平面应变试验的中主应力σ2与σ1按式（19）确定，为叙述的方便，称之为弹性泊松比。两种堆石料的弹性泊松比如图5所示，其大小约为0.1～0.3，与应力状态的关系不明显。其中，MS堆石料的弹性泊松比随应力水平增大而增大，QP堆石料的弹性泊松比随应力水平先增大而后减小。故模型中取其平均值作为其参数。

在一般的非线性弹性模型中，假定土体的应力应变关系完全服从虎克定律，因此，可由试验应变间的关系求得泊松比，为叙述方便，暂且称之为综合泊松比，计算式如下。令 A＝dεv／dε1

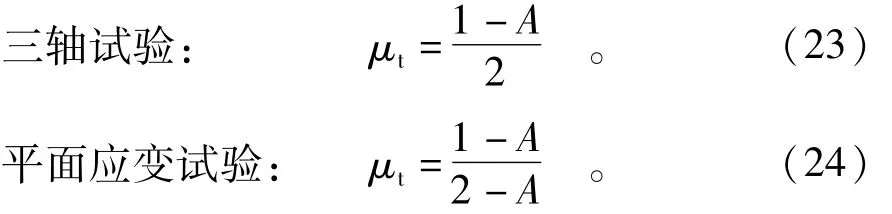
MS堆石料三轴试验和平面应变试验的综合泊松比如图6所示。

比较图6（a）、图 6（b），同一堆石料，由不同试验得到的综合泊松比相差较大，三轴试验为0.08～0.74，平面应变试验为0.26～0.58，综合泊松比常常出现大于0.5的现象。比较图 5（a）、图 6（b），对于同一堆石料，由同一组平面应变试验得到的两种泊松比也相差较大，由应力关系得到弹性泊松比为0.10～0.30，由应变关系得到综合泊松比为0.26～0.58。这些成果只能说明一点，粗粒土的应力应变关系不完全服从广义虎克定律。剪胀模型更好地反映了粒土的应力应变关系。

表1 模型参数Table 1 Parameters of the model

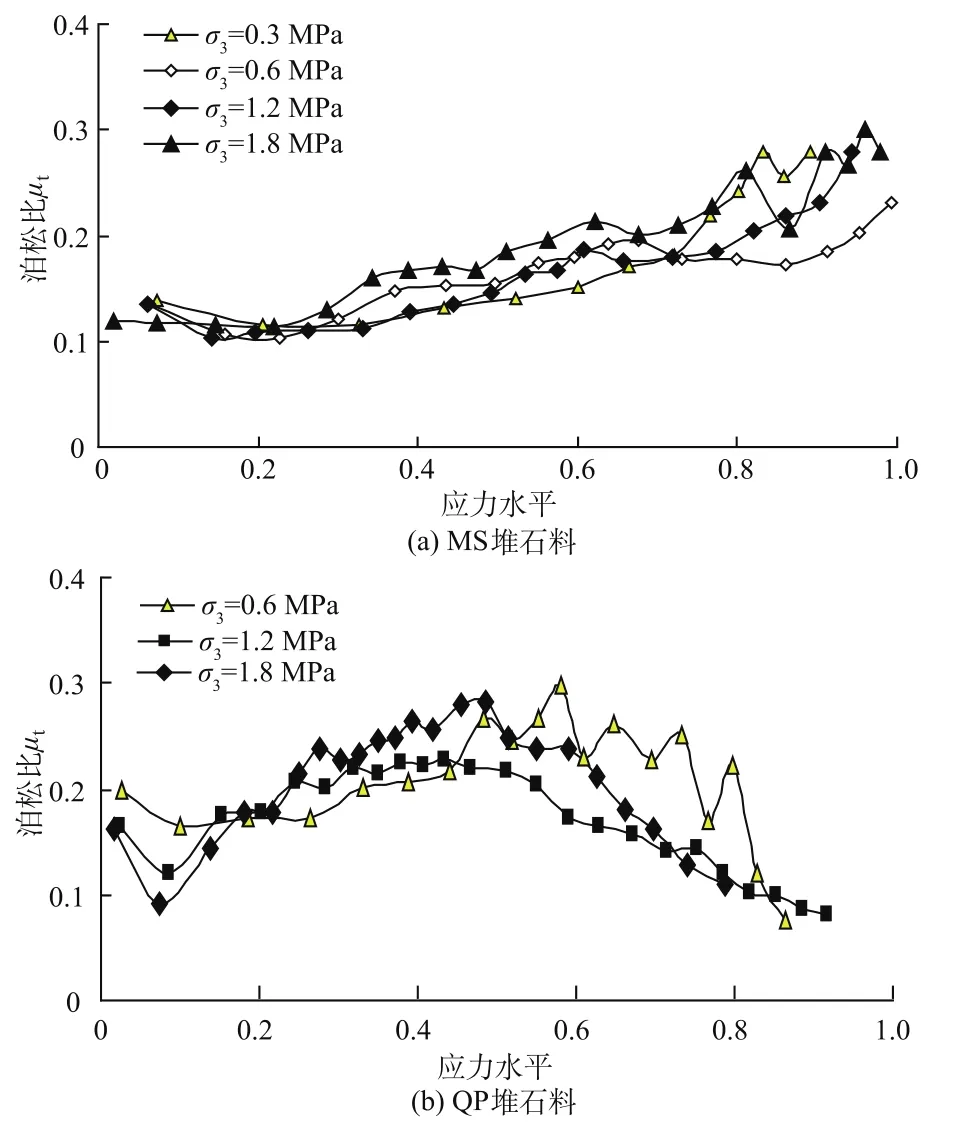
图5 平面应变试验实测泊松比Fig.5 The measured Poisson’s ratio of plane strain test

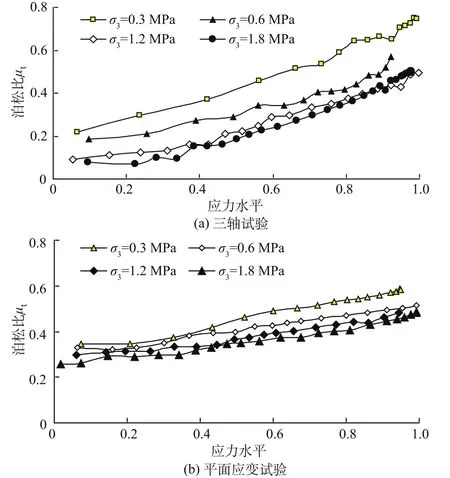
图6 MS堆石料综合泊松比Fig.6 The composite Poisson’s ratio of MScoarse-grained soils

5 结 论

岩土工程实践表明，一种实用性本构模型应该是能突出土的主要特性，力学概念简单，参数物理意义明确且不同土体的参数具有可比性。

本文根据粗粒土试验得到的应力应变间的规律性，假设土体应变分为弹性应变和剪胀应变，弹性应变与应力间服从广义虎克定律，剪胀应变服从Rowe剪胀方程，完整地建立了3参量Kp，Kq，G与应力关系式。2个堆石料的三轴和平面应变试验成果表明，该剪胀性模型能够很好地模拟堆石料三轴试验和平面应变试验的应力应变关系，且同一堆石料不同试验的模型参数有很好的一致性。目前，正着手将该模型编入有限元软件，并进行有关堆石坝的数值分析，期望得到工程的进一步验证。当然，更期望得到同行们的指证。

［1］ 程展林，姜景山，丁红顺，等.粗粒土非线性剪胀模型研究［J］.岩土工程学报，2010，32（3）：331－337.（CHENG Zhan-lin，JIANG Jing-shan，DING Hong-shun，et al.Nonlinear Dilatant Model for Coarse-Grained Soils［J］. Chinese Journal of Geotechnical Engineering，2010，32（3）：331－337.（in Chinese））

［2］ 曾以宁，屈智炯.土的非线性模型——K-G模型研究［C］∥土的抗剪强度与本构关系学术讨论会论文集.湖北老河口，1985：213－224.（ZENG Yi-ning，QU Zhijiong.Study on K-G Nonlinear Model［C］∥Proceedings of Symposium on Soil Shear Strength and Constitutive Relation.Hubei，Laohekou，1985：213－212.（in Chinese））

［3］ 殷建华，袁建新.土的非线性剪胀应力应变模型［C］∥土的抗剪强度与本构关系学术讨论会论文集.湖北老河口，1985：204－212.（YIN Jian-hua，YUAN Jian-xin.Nonlinear Dilitancy Stress Strain Model［C］∥Proceedings of Symposium on Soil Shear Strength and Constitutive Relation.Hubei，Laohekou，1985：204－212.（in Chinese））

［4］ 高莲士，赵红庆，张丙印.堆石料复杂应力路径试验及非线性K-G模型研究［C］∥国际高土石坝学术研讨会论文集.1993：110－117.（GAO Lian-shi，ZHAO Hong-qing，ZHANG Bing-yin.Complex Stress Path Test on Rockfill Materials and Study on K-G Nonlinear Model［C］∥Proceedings of the International Conference on High Earth-Rock Dam.1993：110－117.（in Chinese））

［5］ 姜景山，刘汉龙，程展林，等.密度和围压对粗粒土力学性质的影响［J］.长江科学院院报，2008，26（8）：46－50.（JIANG Jing-shan，LIU Han-long，CHENG Zhanlin，et al.Influences of Density and Confining Pressure on Mechanical Properties for Coarse-Grained Soils［J］.Journal of Yangtze River Scientific Research Institute，2008，26（8）：46－50.（in Chinese））［6］ 程展林，丁红顺，吴良平.粗粒土试验研究［J］.岩土工程学报，2007，29（8）：1151－1158.（CHENG Zhan-lin，DING Hong-shun，WU Liang-ping.Experimental Study on Mechanical Behaviour of Granular Material［J］.Chinese Journal of Geotechnical Engineering，2007，29（8）：1151－1158.（in Chinese））

［7］ 沈珠江.理论土力学［M］.北京：中国水利水电出版社，2000.（SHEN Zhu-jiang.Theoretical Soil Mechanics［M］.Beijing：China Water Power Press，2000.（in Chinese） ）

Further Discussion on Dilatancy Model for Coarse-Grained Soils

CHENG Zhan-lin1，CHEN Ou1，2，ZUO Yong-zhen1，DING Hong-shun1
（1.Key Laboratory of Geotechnical Mechanics and Engineering of MWR，Yangtze River Scientific Research Institute，Wuhan 430010，China；2.College of Water Conservancy and Hydropower Engineering，Hohai University，Nanjing 210098，China）

The test results of large triaxial test and plane strain test for two kinds of coarse-grained soils are firstly described.Soil strain is assumed as two parts composed of elastic strain and dilatancy strain.The relationship of elastic strain and stress is supposed to obey generalized Hooke’s law；while the dilatancy strain obeys Rowe dilatancy law，and the elastic Poisson’s ratio is assumed as constant.Based on these assumptions，the relationship between stress and three parameters including volumetric strain module Kp，dilatant module Kq，and shear module G is established，and a new nonlinear dilatancy model which is simple and practical with clear physical concept is preliminarily proposed.Subsequently，the collation method of the model parameters is given，and finally the mechanical significance of Poisson’s ratio of the general nonlinear elastic model is demonstrated.The tests indicate that the model can well simulate the stress-strain curve for different coarse-grained materials.As for the same coarse-grained soils，the model parameters from the triaxial test and plane strain test are consistent except for the strength index.Model parameters for two kinds of coarse-grained soils are also offered.

stress-strain relationship；constitutive model；plane strain test；dilatancy；coarse-grained soils；earth and rockfill dam

TU432

A

1001－5485（2011）06－0039－06

2010-08-13

国家自然科学基金委员会、二滩水电开发有限责任公司雅砻江水电开发联合研究基金项目（50639050）

程展林（1963-），男，湖北武穴人，教授级高级工程师，主要从事土力学研究，（电话）027-82926043（电子信箱）chengzl＠mail.crsri.cn。

（编辑：姜小兰）