大坝变形度的不等维加权动态GM（1，1）预测模型

崔冬冬，陈建康，吴震宇，程黎明

大坝变形度的不等维加权动态GM（1，1）预测模型

崔冬冬，陈建康，吴震宇，程黎明

（四川大学水利水电学院，成都 610065）

针对灰色GM（1，1）模型预测结果易受模型中以前测得的陈旧数据的干扰，及等维动态GM（1，1）受缚于维数选择的情况，给出了不等维加权动态GM（1，1）模型的基本内容及建模过程，模型中计算出多种维数的GM（1，1）模型的预测值，并且通过萨函数加权法和BP神经网络计算出每种维数的权值，通过加权获得最终预测值。并且成功地将不等维加权动态GM（1，1）模型应用于大坝变形度的预测预报。实践证明，不等维加权动态GM（1，1）模型由于考虑了维数对模型结果的影响，而且及时地更新数据，提高了灰区间的白色度，预测效果比传统的GM（1，1）模型和等维动态GM（1，1）模型效果好。

GM（1，1）模型；等维动态GM（1，1）；不等维加权动态GM（1，1）模型；权值；BP神经网络；萨函数

GM（1，1）模型长期预测的有效性明显受系统时间序列长短及数据变化的影响。如果系统建模选用的数据序列太短，则难以建立长期的预测模型；数据序列过长，系统受干扰的成分多，不稳定因素大，易使模型精度降低。为此，有些学者在进行GM（1，1）预测时不断地加入最新所测的数据，去除以前测得的陈旧数据，并加入等维的约束条件，采用等维动态预测模型来弥补现有灰色模型的不足［1］。但是应该指出，在GM（1，1）建模过程中，如果所选维数不当，矩阵及其逆矩阵会出现病态［2］，导致参数失真。有些学者专门研究过灰色理论的最佳维数问题，认为最佳维数与数据序列的特点有关系，不能一概而论。但可以通过数值试验来确定一个比较合适的最佳维数区。为了弥补这种不足，本文建立了不等维加权动态GM（1，1）模型。

1 GM（1，1）建模理论

灰色建模的设计思想［3］：原始数据序列经过一次累加后，形成一个递增数列，这个新数列数据点的连线接近于指数函数曲线，累加的次数越多，形成的数据点的连线也就越接近某个指数函数。那么根据这个指数函数可以外推到下1个（即第1个预测期）累加和，后经过累减还原得到原序列预测值。下面是 GM（1，1）建模过程［4］的具体步骤。

设大坝监测系统输出序列为 x（0）＝｛x（0）（1），x（0）（2），…，x（0）（k），…｝。以序列的前 n项作为系统的零时刻序列，构建零时刻系统的灰色模型，n为时刻序列长度。零时刻系统输出序列为x（0）0＝｛x（0）0（1），x（0）0（2），…，x（0）0（n）｝＝｛x（0）（1），x（0）（2），…，x（0）（n）｝，则：

（1）一次累加生成（1－Accumulated Generating Operation，1－AGO）。

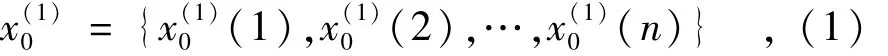
（2）求出均值序列。

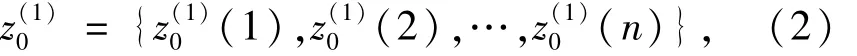
（3）求中间参数。

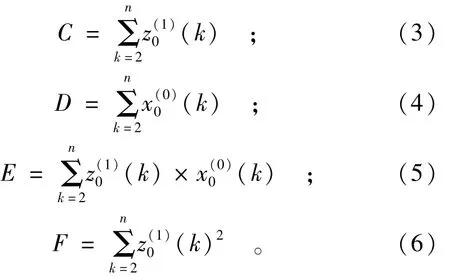
（4）计算发展系数和灰作用量。

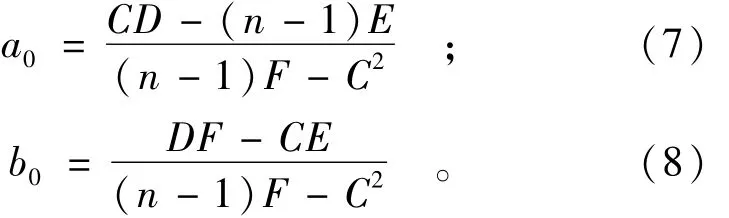
系统灰色微分方程为

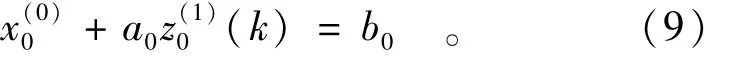
系统微分方程的白化方程为

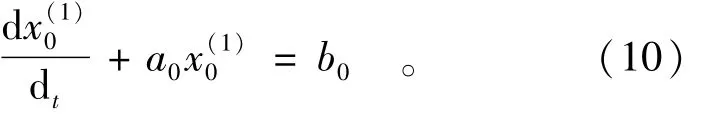
其灰色微分方程的时间相应序列为

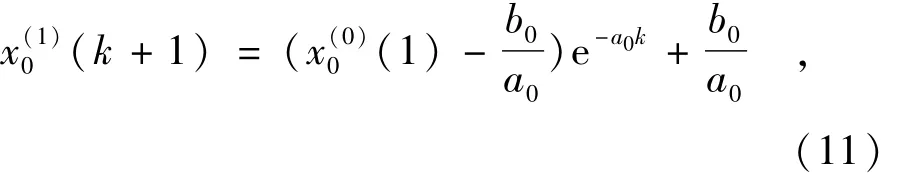
式中 k＝1，2，…，n－1。

累加公式反推如下：

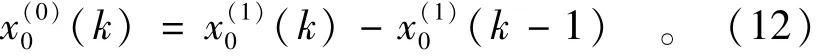
式中 k＝2，3，…，n。

此公式不仅可以建模，而且可以预测。

2 萨函数加权法

2.1 萨函数加权法

实测值为 x，其有 d个预测值 x〈1〉，x〈2〉，…，x〈d〉。每个预测值的偏差为

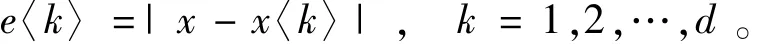
利用SPSS统计软件，对每个预测值的偏差进行分析，发现其相关度的系数值呈现出1种类似于萨函数 Sa（x）＝sin x／x的曲线规律，即测值偏差越小，对准确值的预测越准确；也可以认为偏差越小，对预测做的贡献越大。依据该规律将原有的预测值计算方法进行改进，引入加权平均的思想。因各个预测值在预测数据的计算中所占的比例不同，所以选取不同的权值系数进行预测运算。则每个预测值的权值

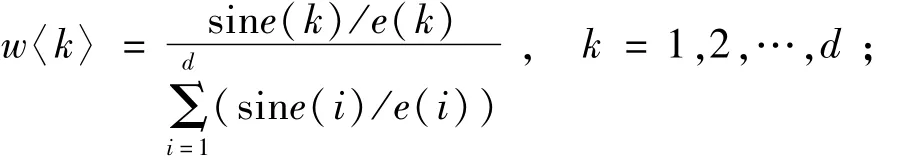
2.2 神经网络在权值估测中的应用

假设某时刻实测值未知，该时刻有d个预测值x〈1〉，x〈2〉，…，x〈d〉。不可能按照上面的方法得到每个预测值的权值，所以我们必须对预测值的权值进行估计。本文选取典型的三层前馈型BP（Back Propagation）网络模型［5］对预测值权值进行估计。BP神经网络是指在具有非线性传递函数神经元构成的神经网络中采用误差反向传播算法作为其学习算法的前馈网络。通常由输入层、隐含层和输出层构成。BP算法是一类有教师的学习算法，主要用于网络权值和阈值的学习修正。权值预测的具体实现步骤如下。

（1）初始化：初始化所有的网络权值为最小随机数。

（2）给出学习样本：找出预测时刻之前的m个数据，因为此m个数据实测值是已知的，所以可用上面的方法分别得出其预测权值，每个实测值都对应d个不等维GM（1，1）的预测值，每个预测值都有一个预测权值，把每个数据的所有预测模型的维数输入神经网络作为输入，每个数据的所有预测权值作为输出进行训练。

（3）计算实际输出：计算隐含层和输出层各神经元输出。隐含层传递函数采用tansig，输出层传递函数采用purelin。

（4）计算输出误差（采用均方误差）。

（5）调整输出层网络权值系数。

（6）调整隐含层网络权值系数。

（7）判断学习状态：如误差满足要求，则学习过程结束，否则返回第3步继续学习。

（8）输入所有模型维数进行仿真，把神经网络的输出作为当前时刻的权值。

其中节点作用激活函数f（u）采用Sigmoid型，即 f（u）＝［1＋exp（－（u＋θ））］－1。为提高网络熟练速度，对样本进行规范化处理，变换到［0，1］之间。设置最大学习次数1 000次，学习率0.01，学习目标为误差平方和0.01，网络连接权的初始值为［0，1］上的随机数。

3 等维动态灰色预测模型［6］的建立

设原始数据列为x（0），进行一次累加运算生成x（1）后建立 GM（1，1）模型，由（11）和（12）式得n＋1时刻预测值 ＾x（0）（n＋1）。去掉 x（0）（1），加入灰数＾x（0）（n＋1），重新构成等维动态序列 x（0）＝（x（0）（2），x（0）（3），…，＾x（0）（n＋1））建立新的 GM（1，1）模型，通过新序列预测 n＋2时刻的 ＾x（0）（n＋2），… ，如此递补，逐个预测，称为等维灰数递补动态预测。

等维灰数递补动态预测由于加入的信息不是实测值，而是预测值，它可以淡化灰平面的灰度，但仍然是灰色的。科学的建模过程应该是，一旦获得n＋1时刻的实际观测数据（称为新息），便对原来的GM（1，1）模型进行一次改进。其方法是在序列 x（0）中，去掉 x（0）（1）加入 x（0）（n＋1），构成新的动态序列：x（0）＝（x（0）（2），x（0）（3），…，x（0）（n＋1））。由于等维新息模型实时引入的是新的观测值，因此真实反映了系统状态的变化，可以有效地提高预报精度。

4 不等维距离加权动态GM（1，1）模型的建立

随着时间的推移，会不断获得新的数据。设第T时刻从原始数列中依次取d组子数列，分别为x（T0）〈m〉，x（T0）〈m＋1〉，…，x（T0）〈m＋d－1〉，其中

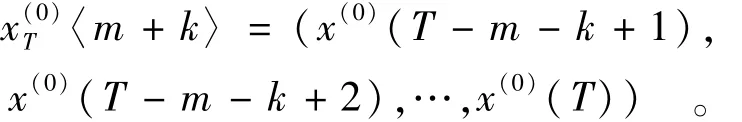
对x（0）T〈m〉，x（0）T〈m＋1〉，…，x（0）T〈m＋d－1〉分别进行一次累加得x（1）T〈m〉，x（1）T〈m＋1〉，…，x（1）T〈m＋d－1〉后建立 GM（1，m），GM（1，m＋1），…，GM（1，m＋d－1）模型，由（5）式得到 T＋1时刻的 d个预测值＾x（0）T（T＋1）〈m〉，＾x（0）T（T＋1）〈m＋1〉，…，（T＋1）〈m＋d－1〉。使用上面介绍的加权法对所有预测值加权，可得＾x（0）（T＋1）。然后去掉x（0）（n－m－k＋1），加入灰数＾x（0）（T＋1），重新构成不等维动态序列组，预测T＋2时刻＾x（0）（T＋2），…，如此递补，逐个预测，称这种方法为不等维加权灰数递补动态预测法。

同样，不等维加权灰数递补动态预测加入的信息不是实测值，而是预测值，比较合理的方法是，如果获得T＋1时刻的新息 ，便改进原来的GM（1，1）模型。改进的方法是在序列组中的每个子序列x（T0）〈m＋k〉用 x（0）（T＋1）替换 x（0）（n－m－k＋1），构成新的动态序列组，然后按照上面方法预测下一时刻的值。

5 不等维动态GM（1，1）模型的应用及成果分析

本文用C＃在.net平台下开发了等维动态GM（1，1）灰色模型和不等维加权动态 GM（1，1）模型。很多学者都对等维动态GM（1，1）灰色模型做了详细的研究，证明了等维动态GM（1，1）灰色模型比传统静态 GM（1，1）灰色模型更合理［6］，因此本文没有列出传统静态GM（1，1）灰色模型的结果。仅对某混凝土大坝的P08号测点水平位移分别建立了等维动态 GM（1，1）和不等维加权动态 GM（1，1）。表 1为此测点2008年1月至2009年4月之间的一组月平均数据。用这2种模型分别拟合2008年1月至2009年2月的数据，并给出2009年3月至2009年4月数据的预测值。其中拟合采用的是逐次加入新息的方法，预测采用的是灰数递补动态预测的方法。通过计算值与实际值的比较来检验模型精度。

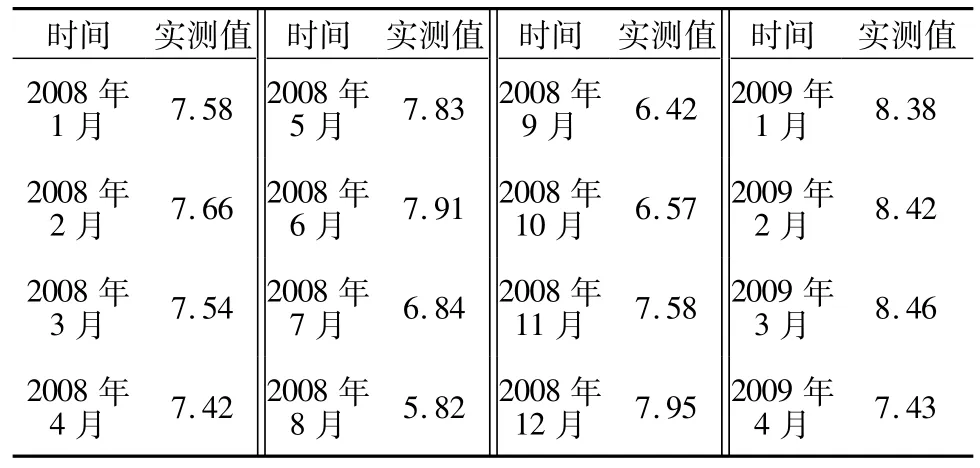
表1 水平位移测量序列Table 1 The measurement sequence of horizontal displacement

首先建立等维动态GM（1，1）灰色模型，选择维数为7，其建立方法和以往许多学者建立方法基本相同。然后建立不等维加权动态GM（1，1）模型，所谓“不等维加权”即为对维数不等的灰色GM（1，1）模型所得结果进行加权。首先选择维数，本文选择最大维数为7，最小维数为5，假设要拟合2008年7月的数据，就要有3组序列。其中维数为7的序列为2008年1月至2008年7月的数据，维数为6的序列为2008年2月至2008年7月的数据；维数为5的序列为2008年3月至2008年7月的数据。然后对这3组序列分别建立GM（1，1）模型，得到3组预测结果，可知2008年1月只有1个预测值，所以取此数据为其预测值，2008年2月有2个预测值，对这2个预测值进行萨函数加权法，往后每月都有3个预测值，对这3个预测值进行萨函数加权法。因为拟合采用的是逐次加入新息的方法，所以可以直接求出权值。其余各月的预测也是如此。表2和表3分别列出了等维动态GM（1，1）模型和不等维加权动态GM（1，1）模型的结果，由于是“动态”预测，而且等维动态GM（1，1）模型得维数为7，不等维加权动态GM（1，1）模型的最大维数也为7，所以每个模型共得到8组拟合值，每组拟合值有7个。表中同时列出了每组拟合值的平均残差。

数据估计的主要目的在于预测，因此本文对2009年3月至4月数据进行了试预测。即假设不知其实测值，用灰数递补动态预测的方法进行预测，然后与实测值进行比较。假设要预测2009年3月的数据，选2008年8月至2009年2月数据作为维数为7的序列；2008年9月至2009年2月数据作为维数为6的序列；2008年10月至2009年2月数据作为维数为5的序列。建立GM（1，1）模型分别对2009年3月数据进行预测，得到3个数据。因为实测值不知，所以不能直接用萨函数加权法，把前面拟合的维数作为输入，每个维数对应的权值作为输出进行BP神经网络训练，达到一定精度或训练了一定次数后，把本问题中的维数作为输入，输出即认为是本问题中的权值。对上面3个数据加权平均即得到2009年3月的预测值。把2009年3月的预测值加入序列就可对2009年4月的数据进行预测。表4列出了等维动态GM（1，1）模型和不等维加权动态GM（1，1）模型的预测值，也给出了每个预测值的残差。

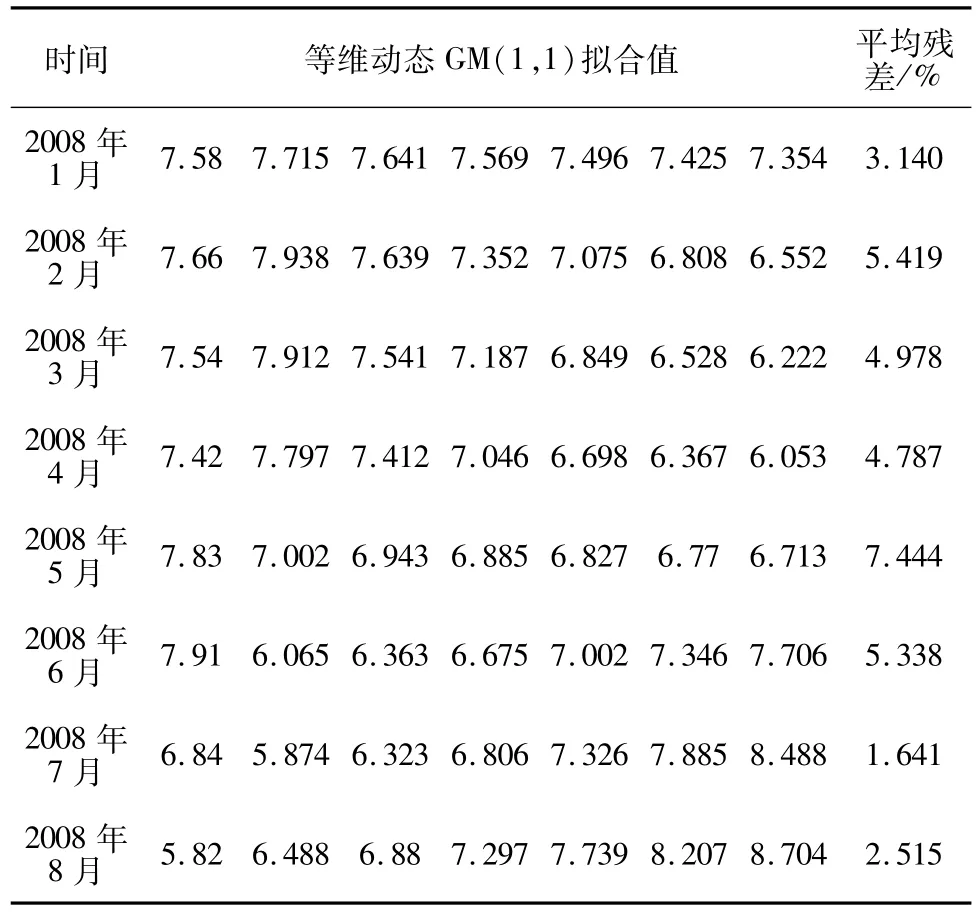
表2 等维动态GM（1，1）模型拟合值及平均残差Table 2 Fitted values and average residuals of one-dimensional dynamic GM（1，1）model

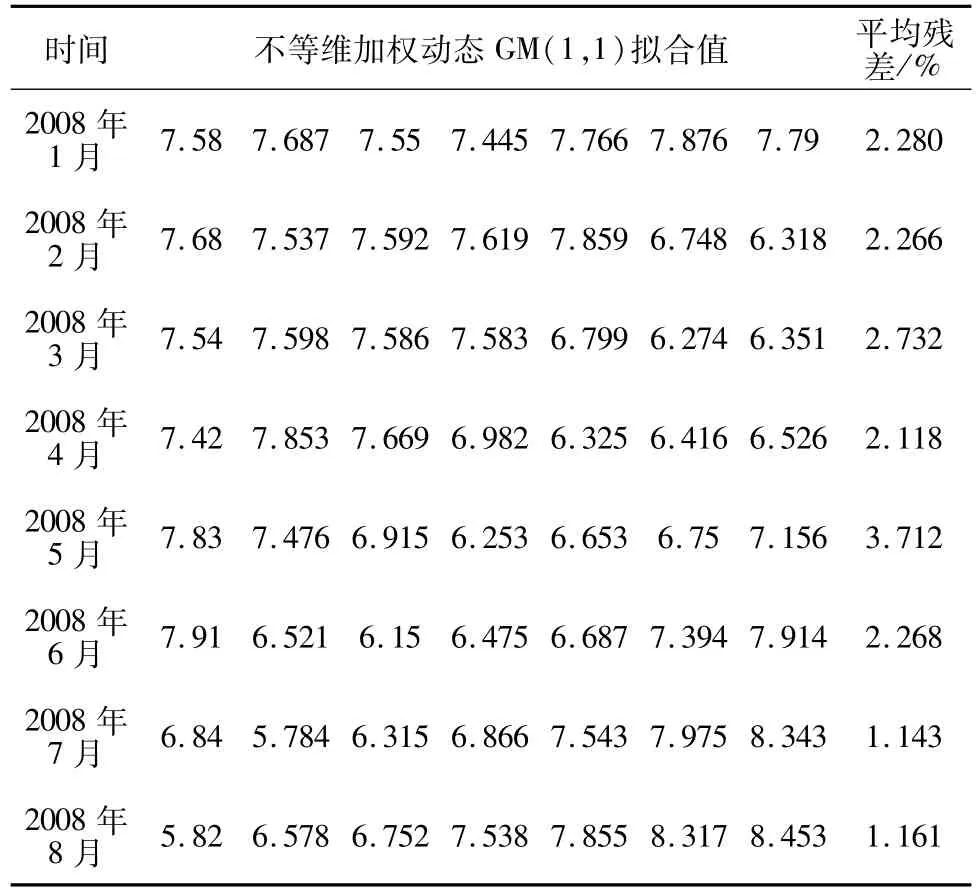
表3 不等维加权动态GM（1，1）模型拟合值及平均残差Table 3 Fitted values and average residuals of MDWD-GM（1，1）model

对比表2和表3的数据可得，不等维加权动态GM（1，1）模型的拟合效果明显高于等维动态GM（1，1）模型。通过表4的数据也可以得出，不等维加权动态GM（1，1）模型的预测精度也好于等维动态GM（1，1）模型。因此可以认为不等维加权动态GM（1，1）模型总体上优于等维动态 GM（1，1）模型，具有更高的利用价值。

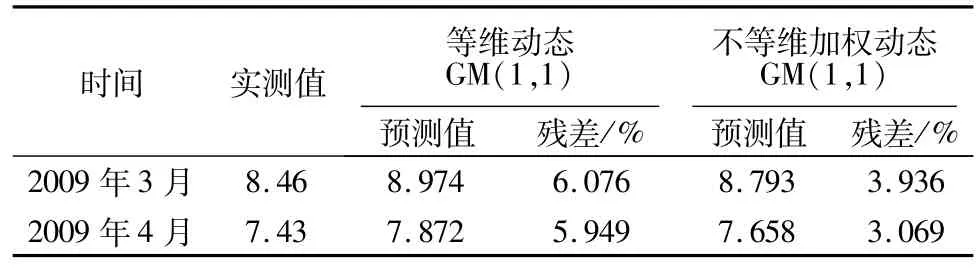
表4 等维动态GM（1，1）与不等维加权动态GM（1，1）模型预测值及相对残差Table 4 Predictive values and relative residuals of one-dimensional dynamic GM（1，1）model and MDWD-GM（1，1）model

6 结 论

本文采用萨函数加权法和BP神经网络建立了不等维加权动态GM（1，1）模型。该模型将大坝监测数据看作是灰色过程，动态的添加新息，以减少其它不相关信息的干扰，而且考虑了维数对灰色模型的影响，对不同维数的灰色模型预测结果加权，减少了维数对预测精度的影响。通过对实测数据进行拟合和预测，可以得出此模型可以很好地拟合大坝监测数据，并给出比较准确的预测值的结论。不等维加权动态GM（1，1）模型在大坝监测系统中具有更高的利用价值。

［1］ 傅 立.灰色系统理论及其应用［M］.北京：科学技术文献出版社，1992：58－81.（FU Li.Grey System Theory and Its Application［M］.Beijing：Science and Technology Document Press，1992：58－81.（in Chinese））

［2］ 尹 晖.时空变形分析与预报的理论与方法［M］.北京：测绘出版社，2002：52－57.（YIN Hui.Theory and Method of Space Deformation Analysis and Prediction［M］.Beijing：Surveying and Mapping Press，2002：52－57.（in Chinese））

［3］ 邓聚龙.灰色系统理论教程［M］.武汉：华中理工大学出版社，1990：14－83，326－328.（DENG Ju-long.Theory of Grey System［M］.Wuhan：Huazhong University of Science and Technology Press，1990：14－83，326－328.（in Chinese））

［4］ 邓聚龙.灰色系统基本方法［M］.武汉：华中理工大学出版社，1987：96－164.（DENG Ju-long.Basic Methods of Grey System［M］.Wuhan：Huazhong University of Science and Technology Press，1987：96－164.（in Chinese））

［5］ 李少华，董增川.BP神经网络模型应用于大坝原型观测研究［J］.水利与建筑工程学报，2004，2（2）：31－33.（LI Shao-hua，DONGZeng-chuan.Application of BP Neural Network Model in Dam Deformation Monitoring［J］.Journal of Water Resources and Architectural Engineering，2004，2（2）：31－33.（in Chinese））

［6］ 李宗坤，郑晶星.GM（1，1）等维新息模型在土石坝沉降预测中的应用［J］.水利水电技术，2003，34（7）：74－75.（LI Zong-kun，ZHENG Jing-xing.The Dynamic GM（1，1）Model Applied in the Prediction of Settlement of Earth Dam［J］.Water Resources and Hydropower Engineering，2003，34（7）：74－75.（in Chinese） ）

Multidimensional Weighted Dynamic GM（1，1）Model Applied in the Prediction of Dam Deformation Degree

CUI Dong-dong，CHEN Jian-kang，WU Zhen-yu，CHENG Li-ming
（College of Water Resource and Hydropower，Sichuan University，Chengdu 610065，China）

The prediction result of GM（1，1）grey model is subject to be disturbed by outdated information previously measured in the system，while one-dimensional dynamic GM（1，1）model is restrained by the selection of the dimension.To overcome these problems，this paper studies the content and the modeling of Multidimensional Weighted Dynamic GM（1，1）model（MDWD-GM（1，1）model）in detail.Based on the prediction results of all the dimensions calculated by this model，the weight value of each dimension is obtained by Sa function weighting method and BPneural network，then the final predictive value is obtained by weighting.Moreover，the MDWD-GM（1，1）model has been applied to the dam monitoring system and the application manifests that it offers better prediction results than traditional GM（1，1）model and one-dimensional dynamic GM（1，1）model as it takes the effect of different dimensions into account and increases the white degree of the grey range by updating the data in time.

GM（1，1）model；one-dimensional dynamic GM（1，1）model；multidimensional weighted dynamic GM（1，1）model；weight；BP neural network；the Sa function

TV698

A

1001－5485（2011）06－0005－05

2010-09-06；

2010-10-19

崔冬冬（1987-），男，安徽阜阳人，硕士研究生，主要从事水工结构工程及基础工程研究，（电话）15208215241（电子信箱）631505116＠qq.com。

（编辑：曾小汉）