用微进化算法反演岩石蠕变模型非定常参数

彭汝发，许小健

用微进化算法反演岩石蠕变模型非定常参数

彭汝发，许小健

（芜湖市勘察测绘设计研究院，安徽芜湖 241000）

岩石蠕变模型的参数较多，为得到参数的全局最优解，应用微进化算法（Microevolution Algorithm，MA）对岩石蠕变模型非定常参数进行了反演分析。算法以实测蠕变值与理论计算值之间的最小二乘误差为优化准则函数，直接反演计算蠕变模型参数。计算结果表明，微进化算法可最大限度地利用所有试验数据，避免传统优化算法初始参数选取的困难，且算法简单有效，计算精度高于混沌粒子群优化算法。该方法也可推广应用于其它蠕变模型的参数反演，具有较高的工程应用价值。

岩石蠕变模型；非定常参数反演；微进化算法

1 概 述

岩石的蠕变研究对于合理评价岩体的长期稳定性，即岩石力学行为的时间效应具有重要意义。岩石蠕变研究一般是从试验出发获取有关数据，然后构建岩石蠕变的本构模型并确定相应的模型参数。因此，根据蠕变试验资料，如何正确确定岩石蠕变模型参数是岩石蠕变研究领域的关键课题之一。目前，确定岩石蠕变模型参数的方法主要有最小二乘法［1］、多项式回归法［2］、流变曲线分解法［3］、复合形优化法［4］、模式搜索算法［5］等。但岩石蠕变模型的参数众多，为得到问题的全局最优解，须尝试应用新的优化算法。近些年来，随着优化计算技术的发展，人工神经网络［6］、遗传算法（Genetic Algorithm，GA）［7］、扩展卡尔曼滤波技术［8］、粒子群优化（Particle Swarm Optimization，PSO）算法［9］等逐渐在岩石蠕变模型参数确定中得到了应用，为解决问题提供了一种新的思路。

基于算法简单性和寻优精度方面的考虑，本文给出了岩石蠕变模型非定常参数智能反演的一种新算法——微进化算法 （Microevolution Algorithm，MA），并利用页岩的蠕变试验数据进行了参数反演分析。计算结果表明，微进化算法作为蠕变模型参数反演的新方法是可行有效的，且算法计算精度高于混沌粒子群优化算法，具有较高的工程应用价值。

2 微进化算法基本原理

微进化算法，是受人类社会发展进程中人类趋同和趋异学习行为过程的启发构造出来的。它所采用的基本搜索策略是：群体中的每一个个体向群体中的优秀个体学习，利用优秀个体积累的经验知识来改变自身，使自身得以处于不断运动之中。具体来说，MA基于实数编码，采用群体社会学习机制，对种群中的每个个体i，以其自身所处历史最优位置为基础，以群体最佳位置与当前个体i的矢量差异为信息参照，进行动态随机搜索，以实现种群的进化。

为便于描述，设 Xi＝（xi1，xi2，…，xiD）为个体 i＝1，2，…，NP的 D维矢量，每个 Xi代表一个潜在的解；设Xpbesti为个体i迄今为止搜索到的最优状态、Xgbest为整个群体中的所有个体迄今为止搜索到的最优位置状态。这样，在每一次的迭代搜索中，以式（1）更新各个体所处状态：

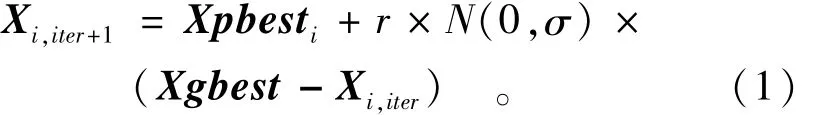
式中：iter为迭代次数；r为0～1之间的正实数，一般为了使用方便，可令 r∈U（0，1）；N（0，σ）为正态分布随机数，其中 σ∈（0.5，2.5）。

分析式（1）可知，当 Ni（0，σ）＞0时，群体中的各个体 i以矢量差（Xgbest－Xi，iter）为方向趋同；当Ni（0，σ）＜0时，各个体以矢量差（Xgbest－Xi，iter）的反方向趋异。可见，式（1）将趋同与趋异有机地结合了起来，以实现局部的开采与全局的探索进化功能。算法实现步骤如下。

步骤1（初始化）：令 iter＝0，采用实数编码，在可行域空间随机初始化种群 Xiter＝（X1，iter，X2，iter，…，Xi，iter，…，XNP，iter）T，若搜索空间为 D维，则每个个体Xi，iter中包含了 D个变量，即 Xi，iter＝（xi1，iter，xi2，iter，…，xij，iter，…，xiD，iter），j＝1，2，…，D。

步骤2（种群评价）：评价种群中每一个个体，求出每一个个体到目前为止找到的最优解，记为Xpbesti，i＝1，2，…，NP；将所有 Xpbesti中目标函数值最 优 的 个 体 记 为 Xgbest，即 Xgbest＝min｛Xpbest1，Xpbest2，…，Xgbesti，…XpbestNP｝。

步骤3（种群演化）：执行如下操作，产生第iter＋1代种群 Xiter＋1。

步骤4（终止检验）：①判断算法循环执行次数是否达到最大进化代数ITERMAX；②判断最优目标函数值f（Xgbest）是否达到预设精度VTR。若满足终止条件其中之一，则结束算法，输出Xgbest及其目标函数值，否则，转入步骤2直至满足终止条件。

由算法的实现步骤可见，微进化算法采用的基本策略是：①采用实数编码；②使用固定规模的种群NP；③采用贪婪的种群更新策略，即用NP个新个体Xi，iter＋1完全替换 NP个旧个体 Xi，iter；④采用精英保留策略，即更新个体自身所处历史最优状态Xpbesti和群体最佳状态Xgbest。

MA需要设置的算法控制参数较少，除算法的运行控制参数（ITERMAX、VTR）外，仅需设置群体数目NP和σ。过大的NP会影响算法的运算速度，经试验，对于一般问题，建议 NP取20～40左右；而σ∈（0.5，2.5），一般取 1即可获得较满意解。可见，与GA和PSO算法相比，MA控制参数的选择更为简单，这使得算法易于编程实现和便于用户使用。

3 微进化算法在岩石蠕变模型非定常参数反演中的应用

为探讨本文的微进化算法优化反演岩石蠕变模型参数的可行性，利用文献［10］中的页岩蠕变试验数据，采用标准线性体三元件模型，并引入非定常参数后进行反演分析。

对于标准线性体三元件模型，蠕变试验时，其本构方程为

在蠕变本构方程中引入非定常参数EK（t）＝p1＋p2ep3t，并令 ηK＝p4，EH＝p5，式（2）变为［9］

设式（3）等式左边和右边项分别记为fL和fR，则根据式（3），由 m对实测蠕变数据｛tl，εl｝（l＝1，2，…，m）可建立反演问题的优化准则函数为

式中，X＝（p1，p2，p3，p4，p5）为待反演参数。由于式（4）具有高度的非线性特征，传统优化方法如高斯-牛顿或麦夸特法等，对输入的模型参数初始值有一定的要求，若输入的参数值与参数的真实值偏离较大，可能造成迭代不收敛，而且也很难得到全局优化解。而本文微进化算法对模型是否线性、连续等没有限制，也不受优化变量数目的束缚，直接在优化准则函数的引导下进行全局自适应寻优，该方法简便、通用、适应性强。因此，现利用MA进行反演计算，步骤如下。

步骤1：初始化NP组待反演的蠕变参数Xi∈（p1，p2，p3，p4，p5），i＝1，…，NP，作为初始种群。

步骤2：将m组蠕变试验数据和初始化得NP组待反演的蠕变参数代入已建立的反演问题的优化准则函数式（4）中，计算得到相应应力水平下的最小二乘误差。

步骤3：评价各组待反演蠕变参数Xi，更新Xgbest。

步骤4：利用式（1）策略进行微进化寻优操作，并重复执行步骤3，直至满足微进化算法的终止条件，然后输出待反演蠕变参数的结果以达到最优化的目的。

根据上述蠕变参数的优化反演步骤，可反演计算得到页岩的蠕变模型非定常参数，如表1。为便于与文献［9］提出的混沌粒子群优化（Chaos Particle Swarm Optimization，CPSO）算法进行比较，表1中也列出了CPSO算法反演的参数结果。比较可见，在各应力水平作用下，MA与CPSO算法反演的参数p1，p5结果差别不大，而参数 p2，p3，p4差别较大，相差达一个数量级之多。由优化准则函数值min J结果可见，MA计算所得非定常参数的最小二乘误差远小于CPSO计算所得的最小二乘误差，MA可将优化准则函数值min J较少50%左右，这说明MA较CPSO算法在处理式（4）所示这种较为复杂的非线性模型时，具有更高的寻优精度。

为便于直观反映MA与CPSO算法反演不同应力水平各时刻的应变值，图1绘出了两种算法所得蠕变计算值与试验值结果。从图1可以看出，各应力水平下，MA计算所得理论反演变形曲线与试验变形曲线较为吻合，误差较小，说明本文提出的MA是有效可靠的；而在应力水平σc＝90 MPa，σc＝300 MPa时，CPSO算法计算所得的后期理论变形曲线偏离试验曲线相对较大。

表1 微进化算法与混沌粒子群算法反演结果的比较Table 1 Comparison between MA and CPSO inversion results

图1 试验数据及拟合曲线Fig.1 The test data and the fitting curves

4 结 论

（1）以实测蠕变值与理论计算值之间的最小二乘误差为优化准则函数，用微进化算法对岩石蠕变模型非定常参数进行优化反演，能最大限度地利用所有试验数据，且可避免传统优化算法初始参数选取的困难。算例计算结果表明，微进化算法不受初始选值的影响，计算精度高于混沌粒子群优化算法，具有较高的工程应用价值。

（2）本文虽以标准线性体三元件模型为例，进行了非定常参数的反演分析，但方法同样适用于其他蠕变模型，只需采用与模型对应的蠕变本构方程作为优化准则即可。

（3）微进化算法简单有效，且易于编程实现和便于用户使用。

［1］ 王宏贵，巍丽敏，赫晓光.根据长期单向压缩试验结果确定三维流变模型参数［J］.岩土工程学报，2006，28（5）：669－673.（WANG Hong-gui，WEI Li-min，HE Xiao-guang. Determination of Three-Dimensional Rheologic Parameters Based on Long Term Oedometer Test［J］.Chinese Journal of Geotechnical Engineering，2006，28（5）：669－673.（in Chinese））

［2］ 许宏发，陈新万.多项式回归间接求解岩石流变力学参数的方法［J］.有色金属，1994，46（4）：19－22.（XU Hong-fa，CHEN Xin-wan.Method to Find Indirect Solution of Rock Rheology’s Parameters with Polynomial Regression［J］.Nonferrous Metals，1994，46（4）：19－22.（in Chinese））

［3］ BOUKHAROV G N，CHANDA M W，BOUKHAROV N G.The Three Processes of Brittle Crystalline Rock Creep［J］.International Journal of Rock Mechanics，Mining Science and Geomechanics Abstract，1995，32（4）：325－335.

［4］ 李云鹏，王芝银，丁秀丽.岩体原位流变荷载试验的力学参数与模型反演［J］.实验力学，2005，20（2）：297－303.（LI Yun-peng，WANG Zhi-yin，DING Xiuli.Back Analysis of Mechanical Parameters and Model of Rheological In-situ Loading Test for Rock Mass［J］.Journal of Experimental Mechanics，2005，20（2）：297－303.（in Chinese））

［5］ 陈炳瑞，冯夏庭，丁秀丽，等.基于模式搜索的岩石流变模型参数识别［J］.岩石力学与工程学报，2005，24（2）：207－211.（CHEN Bing-rui，FENG Xia-ting，DING Xiu-li，et al.Rheological Model and Parameters I-dentification of Rock Based on Pattern Search and Least-Square Techniques［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（2）：207－211.（in Chinese））

［6］ 陈炳瑞，冯夏庭，丁秀丽，等.基于模式-遗传-神经网络的流变参数反演［J］.岩石力学与工程学报，2005，24（4）：553－558.（CHEN Bing-rui，FENG Xia-ting，DINGXiu-li，et al.Back Analysis on Rheological Parameters Based on Pattern-Genetic-Neural Network［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（4）：553－558.（in Chinese））

［7］ 刘 杰，王 媛.岩体流变参数反演的加速遗传算法［J］.大坝观测与土工测试，2001，25（6）：24－27.（LIU Jie，WANG Yuan.Back Analysis of Rock Mass Rheologic Parameters Based on Genetic Algorithm［J］.Dam Observation and Geotechnical Tests，2001，25（6）：24－27.（in Chinese））

［8］ 杨成祥，冯夏庭，陈炳瑞.基于扩展卡尔曼滤波的岩石流变模型参数识别［J］.岩石力学与工程学报，2007，26（4）：754－761.（YANG Cheng-xiang，FENG Xia-ting，CHEN Bing-rui. Parameter Identification of Rock Rheological Model Based on Extended Kalman Filter［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（4）：754－761.（in Chinese））

［9］ 丁志坤.岩石粘弹性性非定常蠕变方程的参数辨识［D］.济南：山东科技大学，2003.（DING Zhi-kun.Parameter Identification of Non-stationary Creep Equation of Rock.Jinan：Shandong University of Science and Technology，2003.（in Chinese））

［10］李志敬，朱珍德，周伟华.基于CPSO算法的岩石蠕变模型非定常参数反演分析［J］.河海大学学报（自然科学版），2008，36（3）：346－349.（LI Zhi-jing，ZHU Zhen-de，ZHOU Wei-hua.Back Analysis of Nonstationary Parameters of Rock Creep Model Based on Chaos Particle Swarm Optimization Algorithm［J］.Journal of Hohai University（Natural Sciences），2008，36（3）：346－349.（in Chinese） ）

Microevolution Algorithm for Inversion of Non-stationary Parameters in Rock Creep Model

PENG Ru-fa，XU Xiao-jian
（Wuhu Geotechnical and Survey Design Institute，Wuhu 241000，China）

Rock creep model generally contains several parameters.To obtain the global optimal solution of the parameters，Microevolution Algorithm（MA）was employed for the inversion of non-stationary parameters.In this paper，parameters of the creep model are directly inversed with the least square error between measured creep values and calculated creep values as the optimization criterion function.The computation results demonstrate that microevolution algorithm can maximize the use of all test data and avoid the difficulty of selecting initial parameters in traditional optimization algorithm.Moreover，microevolution algorithm is simple and effective，and offers higher accuracy than Chaos Particle Swarm Optimization（CPSO）.In this sense，it can be applied to the inversion of parameters in other creep models and has high application value for engineering.

rock creep model；inversion of non-stationary parameter；microevolution algorithm

TU425

A

1001－5485（2011）06－0050－05

2010-07-21

彭汝发（1964-），男，安徽桐城人，高级工程师，主要从事岩土工程勘察设计方面的工作，（电话）0553-3827968（电子信箱）907137382＠qq.com

（编辑：赵卫兵）