顾及不确定度的数字水深模型内插方法
张立华,贾帅东,吴 超,殷晓冬
海军大连舰艇学院海洋测绘科学与工程系,辽宁大连116018
顾及不确定度的数字水深模型内插方法
张立华,贾帅东,吴 超,殷晓冬
海军大连舰艇学院海洋测绘科学与工程系,辽宁大连116018
提出一种顾及不确定度的数字水深模型(DDM)内插方法。计算数据来源不同的水深不确定度,构建水深数据权重配赋中加入不确定度的数据内插模型,实现水深内插点的不确定度估计。试验证明,所提方法提高了DDM的构建质量,并可评估内插水深的不确定度。
数字水深模型;不确定度;内插
1 引 言
高质量的数字水深模型(digital depth model, DDM)构建,在舰船海上航行、海洋工程建设、海底勘探、军事活动等应用领域都具有重要意义[1]。长期以来,在海道测量和海图制图界,认为原始观测水深的准确度和可靠性高,出于舰船航行安全起见,一律强调保留原始水深以及采用保守的“取浅”规则,所以数据处理中,对内插水深鲜有应用[2-3]。但事实上,在不需要保守水深而更需要真实地形的领域(如海洋水文、海洋声学、海底勘探、海洋考古等),由于格网化水深具有数据结构及管理表达上的优越性,对内插水深也存在需求[1]。另外,在港口水深测量中,某些用户为了读图方便,也明确要求提供格网化内插水深图[4]。特别是近年来,随着多波束测深的应用以及测深定位精度的不断提高,格网化水深内插开始广泛应用[1,5-6]。然而,在当前的水深内插方法中,通常将水深数据等同精度处理,而未考虑水深数据来源多样性而导致不等精度的客观事实。在不同区域、不同测线之间的交界及其附近区域,由于测量时间不同、使用仪器不同、采集方式各异,水深数据的精度存在不同;在海图上,经常采用测量年代、来源不同的数据区域块,在这些区域相接及其邻近区域,导致水深数据质量存在诸多差异。而当前进行水深内插时,未有效考虑不同数据来源在数据质量上的这种差异,将影响DDM内插的质量。同时当前方法无法对内插后的水深精度指标进行质量评估,这使得难于对DDM内插方法进行合理性判断[1,4-6]。
不确定度表示在某一明确的置信度下,包含测量真值(关于某一给定的值)的区间[7],表示由于测量误差的存在而对被测量值不能确定的程度。一个完整的测量结果,不仅要给出测量值的大小,而且要给出测量不确定度,以表示测量结果的可信程度[5]。2008年新版的国际海道测量标准S-44(5版)明确要求,将不确定度作为水深值的精度指标与水深点信息一起存储[8]。近年来,有学者在阐述水深不确定度与传统水深精度表达之间的关系的基础上,突破长期以来水深测量成果仅以测点位置和水深值表达海底地形的现状,开始对单个水深进行不确定度的质量评定[1,8-9]。
因此,顾及不同源水深数据不确定度的差异,分析其对DDM构建的影响,并估计内插后水深及DDM的质量,具有现实意义。
2 顾及不确定度的DDM构建方法
2.1 水深不确定度计算
2.1.1 不确定度估计
不确定度估计的严密方法是:首先分析全误差Δδ中包含的随机误差和各种系统误差成分,计算Δδ的标准差σδ;其次确定Δδ的概率分布,根据概率分布的置信度,获得置信系数 kδ,即得其扩展不确定度[10]

可见扩展不确定度的确定关键在于概率分布和相应的置信度以及标准差σδ的获取。在国际海道测量标准(S-44)中,已假定测深数据服从正态分布,并要求置信度为95%,故在其不确定度的评定过程中,需详细分析误差源,给出具体的标准差,方能确定其不确定度的大小。
2.1.2 水平不确定度的计算
多波束测深由于测量载体受风、流和涌浪等各种干扰因素的影响,会产生横摇、纵摇、艏摇及载体升沉等运动,这些运动将使测深点归算问题转化为多维动态改正问题,其改正量将随测船航向变化和摇摆幅度大小而改变,具有明显的时变性,这就是海洋测量中的所谓动态偏心改正、动态位置传算以及动态时延改正问题[11],故多波束测深测点在水平方向上的标准差可表示为

式中,σ0为定位仪器的精度;σΔx和σΔy分别对应于前面三项改正综合的计算精度;σyv为声线改正在水平方向上的中误差。
对于单波束测深并未考虑上述动态改正,故其测点在水平方向上的标准差可简单表示为

因此σPosition可视为水平方向上的标准差,是一个二维数据,根据统计学知识,此时σPosition的置信水平为68%,需将其扩展至95%,以满足S-44规范的要求。根据σPosition服从正态分布的特性与其相应的置信水平,水平不确定度σH可表示为[7]

2.1.3 垂直不确定度的计算
针对多波束测深系统在垂直方向上误差源的分析,得其测点在垂直方向上的标准差为[9]
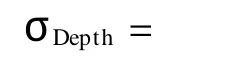

式中,σd1、σd2、σd3、σd4、σH、σdyn_draught、σWL、σZv分别为测距、波束指向角、纵摇角、波束角、升沉与诱导升沉、船体吃水、潮位推估和声线改正在垂直方向上的中误差,其中,横摇角与波束指向角误差可一并处理,表层声速的影响已归纳到σd2中。
而单波束测深系统仅包含吃水改正、声速改正和潮汐改正,故单波束测深测点在垂直方向上的标准差可表示为

则垂直不确定度σV可表示为[7]

2.1.4 不确定度信息的组织及应用
通过式(2)~(7),可算得各测深点相应的水平和垂直不确定度,某水深点i的信息可表示为Si= Xi,Yi,Zi,σHi,σVi,其中 Xi,Yi,Zi为测深点的平面坐标和水深值,σHi、σVi分别为水平和垂直不确定度。根据不确定度的定义[9],这一测点的实际水深真值应包含在区间内。
对水深数据进行前期整理和相关归算后,不确定度作为水深质量指标加入测点的相关信息中。
2.2 顾及不确定度的DDM内插方法
离散点构建格网DEM是在原始数据呈离散分布时使用的方法,其基本思路是选择一合理的数学模型,利用已知点上的信息求出函数的待定系数,然后求算规则格网点上的高程值[12]。随着水深数据向高密度、高精度方向发展,通常采用运算简单、执行效率高的距离幂次反比加权法来进行内插,一般选取离散点至节点的距离平方的反比为权重[13]。插值后节点的水深只受距离的影响,离散点离格网节点距离越远权重越小,距离越近权重越大,这种方法在使用等精度的离散数据时能起到较好的效果,而当数据精度存在较大差异时,未能突出高精度数据的有效利用。如图1所示,根据具有较大不确定度(精度相对较低)的离散点a1(虚线部分代表水平不确定度,双实线部分代表垂直不确定度)和较小不确定度(精度相对较高)的离散点 a2,在格网节点b上内插时,由于离散点 a1距离节点较近,尽管其不确定度较大,但在使用距离加权时会赋予其较大的权值,而不确定度较小但距离远的离散点 a2在参与格网节点的内插过程中起的作用却很小。

图1 顾及不确定度的离散点内插Fig.1 Interpolation considering uncertainy of data points
基于上述分析,在使用带有不确定度信息的离散水深数据进行格网内插时,主要可考虑到两个因素的影响,一是离散点到数据内插点的距离,二是离散点不确定度的大小。因此对于离散水深数据的权重配赋,本文综合考虑离散点与格网节点的空间相关性和离散点的不确定度指标,提出顾及距离远近和不确定度大小的水深数据格网内插模型(以下简称不确定度加权方法),表示为


2.3 水深内插点的不确定度估计
由于编辑后的每一个测深数据均带有其相应的不确定度,因此须考虑如何合理地将离散点的不确定度信息归算到内插节点上去,根据国际组织ISO制定的《测量不确定度表示指南》(即《Guide oftheExpression ofUncertainty in Measurement》,简称 GUM方法)可以合成节点的水深不确定度[14]。
2.3.1 GUM方法合成不确定度

式中,rxixj为 xi与 xj的自相关系数。
2.3.2 GUM方法合成节点水深不确定度
给定距离反比加权方法的内插模型为

式中,di表示内插节点与离散点的平面距离;Z表示内插节点水深值;Zi表示离散点水深值;距离权函数又因为 di=为给定节点,故经简单推算可知

基于GUM方法,将式(11)的 Z看做由多个观测量(d1,d2,…,dn,Z1,Z2,…,Zn)构成的观测结果y,代入式(10),经整理,得距离反比加权方法对于节点水深的不确定度为

而根据不确定度加权方法的内插模型,结合式(8)、式(9)、式(10),通过 GUM方法可计算出该模型的节点水深不确定度为

通过上述步骤,即可计算出两种方法关于节点的水深不确定度。
3 试验与分析
3.1 试验区域
本文选用试验数据,区域范围及数据来源如图2和表1所示。利用某次测量刚好扫过这些交界区域的多波束测线数据,选取结构合理、分布均匀的121个测深点作为检查点,如图2(b)所示。

图2 试验数据区域范围Fig.2 Area of experimental data

表1 各区域的测量时间及方式Tab.1 Surveying time and means of various areas
需要说明的是,由于区域3的测量时间比较早,当时的水深测量数据未有效考虑不确定度计算,很多信息未保留,无法准确计算其不同水深点的水平和垂直不确定度,只能根据数据来源,查询出当时的测图比例尺和测量方式,简单推算所有水深的精度指标,最后确定所有水深的水平和垂直不确定度依次统一为25 m和0.4 m。对于区域4的水深,来源于原海图数字化,根据海图成图规范的精度要求和海区的地形情况,粗略估计水平和垂直不确定度依次统一为50 m和0.5 m。
3.2 内插水深点的质量分析
为了验证模型的有效性,分析DDM内插质量。如图2(a)所示,分别从区域1、区域2、区域3、区域4、交界区域 a(区域1、2的交界区域)、b (区域2、3的交界区域)和c(区域3、4的交界区域)中各随机抽取5个检查点(图2(b)),其原始水深值作为比对值,将采用两种不同内插方法在检查点的内插值 Z与比对值Z′逐一比较,计算不同方法的内插值与比对值的水深差值ΔZ和垂直不确定度σv(由于内插点的平面坐标直接给定,故不需要考虑内插点的水平不确定度)。表2~表8列出了比较两种方法生成的内插结果。

表2 区域1的比对(只利用区域1的数据进行计算分析)Tab.2 Contrast of area 1(only data in area 1 is computed and analyzed) m

表3 区域2的比对(只利用区域2的数据进行计算分析)Tab.3 Contrast of area 2(only data in area 2 is computed and analyzed) m
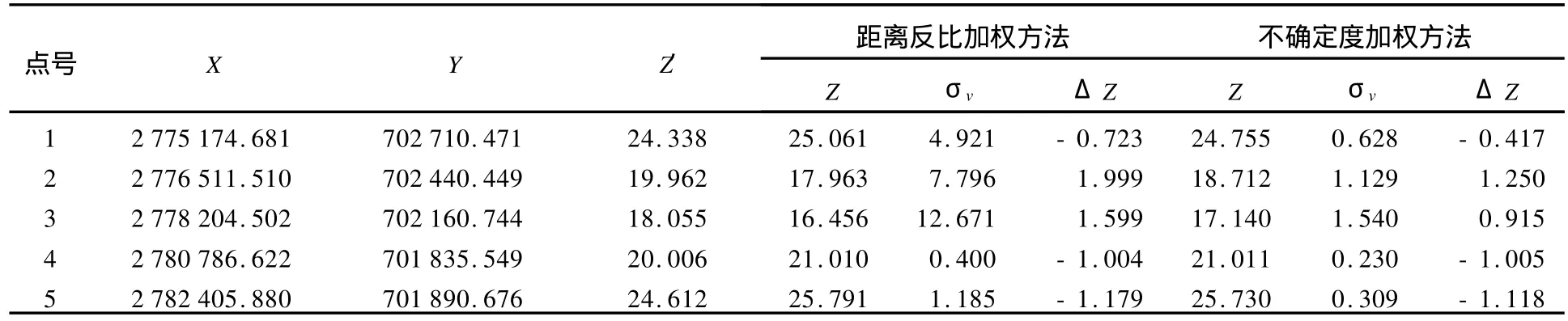
表4 区域3的比对(只利用区域3的数据进行计算分析)Tab.4 Contrast of area 3(only data in area 3 is computed and analyzed) m
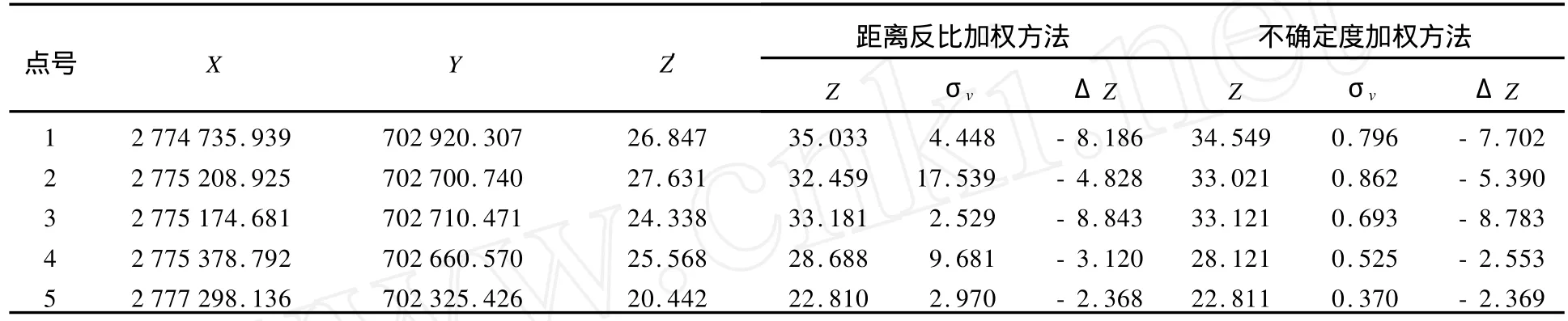
表5 区域4的比对(只利用区域4的数据进行计算分析)Tab.5 Contrast of area 4(only data in area 4 is computed and analyzed) m
表2~表5显示,当数据来源基本相同、不确定度相差很小时,不确定度加权方法相对于距离反比加权,在内插值与比对值的差值上没有明显提高。对于水深不确定度较小的区域(区域1、区域2),距离反比加权法和不确定度加权法内插的水深值与比对值相差都比较小,但采用不确定度加权法,能明显改善内插值的垂直不确定度。由于检查比对点的实测水深大部分垂直不确定度位于0.2~0.4之间,所以采用不确定度加权法的内插水深,几乎不会降低原始水深的内插质量。但对于水深不确度较大的区域(区域3、区域4),尽管采用不确定度加权法,在水深比对差值以及内插水深垂直不确定度指标上都有一定改善,但仍无法达到理想效果,应避免或慎重使用内插水深。
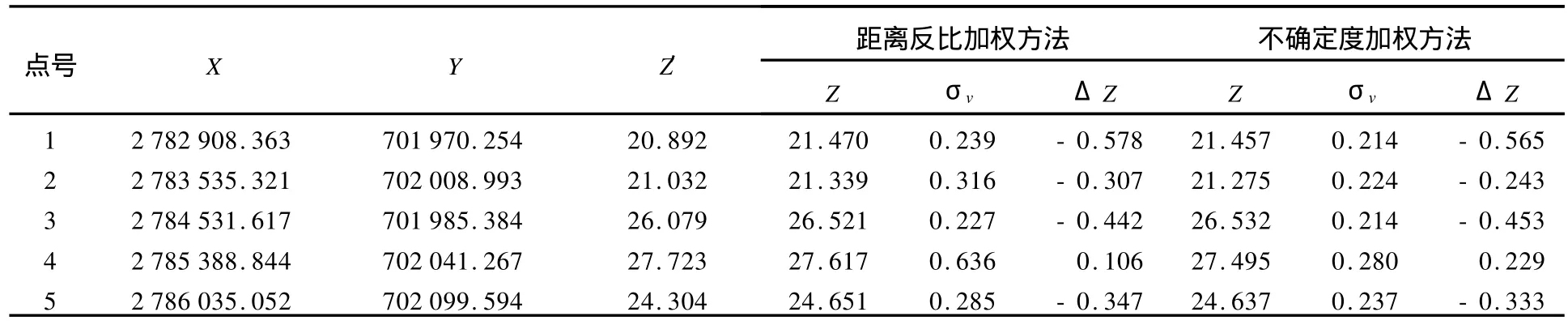
表6 交界区域a的比对(同时利用区域1、2的数据进行计算分析)Tab.6 Contrast of boundary areaa(data in area 1 together with area 2 are computed and analyzed) m

表7 交界区域b的比对(同时利用区域2、3的数据进行计算分析)Tab.7 Contrast of boundary areab(data in area 2 together with area 3 are computed and analyzed) m
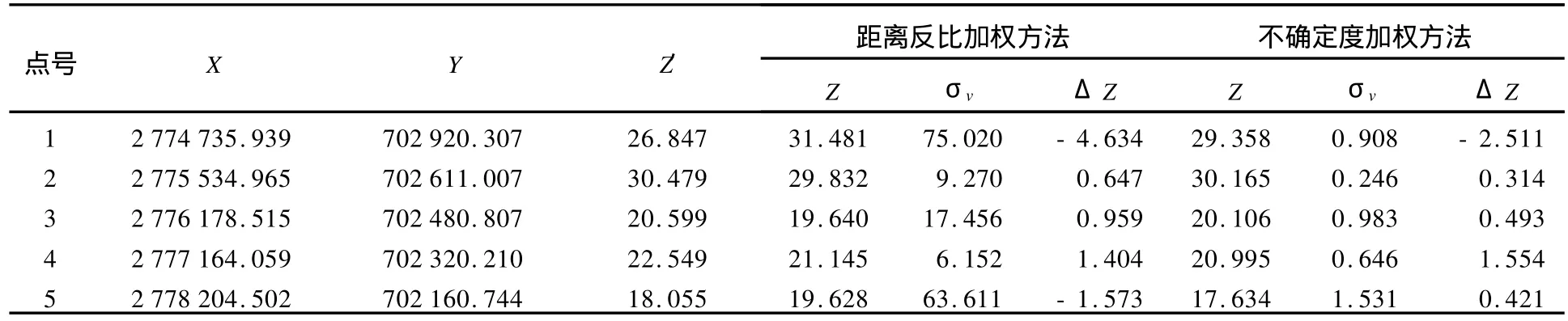
表8 交界区域c的比对(同时利用区域3、4的数据进行计算分析)Tab.8 Contrast of boundary areac(data in area 3 together with area 4 are computed and analyzed) m
从表6~表8中两种方法计算出的垂直不确定度可以看出,距离反比加权法内插水深的垂直不确定度相对较低,而不确定度加权法可有效改善内插节点的垂直不确定度。这种改善的程度与不同的数据源有关。当数据不确定度相差越大时,采用不确定度加权方法改善程度越高。
从表6~表8各比对点看,相对于距离反比加权法,不确定度加权法在大部分内插结果中其水深比对差值也有明显提高。虽然在极个别检查点处,不确定度加权法的内插值比距离反比加权内插值偏离原始检查数据略微偏大,但这是由于检查点数据也存在着一定的水深垂直不确定度引起的,这种偏大的程度要远小于水深垂直不确定度。
从表2~表8可以看出,每个内插水深后,都具有一个明确的垂直不确定值,从而为每个内插水深提供了详细的质量评估。
3.3 DDM总体质量分析
通过前面设定的121个检查点,对使用距离反比加权方法和顾及不确定度加权方法构建的海底DDM进行总体质量分析,设检查点的原始观测水深值为 Z′i(i=1,2,…,n),在建立DDM以后,由DDM内插出这些点的水深值为 Zi,则DDM质量采用以下公式评估

计算结果如表9所示,对比两种方法在区域1、2、3、4中的内插质量可以看出,当数据来源基本相同、不确定度相差较小时,不确定度加权法相对于距离反比加权法在内插质量上的提高不大;对比两种方法在交界区域a、b、c中的内插质量可以看出,两组数据的测量时间、测量方式、测量精度等相差越大,不确定度加权法相对于距离反比加权法在内插质量上的提高就越大。

表9 两种内插方法的质量对比Tab.9 Quality contrast of two interpolating methods m2
表9也显示,在水深不确定度较小的区域,采用距离反比加权法和不确定度加权法,其总体质量都能达到较高的标准,但从表2、表3发现不确定度加权法具有更优的水深垂直不确定度。但在水深不确度较大的区域(如区域4、交界区域c),两种水深内插方法都将会给内插点带来较大的中误差,这也是长期以来海洋测绘界谨慎或者避免使用水深内插方法的原因。但通过试验可以看出,无论是多波束测深或单波束测深,只要水深精度、密度达到一定程度,采用水深内插方法完全能够达到较高的准确度,为目前逐渐开始广泛使用的水深内插方法进一步奠定相应的理论依据。
4 结 论
通过分析、计算及试验比对,得结论如下:
(1)根据水深不确定度信息来进行权值配赋,明显提高了内插水深点的垂直不确定度,也同时提高了DDM的总体精度。当水深不确定度相差越大时,提高的程度越高。
(2)在水深不确定度较小的区域,距离反比加权法和不确定度加权法构建的DDM的总体质量都能达到较高的标准,但不确定度加权法可得到更优的水深垂直不确定度。而在水深不确度较大的区域,两种方法都无法满足水深内插的要求。但只要存在一定量的高质量数据,采用不确度加权内插方法,就能使内插水深达到理想效果。
(3)通过对水深不确度的传递与合成,突破了传统方法不能对内插水深进行质量评估的局限,实现了对每个内插水深的详细质量评估。
当然,由于本文研究所掌握的数据源有限,只是选取某一海图上来源不同的数据进行了试验,更多的数据源还有待于进一步的试验分析。同时,本文没有考虑数据综合处理及可能的海底地形变化对水深内插结果比对的影响,还没有仔细思考研究所得结论如何规范化地去指导实际作业,这都有待于以后进行更深入的分析和探索。
[1] SMITH S.The Navigation Surface:a Multipurpose BathymetricDatabase [D]. Durham:University of New Hampshire,2003.
[2] Naval Institute of Hydrographic Surveying and Charting. GB12327-1998 Specifications for Hydrographic Survey[S]. Beijing:Chinese Standard Press,1999.(海军海洋测绘研究所.GB12327-1998海道测量规范[S].北京:中国标准出版社,1999.)
[3] Naval Press.GB12320-1998 Specifications for Chinese Nautical Charts[S].Beijing:Chinese Standard Press, 1999.(海军出版社.GB12320-1998中国航海图编绘规范[S].北京:中国标准出版社,1999.)
[4] ZHANG Lihua.A Study on Drawing Depth Contours Using Grids Based on Irregular Area,Arbitrary Direction and Different Scale in Bathymetric Survey for Port Engineering[J].Port&Waterway Engineering,2005, 375(4):9-13.(张立华.港口工程水深测量中的不规则区域、任意方向、不等尺度网格法追踪等深线研究[J].水运工程,2005,375(4):9-13.)
[5] GAO Jinyao,JIN Xianglong,WU Ziyin.Construction of Submarine DTM from Raw Multibeam Data[J].Marine Science Bulletin,2003,22(1):30-38.(高金耀,金翔龙,吴自银.多波束数据的海底数字地形模型构建 [J].海洋通报,2003,22(1):30-38.)
[6] J IA Juntao,ZHAI Jingsheng,MENG Chanyuan,et al. Construction and Visualization of Submarine DEM Based on Large Number of Multibeam Data[J].Journal of Geomantics Science and Technology,2008,25(4):255-259.(贾俊涛,翟京生,孟婵媛,等.基于海量多波束数据的海底地形模型的构建与可视化[J].测绘科学技术学报,2008,25(4): 255-259.)
[7] WANG Zhongyu,LIU Zhimin,XIA Xintao,et al.Measurement Error and Uncertainty Evaluation[M].Beijing: Science Press,2008.(王中宇,刘智敏,夏新涛,等.测量误差与不确定度评定[M].北京:科学出版社,2008.)
[8] IHO.S-44 IHO Standards for Hydrographic Surveys[S]. 5th.ed.Monaco:International Hydrographic Bureau,2008.
[9] WU Chao,YIN Xiaodong,ZHANG Lihua,et al.The Method of Quality Estimation in Multibeam Sounding Data Based on Uncertainty[J].Hydrographic Surveying and Charting,2009,29(3):11-15.(吴超,殷晓冬,张立华,等.基于不确定度的多波束测深数据质量评估方法 [J].海洋测绘,2009,29(3):11-15.)
[10] TAO Benzao.Basic Theory of Uncertainty of Quality Control in GIS[J].Journal of Institute of Surveying and Mapping 2000,17(4):236-238.(陶本藻.GIS质量控制中不确定度理论 [J].测绘学院学报,2000,17(4): 236-238.)
[11] HUANG Motao,ZHAI Guojun,XIE Xijun,et al.The Influence of Carrier’s Attitude and the Position Reduction in Multibeam Echosounding and Airborne LaserDepth Sounding[J].Acta Geodaetica et Cartgraphica Sinica, 2000,29(1):82-88.(黄谟涛,翟国君,谢锡君,等.多波束和机载激光测深位置归算及载体姿态影响研究[J].测绘学报,2000,29(1):82-88.)
[12] L I Zhilin,ZHU Qing.Digital Elevation Model[M]. Wuhan:Wuhan University Press,2003.(李志林,朱庆.数字高程模型[M].武汉:武汉大学出版社,2003.)
[13] L I Jiabiao.Multibeam Sounding Survey:Principles, Technologiesand Data Processing Methods [M]. Beijing:Ocean Press,1999.(李家彪.多波束勘测原理技术与方法[M].北京:海洋出版社,1999.)
[14] International Organization for Standardization.Guide of the Expression of Uncertainty in Measurement[M]. XIAO Mingyao,KANG Jinyu,trans.Beijing:Chinese Metrology Press,1994.(国际标准化组织.测量不确定度表示指南[M].肖明耀,康金玉,译.北京:中国计量出版社,1994.)
A Method for Interpolating Digital Depth Model Considering Uncertainty
ZHANGLihua,J IA Shuaidong,WU Chao,YIN Xiaodong
Department of Hydrograhy and Cartography,Dalian Naval Academy,Dalian 116018,China
A method for interpolating digital depth model(DDM)considering uncertainty is proposed.The uncertainty of the soundings deriving from the different data sources is calculated,the interpolation model by using the uncertainty in weighting for the soundings is constructed,and the uncertainty of the interpolated depth node is estimated.Experimental results demonstrate that the proposed method has improved the quality of DDM and can estimate the uncertainty of the interpolated depth node.
digital depth model;uncertainty;interpolotion
ZHANG Lihua (1973—),male,PhD, associate professor,majors in marine GIS.
1001-1595(2011)03-0359-07
P229
A
国家863计划(2009AA12Z202);国家自然科学基金(40801189)
(责任编辑:雷秀丽)
2010-04-13
2010-09-01
张立华(1973—),男,博士,副教授,主要从事海洋GIS研究。
E-mail:zlhua@163.com

