一类具有分布时滞的p-Laplacian中立型泛函微分方程周期解的存在性

黄祖达，熊万民，贾仁伟

(湖南文理学院数学与计算科学学院，湖南常德 415000)

一类具有分布时滞的p-Laplacian中立型泛函微分方程周期解的存在性

黄祖达，熊万民，贾仁伟

(湖南文理学院数学与计算科学学院，湖南常德 415000)

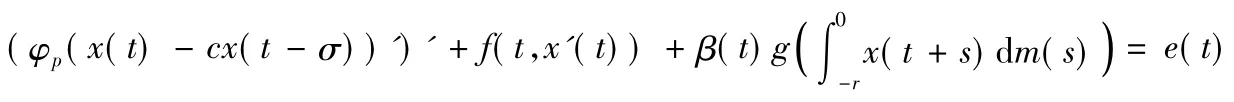
分布时滞;p-Laplacian中立型泛函微分方程;周期解;Mawhin重合度

首先，p-Laplacian算子是指φp:R→R，φp(u)=|u|p－2u(p＞1).近些年来，对p-Laplacian中立型泛函微分方程周期解的存在性问题引起了广泛探讨，取得了一些结果［1－4］.然而，对具有分布时滞的p-Laplacian中立型泛函微分方程周期解问题的研究并不太多，文献［5］研究了一类具有分布时滞p-Laplacian中立型泛函微分方程

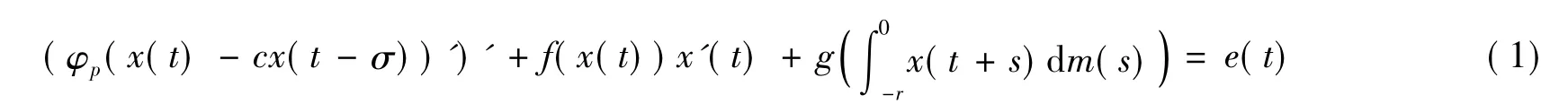
的周期解的存在性问题，在p＞2的条件下，利用重合度理论获得了方程(1)至少存在一个周期解的充分条件.受以上文献及引用文献的启发，本文研究了下面一类具有偏差变元的p-Laplacian中立型泛函微分方程

1 准备知识

为行文方便，先引入以下记号:

定义投影算子P，Q如下

2 主要结果

定理1如果下列条件满足:

则方程(2)至少存在一个T－周期解.

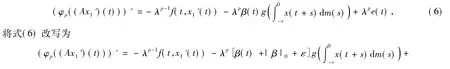
下面分2种情形讨论

则方程(1)至少存在一个T－周期解.

4 举例

给出下列方程

故由定理1可知，以上方程至少有一个2π周期解.

［1］PENG Shi-guo，ZHU Si-ning.Periodic solutions for p-LapIacian Rayleigh equalions with a deviating argument［J］.Nonlinear A-nalysis，2007，67:138 －146.

［2］LU Shi-ping.Existence of periodic solutions to p-Laplacian equation with a deviating argument［J］.Nonlinear Analysis，2008，68:1453－1461.

［3］ CHEUNG Wing-sum，REN Jing-li.Periodic solutions for p-Laplacian Rayleigh equations［J］.Nonlinear Analysis，2006，65:2003－2012.

［4］彭世国.具有偏差变元的p-Laplacian中立型Lienard方程的周期解［J］.数学年刊，2008，29A(5):617－626.

［5］朱艳玲，汪凯.具有p-Laplace算子的中立型泛函微分方程周期解［J］.系统科学与数学，2009，29(6):808－817.

［6］LU Shi-ping，GE Wei-gao，ZHENG Zu-xiu.Periodic solutiolls to lieuiral differential equalion with deviating arguments［J］.Appl.Math.Comput，2004，152:17 －27.

［7］HALE J K.Theory of Functional Differential Equations［M］.New York:Springer-Verlag，1997.

［8］GAINES R E，MAWHIN J L.Coincidence degree and nonlinear differential equation［M］New York:Springer-Verlag.1997.

Periodic Solutions for a Class of p-Laplacian Neutral Functional Differential Equation with Distributed

HUANG Zu-da，XIONG Wan-min，JIA Ren-wei
(College of Maths.＆ Computing Science，Hunan University for Arts and Science，Changde 415000，China)

distributed;p-Laplacian neutral functional differential equation;periodic solutions;Mawhin coincidence degree

O 175.14 < class="emphasis_bold">文献标志码:A

A

1004－1729(2011)01－0011－09

2010－11－05

国家自然科学基金项目(10801047);湖南文理学院芙蓉学院重点课题项目

黄祖达(1964－)，男，湖南常德人，湖南文理学院数学与计算科学学院讲师.