曲线拟合度分析法在公路货运回归预测中的应用
吴汪友 ,孙秋高
(浙江交通职业技术学院运输管理学院,浙江杭州 311112)
曲线拟合度分析法在公路货运回归预测中的应用
吴汪友 ,孙秋高
(浙江交通职业技术学院运输管理学院,浙江杭州 311112)
对曲线拟合度分析法的基本原理进行了介绍,阐述了回归预测中引入曲线拟合度分析法的作用,并选取杭州市“十一五”期间货运量与生产总值数据构建若干回归预测模型,通过曲线拟合度比较分析,优化了预测模型选择.实验结果表明该方法所获得的模型预测结果相对接近于实际.
曲线拟合度;运输量;周转量;回归预测
公路货运量预测是交通规划的重要内容,是行业主管部门管理的依据,也是项目立项、决策、确定建设规模等最基础的依据之一.公路货运量(货运量、货物周转量)是在一定时期内公路实际运送的货物吨数,是反映运输业为国民经济和运输业生产效果的数量指标,也是研究市场经济发展速度的重要指标.公路货物周转量是指在一定时期内,由公路实际完成运送过程的以重量和运送距离的复合单位(吨公里)计算的货物运输量,不仅包括运输对象的数量,还包括了运输距离的因素,因而能够全面地反映运输生产成果.
目前,国内外货运量预测中,通常采用有组合模型[1]、无偏灰色预测模型[2-3]、RBF 神经网络[4]、回归曲线模型等多种形式[5],其中回归曲线模型是一种具体的、行之有效的、实用价值很高的预测途径,因而在预测中常常被选用.由于运输系统是社会经济系统的一个子系统,社会经济的发展水平决定了运输需求的发展水平;另一方面,运输业的快速发展又会反过来促使社会经济系统的快速发展,二者之间具有十分密切的关系.通过分析历年生产总值和货物运输量、货物周转量的数据,可以得出其具有较强的正相关性,基本符合回归预测的条件.由于回归预测模型类型较多,致使预测方法很难选择,不同的模型预测结果与实际的差距,无论在精度上还是在可靠性方面都不尽相同[6].通过引入曲线拟合度分析方法,有利于在具体预测决策过程中选择比较适当的回归预测方法,从而提高预测的准确性和可靠性.
1 曲线拟合度分析法应用的基本思路
回归预测法是预测学的基本方法,在分析自变量和因变量之间相关关系的基础上建立变量之间的回归方程,并将回归方程作为预测模型,根据自变量在预测期的数量变化来预测因变量.根据历年统计资料显示,地区生产总值与货物运输量、货物周转量的数据之间呈现较强的正相关性,符合回归预测基本条件,因此,预测的总体思路就是构建回归曲线来推算道路运输量的发展趋势.
在货运量预测过程中,利用地区生产总值和货物运输量、货物周转量因素(自变量)之间的相互关系,建立变量间的数量关系近似表达的函数方程,并进行参数估计和显著性检验,再运用回归方程式预测因变量数值变化.依此原理,地区生产总值和货物运输量或生产总值和货物周转量可以形成一元二次、一元三次、混合、对数、指数、逆矩阵、幂函数等7种曲线回归预测模型进行货运量的预测分析[7],如表1所示.

表1 回归预测模型
由于上述运输量回归预测原理不尽不同,预测的结果也有较大的区别.为了提高预测的有效性,采用专业数据SPSS分析软件,根据函数曲线的拟合度及曲线发展趋势等评价指标,为最终选择何种预测模型提供参考依据.统计学是通过构造统计量R2(曲线的拟合度或称相关指数)来量度的,R2可由样本数据计算得出.线性曲线和非线性曲线的拟合度判定也可以利用判断R2的方法,这个判断标准在实践中也被证明是符合实际的[8-9],R2较大的曲线模型,往往也是拟合较好的模型.若建立的模型愈接近于实际,则R2愈接近于1.曲线拟合度分析是对已制作好的预测模型进行分析,比较其预测结果与实际发生情况的吻合程度,通过对数个预测模型同时进行分析,比较R2大小,选其拟合度较好的预测模型进行试用.
2 回归曲线拟合度分析法应用实例
2.1数据来源通过选取近10年来杭州的货运量与生产总值数据来构建公路货物运输量预测模型,以此对“十二五”期间货运量进行预测.
根据2000—2010年的杭州市统计年鉴[10],地区生产总值与货物运输量、货物周转量数据之间呈现较强的正相关性,可以构建成一元二次、一元三次、混合、对数、指数、逆矩阵、幂函数等7种曲线回归预测模型.回归预测与分析所需相关数据如表2所示.

表2 杭州“十一五”期间国民经济和公路货物运输量
2.2 模型建立与最优模型选取首先,根据表1中7种运输量预测模型,分别建立回归预测方程;其次,根据函数曲线的拟合度及曲线发展趋势等评价指标,对比7种不同曲线的数据拟合度及曲线发展趋势等评价指标;最终确认最优的预测模型.货物运输量、货物周转量在不同模型曲线下的拟合度对比分析如图1所示.
根据曲线拟合度越接近1,则预测模型越接近实际,预测的数据可信度就越高.通过货物运输量在不同模型曲线下的拟合度对比分析,其中R2=0.970最高,对应货物运输量的最优预测模型为逆矩阵函数预测模型.因此,具体方程为
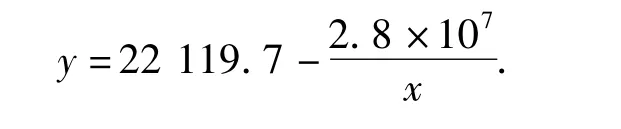
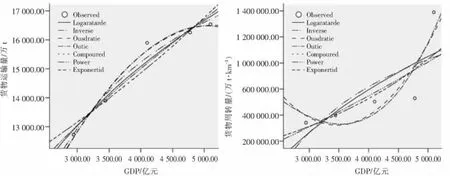
图1 曲线拟合度对比
同理,对货物周转量7种预测模型曲线中曲线拟合度对比分析,R2=0.807为最高,其对应最优货物周转量预测模型为一元三次函数预测模型,具体方程为
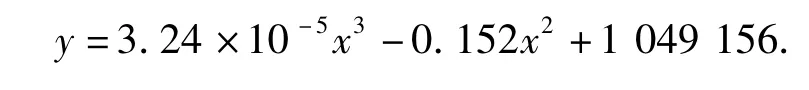
3 优化后回归预测模型预测与应用分析
3.1 货运量回归模型预测根据上述模型,杭州“十二五”期间公路运输量预测值如表3所示,货物运输量、货物周转量的预测及发展趋势如图2所示.据预测,“十二五”期间杭州货物运输量年平均增长率为2.36%,2015年货物运输量为19 019.81万t;货物周转量年平均增长率为4.43%,2015年货物周转量为12 524 932 万 t·km-1.
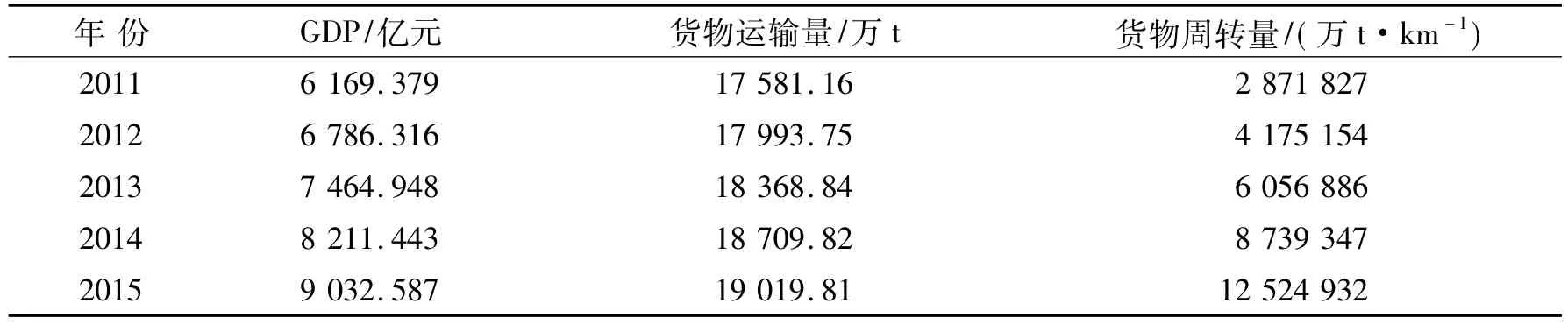
表3 杭州“十二五”期间公路货物运输量
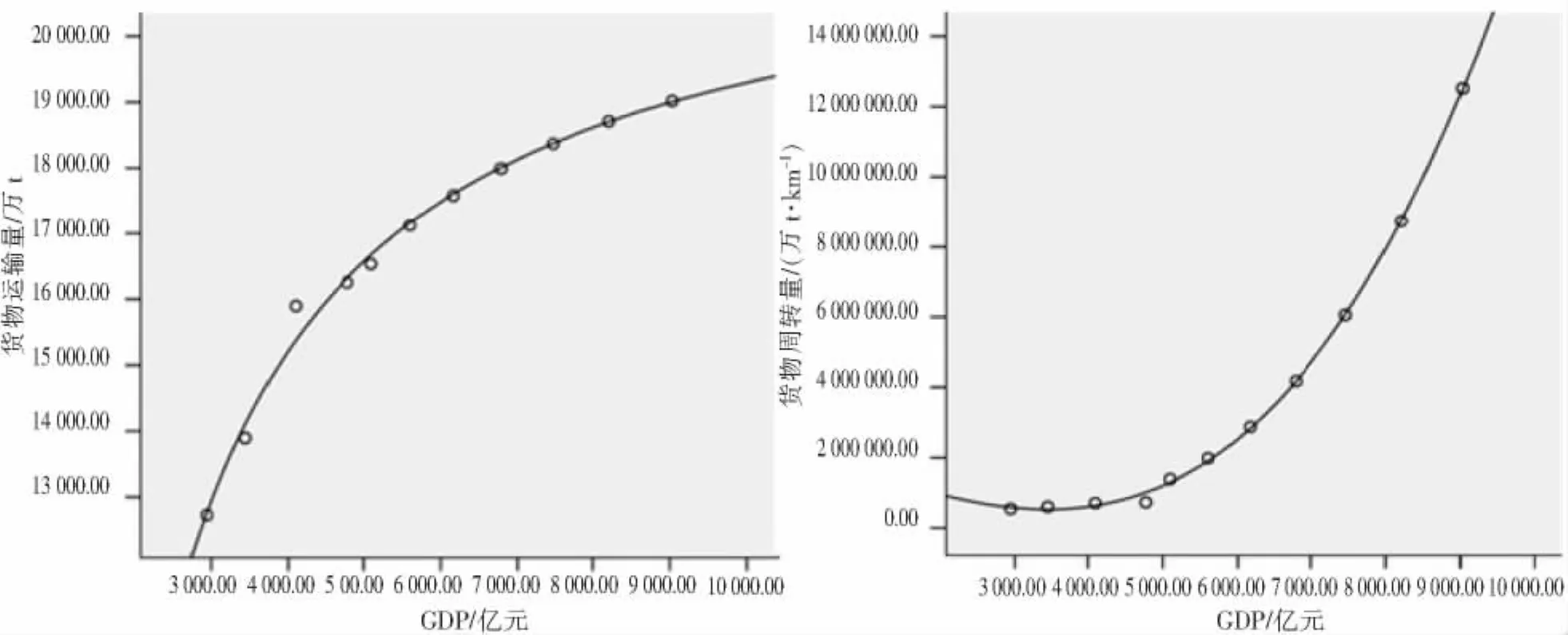
图2 货物运输量、货物周转量预测趋势
3.2 货运量预测结果分析通过上述公路货运预测数据的分析,杭州“十二五”期间道路运输业货物运输量增速放缓、货物周转量止跌回升.为了进一步说明回归曲线拟合度分析法的应用效果,对预测结果与实际发展趋势是否一致,笔者从以下2个方面进行了详细解析.
1)其他运输设施快速发展,对公路运输形成巨大的挑战.近十几年来,以高速公路为代表的高等级公路网络的建设,为公路货运提供了良好的运输条件,有力地促进了公路运输量的增长.但也不能忽视的是,近几年铁路逐步实现高速化,从而也直接影响了公路运输量的增长.通过杭州市近5年公路运输统计资料分析,公路货物运输量在国民经济公路贡献率呈现下降趋势,且年货物运输量增幅也呈现下降趋势,这与铁路网络不断完善和提速存在一定的关联性,也与公路、铁路各自所具有的优势相匹配,但不可否认的是,公路运输具有更多的承担物流末端货物的分散与聚集功能.
2)运输量增速放缓,周转量增长加快,二者表面上相矛盾.对近5年来杭州市运输量和周转量进行了分析与预测,结果表明,运输量增速放缓,周转量止跌回升,增长迅速.由于周转量等于货物重量和运送距离乘积,反映出运输距离呈急剧增长趋势.相对其他运输工具而言,中短途公路“门对门”运输更为经济和实际,对于运输企业来说要用长途运输很难解释,这主要是道路运输企业由传统运输业向地区配送业转型,在一定程度上表明我国公路运输行业逐步迈向更高层次.通过对近些年来我国公路货物运输企业的实地调查,发现道路运输企业更多的是从事中短距离货物分拨、配送和揽货业务,从而充分发挥物流末端货物分散与聚集功能,开展“门对门”运输业务.但由于客户分散,网点众多,也增加了货物运输距离,因此,现实情况与运输量和周转量的发展趋势不相矛盾.
3.3 预测模型优化的运用由于上述公路货运量预测克服了以主观随意确定预测模型的弊端,通过引入回归曲线的拟合度及曲线发展趋势等评价指标,根据R2的大小来判断是否较为合适的模型,以此来提高预测结果相对贴近实际.本文的货运量预测方法成功用于杭州市道路运输业“十二五”发展规划,所获预测数据较为客观、真实地反映未来杭州道路运输业发展趋势,对其他预测也具有较强的借鉴意义.但应注意的是,在具体预测中,需要引用时间跨度相对较长的数据,以便提高预测结果的准确性.此外,由于其他运输体系持续建设和道路运输行业不断转型,在一定程度上影响回归曲线拟合度分析法在货运量预测应用的效果,因而对预测所获得数值还需要从深层次进行分析.
4 结论
由于可供选择回归预测模型相对较多,而且基本上都能反映出生产总值与运输量之间正相关的关系,但每一个模型都会得到一个不同的发展趋势,预测数值与实际情况的差距也不尽相同.根据地区生产总值与货运量、货物周转量之间的正相关关系,分别建立若干回归曲线模型,应用曲线拟合度分析法,克服了随意选择一种回归模型很难精确推算货运量的弊端.在公路货运量预测中,引入曲线拟合度分析法进行预测,所获预测货运量较为准确,方法基本可行,预测结果基本符合杭州市未来道路货运发展趋势,对其他预测也具有较强的借鉴意义.
[1]郝佳,李澜,铁路货运量组合预测模型的研究[J].铁道运输与经济,2004,26(11):73-75.
[2]蔡家明.货运量多维灰色模型的预测[J].上海工程技术大学学报,2005,19(1):38-41.
[3]边浩毅,王怡民.基于灰色预测模型的公路运输量预测[J].江南大学学报:自然科学版,2006,5(6):745-748.
[4]王登.基于人工神经网络的货运量预测模型研究[J],物流工程与管理,2009,31(3):28-29,31.
[5]赵卫艳,谷雪松.线性回归模型在货运量预测中的应用[J].山西建筑,2007,33(9):248-249.
[6]蒋惠园,杨大鸣.货运量预测方法的比较[J].运筹与管理,2002,11(3):74-79.
[7]赵卫亚,彭寿康.计量经济学[M].北京:机械工业出版社,2008:34-60.
[8]董玉恒,白求恩.曲线拟合度和拟合优度检验的局限性及新设想[J].现代预防医学,1996,23(3):137-138.
[9]王红芳.集对分析在频率曲线拟合度定量评价中的应用[J].水利水电技术,2007,38(4):1-3,15.
[10]浙江省统计局国家统计局浙江调查总队.浙江省统计年鉴[M].北京:中国统计出版社,2009:546-547.
Application of Curve Fitting Analysis Method in the Road Freight Regression Forecast
WU Wang-you,SUN Qiu-gao
(Department of Management for Transportation,Zhejiang Vocational and Technical College for Traffic,Hangzhou 311112,China)
In the paper,the basic principle of the curve fitting degree analysis method was introduced,and the function of the method for regression forecast was discussed.The data of freight and GDP in Hangzhou during“Eleventh Five-Year”period was used to construct several regression models,and the method was used to optimize the model.The results indicated that the prediction data of the obtained model were relatively close to that of the actual trend.
curve fitting;traffic;turnover;regression forecast
U 49 < class="emphasis_bold">文献标志码:A
A
1004-1729(2011)01-0049-04
2010-08-09
吴汪友(1976-),男,安徽安庆人,浙江交通职业技术学院运输管理学院讲师,硕士.

