服从离散有限马尔可夫链的期权定价模型探讨

刘 薇

(湖南财政经济学院,湖南长沙 410205)

服从离散有限马尔可夫链的期权定价模型探讨

刘 薇

(湖南财政经济学院,湖南长沙 410205)

Black-Scholes期权定价模型是假设在期权有效期内,标的资产收益波动率和无风险利率是恒定不变的。但现实中波动率和利率受许多不确定性因素的影响而总是一个变量。在波动率服从时间离散,状态离散有限且时齐的马尔科夫过程的期权定价模型的基础上,探讨当利率和波动率都是随机变化时的期权定价模型,并给出欧式看涨期权的定价方法。

波动率;利率;离散有限马尔可夫链;期权定价

1973年,美国芝加哥大学学者 Black F.与ScholesM.提出了 Black-Scholes期权定价模型(以下简称 “BS模型”),对股票期权的定价作了详细的讨论[1]。期权是具有重要经济影响的金融衍生工具之一,从BS模型中不难发现,利率和波动率是影响期权定价的两个因素。标的资产价格波动率是期权定价模型输入变量中唯一的无法由市场直接提供的参数,它受宏观经济因素、特定事件、投资者心理状态等因素的影响而总是一个变量。利率是影响期权价值的另一个重要因素。在短期情况下,一般都认为市场利率是稳定的,可以看作常数;但若是进行长期投资,由于国家政策、经济发展状况以及股市的起伏等多种因素都会引起市场利率的波动,因此利率也不能以一个常数来恒定。

近年来,国内外学者在期权定价的理论研究上取得了不少成果:如Merton提出了随机利率模型的期权定价理论[2];Stein E.研究出了转移扩散模型的股票期权定价理论[3];刘文平、李萍等在利率服从马尔可夫过程的条件下对期权定价模型进行了研究[4]等等。笔者借鉴已有成果,在波动率服从时间离散,状态离散有限且时齐的马尔科夫过程的期权定价模型[5]的基础上,探讨当利率和波动率都是随机变化时,即波动率和利率都服从时间离散,状态离散有限且时齐的马尔科夫链的期权定价模型,并在此模型下给出了欧式看涨期权的定价公式。

一、BS期权定价模型简介

一般的,BS期权价格与 6个参数有关,即 St—标的资产价格(股价);K—期权的敲定价格(执行价格);T-t距期权的到期时间;r—无风险利率;σ—标的资产价格波动率;μ—股票的期望收益率。每个因素的变化对期权价格都有不同的影响。

1965年,保罗·萨缪尔森提出股价模型[6]:

利用上式以及 It^o公式,可得 t时刻股票价格为:

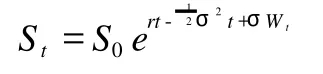
上式表明在等价鞅测度 P＊下,风险资产 St在 t=T时刻的预期收益率与无风险证券的收益率相同。在BS模型中,在每个时刻的期权价格都可通过在同样的概率测度 P＊下对终端值的条件期望来给定:

其中 h=(ST-K)+=F(ST),即 t时刻的期权价格可以表示为时间和标的资产价格的函数。

二、离散有限的期权定价模型

假定波动率和利率服从某个随机过程,且股票价格遵循几何布朗运动:

dSt=r(t)Stdt+σ(t)StdBt, 其中, {σ(t),t≥0},{r(t),t≥0}均服从时间离散,状态有限的马尔可夫链,且波动率和利率是相互独立的。

把一个样本期等分为 l个连续的时间间隔Δt,波动率的 k个状态空间为:

12k1{1,2…k},利率 r(t)∈G,G= {r1, r2,…,r

N},其中N为自然数。利率水平的每个取值 ri为一个状态。

1、构造一步转移概率矩阵

当波动率不变时 ^Pij(Δt),记为在两个连续的时间间隔中,利率水平从前一个时间间隔Δt的状 ri态转移到后一个时间间隔Δt的状态 rj的概率。于是构造出一步转移概率矩阵:

其N步转移概率矩阵即为一步转移概率矩阵的N次方 ^PN。由马尔可夫性知,^Pij(Δt)仅依赖于前一个Δt时间的利率状态,而与其以前的状态无关,因此可得一个马尔可夫链。

假设在任意时刻 t,波动率状态为σi,利率为rm,经过一步转移以后波动率状态为σj,利率为 rn。则一步转移概率可以表示为:

又因为波动率和利率是相互独立的,所以

从而可以构造出一步转移概率矩阵 P(Δt)。

假设到期日 T=nΔt,则由 Chapman-Kolmogorov方程可求得 n步转移概率(nΔt),其恰好是 n个一步转移概率矩阵的乘积,其中

2、股票价格波动率和利率的预测模型

由全概率公式可得 T时刻股票价格波动率的绝对概率分布为:

三、服从离散有限马尔可夫链的欧式看涨期权定价

以欧式看涨期权为例,其价格是欧式看涨期权到期日的期望值的贴现。考虑利率和波动率是服从时间离散,状态离散有限且时齐的马尔可夫链。

假设 t时刻,市场要求的风险溢价为 0,那么在t时刻当利率水平处于 ri状态时要求的一期回报率为ρi(Δt)=riΔt,则一期回报率的折现因子表示为:exp{-ρi(Δt)}=exp{-riΔt}。

对任意一种债券,假设 X(t)=(x1(t),x2(t),…,xN(t))T(T表示转置)为其在 t时刻的现金流,那么在 t-Δt时刻的折现现金流为:

用矩阵可以表示为:

令 Ω (Δt)= ≜ diag(e-ρi(Δt)),D(Δt) ≜ P^ ·Ω(Δt),其中 ,dij(Δt)=p^ij(t)e-ρi(Δt),i=1,2 …N,则 D(Δt)为一期的折现状态价格矩阵,有 X(t-Δt)=D(Δt)X(t)。

从而,可知 H(T)表示 T期状态价格的折现矩阵。

设现在时刻为 t,要经过 n步才能到达到期时刻T,则期权的定价公式为:

四、结论

传统的BS期权定价模型中,都是假定利率和波动率在期权的生命期内为常数。然而,投资者如果要进行长期投资时,由于国家宏观政策,经济发展状况以及股市的起伏等多种因素都会引起市场利率和金融资产收益的波动率的不稳定,使得利率和波动率都为一随机变量,且具有无后效性。因此,摒弃利率和波动率在期权有效期内恒定不变的假设条件,来探讨当利率和波动率都是随机变化时期权的定价模型,并给出此模型下欧式看涨期权的定价公式,具有一定的现实意义。但笔者仅讨论了利率和波动率都是随机变化的情况,在后续的研究中还可对波动率和利率的以下几种情形进行讨论:一是利率恒定,波动率服从时间连续,状态离散有限且时齐的马尔科夫过程的期权定价模型;二是利率恒定,波动率服从时间连续,状态离散可数且时齐的马尔科夫过程的期权定价模型。

[1]Black F,ScholesM.The valuation of options and corporate liabilities[J].Journalof Political Economy,1973,(81):637-654.

[2]Merton R C.Option Pricing when Underlying Stock Return Are Discontinuous[J].Journal of Financial Economics,1976,3:125-144.

[3]Stein E,Stein J.Stock price distributionswith stochastic volatility:an analytic approach[J].The Review of Financial Studies,1991,(4):727-752.

[4]刘文平,李 萍(等).利率服从马尔科夫过程时的期权定价 [J].华中师范大学学报(自然科学版),2004,38(2):153-155.

[5]靳绍礼,金朝嵩 .标的资产价格波动率服从有限马尔可夫链的期权定价 [J].重庆商学院学报,2002,(5):54-56.

[6]Samuelson P.A.Rational Theory ofWarrant Prices[J].IndustrialManagement Review,1965,(6):13-31.

Option Pric ing with Follow ing D iscrete L im itedMarkov Cha in

LIU Wei
(Hunan University of Finance And Econom ics,Changsha Hunan 410205)

The Black-Scholes option pricingmodel is constructed based on the following hypothesis:in the period of validity,the interest rate without venture and vibration rate of financial asset is invariable.But the realistic situation is not in such case.Because vibration and interest rates affected by lots of uncertain factors is always one variable.On the basisof option pricingmodel in which the vibration rate obeys discrete t ime,discrete,limited and homogeneous state ofMarkov chain,analyzing the option pricingmodel that interest rate and vibration rate are at random changes,and the European call option pricingmethod are made.

interest rate;vibration rate;discrete and limitedMarkov chain;option pricing

F224.7

A

2095-1361(2011)03-0104-03

2011-04-21

湖南省自然科学基金项目“随机环境中马氏链及其在金融中的应用”(项目编号:07A003)阶段研究成果之一

刘 薇(1983- ),女,湖南岳阳人,湖南财政经济学院教师,研究方向:数理金融

(编辑:惠斌;校对:朱恒)