在大学物理课程中利用Excel电子表格作数值计算

蒋卫建 胡 昉 方本民

(浙江大学宁波理工学院公共基础部,浙江宁波 315100)

在大学物理课程中利用Excel电子表格作数值计算

蒋卫建 胡 昉 方本民

(浙江大学宁波理工学院公共基础部,浙江宁波 315100)

在大学物理课程中,通常均要求作解析计算,而不涉及数值计算.本文以简谐振动、行星运动、双星系统的运动、限制性三体等问题为例介绍了用 Excel电子表格作数值计算,求解运动方程的办法.数值计算的思路简单明了,更有助于理解物理知识.随着计算机普及,学生利用计算机的能力提高,在大学物理课程中介绍利用 Excel作数值计算是有益的.

Excel;数值计算;大学物理;运动方程

1 引言

大学物理课程中所涉及的计算,例如应用牛顿定律求解运动方程等,均要求作解析计算.这样存在一定的弊病,一方面,大学生刚开始接触微积分,解析计算能力较差,求解微分方程有困难,影响对物理知识的理解.另一方面,有一些物理内容简单但解析计算困难的问题,大学物理课程就不能涉及了.另外,物理学是实验科学,计算结果的检验最终是要与实验比较,完全精确解的意义不大.所以,在大学物理课程中,可以适当引入数值计算.

在20世纪60年代,电子计算器刚开始普及,个人计算机刚出现,费恩曼物理学讲义[1]中,就列出表格,用计算尺或计算器作数值计算,帮助理解运动方程的含义,并指出可以用同样的方法来计算太阳系中行星的运动.如今,计算机已十分普及.大学生几乎人人有计算机,能使用微软公司的Office软件.可以利用Office软件的组件之一,电子表格软件 Excel,遵循费恩曼的方法,在大学物理课程中引入数值计算.

2 牛顿定律求解运动方程的含义

如果知道t时刻物体的位置和速度,就可以算出t+Δt时刻物体的位置.当Δt很小时,可以采用以下近似公式

如果还知道 t时刻物体的质量和所受的力,根据牛顿第二定律,F=ma,就可以求得 t时刻的加速度,也就可以根据加速度来求得 t+Δt时刻的速度.在Δt很小时,可以采用以下近似公式

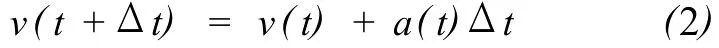
这样,有了t+Δt时刻的物体的位置和速度,由此重复,可以计算出 t+2Δt,t+3Δt,…时刻物体的位置和速度,也即所有时刻物体的位置和速度.这就是用牛顿定律求解运动方程的含义.

为了减少计算的次数,增加准确度,再仔细地分析一下以上的计算过程.以上近似公式(1)中,采用的是t时刻的速度来计算t+Δt时刻物体的位置.但是,因为加速度不为零,所以在 t～t+Δt这段时间内速度是在不停地变化的.应该采用其间哪个时刻的速度呢?可以采用 t+Δt/2时刻的速度.这样有

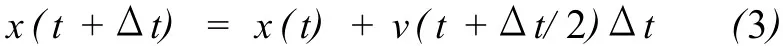
同样,计算速度时采用 t+Δt/2时刻的加速度,有

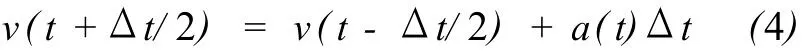
最后,对于初始时刻,已知 t=0时的位置和速度,可以用一个特殊的公式来计算 v(Δt/2),即

3 简谐振动

先来看简谐振动,假设 k/m=1,有

在 Excel表格中依次输入表1的内容,包括公式[2].

Wij表示元素组Ci和Cj之间元素的相对重要度矩阵。以元素组Cj的元素ejl (l=1,2，…，n)为准则，构造判断矩阵，将元素组Ci中的各元素与ejl的重要度进行比较。通过一致性检验，即得到网络元素的权重向量，从而形成矩阵Wij。例如，矩阵Wij中的第一列表示Ci中各元素相对于Cj中第一个元素的重要度归一化后的结果。如果Ci和Cj之间无影响，则Wij = 0。

表 1

Excel表格中,每一个格子称为单元格,用表1中第一列的1,2,3,…表示行数,第一行A,B,C,…表示列数.例如表1中选中的是C2单元格,其内容是“0”.单元格中既可以输入数字,如单元格B2;也可以输入字符,如单元格 G1;还可以输入公式,如单元格 D2、C3等.公式的特点是以“=”号作为起始符号.就是要利用其可以利用公式作计算的功能.注意,在 Excel表格中输入公式后,将直接显示计算结果,如表2所示.若要查看某单元格公式,可以用鼠标选中后,在表中顶端 fx后的空格内查看.D2单元格的公式表示引用B2单元格的值,即为“1”.若改变B2单元格的内容,D2单元格的值也会随之变化.

还要用到自动填充功能.选中某个单元格,把鼠标移到单元格右下角方框的位置,这时鼠标会变成一个黑色的十字,按住鼠标左键向下拖动,就可以实现自动填充.表1中,第4、5行的公式,就是根据第3行的公式自动填充的.注意到,F4、F5单元格的公式中,Excel自动把F3单元格引用D3改成了引用 D4、D5;而 C3单元格的公式中,“＄B＄1”表示绝对引用,在自动填充到C4、C5单元格时,不会改变.

用C列表示时间,D列表示位置,E列表示速度,F列表示加速度.单元格 E2的公式表示式(5);D3的公式表示式(3);E3的公式表示式(4);F2的公式表示式(6);……

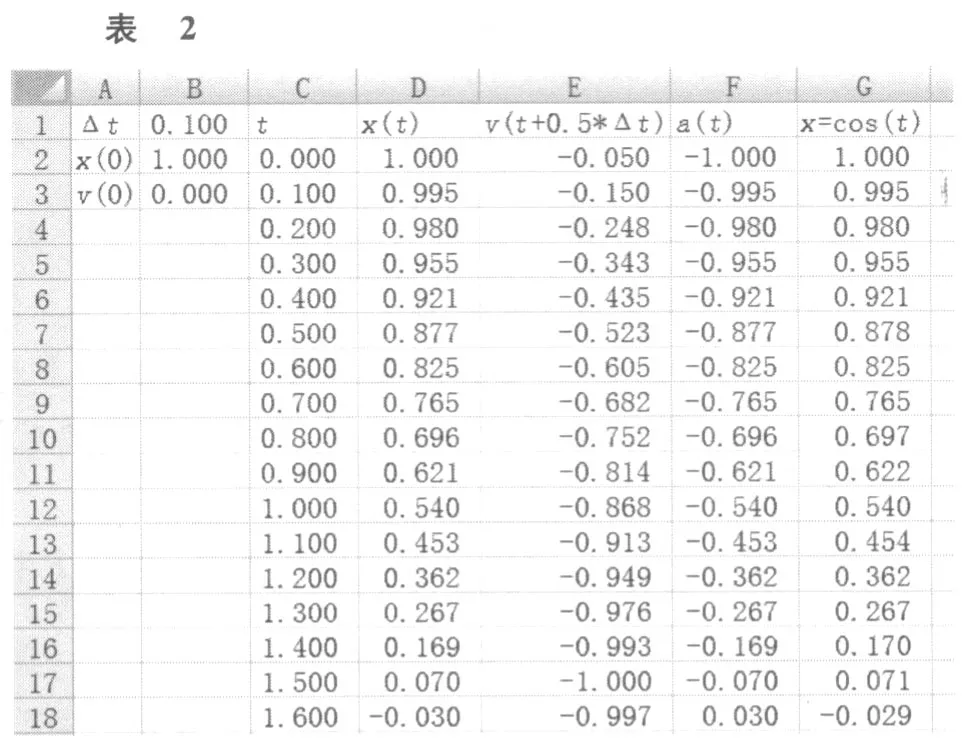
取Δt=0.100作计算,所有的结果都保留到小数点后三位.结果如表2所示.

?

最后一列是完全准确的解析解.可以做一个比较,我们发现仅在小数点后第三位上偶有一个单位的差别.

利用 Excel的作图功能,我们可以作出 x-t图.用鼠标左键依次点击插入、图表、XY散点图,选择第一类散点图,根据提示,将C列作为横坐标,D列作为纵坐标,所得 x-t图如图1所示.

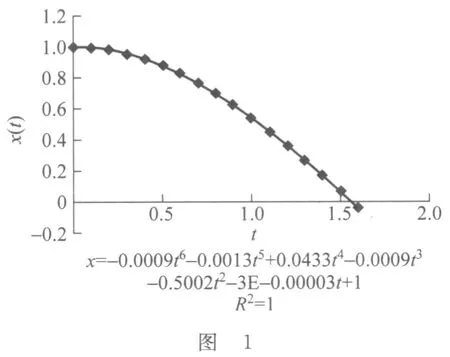
利用 Excel的添加趋势线功能,作曲线多项式拟合,并给出拟合公式.可以看出结果和精确解

可以改变初始位置(单元格B2)和初始速度(单元格B3),改变时间间隔(单元格B1),其他所有的计算结果会自动改变.例如在B2中输入“0”,B3中输入“1”,则 x-t图就会自动变成正弦曲线.这相当于在做“数学实验”.

4 行星的运动

再来看恒星系中行星的运动.假设 GM=1,行星的质量比恒星小很多,可以认为恒星是不动的,以恒星为原点,建立直角坐标系,有矢量方程

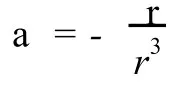
写成分量形式

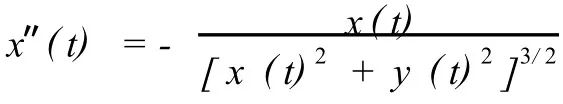
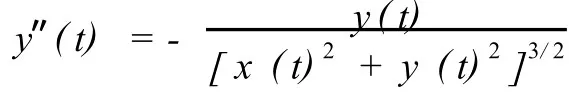
取行星的初始位置为(0.5,0),初始速度为(0,1.63),取Δt=0.100.

在Excel中的输入如表3所示.所得结果如表4所示.同样可以做出 x-y图,如图2.

?

?

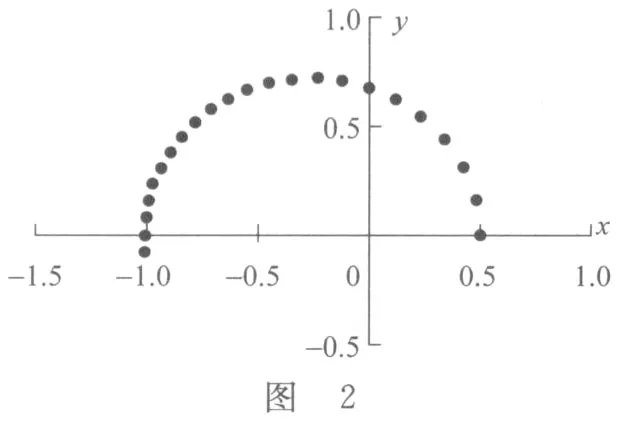
大致可以看出,运动轨迹是椭圆,原点即恒星所在位置是焦点.每个点表示相等时间间隔行星的位置,所以越稀表示速度越快,越密表示速度越慢.开始时运动较快,到末尾时运动较慢.还可计算周期、长轴、偏心率等.

有了 Excel作数值计算这一工具,还可以研究更复杂的情况.

5 双星系统的运动

考虑一个双星系统,其中一颗恒星A的质量M是另一颗恒星B的两倍.假设 GM=1;恒星A的初始位置为(-0.167,0),初始速度为(0,-0.543);恒星B的初始位置为(0.334,0),初始速度为(0,1.086).取以上数值,是为了保证双星系统的质心在原点,并保持不动;恒星B相对于恒星A的初始位置和初始速度与前面讨论的情况相同,以便比较.取Δt=0.010作计算.经过 Excel表格计算所得结果如图3所示,系列1表示恒星A,系列2表示恒星B.可以看出,双星各自绕它们共同的质心作椭圆运动[3].

图3

将在质心系中B的位置减去A的位置,并作出 y-x图,如图4所示.此即跟随恒星 A,看到的恒星B的运动的情况.可以看出恒星B绕恒星A作椭圆运动,但是周期、长轴、偏心率均有变化.

图4

6 限制性三体问题

再来考虑“限制性三体问题”[3].以上的双星系统中,另有一颗宇宙尘埃,假设尘埃的质量很小,不会影响双星的运动,考察宇宙尘埃在这两个恒星的引力场中的运动,此即“限制性三体问题”.三体问题是没有解析解的,限制性三体问题中的宇宙尘埃的运动具有混沌特性.我们可以利用Excel表格计算每个时刻宇宙尘埃的位置,画出y-x图,体会混沌运动的特点.

取尘埃不同的初始位置、初始速度,不同的时间间隔,Excel表格计算所得结果如图5所示.图中系列3表示宇宙尘埃位置.

图5

综合以上几个结果,可以看出,虽然尘埃运动的动力学规律是确定的,但其运动却对初始值、时间间隔相当的敏感,微小的扰动会产生极大的变化.此即混沌运动的特点.

还可以注意到尘埃经过双星附近时,速度变化明显,此为“弹弓”效应[4].

7 结论

数值计算的思路简单明了,可用于求解运动方程、计算积分等,有助于理解物理知识,随着计算机普及,学生利用计算机的能力提高,在大学物理课程中推广利用 Excel作数值计算,学生能够也乐于接受.

[1] [美]费恩曼等著.费恩曼物理学讲义(第一卷)[M].郑永令等译.上海:上海科技出版社,2005.95～101

[2] [美]John Walkenbach著.Execl公式与函数应用宝典[M].邱燕明等译.北京:电子工业出版社,2004.21～38

[3] 赵凯华,罗蔚茵.新概念物理教程力学[M].北京:高等教育出版社,2004.275～278,326～329

[4] 张三慧编著.大学物理学 力学、热学[M].北京:清华大学出版社,2008.135～137

2010-09-06)