量子密码及BB84协议的分析

翟晨曦 郑心如 杨建伟

(东南大学吴健雄学院610081班,江苏南京 211189)

量子密码及BB84协议的分析

翟晨曦 郑心如 杨建伟

(东南大学吴健雄学院610081班,江苏南京 211189)

拥有强大破密功能的量子计算机的出现预示着传统的RSA密码算法最终将被淘汰.要对付量子计算机惊人的密码破译功能,唯一途径就是运用量子密码技术.作为量子密码术中最基本的协议,BB84协议有其独特的优势.尽管我们是一年级学生,但在《双语物理导论》课程教育理念的鼓励下,带着对量子密码的兴趣,我们小组展开了对它的初步研究,阐述了量子密码学原理及BB84协议,并就此分析了其安全性及制约因素.

量子密码原理;BB84协议;安全性;制约因素

1 量子密码学原理

微观世界的粒子有许多共轭量,如位置和速度、时间和能量,都是一对共轭量,在某一时刻,人们只能对一对共轭量之一进行测量,不能同时测得另一个与之共轭的量,比如对位置进行测量的同时,就失去了对速度进行测量的可能性.

海森堡量子测不准原理:对于任意两个量子的测量值 A和B,有

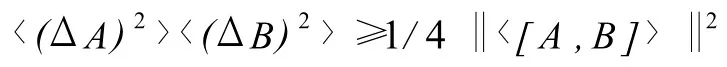
式中 ,ΔA=A-〈A〉,ΔB=B-〈B〉,[A,B]=AB-BA.

可见,(ΔA)2和(ΔB)2反映了测量值 A和B的不确定性.由于测量值存在不兼容性,即对于[A,B]≠0,测量值 A的不确定性(ΔA)2的减少将迫使测量值B的不确定性(ΔB)2增加,反之亦然,因此不可能同时准确测量A和B,对其中一个的测量将影响对另一个的测量.

在传统的物理信道中,当存在窃听者时,收发双方不会知道窃听者的存在,尤其像光盘或无线电波,其中所携带的信息在被复制或截收时都难以被发现.但当信息以量子为载体时,根据量子力学的原理,微观世界的粒子的位置不可能被确定,它总是以不同的概率存在于不同的地方.对未知状态的量子系统的每一次测量都必将改变系统原来的状态.反过来说,如果系统状态没有改变,也就没有测量或窃听行为的发生.也就是说,一个位置的量子状态不可能被复制或克隆,因此它也被称为不可克隆原理.量子密码学利用了量子的不确定性,一旦信道上有窃听发生,通信本身必然受到影响,从而达到发现窃听者的目的,保证信道的安全.

但这个密码系统的缺点是通信者只能在机密消息传送之后才能发现是否有窃听的出现,而不能在过程中察觉.因此通常在使用信道传输真正的机密消息之前,只用量子密码方法传输一个随机的密钥,来判断该信道是否安全.实际上这是为了保证通信安全的一个基本处理原则.随机密钥可以是一个随机的比特序列.这样,当消息正在传输时,窃听者通过测量量子系统的状态来读取消息时必然改变原有状态.如果通信双方发现密钥在传输过程中已受到窃听,他们就丢弃它.然后他们重新传输另一个随机密钥,直到没有窃听出现为止.

2 BB84量子密码协议

BB84量子密码协议是第一个量子密码通信协议,由Bennett和Brassard于 1984年创立.它基于两种共轭基的四态方案,用到了单光子量子信道中的测不准原理.BB84也是唯一被商业化实现的量子密钥分发协议.

BB84密钥分发协议用光子作为量子系统.光子有一个固有的称为极化的属性,一个光子或者被+基极化,或者被×基极化.假设通过一个垂直极化的滤光器发送一串光子流,则它们被垂直极化至“|”方向上.之后通过另一个极化滤光器来测量,这个用于测量的滤光器可以改变它与垂直方向的角度,只有当测量滤光器位于水平位置“—”方向时没有光子能通过它,其余角度均有光子通过.实际上,每一个光子都以一个确定的概率穿过这个测量滤光器,这个概率连续地从100%(滤光器处于垂直位置时)变化到50%(滤光器处于45°时)再变化到0%(滤光器处于水平位置时).

2.1 无噪声BB84量子密码协议

我们用单光子的极化状态来描述BB84协议,这里选择×基或+基极化编码方案(和|表示bet1,/和—表示bet0).Bennett和Brassard指出,如果Alice只用一种特定的极化编码方案与Bob进行通信,则 Eve的窃听可能不会被发现.因为Eve能100%准确地截取到Alice传输的内容,然后假装Alice重传她收到的内容给Bob,Eve所用的这种策略称为不透明窃听.

为了确保能够发现Eve的窃听行为,Alice和Bob需要进行两阶段的通信.

在第一个阶段,Alice通过量子信道单方向每次传输单个比特,每个比特对应光子的一个极化状态,她等概率地使用×基极化或+基极化两种方式.Bob只要将测量仪的极化方式设置得与发送方一致,接收正确率就是100%,否则正确接收的概率是50%.由于×基极化和+基极化的测量仪不能同时使用,对Alice所传送的每一位,Bob可以选择+基极化或×基极化进行测量,有50%的概率猜测正确.因此总体上Bob正确接收Alice传输的比特的概率是

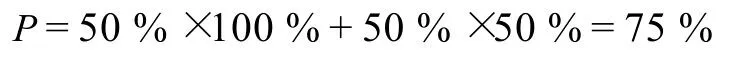
对于由Alice传输的每一比特,假定Eve窃听的概率为λ(0≤λ≤1),则不窃听的概率为1-λ.由于Bob和 Eve都是相互独立地设置测量的位置,也与Alice的设置没有联系,Eve的窃听将对Bob接收的结果产生影响,这种影响是可发现的.由于Eve的窃听使得Bob的错误接收率从25%变到

这样如果 Eve对每一位都窃听,即λ=1,则Bob接收出错的概率从25%增加到37.5%.

在第二阶段,Alice和Bob通过公共信道进行通信公开比对自己滤光器的基矢设置,再通过分析Bob的接收出错率来检查是否遭到窃听.

首先Alice和Bob要去除错误的比特.他们通过比较滤光器的基矢设置留下相同的比特部分,对于其他滤光器基矢设置不正确的比特则扔掉.这样他们分别得到各自的原密钥.如果没有入侵行为发生,则Alice和Bob的原密钥将是一致的.如果 Eve实施了窃听行为,则Alice和Bob的原密钥不一致的概率是

之后Alice和Bob通过公共信道启动一个双向会话来判断是否遭到窃听.在没有噪声的环境中,Alice和Bob的原密钥只要有不同就说明有入侵.因此要发现 Eve的入侵,Alice和Bob从原密钥中随机选择一个比特数为m的子序列进行公开比较.如果完全一致,Eve窃听但不被发现的概率是

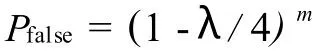
如果 Pfalse足够小,Alice和Bob可认为没有窃听出现,可将余下的原密钥作为他们最终通信的秘密密钥.如果取λ=1且 m=200,则

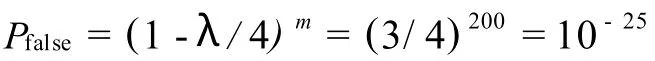
这个概率小到可以忽略.

2.2 有噪声BB84量子密码协议

实际的通信环境通常是有噪声的.这时候Alice和Bob就不能区分传输发生的错误是由噪声引起的还是由 Eve的窃听引起的.为了安全起见,他们必须假设所有错误都是由 Eve的窃听引起的.

和无噪声情形一样,整个协议工作分为两个阶段.第一阶段是基于量子信道的通信,除了错误可能由噪声引起外,其他和无噪声情况完全一致.

第二阶段Alice和Bob基于公共信道进行四个通信过程.

确定原密钥这个过程除了Alice和Bob删除那些Bob已经收到但并未接受的比特外,其余与无噪声情况完全一致,这里所说的未接受比特可能是由Eve的入侵或Bob的探测器的噪声引起的,后者称为“暗计数”,发生的位置由Bob通过公共信道告诉Alice.

原密钥错误估计Alice和Bob通过公共信道来估计原密钥中的出错率.他们公开地选定原密钥的一个随机取样并比较这些位以获得错误率的估计值 R.这些位将被从原密钥中删除.如果 R超过了一个极限值Rmax,那么Alice和Bob不可能获得最终的共享密钥,Alice和Bob只能回到第一阶段重新开始.

确定协调密钥这一步的目的是要从原密钥中清除所有的错误比特以产生一个无错误的密钥,称为协调密钥.首先,Alice和Bob协商一个随机的置换规则作用于他们各自的原密钥.接下来,Alice和Bob将原密钥分成长度为1的分组,这里选择长度1是为了保证该长度的分组不可能包含超过一位的错误.对于每一个这样的分组,Alice和Bob公开地比较整个分组的偶校验,每次要将被比较分组的最后一位丢弃.如果偶校验比较出现不一致,Alice和Bob就将这一组再分成两个子分组,对这两个子分组的每一个进行偶校验,丢弃每一个子分组的最后一位.这种操作称为双叉误差搜索.重复进行这一操作直到所有的错误比特被发现和删除,再继续处理下一个分组.

Alice和Bob随后公开地随机选取剩余原密钥的子集,公开地比较偶校验结果,每次处理所选定的密钥取样中的一位.如果一个偶校验不一致,就用双叉误差搜索来确定和删除错误位.

确定最终密钥Alice和Bob现在已有一个协调密钥,这个密钥对Eve只是部分保密的.他们要确定的最终密钥,就是从这个部分保密的密钥中抽取出来的秘密密钥.

设在误差估计为 R的情况下,Alice和Bob获取了一个n位的协调密钥,该密钥被 Eve知道的位数的上限为k.他们随后选择协调密钥的n-k-s位的子集,s是一个理想的安全参数,可由 Alice和Bob调整.他们不公布其内容及奇偶校验结果.这个保密的内容成了共享的最终密钥.可以证明Eve关于最终密钥的平均信息低于2-s/ln2位.

2.3 BB84量子密码协议实例演示

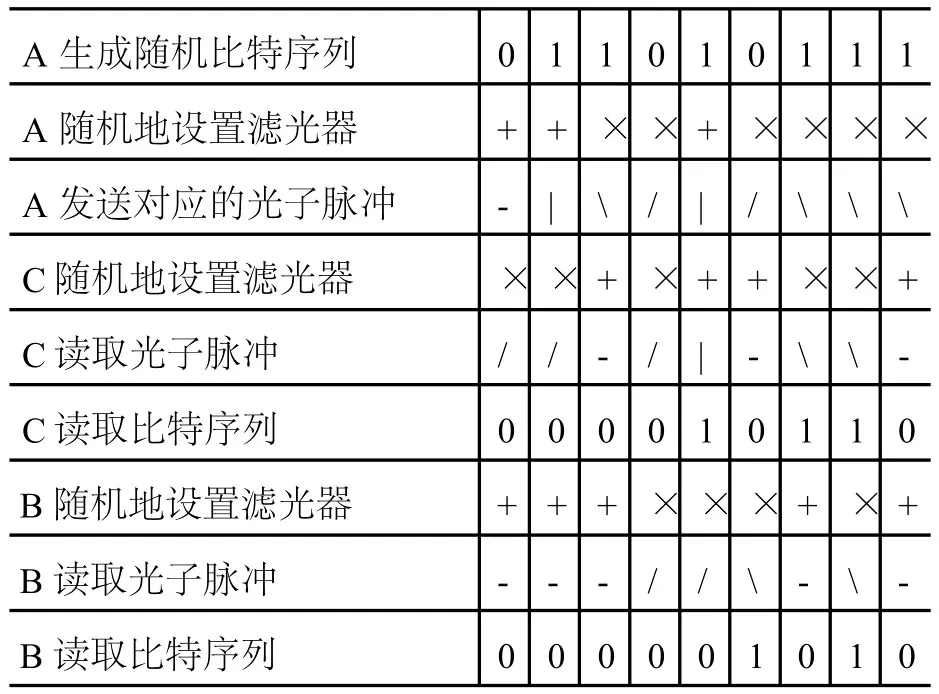
续表

3 量子密码分析

3.1 量子密码的安全性分析

量子密码的安全性分析是指被窃听但没有发现的概率.A传送一个比特,B正确接收的平均概率为3/4,因此,如果A发送 N比特,则B平均可得到3N/4个正确的比特,减去B公布的 x%用于检验的比特,实际A、B间可作为密钥共享的比特只有:3N/4(1-x%).之前说过,没有窃听时,A验证的所有比特都是正确的.当A验证的比特中出现错误时,说明一定有窃听的出现.但当A验证的所有比特都没有出现错误时,遭到窃听但没有发现的概率是多少呢?按照刚才的假设,如果B公布 x%的比特,则B需要公布3N/4×x%比特用于验证,因为每个比特被窃听而不被发现的概率为1-λ/4,而共公布的比特数为3N/4×x%,因此这些公布的比特被窃听而不被发现的概率为

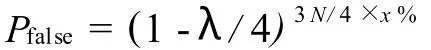
也就是说,C窃听的概率λ越高,即窃听的位数越多,A、B间发送的比特数 N越多,B公布的比特比例 x%越大,则窃听不被发现的概率 Pfalse就越小.

一般来说B公布的比特比例为1/3,即 x%=1/3,如果A、B间发送的比特数为 N,则在无窃听的情况下,A、B间所发送的比特能用作密钥共享的比特数为:3N/4(1-x%)=3N/4(1-1/3)=N/2,即实际可作为密钥共享的比特数只占发送比特的1/2,因此,如果需要得到典型的128位的密钥,则平均至少要求 N=2×128=256比特,考虑到在极端情况,即 Eve对每一位都进行窃听,此时λ=1,则窃听不被发现的概率为

由此可见,当选取的位数足够多时,C进行窃听而不被发现的概率几乎为零.所以量子密码可以抵抗拥有无穷计算能力的攻击者,这一点要大大优于现有的其他密码算法.随着计算机计算能力的不断增强,认为量子密码学是未来唯一安全的密码技术也未尝不可.

3.2 量子密码面临的制约因素

目前,阻碍量子密码术走向实用还存在一些技术问题:

首先,由于光纤具有损耗低、稳定性高以及能实现长距离传输的优点,所以可以考虑在光纤中建立量子信道,信息载体采用单光子.但问题是制造出高效地单光子源比较困难,这是因为在实际中获得理想的单光子很困难.而另一个关键问题是我们还需要有能在所需波长条件下工作的高效地单光子探测器.

我们还要防止窃听者假扮合法通信者非法获取通信信息.因此量子密码要走向实用必须结合一些经典技术,如保密加强、纠错及认证技术等.这在一定程度上也减弱了量子密码术在技术上的优势.

量子密码系统即使没有窃听者窃听,由于系统自身的不稳定性也会造成一定的长期误码率,使通信的质量受到影响.事实上在实际量子通信系统传输过程中,光探测器暗计数误码、信道噪声所产生的误码也会导致一定的误码率.

阻碍量子密码术走向实用很重要的非技术问题则是经济问题.因为量子通信技术必须与传统的通信技术来竞争以获得市场,而这些传统方法在长距离传输上以及成本费用上的优势使量子密码通信技术处于不利地位.

4 发展前景

量子密码从理论设想到现在已实现的在常规光缆线路上传输达几十千米的量子密码系统只用了短短几年的时间.如此迅速之发展足以证明量子密码技术的强大生命力.它的前途是不可估量的.在不久的将来,随着单光子探测等技术的不断发展,量子密码技术在全光网络和卫星通信等领域的应用潜力会不断成熟.量子密码已是密码学领域的一个新的成员,而且必将成为光通信网络中数据保护的有力工具.在将来要对付拥有量子计算能力的密码破译者,量子密码可能是唯一的选择.

[1] 陆果.基础物理学教程[M].北京:高等教育出版社,2008.494～497

[2] 曾贵华.量子密码学[M].北京:科学出版社,2006.256～270

[3] 马瑞霖.量子密码通信[M].北京:科学出版社,2006.42～44,56～57

[4] 胡向东,魏琴芳.应用密码学[M].北京:电子工业出版社,2006.318～325

2010-04-06;

2010-09-21)