Excel迭代功能在水力计算中的应用

乔双全，伏世红，孟祥国

(1.齐齐哈尔市水利勘测设计研究院，黑龙江齐齐哈尔 161006;2.嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔 161005)

Excel迭代功能在水力计算中的应用

乔双全1，伏世红1，孟祥国2

(1.齐齐哈尔市水利勘测设计研究院，黑龙江齐齐哈尔 161006;2.嫩江尼尔基水利水电有限责任公司，黑龙江齐齐哈尔 161005)

介绍了Excel的迭代功能，并应用于水力学公式求解，提出了直接迭代法、直接迭代加速法和隐式迭代法等3种应用Excel迭代功能进行水力计算的方法，并给出工程计算实例。

Excel;迭代;水力学;数值方法;收缩水深;求解应用

0 引言

在水力计算中经常需要求解非线性方程的根，非线性方程数值求解方法主要有迭代法、二分法等，由于计算复杂，工作量大，需要借助计算机编程加以解决。目前，水利行业水力计算软件数量少，工作中常常不能满足需要。Excel作为常见的数据分析工具，具有强大的数值处理功能。采用Excel表格形式进行水力计算，无须编程，计算过程直观明了，便于阅读和改正，非常适合专业编程人员以外的工程设计人员理解和掌握。然而，在运用Excel进行水力计算的过程中，很多工程设计人员不熟悉Excel迭代功能，而是直接列表手动试算，增加了工作量，降低了成果精度;另外，Excel只能进行显式函数关系试算，水力计算中很多公式函数关系是隐式的，很难转换为显式，不能直接利用其迭代功能进行试算。本文拟利用Excel的迭代功能，设计直观的方程迭代算法，提出了迭代的加速算法和隐式函数关系迭代的算法，满足常见的水力计算求解。

1 求解方法

使用Excel迭代计算，应首先设定迭代计算选项，Excel 2003操作方法:点击菜单工具→选项，选中重新计算选项卡，选中“迭代计算”选择框，设定最多迭代次数和迭代误差。Excel迭代计算通过调整“可变单元格”的数值，使“目标单元格”达到一个特定值，“可变单元格”最终数值即为方程的解，求解精度由最多迭代次数和迭代误差设定。

1.1 直接迭代法

当方程可用显式x=g(x)表达时，可用直接迭代法。迭代法是一种逐次逼近的方法，其基本思路就是将隐式函数方程归结为一组显式的计算公式，其过程是一个逐步显示化的过程。显式迭代很容易在Excel表格中实现，以收缩水深hc计算为例，说明直接迭代在Excel中如何实现。

收缩水深hc计算公式形式，见式(1)，将其转化为x=g(x)的显式形式，见式(2)。

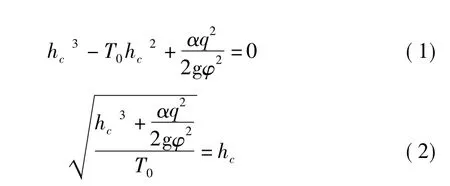
式中:T0为总势能，m;q为单宽流量，m3/(s·m);hc为收缩水深，m;α为水流动能校正系数，1.0;φ为流速系数，0.95;g为重力加速度，9.81 m/s2。

用Excel进行直接迭代计算的基本步骤和说明如下:

1)在Excel中建立如表1的新工作表，表中第1行为各个输入参数或计算公式说明单元格，第2行为输入的初始值或计算值;D1单元格g(x)代表式(2)的左边部分，H1单元格f(x)代表式(1)的左边部分。

2)在A2、B2单元格中输入参数初始值，C2单元格可输入hc试算的一个初始值，例1.00m，其余各单元格按照第1行参数说明输入相应的计算公式，计算结果列于行2。

3)将hc试算初始值改为等于迭代公式单元格，即将C2单元格等于D2，启动迭代运算，直到满足设定的最多迭代次数或迭代误差的计算要求，计算结果列于行3。

4)由表1计算成果，hc=0.793m，单元格D2等于单元格C2，单元格H2等于0，即满足式(2)和式(1)函数关系，计算成果无误。上述计算结果是在最多迭代次数为100，迭代误差为0.001情况下的成果，计算速度较快。

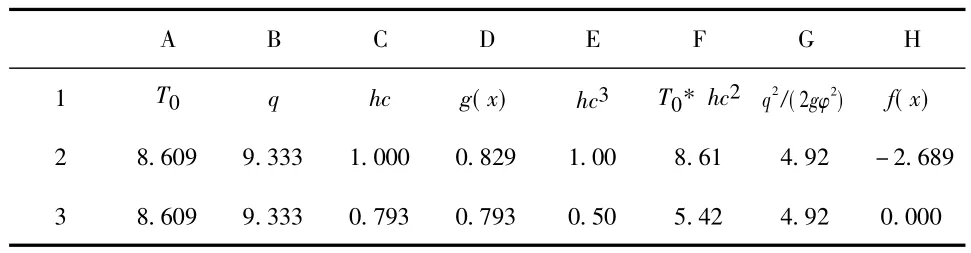
表1 直接迭代法求解收缩水深hc

1.2 直接迭代加速法

直接迭代法只要迭代足够多次，就可以使结果达到任意的精度，但有时迭代过程收敛缓慢，从而使计算量变得很大，为了提高计算效率，可以采用迭代收敛的加速法。常用迭代收敛的加速法有埃特金(Aitken)加速法和斯蒂芬森(Steffensen)迭代法等。以埃特金(Aitken)加速法为例，介绍一下在Excel中的实现方法。埃特金公式形式为:

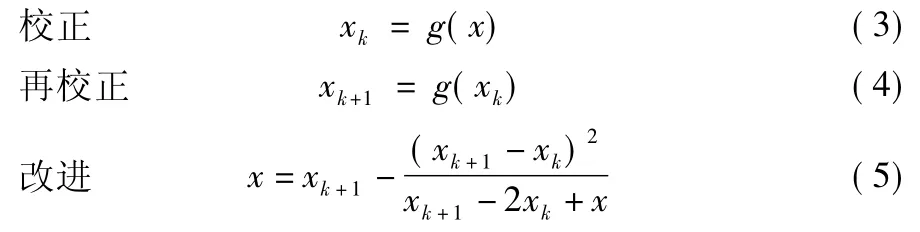
仍以收缩水深hc计算为例，埃特金加速法在原直接迭代法的基础上增加3个计算单元格:校正、再校正和改进，其他参数和单元格同表1。C2单元格可输入hc试算的一个初始值，例hc=1.00 m，计算结果列于行2。将hc试算初始值改为等于迭代公式单元格，即将C2单元格等于F2，启动迭代运算，计算结果列于行3。

由表2计算成果，hc=0.793 m，同直接迭代法，埃特金加速法加快收敛，一般迭代1～2次即可达到计算精度。

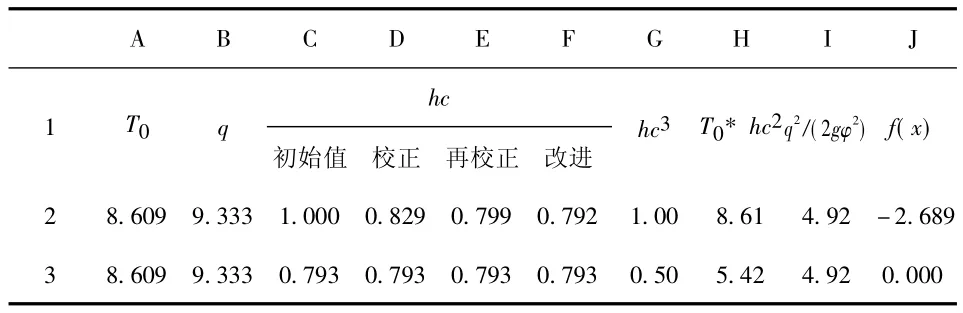
表2 直接迭代埃特金收敛加速法求解收缩水深hc

1.3 隐式迭代法

水力学中的很多公式很多难以转化为显式x=g(x)表达式，因此隐式f(x)=0求解显得更为实用。隐式迭代法主要有牛顿(Newton)法、弦截法和抛物线法等。牛顿法具有更快的收敛速度，实现简单，以牛顿(Newton)法为例，介绍一下在Excel中的实现方法。牛顿迭代法公式形式为:

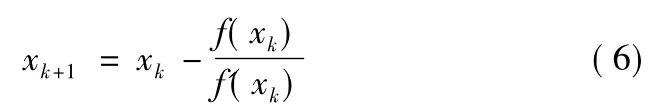
如果函数比较复杂，求导有困难，则采用差分代替导数的近似牛顿法，迭代公式为:

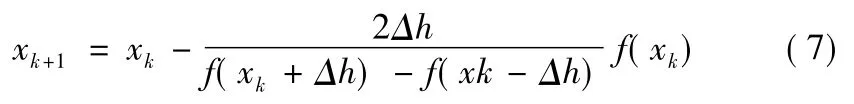
式中:Δh是数值导数的半步长，其大小需要合理选定。

以明渠均匀流正常水深h计算为例，说明牛顿法的实现方法。明渠均匀流计算公式见式(8)。

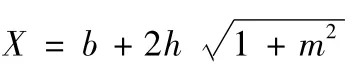
用Excel采用牛顿法进行迭代计算的基本步骤和说明如下:

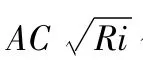
3)将h试算初始值改为等于迭代公式单元格，即将G4单元格等于H4单元格，启动迭代运算，计算结果列于表4。

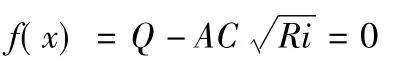
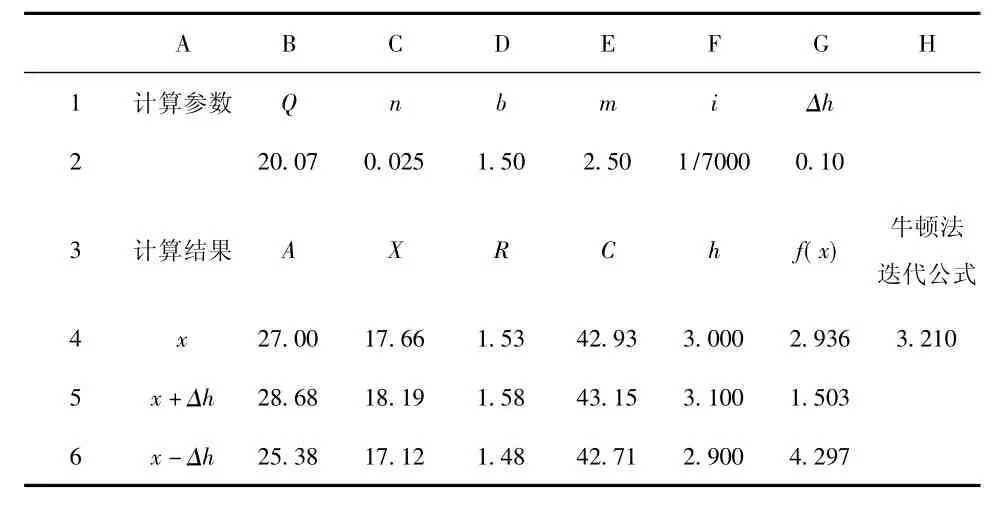
表3 牛顿迭代法求解明渠均匀流正常水深h(初始值设定)

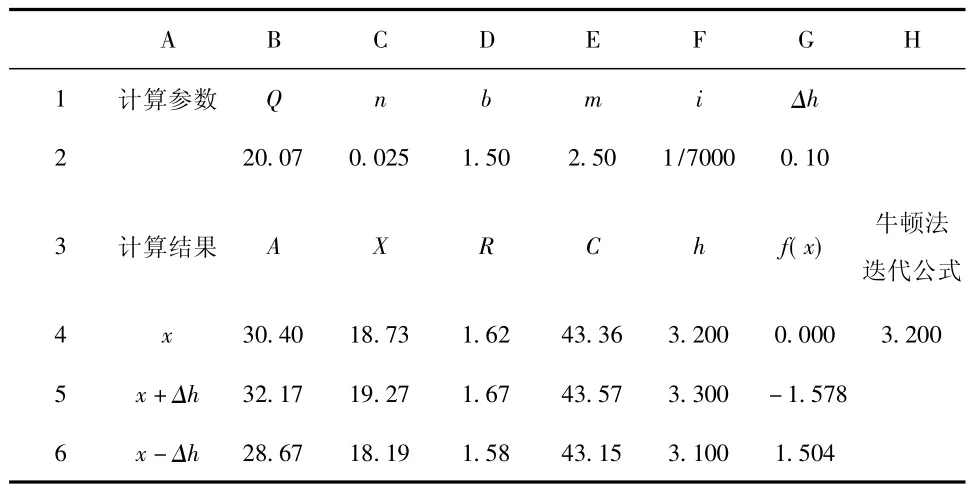
表4 牛顿迭代法求解明渠均匀流正常水深h(迭代结果)

2 结论

1)利用Excel迭代功能，可方便的实现水力学公式求解，计算过程直观，便于检查，易学掌握。用Excel迭代功能进行计算，即克服了繁琐的手工试算，又避免了编写专业的计算程序，在水力计算乃至其他计算中都值得推广、采用。

2)Excel迭代工具实际采用的是弦截法，迭代过程中可能会出现错过根值的情况，在试算时，可初估实际根值，若试算初始值小于实际根值无法得到试算结果，可将试算初始值设为大于实际根值。

3)Excel数值分析和计算功能强大，本文只涉及其迭代功能，其他尚有许多功能和技巧值得研究，如:规划求解、矩阵功能等，值得在水力计算进一步应用和开发。

［1］ 李庆扬，王能超，易大义.数值分析(第四版)［M］.北京:清华大学出版社，2001.

［2］ 李炜.水力计算手册(第二版)［K］.北京:中国水利水电出版社，2006.

［3］ 熊启钧.灌区建筑物的水力计算与结构计算［M］.北京:中国水利水电出版社，2007.

TV31

B

1007－7596(2011)05－0029－02

2011－05－12

乔双全(1974－)，男，黑龙江齐齐哈尔人，工程师;伏世红(1984－)，男，甘肃天水人，助理工程师;孟祥国(1983－)，男，吉林伊通人，助理工程师。