二维阵列亥姆霍兹共鸣管的声带隙性能
许震宇,卢 强,李 斌
(同济大学 航空航天与力学学院,上海200092)
与光子晶体类似,声子晶体是由两种或两种以上弹性材料构成的周期结构.由于具有声带隙等特性,对声子晶体的研究得到越来越多学者的关注.声子晶体的研究方向之一是如何设计能获得较大带宽的结构.常见的方法包括叠加法、多元材料法、可调法等[1-2].
亥姆霍兹共鸣器是一种最基本的声共振系统,可受外面声场的激发并消耗其能量,形成重要的吸声体结构[3].其最典型的应用就是音乐厅、电影院吸音墙的微结构[4].亥姆霍兹共鸣器有三维腔体、二维管状等结构.将亥姆霍兹共鸣管周期排列,可以形成一维或二维声子晶体结构[5-6].该结构可以形成布拉格散射效应、局域共振效应以及亥姆霍兹共鸣管对声波的吸收效应,故有可能获得更大的带宽并具有其他声学特性.Fang等人基于亥姆霍兹共鸣器一维阵列,设计了具有负模量的超材料并进行了实验验证,这种材料具有负折射率等性质[7].Zhang等人在Fang等人的工作基础上,设计了超材料声学透镜,并且通过实验证明这种结构可以将亚波长的超声波聚焦[8].可以预见,亥姆霍兹共鸣器将在新型声学器件的设计中得到更多的应用.
可以利用平面波展开法、传输矩阵法、多重散射法、有限元法、时域有限差分法等方法计算声子晶体、声学超材料等结构的声学特性[9].这些方法有各自的适用范围.例如,平面波展开法在处理声固耦合问题时,很难得到收敛的结果;多重散射法只能计算球形散射体结构的带隙性能;而时域有限差分法和有限元法具有更广泛的适用性[9].本文设计了二维的亥姆霍兹共鸣管周期阵列结构,并应用有限元方法计算该结构的声传输特性.首先介绍了亥姆霍兹共鸣管二维阵列的结构,以及有限元方法的基本原理,通过经验公式的计算结果验证了有限元法的可靠性,然后利用该方法计算了阵列结构的声透射性能.
1 结构
一个空心圆球插一根短管就构成亥姆霍兹共鸣器,短管可以只连到空球或插入球心,也可以只在空球开一个口.图1是几种亥姆霍兹共鸣器的示意图.图中,d为颈或开口的直径;l为颈的长度;V为容器的容积.
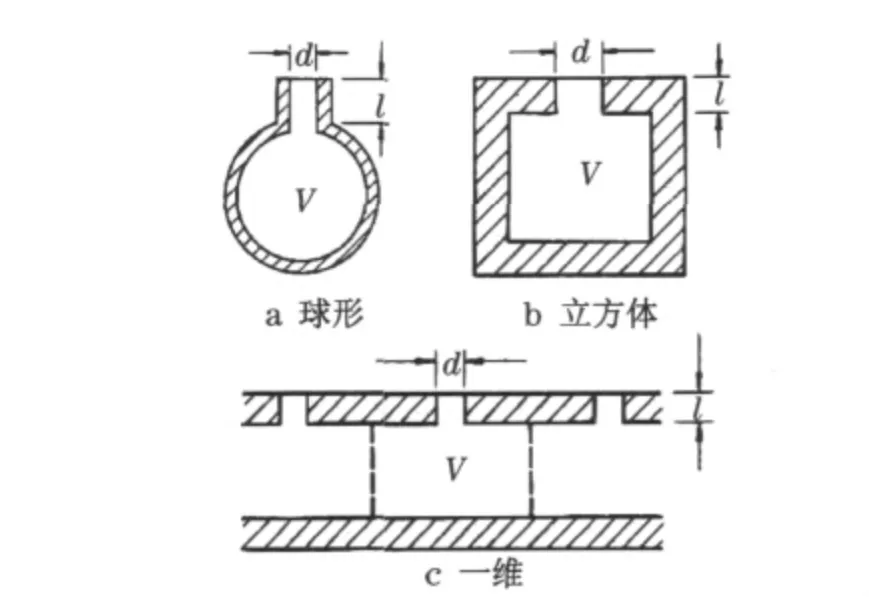
图1 亥姆霍兹共鸣器示意图Fig.1 Several examples of Helmholtz resonators
亥姆霍兹共鸣器吸声性能的特点是对频率有较强的选择性,只在某一个特有频率附近有较强的吸声作用,而在其他频率范围吸声作用很小,这个频率称为共振器的共振频率f0.图1中的几种共鸣器都有各自的共振频率.可以针对吸声的不同频率要求选择和设计不同的共鸣器形式.共振频率的计算公式为[4]

式中:c为声速(本文中均取为340m·s-1);S为颈或开口的截面积,m2.
本文的二维阵列结构的截面如图2所示.每一个亥姆霍兹共鸣管两端无限长,并在横向周期排列在空气中,形成二维阵列.其外径为2.04cm,内径为1.84cm,开口长度为2mm,排列周期为2.4cm,材质为钢材.

图2 二维的亥姆霍兹共鸣管周期阵列Fig.2 Two dimensional array of Helmholtz resonators
2 计算方法
对于无源无粘的介质,谐波响应的Helmholtz方程为
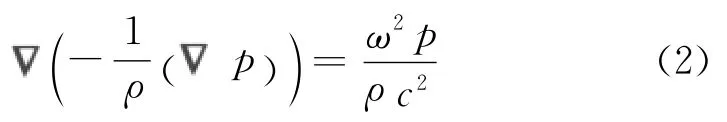
式中:p为声压,N·m-2;ρ为空气密度,kg·m-3;ω为角频率,弧度·s-1.
本文采用商用软件Comsol Multiphysics计算该方程的特征值问题,也称为频响分析.该软件是一个专业有限元数值分析软件包,是对基于偏微分方程的科学和工程问题进行建模和仿真计算的交互开发环境,可以处理任意数目的耦合问题.对于声学问题,该软件可以处理的边界条件包括:刚性;柔性;声源;指定法向加速度;阻抗;辐射等.本文中,将共鸣器或二维阵列围在矩形的计算区域中,并划分网格.由于与结构相比空气的密度较低,所以将结构视为刚体,结构与空气的边界应用刚性边界条件.矩形计算区域的一条边为入射声源,设置为幅值为1的谐波.其他三条边使用了辐射边界条件以模拟无反射边界.计算过程中,取空气密度为1.29 kg·m-3,声速为340m·s-1.将入射波的频率在一定范围内取值,即可以计算得到该频率透射波的声压衰减值.
为了验证有限元方法的可靠性,考察图1a所示结构的共振频率.其中,颈的直径d为2cm,颈的长度l为10cm,球腔的容积V为2.2dm3.图3显示了利用频响分析得到的图1a所示结构的频响曲线.可以看出在58 Hz结构有共振现象.利用式(1)的计算结果为60Hz,两者相符.所以,可将该方法用于计算结构的频响特性.

图3 单个亥姆霍兹共鸣器的频响曲线Fig.3 Frequency response of one Helmholtz resonator
3 结果
对于图2所示的声子晶体结构,可以计算得到其(100)方向的透射性能,如图4a所示.注意到,在5 500Hz到9 500 Hz有一个较宽的带隙.图4b显示了完整二维周期结构(由无开口管周期排列构成)的计算结果.其带隙出现在6 500Hz到9 500Hz范围内.两者相比,图4a中的该带隙更向低频扩展.同时,在所考察的频率范围内二维亥姆霍兹共鸣管周期阵列在2 000Hz到3 000Hz还出现了新的带隙.所以,在结构总体尺寸相同的情况下,二维亥姆霍兹共鸣管周期阵列可以禁止频带更宽并且频率更低声波的通过.

图4 两种结构声透射性能的比较Fig.4 Sound transmission of two structures
为了考察声波入射方向对声带隙的影响,计算了声波不同入射方向下,结构的频响特性.图5 是(010)方向入射波的频响曲线.可以看出,不同传播方向上的声带隙位置、宽度基本相同.
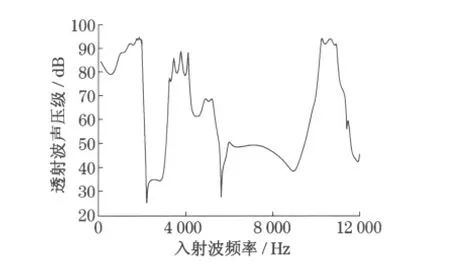
图5 (010)方向入射波的频响曲线Fig.5 Frequency response with the(010)incident wave
如果将亥姆霍兹共鸣管的位置不变,而开口方向随机排列,可计算其频响曲线如图6所示.可见其声带隙位置和宽度与规则排列相比,差别也很小.说明声波在结构中传播时存在局域共振效应.
如果将亥姆霍兹共鸣管的位置和开口方向都随机排列,可计算其频响曲线如图7所示.可见其声带隙位置和宽度与规则排列相比,差别仍然很小.比较图4~图7,可知在2 000Hz附近的带隙应该是由于开口的存在造成的,并且其位置和带宽与开口的方向和散射体的位置无关.也就是说,频率在2 000Hz附近的声波在亥姆霍兹共鸣管中共振而不继续传播,从而形成带隙.这也是局域共振型声子晶体的典型特征.

图6 开口方向随机排列结构的声透射性能Fig.6 Transmission property with the random directions openings

图7 开口方向和散射体位置随机排列结构的声透射性能Fig.7 Transmission property with the random directions openings and random positions of scatterers
4 结论
二维亥姆霍兹共鸣管周期阵列作为一种新的声子晶体结构,其声带隙性能与完整二维周期结构相比,有很大的不同.由于具有布拉格散射效应、局域共振效应以及亥姆霍兹共鸣管对声波的吸收效应等综合效应,二维亥姆霍兹共鸣管周期阵列可以禁止更低频声波的通过.进一步可以考察其他类型共鸣管构成的周期阵列,优化亥姆霍兹共鸣管的结构和尺寸.还可以在此基础上设计声屏障、声透镜等其他具有独特功能的声学器件.
[1] 华佳,张舒,程建春.三元周期结构声禁带形成机理[J].物理学报,2005,54(3):1261.HUA Jia,ZHANG Shu,CHENG Jianchun.Mechanism of broad acoustic band-gap in the three-component composite[J].Acta Physica Sinica.2005,54(3):1261.
[2] Wang Y Z,Li F M.Tuning of band gaps for a two-dimensional piezoelectric phononic crystal with a rectangular lattice[J].Acta Mechanica Sinica,2009,1:65.
[3] 马大猷.亥姆霍兹共鸣器[J].声学技术,2002,21(1):2.MA Dayou.Helmholtz resonator[J].Technical Acoustics,2002,21(1):2.
[4] 王峥,项端祈,陈金京,等.建筑声学材料与结构[M].北京,机械工业出版社,2006.WANG Zheng,XIANG Duanqi,CHEN Jinjing,et al.The architectural acoustical materials and structures[M].Beijing:China Machine Press,2006.
[5] Hu X H,Chan C T.Two-dimensional sonic crystals with Helmholtz resonators[J].Physical Review E,2005,71:055601.
[6] Wang Zhiguo,Sam Hyeon Lee.Acoustic wave propagation in one-dimensional phononic crystals containing Helmholtz resonators[J].Journal of Applied Physics,2008,103:064907.
[7] Fang N,Xi Dongjuan,Xu Jianyi,et al.Ultrasonic metamaterials with negative modulus[J].Nature Materials,2006,5:452.
[8] Zhang Shu,Yin Leilei,Fang N.Focusing ultrasound with acoustic metamaterial network[J].Physical Review Letters,2009,102:194301.
[9] Garcia-Pablos D,Sigalas MM,Gacia N.Theory and experiments on elastic band gaps[J].Physical Review Letters,2000,84(19):4349.

