1∶5滚动实验台轮轨力连续测量系统
任利惠,黄 磊,周劲松,潘建壮
(同济大学 铁道与城市轨道交通研究院,上海201804)
轮轨作用力是评价铁道车辆运行安全性的主要指标.实现轮轨力的精确、连续测量是评价车辆安全性的关键技术.测力轮对是目前最直接、最准确的轮轨力测量技术,它以轮对作为轮轨力的检测传感器,通过测量轮对上有限点处的应变实现轮轨作用力的连续检测.
实物轮对的轮轨力连续测量技术主要有以下几种:①轴测法[1]——通过测量车轴轴身、轴肩几个断面上弯矩间接计算出轮轨力;②辐条轮法——采用特殊的辐条车轮来制作测力轮对;③幅板车轮法——通过在车轮几个半径上的合理组桥来尽量消除车轮转动的影响,然后求解多个非线性方程组而得到横向力、垂向力以及轮轨作用点位置[2-4].最近还出现了根据车轮横向变形测量轮轨横向力的方法[5].
上述轮轨力的测量方法都是针对1∶1 的实物车轮开发的.与实物车轮相比,小比例轮对的应变输出很小,应变片的粘帖位置和数量受到很大限制,因此无法直接套用上述方法.本文根据我校1∶5铁道车辆滚动实验台的特点,研制了小比例测力轮对,开发了小比例滚动台的轮轨力连续测量系统.
1 1∶5铁道车辆滚动实验台
我校的1∶5铁道车辆滚动实验台(图1)是针对车辆工程专业教学而开发的实验装置.实验台由4个轨道轮、驱动电机和传动系统组成.电机通过传动系统带动轨道轮转动,轨道轮再带动车辆轮对转动,以模拟车辆在直线轨道的运动,轨距287 mm.车辆为1∶5小比例整车模型,由一个钢结构车体和两台两轴转向架组成,转向架采用两级弹性悬挂,轴距500mm,车轮直径168mm.

图1 同济大学的1∶5铁道车辆滚动实验台Fig.1 1∶5th scale railway roller rig in Tongji University
为了提高测量精度,对原设计的整体幅板式车轮进行了部分改造,减少幅板厚度,增加了幅板长度,用来增大车轮上的应力.为了安装集流环,在车轴开通孔,同时轮对内侧的轴身上钻孔,以便于导线穿过.
2 测点位置选择
用测力轮对测量轮轨力,就是根据车轮上的应变还原出轮对所受的轮轨力,车轮的应变一般靠粘贴应变片来获得,因此应变的测量位置对测试结果有着直接影响.
应变测点位置的选择应遵循两个原则:①测点应有足够大的应变输出;②车轮旋转一周时,测点的输出波形要接近余弦波或三角波,以便于组桥.如果测点的输出对横向力和垂向力能够解耦,则便于方程求解.
2.1 有限元分析
测点位置的选择先借助于有限元法分析,得到轮对在垂向力和横向力作用下的应力分布.计算结果显示,车轮幅板在横向力作用下的应变远大于在垂向力下的应变,且靠近轮毂处幅板的应变最大;车轴在横向、垂向载荷的应变均较大,且在两轮之间的车轴应力最大,并呈等应变分布.
2.2 实验分析
为了进一步确定测点位置,测试了车轴和车轮幅板在垂向力、横向力作用下的应力.应变片粘帖位置和测点编号见图2,其中测点3~5反映车轮辐板上的径向应变,而测点2反映了车轴上的轴向应变.
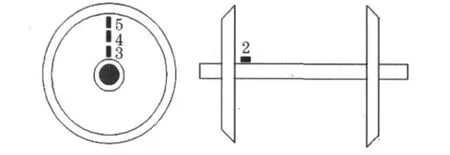
图2 小比例轮对的应力测试位置Fig.2 Stress measuring positions on 1∶5th scale wheelset
将贴好应变片的轮对分别放在垂向标定台和横向标定台上进行加载,每隔15°加载一点.数据处理时,将应力换算成1kN 的轮轨垂向或横向作用下的输出.应力测试结果见图3和图4.垂向加载时,车轮测点的应力都很小,测点3处的应力最大只有11.4 MPa.车轴上测点2的最大应力为28.8 MPa.考虑到小比例车辆的实际质量很小(空车约180kg),可以推断车轮上各测点的实际应力输出很小,而车轴上测点的应力输出适合垂向力测试.

图3 垂向载荷下各测点的应力Fig.3 Stresses of 1∶5th scale wheelset under vertical load

图4 横向载荷下各测点的应力Fig.4 Stresses of 1∶5th scale wheelset under lateral load
横向加载时,车轴测点的应力幅值为64.7 MPa,车轮上测点3应力幅值最大,为81.4 MPa,均满足横向力的测量要求.测点3在横向载荷作用下的应力远远大于垂向载荷下的应力,在同值载荷作用下,前者是后者7.2倍.
对测点应力波形进行谐波分析.测点2 在垂向力下应力波形的一阶谐波成分占90.9%,接近余弦波.测点3 在横向力下应力波形的一阶谐波占86.3%,接近三角波.
综上所述,车轴上各处均可根据需要作为应变测点,而车轮上的测点3可作为轮轨横向力测点.
3 轮轨力测量方案
小比例滚动台的轮轨力测量综合采用了车轮力法和车轴力法:轮轨横向力采用轮测法测量,再结合轴测法测量轮轨垂向力.
3.1 横向力
由于车轮幅板测点3在横向力下的输出是垂向力下输出的7.2倍,因此可以忽略垂向力对测点3的应力影响,认为测点3的输出全部是横向力作用的结果,通过组桥,能够进一步放大横向力的输出和减小垂向力的输出.
由测点3的波形特点,可以在车轮上粘帖应变片,组成余弦桥测量轮轨横向力.作为对比,在另一侧车轮贴片组成直流桥,也用来测量横向轮轨力.
3.1.1 余弦桥
如果车轮上同一半径上的两个电桥输出ε1,ε2仅与轮轨横向力Q相关时,有:

式中:k1为电桥的标定系数;f1(θ)和f2(θ)为归一化的车轮转角函数.
当车轮上应变输出接近三角波时,可以通过合理组桥使整个桥路的输出充分接近于余弦波,即使f1(θ)=f2(θ)=cosθ.在角度相隔90°的相同位置布置两组一样的测点,则方程(1)可方便地求解:

对于余弦桥法测得的横向力,可以在数据处理中得到其方向信息.其原则如下:
(1)由于车轮只可能受压不可能受拉,所以测量的垂向力P不可能为负,P为负时说明测量的横向力Q方向反向.
(2)小比例轮对与轨道轮只能产生轮缘接触而没有轮背接触,因此Q的突变只可能向内侧突变而不可能向外侧突变.
余弦桥法的关键是如何在车轮上布置应变片和组桥,使得桥路具有余弦函数的输出特性.当车轮径向应变的反对称分量使用0°,60°的简易桥时,能够消除三阶谐波分量,使得电桥的输出足够接近函数;当使用0°,36°,60°,96°的优选桥时,可消除三次谐波和五次谐波的影响,使电桥的输出非常接近余弦函数[2].由于小比例轮对幅板很小,无法布置下优选桥,只能选择0°,60°的简易桥.简易余弦桥的贴片位置和组桥方法如图5所示.

图5 简易余弦桥的贴片位置和组桥方法Fig.5 Simple cosine bridge arrangement and its strain gauges distribution on wheel plate
3.1.2 直流桥
作为对比,在另一侧车轮组成直流桥.这时,在车轮上每隔45°贴片,0°,45°,90°,135°位于电桥的一个边,其对边则为180°,225°,270°,315°,组桥方法见图6.直流桥可以直接得到横向力的大小和方向,但直流桥是一种相对测量法,由于电桥预平衡的缘故,不能获得静态的横向力.通常采用低速运行时测得的横向力作为静态值.

图6 直流桥的贴片组桥方法Fig.6 Direct current bridge arrangement and its strain gauges distribution on wheel plate
3.2 垂向力
轴测法通常需要测出车轴轴身、轴肩处6 个断面的弯矩,从而计算出作用在车轮上的轮轨力.如果在测得车轮上的横向力,则只需要通过测量车轴A,B,C,D断面的弯矩(图7),即可解得轮轨垂向力.图7中:P1,Q1分别为左轮轨的垂向力和横向力(余弦桥);P2,Q2分别为右轮轨的垂向力和横向力(直流桥);P′1,P′2分别为来自左、右一系悬挂的垂直方向作用力;H1,H2分别为来自左、右悬挂的水平方向作用力;b2~b5为车轴上测点断面至轮对中心的距离;bA1,bA2分别为轮轨接触点至轮对中心距离;r1,r2分别为左、右车轮半径.

图7 轮轨垂向力的测量原理Fig.7 Measuring method for vertical wheel/rail force
根据轮对的受力分析可得轮轨垂向力:

式(3)~(4)中,Mi为车轴i断面的弯矩,i=A,B,C,D.
4 轮轨力测试系统
4.1 测力轮对
按第3节所述的组桥方案,在一侧车轮辐板内侧粘帖应变片,组成余弦简易桥(简称余弦桥),在另一侧车轮辐板内侧粘帖应变片组成直流桥.在车轴的A,B,C,D断面沿轴向粘帖应变片,分别布置两组半桥,两半桥相隔90°.组桥后的测力轮对实物如图8所示.

图8 小比例测力轮对Fig.8 Prototype of 1∶5th scale instrumented wheelset
将组好桥的轮对分别放在垂向标定台和横向标定台进行标定,得到各测量电桥的垂向和横向标定曲线,图9给出了余弦桥和直流桥的横向力标定曲线.标定结果显示:车轴上所有断面的电桥输出数值基本相同,各电桥波形都呈余弦波;横向力作用下,余弦0°桥和90°桥的一阶谐波分量分别达到93.1%和94.0%,很接近余弦波;直流桥的输出基本呈直流特性,但直流桥的输出很小,在相同的激励电压下,直流桥的输出仅有余弦桥的1/10 左右,这说明余弦桥的测量精度远高于直流桥.

图9 余弦桥和直流桥的标定曲线Fig.9 Calibration curves of simple cosine and direct current measuring bridge
图10给出了两个余弦桥分别在等值垂向、横向载荷作用下按式(2)的合成输出.可见,横向载荷作用下的输出远远大于垂向载荷的输出,前者是后者的12.5倍之多,完全可以忽略垂向力的影响,认为其输出完全是横向力的作用.通过组桥,使得电桥对横向力的输出与对垂向力的输出之比变大了.

图10 余弦桥在垂向、横向载荷下的输出对比Fig.10 Output comparison of simple cosine measuring bridge under vertical or lateral load
4.2 系统误差
静态加载条件下,测试系统的测量误差如图11所示.可见,余弦桥的误差在±8%之内,其测量精度是可以接受的;而直流桥的误差波动最大达到了±20%左右,显然直流桥的测量精度较低,这是由于应变输出中的直流成份太小造成的.

图11 余弦桥和直流桥的误差Fig.11 Error curves of simple cosine and direct current measuring bridge
4.3 测试系统
测试系统采用虚拟仪器概念构建,主要由信号调理设备SCXI-1532 和数据采集卡PCI-6024E 组成,如图12 所示.数据采集和处理程序使用LabVIEW7.0编制.

图12 1∶5滚动台轮轨力测试系统示意图Fig.12 Diagram of wheel/rail forces continuously measuring system for 1∶5th scale roller rig
5 1∶5滚动实验台轮轨力测试
5.1 实验结果
将测力轮对装在1∶5滚动实验台上.在静态下调平仪器,滚动台开始滚动后记录实验数据,每次实验先让小车平稳运行一小段时间,这时得到的轮轨作用力可作为静态值.
实验数据的处理过程如下.
①首先对数据进行低通滤波.低通滤波截止频率取决于轮对的最低阶模态频率,这里取为95 Hz;②静态数据补偿.由于仪器在调平时,不仅消除电路的初值,同时也减掉了静态轮轨力,因此需要对测量数据进行补偿;③由交流桥和直流桥的输出得到车轮上的横向力;④求车轴各断面弯矩,它是车轴各断面0°和90°电桥输出的平方根;⑤根据式(3),(4)求得轮轨垂向力.
图13给出了重车状态下测得的轮轨作用力,图14给出了左、右车轮的脱轨系数.余弦桥侧车轮的脱轨系数变化较为缓慢,直流桥侧车轮的脱轨系数变化幅值较大,这是由于直流桥的输出误差较大造成的.

图13 1∶5滚动实验台上测得的轮轨作用力Fig.13 Measured wheel/rail forces on 1∶5th scale roller rig with instrumented wheelset

图14 小比例车辆的脱轨系数Fig.14 Derailment coefficients of 1∶5th scale rolling stock
空车时,由轮轨力测量系统测得的余弦桥侧车轮静载荷为251.9N,直流桥侧车轮静载荷为298.4 N.小比例货车空车时每个车轮的静载荷约为225 N[6].由此也证实,由余弦桥侧桥路测量的垂向力精度较高,直流桥侧的测量精度较低.
5.2 桥路的比较
余弦桥的优点是:测点输出大,测量精度高;余弦桥为绝对测量,可测量出静态轮轨力.余弦桥的缺点是:横向力的方向丢失,需其他方法确定横向力的方向.
直流桥的优点是:直接输出横向力,且带有方向信息.直流桥的缺点是:测点输出小,测量精度低;直流桥为相对测量,需要其他措施才能测量出静态横向力.
从实验结果上看,余弦桥更适合在小比例车轮上使用.
6 结束语
本文针对我校1∶5小比例滚动实验台,开发了轮轨力连续测量系统.
通过有限元分析和实验确定了应变测点的位置.车轮上的最佳贴片位置在辐板靠近轮毂处,此处对横向载荷的应变远大于对垂向载荷的应变.车轴与车轮交汇处是车轴上的最佳贴片位置.
根据应变特点,提出车轮力法和轴测法相结合的轮轨力测量方案,即轮轨横向力使用轮测法进行测量,然后结合轴测法得到轮轨垂向力.静态试验结果表明,余弦桥法测量轮轨横向力精度较高,比直流桥更适合测量小比例轮对的轮轨力.最后使用上述测试系统测量了1∶5滚动台的轮轨作用力.实践证实,车轮力法和轴测法相结合测量轮轨力是可行的.
目前该测量系统应用于我校相关课程的实践教学.
[1] Hertber H.Determination of wheel/rail forces by means of measuring wheelsets on Deutsche Bundesbahn [C ]//International Conference of Wheel/rail Load and Displacement Measure Techniques.Cambridge: Transportation Systems Center,MIT,1981(1):19-21.
[2] 曾宇清,王卫东,甘敦文,等.测力轮对连续测量的理论与实践[J].铁道学报,1998,20(6):28.ZENG Yuqing,WANG Weidong,GAN Dunwen,et al.Theory of high accuracy load measuring wheelset[J].Journal of the China Railway Society,1998,20(6):28.
[3] Kanehara H,Fujioka T.Measuring rail/wheel contact points of running railway vehicles[J].Wear,2002,253(2):275.
[4] 陈建政,王志强.轮轨接触点的在线连续测量[J].中国铁道科学,2007,28(5):15.CHEN Jianzheng, WANG Zhiqiang. On-rail continuous measurement of wheel/rail contact point[J].China Railway Science,2007,28(5):15.
[5] Matsumot A,Sato Y,Ohno H,et al.A new measuring method of wheel-rail contact forces and related considerations[J].Wear,2008,265(10):1518.
[6] 黄磊.1∶5滚动实验台轮轨力连续测量技术研究[D].上海:同济大学铁道与城市轨道交通研究院,2010.HUANG Lei. Wheel/Rail interaction forces continuously measuring system for 1∶5th scale roller rig[D].Shanghai:Tongji University.Institute of Railway & Urban Rail Transit,2010.

