哈林图的防火问题*
岳绪彬, 王维凡
(浙江师范大学数理与信息工程学院,浙江金华 321004)
设 G是一个连通图,V(G)和 E(G)分别表示 G的顶点集合和边集合.令 n表示图 G的顶点数,有时记 n=|G|=|V(G)|.设 v∈V(G),且 k≥1是一个整数.k-防火问题叙述如下:火开始在顶点 v处燃起,一个消防员可以选择 k个没有起火的顶点加以防护 (等价地,有 k个消防员每人每次保护 1个顶点),消防员和火源在图 G上交替移动.假设一旦一个顶点已经被消防员防护下来,那么在接下来火源的传播过程中,它一直是受保护的.当消防员移动后,起火的顶点将使那些没有被防护的邻点起火.当火源没法再传播时,整个过程就结束了.消防员的任务是防护尽可能多的顶点,也就是当这个过程结束时没有被烧的顶点尽可能地多.用 snk(v)表示当 v为火源时,k-防火过程中消防员救下的最多顶点个数.图 G的k-存活率ρk(G)定义为 G的顶点随机起火时 k-防火过程可救下的顶点的平均存活率,即

文献[1]首先引入了图的存活率的概念,并对树、外可平面图和哈林图等特殊图类研究了单人防火问题,即证明了以下结果:

最近,文献[2]应用概率方法证明了几乎所有图 G都有ρk(G)→0(当 G的点数逐渐增加时).此外,文献[2]还证明了以下一些结果:

关于图的防火问题的其他结果可参考文献[3-5].
一个哈林图定义为 H=T∪C,其中 T是被嵌入欧几里得平面的一棵树,T中没有 2度点且至少有一个度大于等于 3的顶点,C是依照 T的嵌入顺次连接 T的所有叶点所得到的圈.称 T是 H的特征树,C为 H的外圈.显然,H是 3-连通的平面图.关于哈林图的结构性质和相关参数见文献[6-8].
本文考虑哈林图的 2-防火问题,即证明 n-点哈林图 H满
引理 1 设 H=T∪C是一个哈林图.若 P为 T中有 k(≥2)个顶点的一条路,则 sn2(P)>(k-2)n.
证明 假设 P=v1v2…vk,k≥2,那么 T-E(P)是一个森林.对 1≤i≤k,设 Ti表示 T-E(P)中唯一包含 vi的分支,且令 ti=|Ti|.对 2≤i≤k-1,设 Tl(i)和 Tr(i)分别表示 Ti在路 P的左侧和右侧部分,亦即Ti=Tl(i)∪Tr(i)且 Tl(i)∩Tr(i)={vi}.设 C=y0y1…ym-1y0是 H的外圈,其中 m≥3,且假定 C的方向是顺时针的.由哈林图的定义,存在 C中的子路Q=yiyi+1…yj使得 V(Q)是 T1的所有叶子的集合,这里下标取模 m.称 yi是 T1的最后面的叶子 (依顺时针方向在 C上),yj是 T1的最前面的叶子 (依顺时针方向在 C上),2,3,…,k-2},能够定义 Td在 C上的最后面的和最前
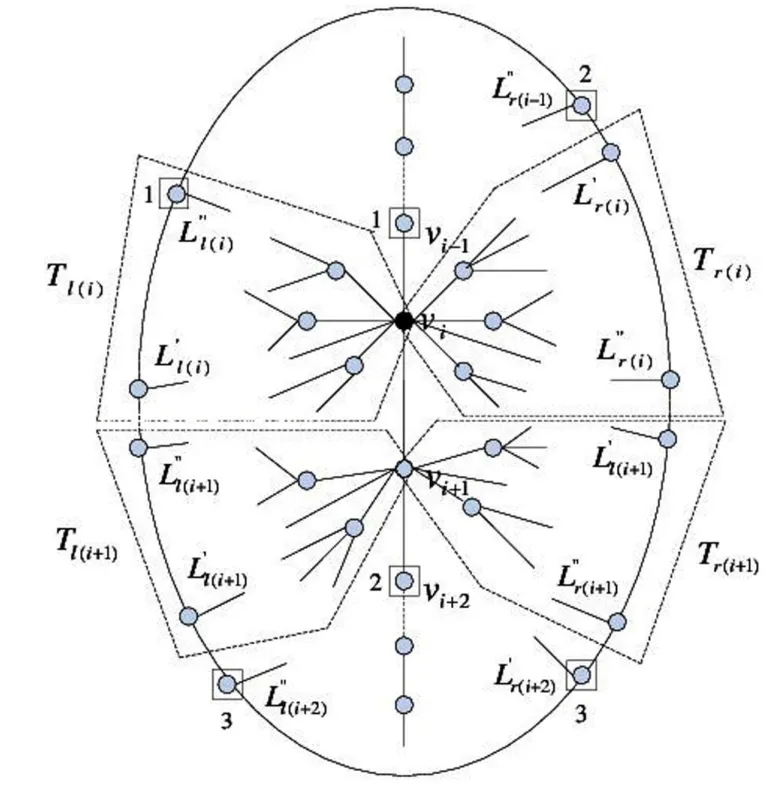
图 1 路 P上顶点 vi处起火时的防火策略

易见:当火在 v1处燃起时,采用策略 1)能救下 T-V(T1)中的所有顶点,即 sn2(v1)≥n-t1;当火在vk处燃起时,采用策略 2)能救下 T-V(Tk)中的所有顶点,即 sn2(vk)≥n-tk;当火在 vi处燃起时 (2≤i≤k-1),采用策略 3)能救下 T-V(Ti)-V(Ti+1)中的所有顶点,即 sn2(vi)≥n-ti-ti+1.因此
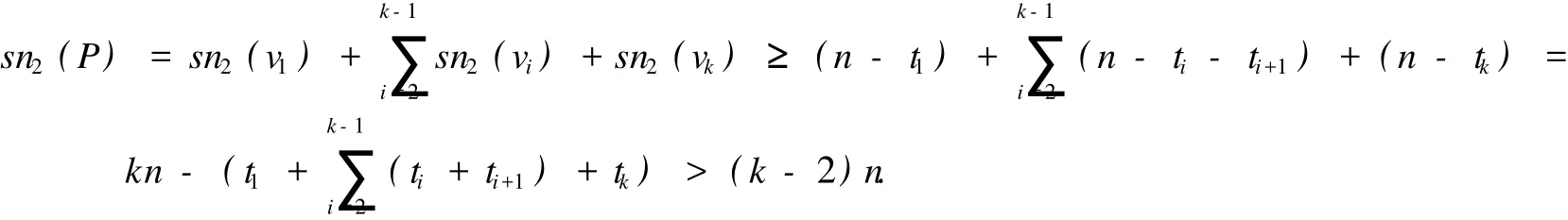
引理 1证毕.
设 T是一个哈林图的特征树,Tr表示 T中以 r为根的子树.对每个点 v∈V(T),存在唯一一条 (r,v)-路 rx1x2…xkv,称 xk为 v的父亲,而 v的其他邻点称为 v的儿子.一个有根树 Tr的高度定义为它的从根到叶子的最长路的长度;一个顶点 v在 Tr中的高度定义为有根子树 Tv的高度.

图 2 有根子树的防火策略
引理 2 设 H=T∪C是一个哈林图,S是 T中高度为 h的有根子树,那么 sn2(S)≥(n-h)|S|.
证明 任取 v∈V(S).设 Tv是 T的以 v为根的子树,C=y0y1…ym-1y0是 H的外圈,且定义 C的方向是顺时针的.于是,存在 C中的一段路 Q=yiyi+1…yj,使得 V(Q)是 Tv的所有叶子的集合,其中下标取模 m.
假设火在 v处燃起,则执行下面的防护策略 (如图2所示):
第 1步:防护 yj和 v在 T中的父亲 v′;
第 2步:防护 yi-1.
易见,应用上面的策略,可以救下 yi-1和 T-V(Tv)中的所有顶点 (注意 Tv=Sv).如果 S=T且火源在根部,那么就能防护根的儿子节点.
设 Hi(0≤i≤h)是 S中高度为 i的顶点集合,那么对任意示 Tv的顶点个数.因此

故
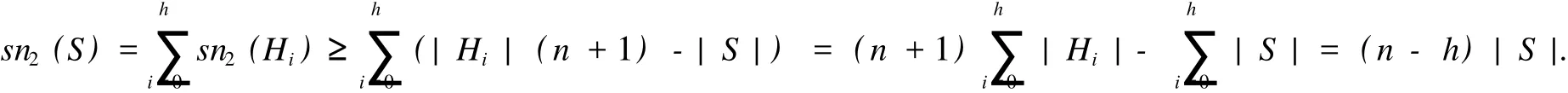
引理 2证毕.

证明 任选一个顶点作为 T的根,然后对 T的高度运用归纳法,证明 T可以被剖分成长路集合 P和短树集合 S的并.设 P是 T中一条从根到叶子的最长路.如果 P的顶点个数少于 2n,那么 T的高度至多为 2n-2.因此 T就是一棵短树,结论成立.否则,删去 T中所有 P的顶点得到一个森林 F.F是有根树的集合,且 P的选择保证了 F中的每棵有根子树也是 T的有根子树.另外,F的每棵子树的高度小于它在 T中的高度.由归纳假设,F中的每棵子树可以被剖分成长路集合和短树集合.这些集合和 P就可以满足对 T的剖分要求.
如果 T本身是一棵短树,即 P=Ø,结论可以由引理 2直接得到.否则假设 |P|≥1,由引理 1和引理2得
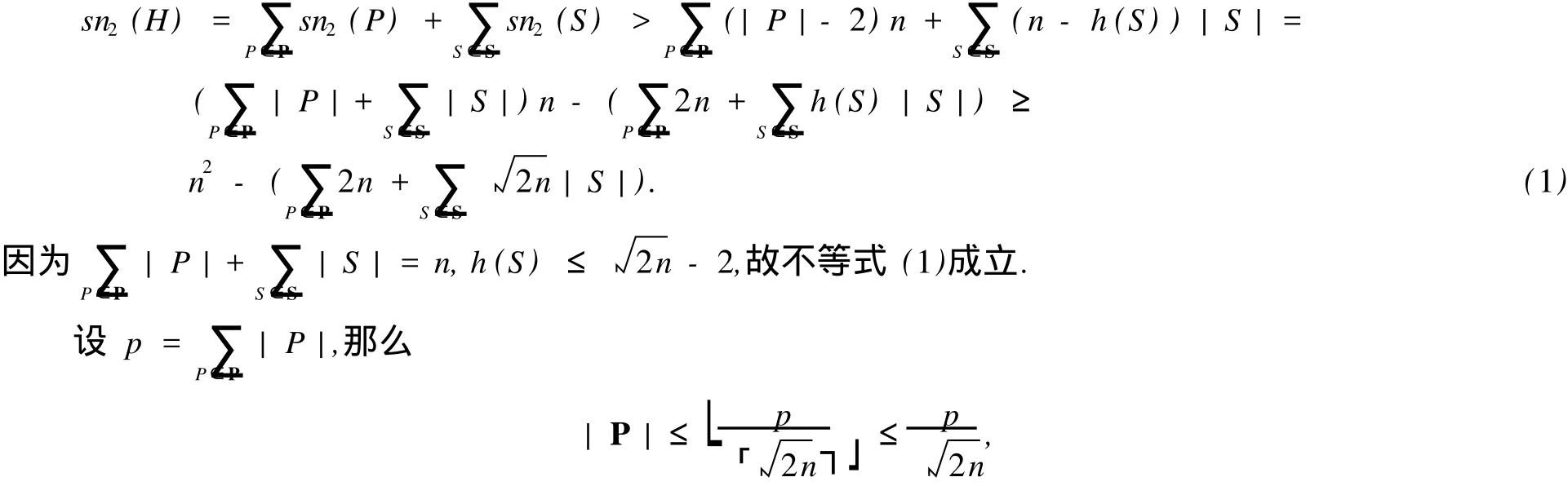
故

因此
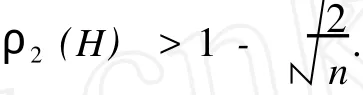
定理 1证毕.
由定理 1立即得到推论 1.
[1]CaiLeizhen,WangWeifan.The surviving rate of a graph for the firefighter problem[J].SI AM J DiscreteMath,2009,23(4):1814-1826.
[2]WangWeifan,Finbow S,Wang Ping.The surviving rate of an infected network[J].Theoretical Computer Science,2010,411(40/41/42):3651-3660.
[3]Finbow S,King A,MacGillivraya G,et al.The firefighter problem for graphs of maximum degree three[J].Discrete Math,2007,307(16):2094-2105.
[4]Wang Ping,Moeller SA.Fire control on graphs[J].J CombMath Comb Comp,2002,41:19-34.
[5]Finbow S,HartnellB,LiQ.On minimizing the effects of fire or a virus on a network[J].J CombMath Comb Comp,2000,33:311-322.
[6]ChanW H,PeterC B Lam,ShiuW C.Edge-face total chromatic numberof Halin graphs[J].SI AM J DiscreteMath,2009,23(3):1646-1654.
[7]ChenMin,WangWeifan.The 2-dipath chromatic number of Halin graphs[J].Inform ProcessLett,2006,99(2):47-53.
[8]Stadler P F.Minimum cycle bases of Halin graphs[J].J Graph Theory,2003,43(2):150-155.

