一类热传导方程逆时反问题的数值解法*
葛美宝, 徐定华
(1.浙江理工大学科技与艺术学院,浙江杭州 311121;2.浙江理工大学理学院,浙江杭州 310018)
0 引言
大量热传导方程的逆时反问题(BHCP)以不同的形式出现在热传导、流体学、材料学及工程科学的实际应用中.热传导方程反问题有着重要的应用价值,但也存在严重的不适定性,这种不适定性表现在解有可能不存在,即使存在也可能不稳定,即测量数据的微小变化将引起解的急剧变化,从而导致数值处理的极端困难.因此,这类反问题的研究吸引了国内外众多学者的关注,同时得到了一些好的正则化方法和误差估计[1-9].如:Latter和 Lion[1],Showalter[2]及 Ames等[3]利用拟逆法求解 BHCP 的数值解;熊向团等[4]利用中心差分法和拟逆法求解了一类不含源项的热传导方程反问题的数值解,得出了解的稳定性估计;Denisov[5]讨论了在三维空间中含有自伴椭圆算子抛物型方程的反问题,通过拟解法进行数值模拟,同时给出了正问题解的稳定性估计和拟解的存在性结果;葛美宝等[9]讨论了一类含源项ρ(t)u(x,t)的抛物型方程逆时反演的拟解法,并给出了正问题解的稳定性估计.本文利用文献[4]的中心差分算法求解了一类含源项q(x)u(x,t)的逆时反问题的数值解法,数值结果表明了中心差分方法的有效性和可行性.为了叙述简单起见,本文仅以一维区域为例.本文的方法可推广至更加广泛的反应扩散方程[10],考虑有界区间上的反问题,对二维情形同样适用.
热传导方程逆时反问题(BHCP):设 QT=[a,b]×[0,T],求初始分布函数

式(1)中:u(x,t)是下面问题的解:

D为热传导系数,q(x)为源项系数.
1 中心差分方法
本文利用文献[4]中的中心差分方法求解反问题(式(2)).利用中心差分代替uxx,得到方程如下:
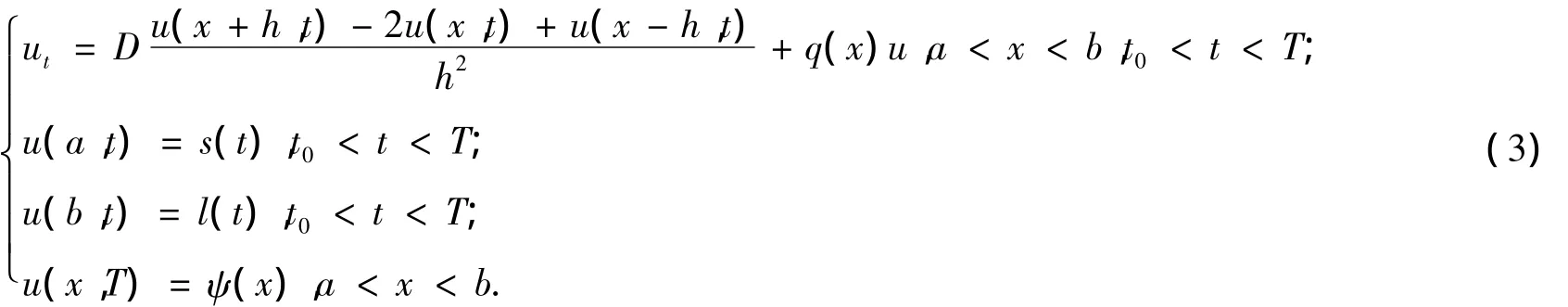
令 t^=T-t,w(x,t^)=u(x,t),则可得到
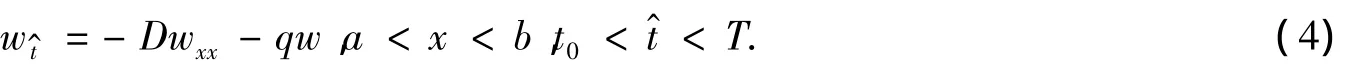
根据二阶中心差分,在xi处用差商代替微分wxx,则式(4)变形为

式(5)中:xi=a+(i-1)h,i=1,2,…,M+1;h=(b-a)/M;wi=wi(t^)=w((i-1)h,t^).则由方程式(3)中的边界条件可知:w1(t^)=l(t^),w2n+1(t^)=s(t^).此时方程(5)加上初始条件可得:
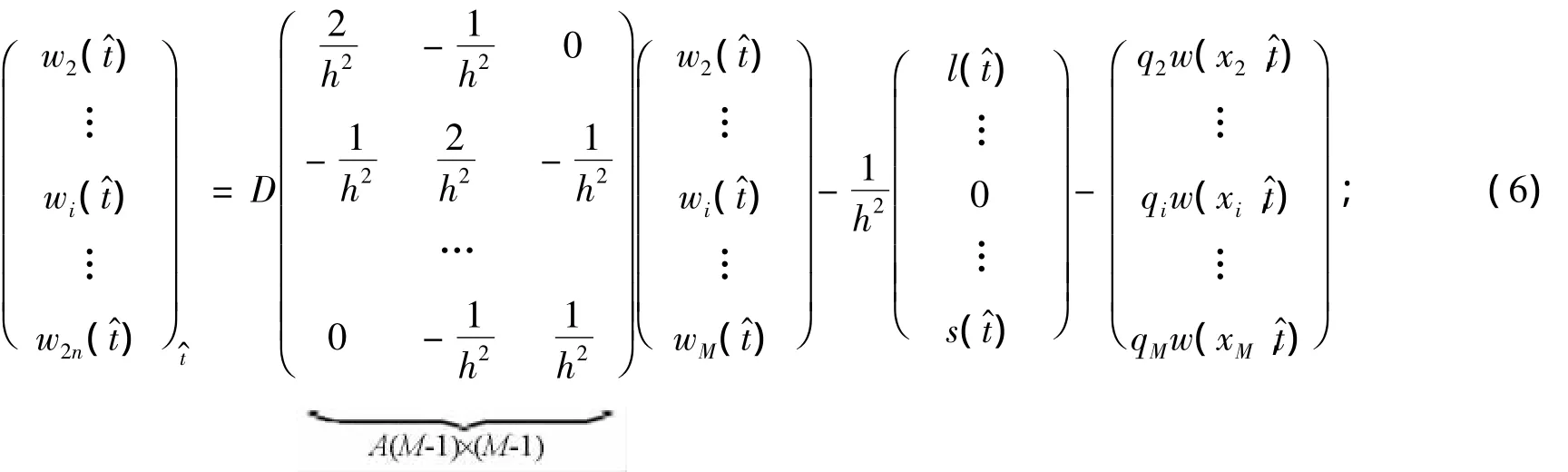
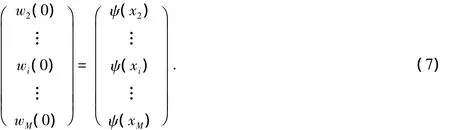
这是一个带有初始条件的非线性常微分方程组,对式(6)~式(7)的求解在数值计算上有很多方法,如欧拉法、龙格库塔方法和线性多步法等.但是根据矩阵A特征值的计算方法,上面的特征值
于是,现在做如下的变换:
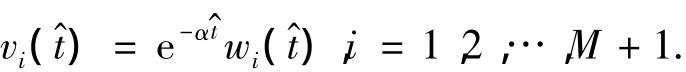
其中α>0为压缩因子.此时,式(5)变为
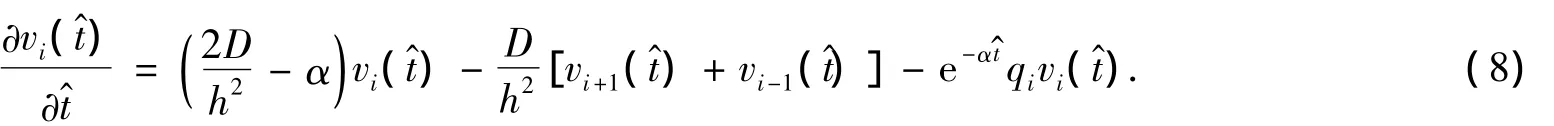
同理可以得到:

2 数值模拟
在这一部分中,笔者将运用中心差分法求解具体的实例,然后通过Matlab[11]上机进行数值模拟,从而说明该算法的有效性.
考虑下面的正问题:
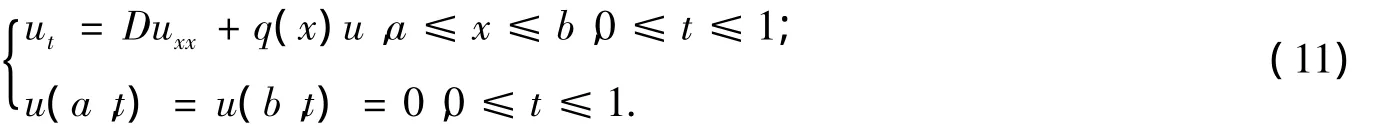

根据差分格式(12),可以计算出2种情形中u(x,T)的数值,结果如图1所示.
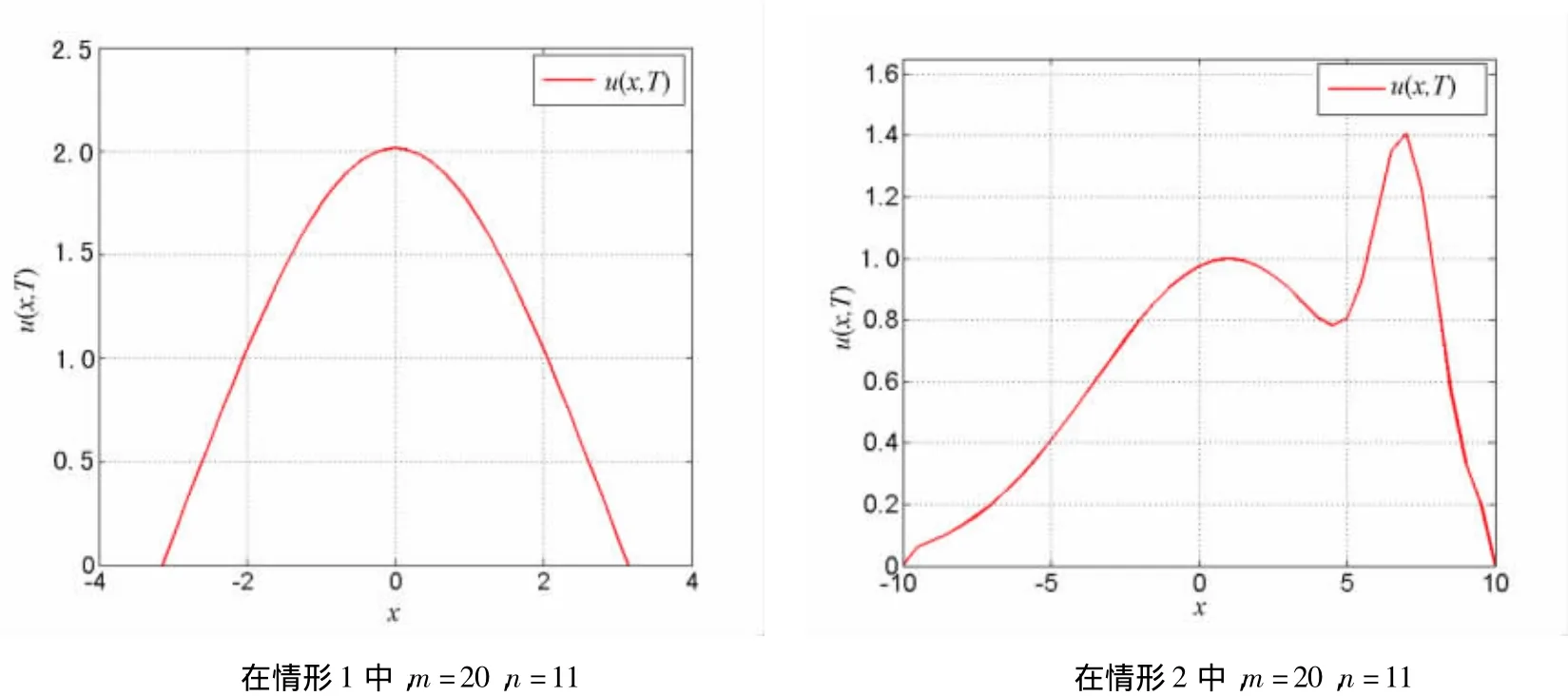
图1 由式(12)计算得到u(x,T)的数值解
根据上述反问题的求解算法,利用图1中已经计算的数值解u(x,T)=ψ(x),反求u(x,0)的数值解,结果见图2(情形1)和图3(情形2).
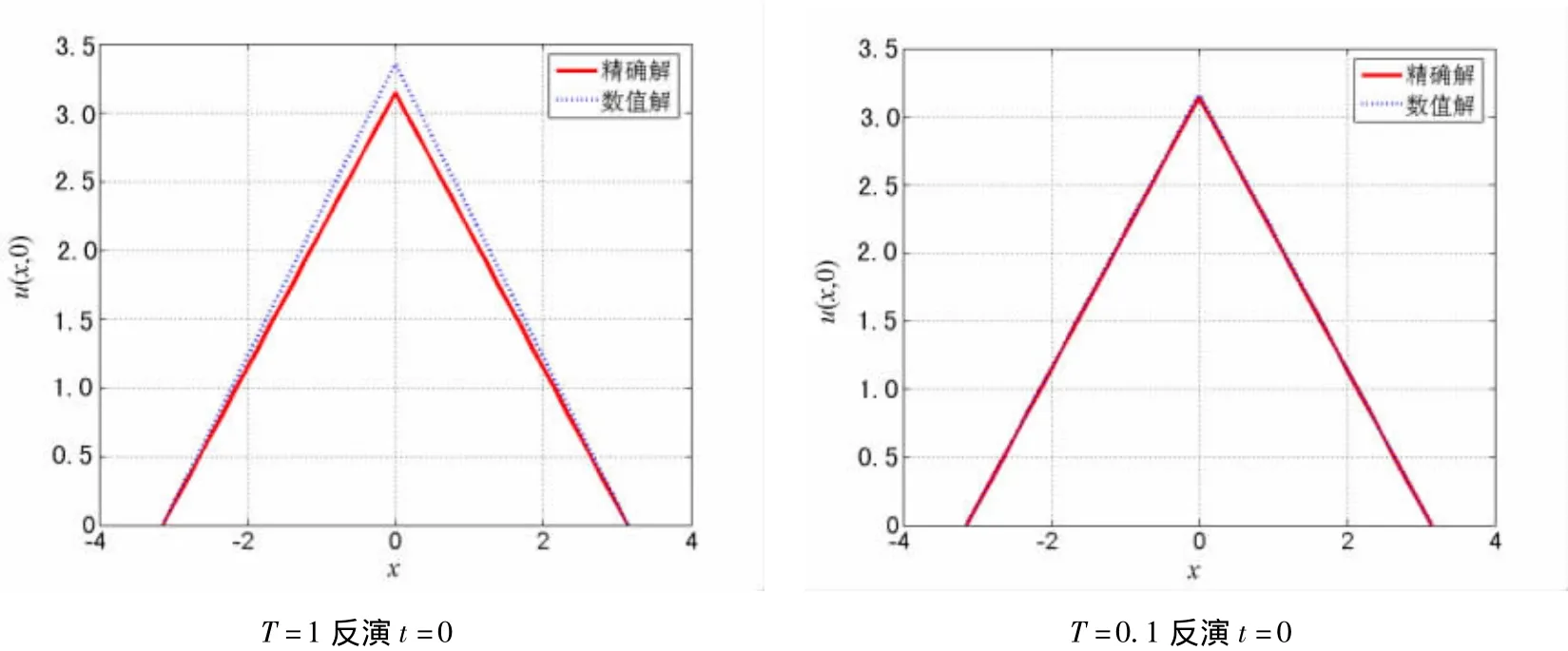
图2 u(x,0)数值解与精确解的比较,β =3,m=20,n=11(情形1)
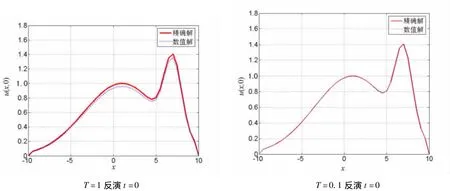
图3 u(x,0)数值解与精确解的比较,β =3,m=5,n=10(情形2)
3 结论
利用中心差分法求解了一类含源项q(x)u(x,t)的热传导方程逆时反问题.当T,M,N,b取不同值时,对精确解和数值解进行数值模拟,结果表明:
1)反问题的稳定性依赖于终止时间,随着终止时间T的增加,反问题的稳定性逐渐降低;反演的时间间隔越长,结果的精确度越低.
2)利用该方法求解热传导方程逆时反问题具有稳定性好、精度高的特点,值得在实际应用中采用,而且这种方法也可推广到高维的情形.
3)反问题的结果与正则化参数β的选取有很大关系,一般要求β≥2.β值具体如何选取,还需要进一步的研究.
[1]Lattes R,Lions J L.The Method of Quasi-Reversibility,Applications to Partial Differential Equations[M].New York:Elsevier,1969.
[2]Showalter R E.The final value problem for evolution equations[J].J Math Anal Appl,1974,47(5):563-572.
[3]Ames K A,Gordon W C,Epperson J F.A comparison of regularizations for an ill-posed problem[J].Math Comput,1998,67(12):1451-1471.
[4]Xiong Xiangtuan,Fu Chuli,Qian Zhi.Two numerical methods for solving a backward heat conduction problem[J].Math Comput,2006,179(9):370-377.
[5]Denisov A M.Element of the theory of inverse problem[M].Utrecht:VSP BV,1999.
[6]Hasanov A,Mueller J L.An umerical method for backward parabolic with non-selfadjoint elliptic operators[J].Applied Numerical Mathematics,2001,37(13):55-58.
[7]Elden L.Time discretization in the backward solution of parabolic equation[J].Math Comp,1982,39(11):53-68.
[8]刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005.
[9]葛美宝,徐定华,王泽文,等.一类抛物型方程反问题的数值解法[J].东华理工大学学报,2006,29(3):284-288.
[10]叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1999.
[11]张志涌.精通MATLAB5[M].3版.北京:北京航空航天大学出版社,2000.
[12]孙志忠.偏微分方程数值解法[M].北京:科学出版社,2005.

